基于改進粒子群算法的移動機器人多目標點路徑規劃

蒲興成，李俊杰，吳慧超，張毅

(1.重慶郵電大學 數理學院，重慶 400065；2.重慶郵電大學 智能系統及機器人研究所，重慶 400065；3.重慶郵電大學 先進制造學院，重慶 400065)

基于改進粒子群算法的移動機器人多目標點路徑規劃

蒲興成1，李俊杰2，吳慧超2，張毅3

(1.重慶郵電大學 數理學院，重慶 400065；2.重慶郵電大學 智能系統及機器人研究所，重慶 400065；3.重慶郵電大學 先進制造學院，重慶 400065)

針對移動機器人遍歷多個目標點的路徑規劃問題，提出了一種基于改進粒子群算法和蟻群算法相結合的路徑規劃新方法。該方法將目標點的選擇轉化為旅行商問題，并利用蟻群算法進行優化，定義了每兩個目標點之間的路徑規劃目標函數，利用粒子群算法對其進行優化。針對粒子群算法存在的早熟現象，將反向學習策略引入粒子群算法，并對粒子群算法的慣性權重和學習因子進行改進。性能測試結果表明，改進的粒子群算法能有效避免粒子早熟現象，提高粒子群算法的尋優能力及穩定性。仿真實驗結果驗證了新方法能有效地實現機器人的多目標點無碰撞路徑規劃。真實環境下的實驗結果證明了新方法在機器人多目標點路徑規劃的實際應用中也具有有效性。

移動機器人；多目標點路徑規劃；蟻群算法；改進粒子群算法；反向學習策略；慣性權重；學習因子

中文引用格式：蒲興成，李俊杰，吳慧超，等.基于改進粒子群算法的移動機器人多目標點路徑規劃[J]. 智能系統學報， 2017, 12(3): 301-309.

英文引用格式：PU Xingcheng， LI Junjie， WU Huichao, et al. Mobile robot multi-goal path planning using improved particle swarm optimization[J]. CAAI transactions on intelligent systems, 2017, 12(3): 301-309.

路徑規劃是研究移動機器人的一個重要內容，按其規劃范圍，分為全局路徑規劃和局部路徑規劃。目前，針對這兩種路徑規劃方式許多學者進行了深入研究，并提出了相應的解決方法。全局路徑規劃方法有柵格法、可視圖法和神經網絡法等；局部路徑規劃方法包括人工勢場法、A*算法、人工蜂群算法等[1]。雖然這些算法得到廣泛應用，但也存在一些缺點：柵格力度越小，柵格法對障礙物的描述越精確，但環境信息的存儲會占據大量的存儲空間，算法的搜索范圍也將成指數增加[2]；人工勢場法由于斥力的作用，機器人很難準確到達目標點。A*算法對開放列表的維護是最耗時的，尤其是在地圖過大的情況下。

移動機器人多目標點路徑規劃是指在復雜的環境下找到一條從起始點開始經過所有目標點的無碰撞的最優路徑。在實際應用中，移動機器人多目標點路徑規劃多應用于電廠巡檢、醫院查房等。移動機器人多目標點路徑規劃的基本原則包括3個方面：1)當前點或起始點以及目標點提前已知；2)任意時刻機器人都可以決定移動路線；3)機器人必須經過的所有目標點來完成路徑規劃。根據移動機器人多目標點路徑規劃的特點，移動機器人多目標點路徑規劃問題可以轉化為旅行商(traveling saleman problem, TSP)問題。目前有很多算法用于解決TSP問題[3]，但多目標點路徑規劃與TSP問題相比更復雜。因此本文提出了一種基于粒子群算法和蟻群算法相結合的混合算法用于解決移動機器人多目標點路徑規劃問題。

蟻群算法(ant colony optimization, ACO)是一種啟發式進化算法，由螞蟻覓食行為演化而來。在解決TSP問題上，蟻群算法表現出了較強的優越性。粒子群算法(particle swarm optimization, PSO)是一種群體智能算法，由鳥群覓食行為演化而來[4]。與一般的群體智能算法相比，PSO具有記憶特性，可以通過自我學習和向他人學習方式獲得更多的信息。由于參數少，計算方便等優點，PSO廣泛應用在優化問題上，并取得了很好的效果。隨著移動機器人技術的發展，國內外學者對粒子群算法在移動機器人路徑規劃上做了大量的研究，如多機器人路徑規劃[5-6]，自由浮動機器人軌跡規劃[7]以及其他應用領域[8-9]。PSO在路徑規劃上應用廣泛，ACO善于解決TSP問題，因此采用兩者結合的方式非常適合移動機器人多目標點路徑規劃問題。

在一個包含障礙物的空間內，利用PSO算法對起始點到目標點及每個目標點與目標點之間進行路徑規劃。起始點、目標點以及障礙物位置已知，但是哪一條路線會被選擇是未知的。為了確定哪一條路徑會被選擇，ACO被用于遍歷起始點和所有目標點，以便得到一條經過所有點的最短路徑。為了避免PSO出現早熟現象，提高算法的效率，提出了具有快速收斂性的粒子群算法。實驗結果驗證了混合算法的有效性以及改進的粒子群算法的優越性。

1 問題描述

1.1 多目標點路徑規劃

假設在移動機器人多目標點路徑規劃中含有n個目標點，則移動機器人會產生n(n-1)/2條路徑。為了滿足移動機器人行走路徑最短的要求，機器人需要從n(n-1)/2條路線中選擇出一條經過所有點的最短路徑。圖1描述了在起始點和目標點位置已知的情況下，移動機器人的運動軌跡。從圖1(a)中可知移動機器人的移動路線有很多條，且必須經過所有目標點才能完成路徑規劃；圖1(b)表示移動機器人運動的理想路線。

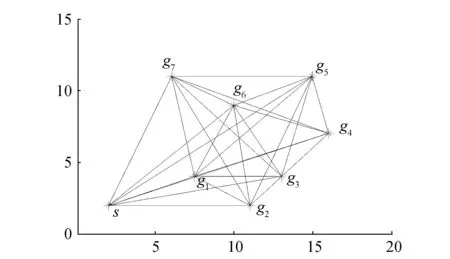
(a)所有路徑

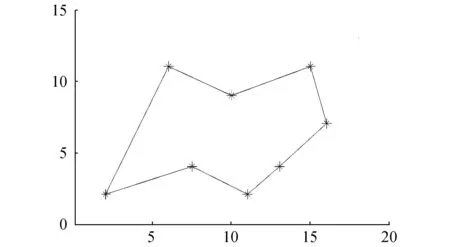
(b)理想路徑圖1 多點之間的路徑軌跡Fig.1 The path trajectory of multi-goal

為了解決上述問題，我們將目標點的選擇規劃為TSP問題的一個分支。目前，求解TSP問題最有效的方法主要有郭濤算法、模擬退火算法、遺傳算法、蟻群算法等[3]。由于這些算法都有優缺點，因此有些學者嘗試結合兩種或多種算法解決彼此算法上的缺點[10]。蟻群算法作為一種自組織正反饋算法，與其他算法相比，具有很強的魯棒性。而且從本質上講，蟻群算法的并行特性，強化了算法的可靠性。因此在解決多目標點選擇的問題上，我們將采用蟻群算法搜索能夠遍歷所有目標點的方法。

1.2 粒子的適應度函數

粒子的適應度函數是檢驗粒子群算法收斂性的重要函數。在路徑規劃中，移動距離最短是機器人首要考慮的目標，其次是安全性。因此，將移動機器人運動距離作為粒子的首要適應度函數。移動機器人多目標點路徑規劃如圖2所示。由圖2可知，移動機器人從起始位置開始避開障礙物，經過一系列目標點到達目標點n。

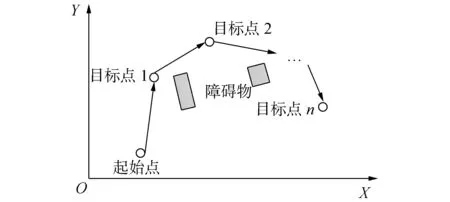
圖2 移動機器人多目標點路徑規劃示意圖Fig.2 The diagram of mobile robot multi-goal path planning

為了便于理解移動機器人多目標點路徑規劃，可將圖2中的多目標點路徑規劃分解為多個目標點中的兩兩目標點之間路徑規劃。機器人在保證兩點之間路徑規劃最短的基礎上才能保證多目標路徑規劃最短。分解后如圖3所示，機器人在當前點需要選擇下一個所經過點，然后到達目標點，在此期間要避開障礙物。

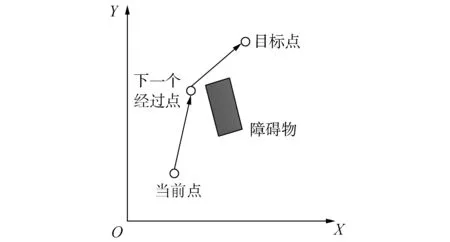
圖3 當前點到目標點避障描述 Fig.3 The obstacle avoidance description of current point to goal

綜上所述，為了保證路徑規劃的最短性，下一個移動點的選取是保證移動機器人運動軌跡最短的前提。因此，設立移動機器人路徑規劃目標函數F1，F1決定了移動機器人行走路徑長度。本文中，F1定義為

式中，g是目標點的個數，S是粒子個數。

移動機器人在向目標點移動過程中，除了要保證其最短性，安全性也是必須要考慮的。為此，將障礙物對目標點的斥力場函數作為安全性的懲罰函數。斥力場函數定義如下：

式中：F2是障礙物對機器人的斥力；kr是斥力場系數；d(xR,xO)為機器人到障礙物的距離；d(xR,xG)是機器人到目標點的距離；dm是障礙物的影響范圍。

移動機器人多目標點路徑規劃問題可以抽象為當前位置到目標點的最短距離的優化問題，而障礙物對機器人的斥力作用是保證最短路徑安全性的前提。因此，針對路徑規劃的目標函數可以定義為

F=λF1+μF2

式中λ和μ分別是最短路路徑和約束條件的權重。

2 基本知識

2.1 標準粒子群算法

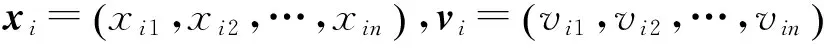
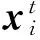
2.2 反向學習策略

Tizhoosh[11]在2005年基于相反數或對立點的概念提出了反向學習策略。在隨后的發展中，該方法被應用于解決一些優化問題中[12-13]。反向坐標定義如下。

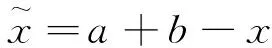
式中x∈[a,b]，且為實數。把上述定義應用到高維空間可表示成定義2。

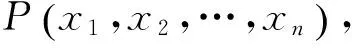
將定義2應用到優化過程中，則反向機制的優化過程如定義3。

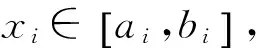
3 反向學習粒子群算法

基于反向學習策略的思想，本文提出一種改進的粒子群算法(opposition-based learning improved PSO, OBLIPSO)。本文采用反向學習策略時，將反向學習策略應用到單個粒子中，而不是粒子群體中，以便減小粒子迭代過程中的計算量。性能測試結果證明，改進的粒子群算法能抑制粒子早熟現象，提高收斂效率。下面介紹改進算法的主要機制和流程。

3.1 初始化種群

粒子在問題空間中找到最優解的時間與粒子初始化時在空間中的分布存在正比關系，距離最佳位置近的粒子找到最優解的時間比距離最佳位置遠的粒子要快。但是，粒子在問題空間中是隨機分布的，每一個粒子相對于最優解的位置都是未知的。

基于以上分析，在改進的粒子群算法初始化時引入反向學習策略有助于粒子尋找最優解。在初始化時，首先，計算粒子的適應度值以及其反向粒子適應度值，并對兩者進行比較，選擇適應度值較好的粒子；其次，從種群中選擇S個適應度值最好的粒子作為初始種群。

3.2 迭代進化過程

在標準PSO算法中，粒子在問題空間中選擇另一個粒子作為學習對象，根據式(1)、(2)進行移動。但在粒子進化的過程中，粒子會發生早熟現象，導致算法無法得到最優解。由式(1)可知，粒子的速度受到慣性權重和學習因子的影響：慣性權重影響著粒子的全局搜索和局部搜索能力，學習因子影響粒子獲取信息的能力。為了找到問題最優解，粒子在進化的過程中，其全局搜索能力和局部搜索能力也應該隨之發生變化，即從全局搜索漸變為局部搜索，保證粒子可以尋找到問題的最優解。同樣，粒子也應該逐漸增強社交能力，由“自我”學習逐漸向“他人”學習過渡，以便獲取更多有用的信息。

根據以上分析，粒子在尋優過程中，慣性權重應該保持動態變化。ω取值較大時，粒子的全局搜索能力較強；ω取值較小時，粒子的局部搜索能力較強。由于粒子在尋優的過程中，會逐漸靠近最優點，粒子的慣性權重應該隨著尋優過程自適應變化。因此粒子的慣性權重更新公式為

式中:ωmax和ωmin分別是粒子慣性權重的最大值和最小值;disti是第i個粒子到全局最優粒子的歐幾里德距離;max_dist是粒子到全局最優粒子的最大距離。disti和max_dist表達式分別為[15]

學習因子c1和c2控制粒子本身記憶與同伴記憶之間的相對影響：c1的值較小時，表現為自我認知能力不足；c2的值較小時，表現為社交能力不足。為了保證在迭代過程中，粒子的自我認知和社交能力能夠因時而異，因此，粒子的學習因子更新公式[16]如下：

式中：c1max和c2max以及c1min和c2min分別是學習因子c1和c2的最大值和最小值;t是當前的迭代次數；Tmax是最大迭代次數。

3.3 算法實現流程

1)首先初始化種群P(S)，包括粒子的位置xi和速度vi，i=1,2,…,S，S是種群的大小，初始化慣性權重ω以及學習因子c1和c2等參數。

2)在速度和位置規定的范圍內根據式(1)、(2)更新第i個粒子的速度vi和位置xi。

3)計算第i個粒子的適應度值fi。

4)ai=min(xi)。

5)bi=max(xi)。

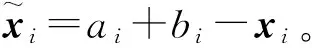
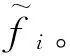
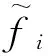
9)從最優適應度值中選出S個適應度值最好的粒子組成初始化種群。

10)接下來同粒子群算法基本流程。

11)算法滿足結束條件，結束算法過程。

4 實驗結果與分析

4.1 OBLIPSO性能測試

為了驗證改進粒子群算法的性能是否得到改進，筆者將反向學習的粒子群算法與其他改進算法[15，17-18]在4個適應度函數上進行對比。這4個適應度函數分別為Sphere函數、Rastrigin函數、Grewank函數、Schaffer函數，測試函數參數設置如表1所示。

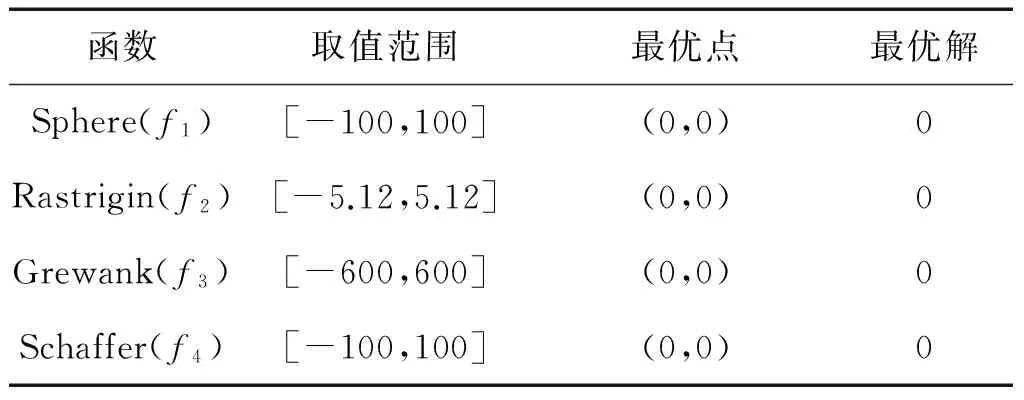
表1 測試函數參數設置

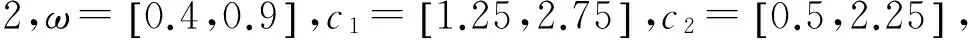
在表2中，OBLIPSO算法在四測試函數上的平均值均小于其他3種算法的值，尤其是在Sphere函數和Rastrigin函數中。從表2中數據可知，OBLIPSO算法具有更好的收斂性，得到的解更優。表3中的數據反映出改進算法的穩定性。OBLIPSO算法與IAPSO算法、IPSO算法和WPSO算法對比，在穩定性上表現得更好。

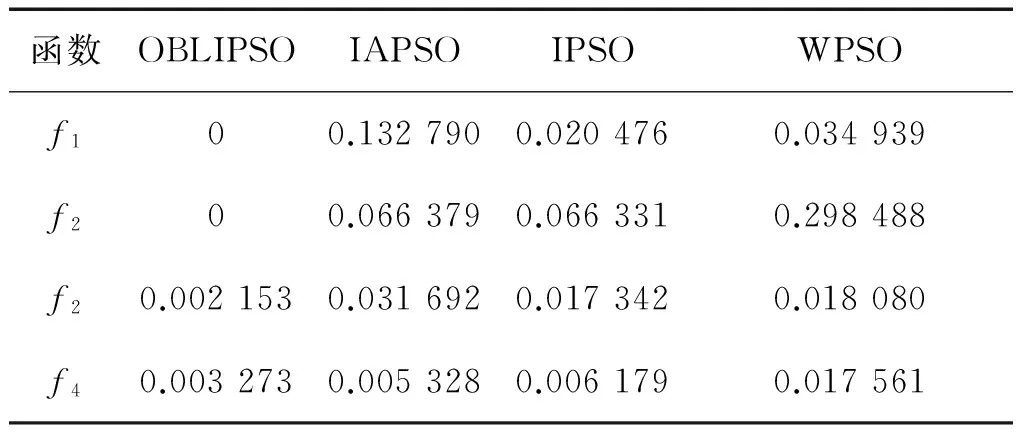
表2 平均最優值結果對比

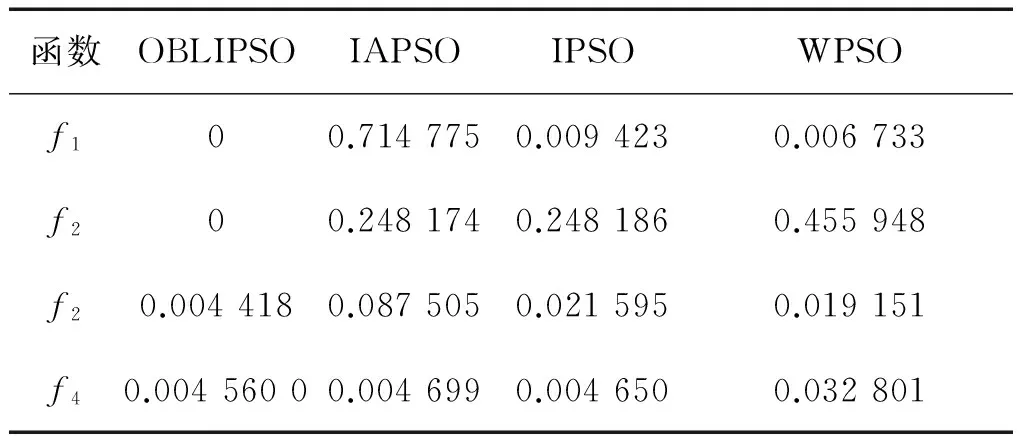
表3 標準方差結果對比

由表2和表3數據可得：反向學習策略提高了種群的多樣性，增加了粒子尋優成功概率，節省了粒子尋優時間；線性變化的慣性權重保障了粒子從全局搜索到局部搜索的線性轉換，抑制了粒子早熟現象；學習因子的變化保證了粒子能夠充分完成自我學習和社交行為，提高了粒子的收斂速度。

4.2 路徑規劃仿真實驗

為了驗證新方法的實用性及有效性，筆者將該方法在仿真環境下進行實驗。仿真實驗環境設置在18×16的二維矩形空間內，并設置成簡單環境和復雜環境。在環境中有不規則的障礙物，起始點位置使用方形表示，目標點處用五角形表示。

1) 第1次實驗中，OBLIPSO算法的參數設置為：ωmax=0.9，ωmin=0.4，S=10，c1max=2.75，c2max=2.25,c1min=1.25,c2min=0.5，vmax=1.9，vmin=0，斥力場中的安全距離dm=2，kr=2.7，λ=0.25，μ=0.25，最大迭代次數為100。圖4(a)給出了在簡單環境下的OBLIPSO作用的移動機器人多目標點移動軌跡。圖4(b)是IAPSO作用的運動軌跡。圖4(c)是IPSO作用的運動軌跡。

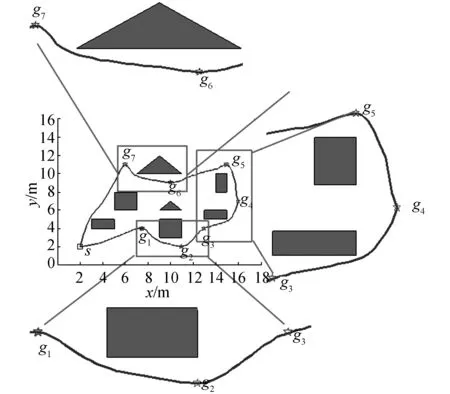
(a)OBLIPSO路徑軌跡

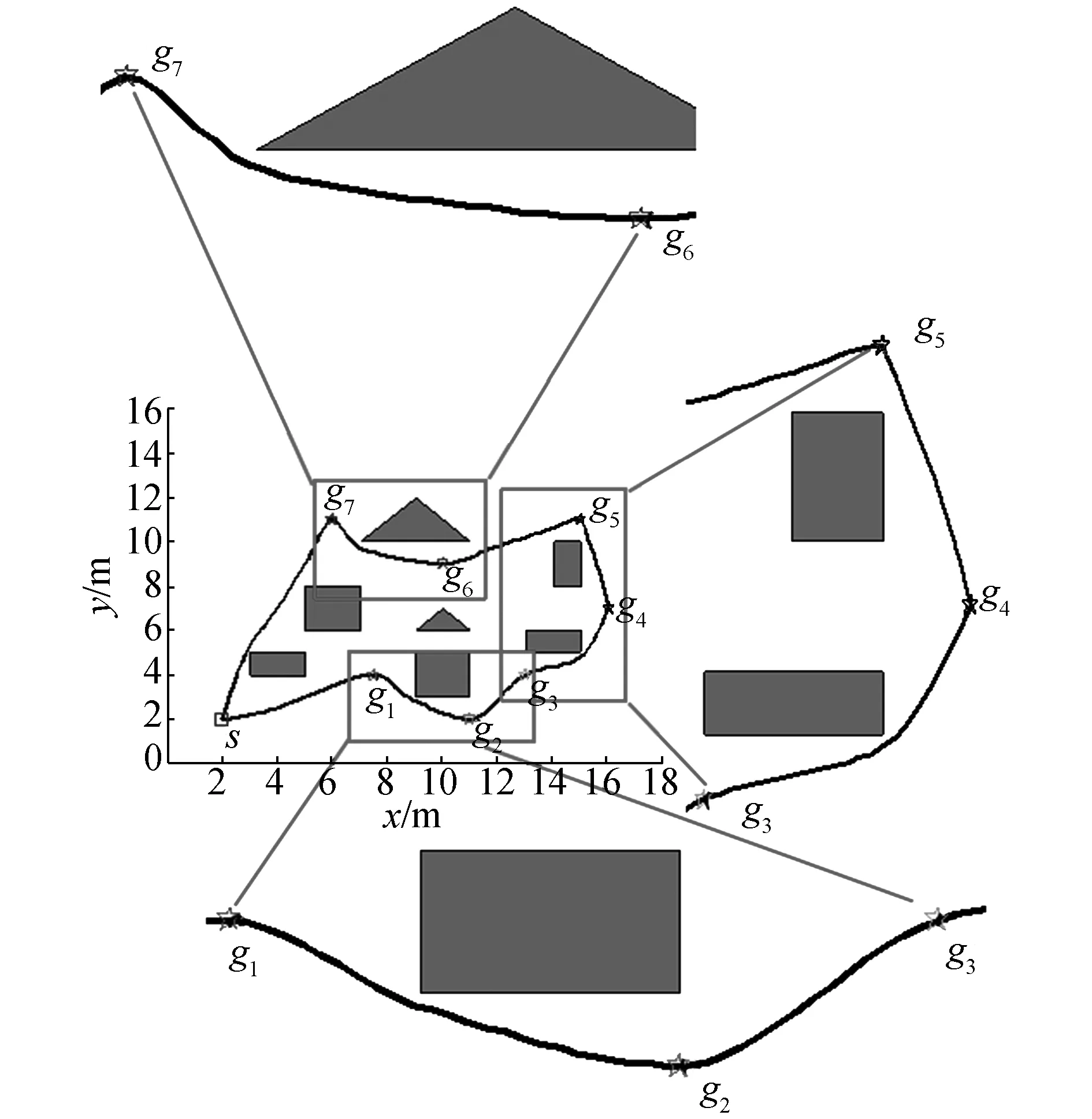
(b) IAPSO路徑軌跡

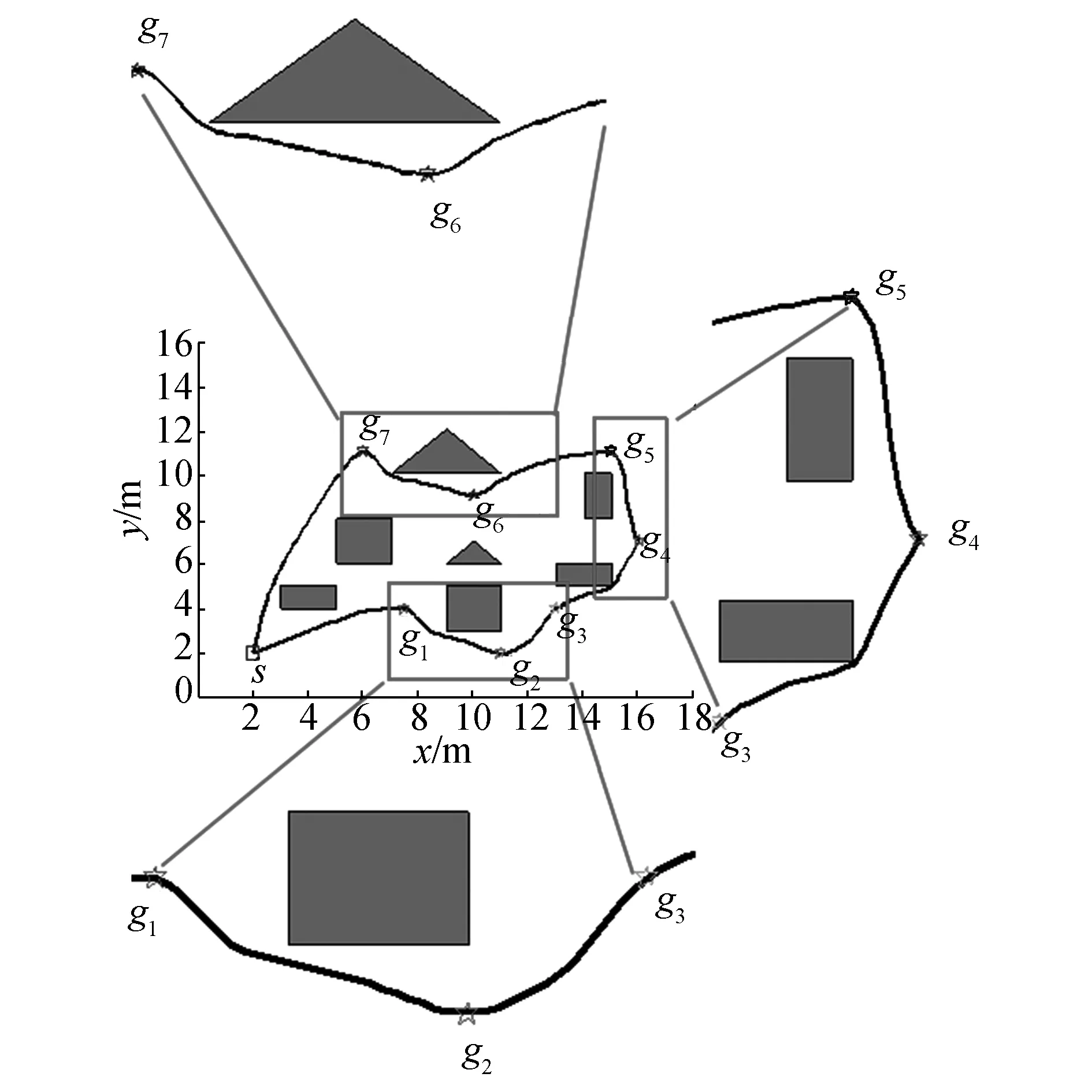
(c)IPSO路徑軌跡圖4 簡單環境下的優化過程Fig.4 The motion process in the first environment

由圖4框中路徑軌跡可知：在目標點3到目標點4和目標點6到目標點7之間，OBLIPSO和IAPSO的避障性能上優于IPSO，在經過目標點4和目標點5時，OBLIPSO的路徑較為平滑。而且OBLIPSO在迭代72次左右時成功完成路徑規劃。

2)在第2次實驗中，實驗環境相對第1次實驗而言，增加了障礙物以及目標點的個數。實驗參數設置如下：vmax=20，最大迭代次數為300，其余參數與第1次實驗中參數相同。由于環境復雜度的增加，相對第1次實驗而言，粒子收斂速度變慢。圖5(a)是在復雜環境下的OBLIPSO獲得的移動機器人多目標點運動軌跡。圖5(b)是IAPSO獲得的運動軌跡。圖5(c)是IPSO作用的運動軌跡。

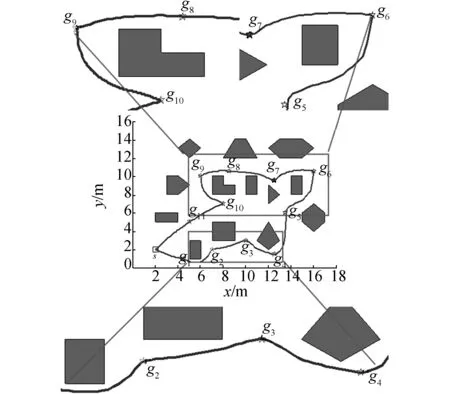
(a)OBLIPSO路徑軌跡

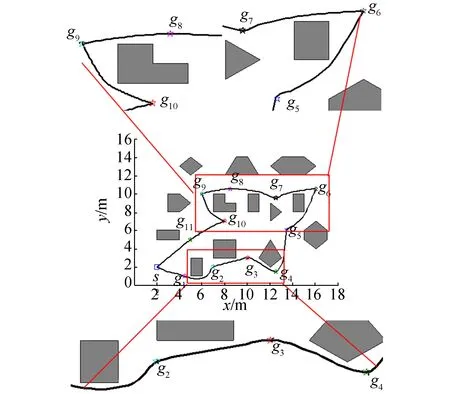
(b)IAPSO路徑軌跡

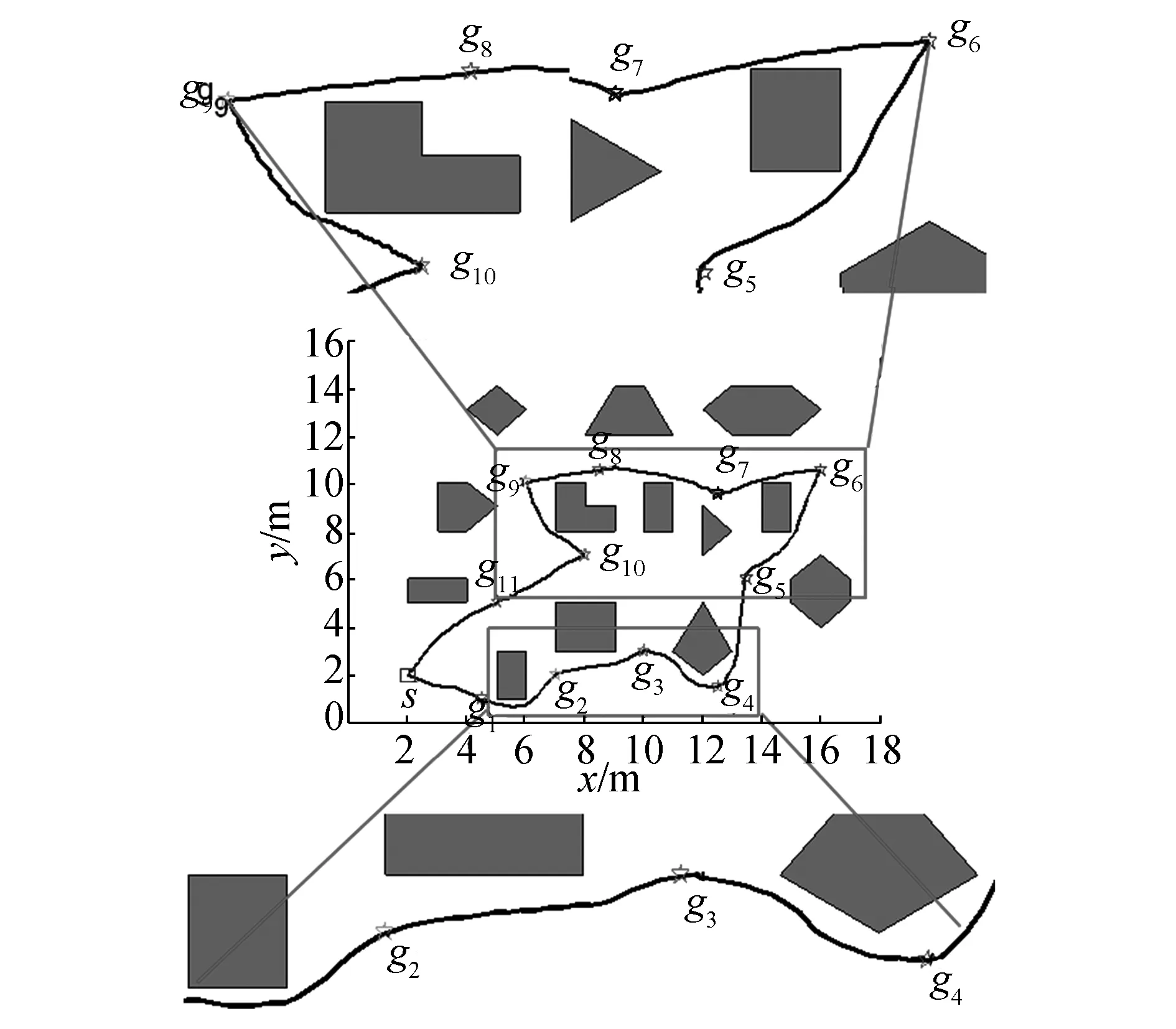
(c) IPSO路徑軌跡圖5 復雜環境下迭代過程Fig.5 The iteration process in complicated environment

對比圖5中3條軌跡可知，隨著障礙物和目標點增加，3種算法都滿足了路徑的可達性。根據圖5框中的路徑軌跡可知，在經過目標點6和目標點9時，OBLIPSO算法規劃的路徑相比于IAPSO和IPSO算法規劃的路徑更為平滑。OBLIPSO算法規劃的路徑在目標點5與目標點10之間相比于IAPSO和IPSO算法規劃的路徑安全性更好，OBLIPSO移動距離較短(見表4)，而且其規劃的路徑安全性最好。

3)路徑規劃性能對比

重復10次上述兩種任務的實驗，取其平均值。移動機器人多目標點路徑規劃的時間消耗和移動距離性能對比如表4所示。

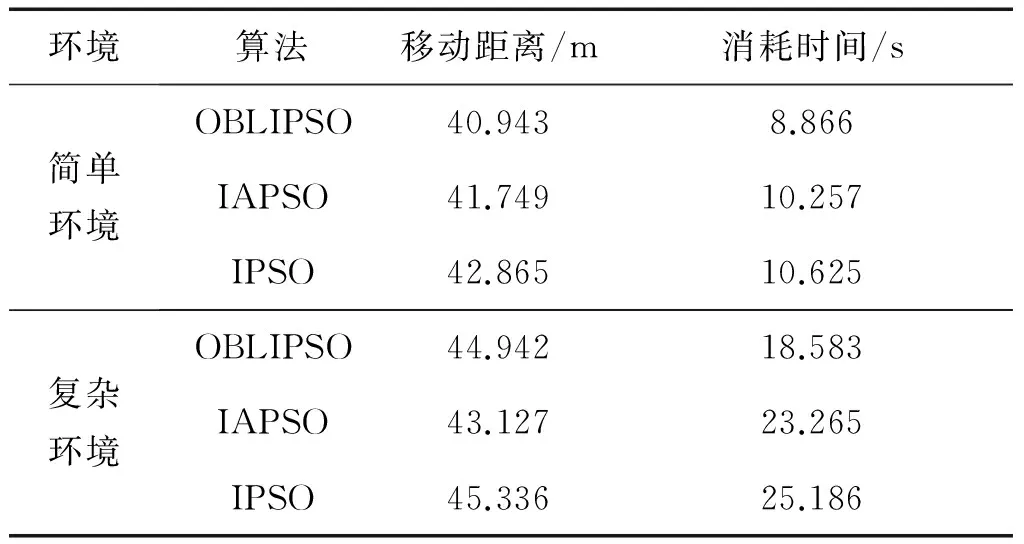
表4 路徑性能對比

從表4數據中可以得出，隨著任務復雜度的增加，OBLIPSO、IAPSO和IPSO在時間消耗上也在增加，任務越復雜，用時越多。但在進行相同任務時，OBLIPSO用時比IAPSO和IPSO少；在移動距離方面，簡單任務時，OBLIPSO的移動距離比其他兩種對比算法短，在復雜任務時，雖然OBLIPSO的移動距離長于IAPSO，但其比IPSO算法短；在路徑安全性方面，OBLIPSO算法要優于其他兩種對比算法。由于在設計路徑規劃目標函數時不僅考慮了路徑最短性問題，也考慮到了其安全性的問題，因此綜合兩種環境下實驗結果可以得出OBLIPSO算法綜合性能強于IAPSO算法和IPSO算法。

圖6給出的是簡單環境下OBLIPSO算法、IAPSO算法和IPSO算法在目標函數上的收斂曲線對比。從圖6中曲線可以得出，在迭代72次左右時，OBLIPSO算法可在多目標點路徑規劃中尋到最優路徑，而IAPSO算法和IPSO算法在迭代100次時仍未獲得OBLIPSO算法的收斂值。

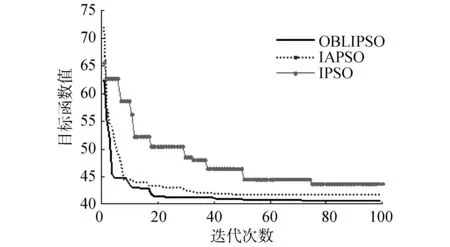
圖6 OBLIPSO與IAPSO和IPSO目標函數收斂曲線比較Fig.6 The convergence comparison of OBLIPSO with IAPSO and IPSO

綜上所述，在相同任務下，OBLIPSO算法的綜合性能優于IAPSO算法和IPSO算法。隨著任務復雜度的變化，OBLIPSO算法能夠有效且較好地完成移動距離和時間消耗以及安全性上表現得更好，表明了OBLIPSO算法能夠有效且較好地完成移動機器人多目標點路徑規劃上有效性。

4.3 實際環境下路徑規劃

為了驗證OBLIPSO算法在實際應用中的有效性，筆者將在實際環境下對OBLIPSO算法進行實驗驗證。實驗環境設置為重慶郵電大學自動化學院辦公樓一樓。實驗平臺為先鋒3機器人，軟件背景為ROS(robot operation system)[19-21]。實驗中設置了3個目標點，機器人從目標點1出發經過兩個目標點，最后返回目標點1。

圖7中顯示的是機器人在無障礙環境中完成的多目標點路徑規劃。圖7(a)為OBLIPSO算法規劃的路徑，圖7(b)為IAPSO算法規劃的路徑。由圖7可知：機器人從目標點2到目標點3的過程中，OBLIPSO算法能夠保證機器人與墻體保持安全距離且路徑平滑；IAPSO算法雖然保證了機器人與墻的安全距離，但由于機器人遠離墻體移動造成了路徑的交叉，如圖7中方框所示。

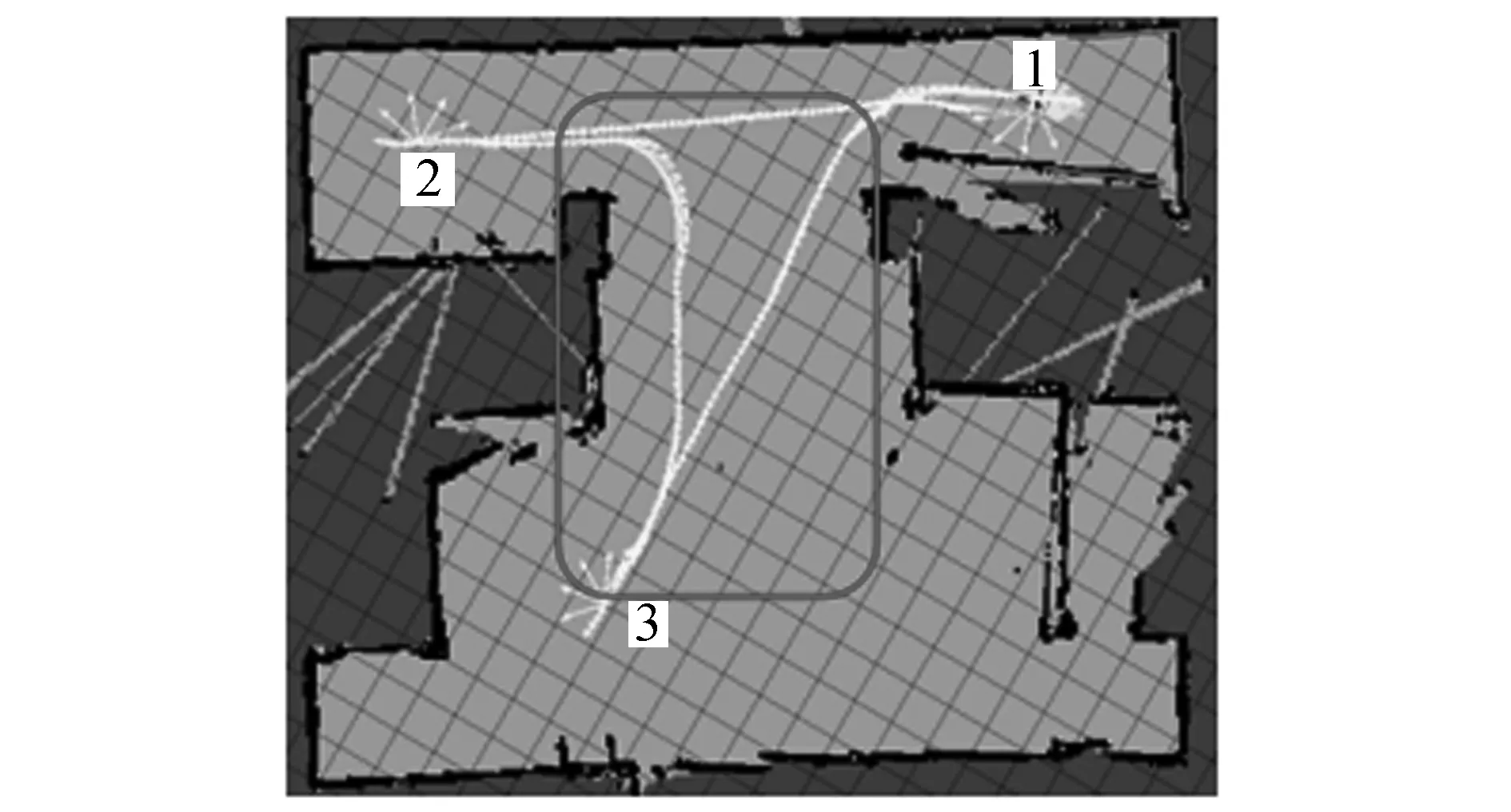
(a)OBLIPSO路徑軌跡

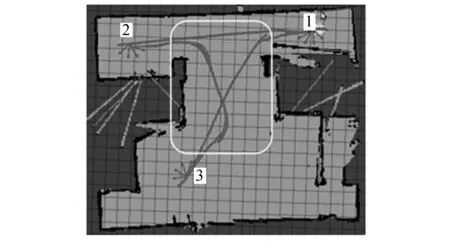
(b)IAPSO路徑軌跡圖7 機器人在無障礙環境下的移動過程Fig.7 The motion process of robot in barrier-free environment

為了進一步驗證OBLIPSO算法的有效性，環境中設置了障礙物，并改變了目標點3的位置，如圖8所示。圖8表示機器人在含有障礙物的環境下實現的多目標點路徑規劃。圖8(a)為OBLIPSO算法規劃的路徑，圖8(b)為IAPSO算法規劃的路徑。由圖8可知：在含有障礙物的環境中，機器人在兩種算法下都能夠避開障礙物完成路徑規劃，但是機器人從目標點2到目標點3的過程中，OBLIPSO算法能夠保證機器人與障礙物保持安全距離并且路徑平滑；IAPSO算法在移動過程中，雖然機器人與障礙物保持了安全的距離，但由于其路徑的交叉導致移動軌跡較長，如圖8中方框所示。

表5為兩次實驗重復10次取得的時間和路徑長度的平均值。由表5可知：在障礙環境下，OBLIPSO算法可以實現機器人多目標點的路徑規劃，并且消耗的時間較少。

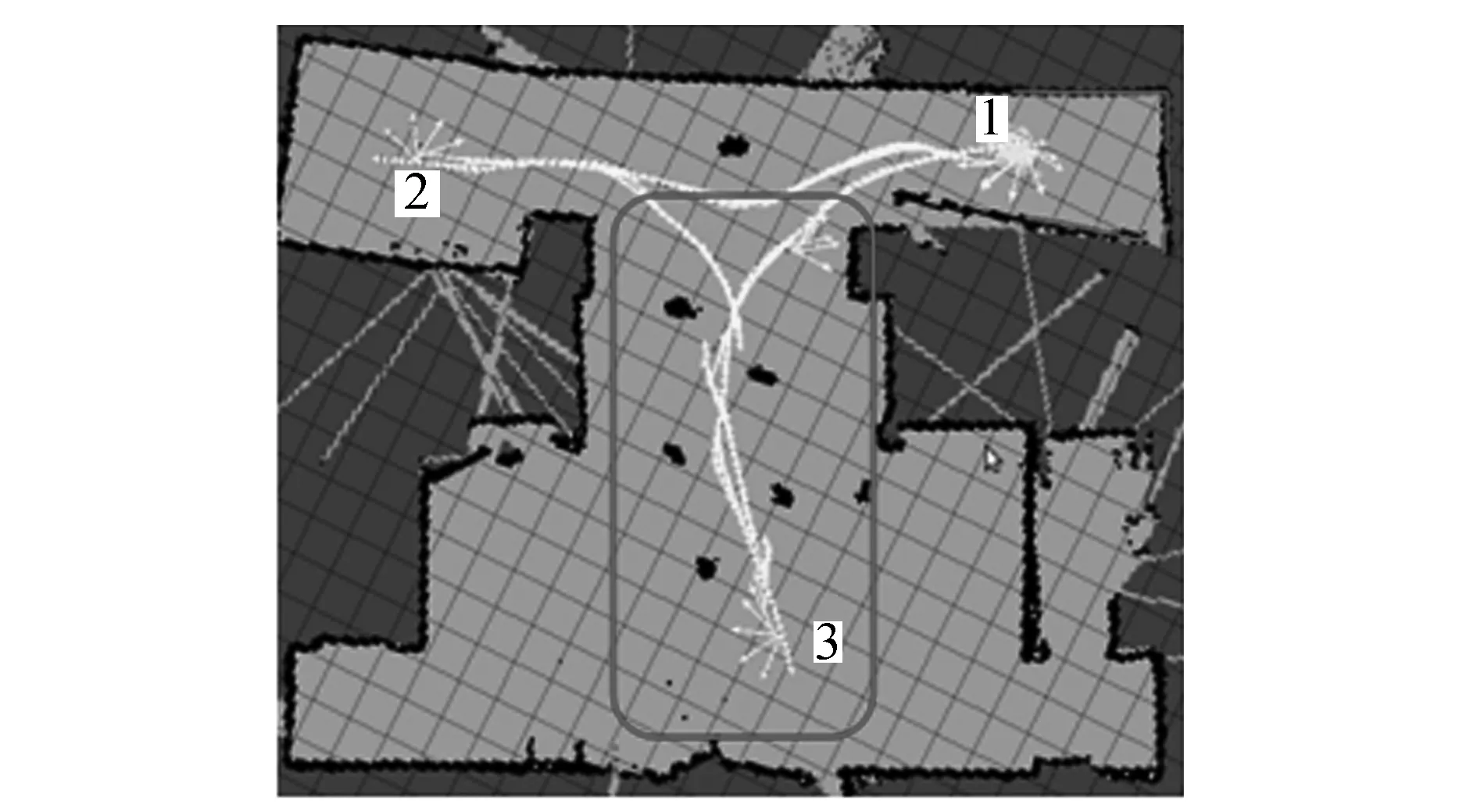
(a)OBLIPSO路徑軌跡

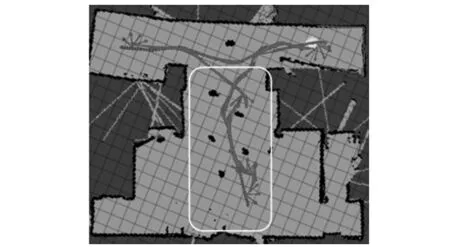
(b)IAPSO路徑軌跡圖8 機器人在障礙環境下的移動過程Fig.8 The motion process of robot in the obstacle environment

指標無障礙有障礙(OBLIPSO/IAPSO)(OBLIPSO/IAPSO)時間/s114/114186/216距離/m20.1/20.119.5/20

5 結束語

本文提出了一種結合ACO算法和OBLIPSO算法的移動機器人多目標點路徑規劃新方法，并通過實驗驗證了新方法的可行性。ACO算法在TSP問題上表現出較好的優越性，因此ACO算法適用于移動機器人的目標點選擇問題。OBLIPSO算法不僅繼承了PSO算法計算簡單的特點，而且在初始化時引入反向學習策略，保證了粒子的多樣性。在迭代過程中，OBLIPSO算法抑制了粒子的早熟，提高了收斂速度。采用4個適應度函數對OBLIPSO算法進行性能評估，取得了良好的測試結果。仿真實驗與真實環境下實驗結果表明提出的新方法是一種有效的多目標點路徑規劃方法。將本文提出的新方法應用到動態環境下的移動機器人的多目標點路徑規劃是下一步的研究內容。

[1]楊興, 張亞, 楊巍,等. 室內移動機器人路徑規劃研究[J]. 科學技術與工程, 2016, 16(15):234-238. YANG Xing, ZHANG Ya, YANG Wei, et al.Research on path planning of indoor mobile robot [J]. Science technology and engineering, 2016, 16 (15): 234-238.

[2]Ammar A, Bennaceur H, Chari I, et al. Relaxed Dijkstra and A*with linear complexity for robot path planning problems in large-scale grid environments[J]. Soft computing, 2016, 20(10):4149-4171.

[3]杜鵬楨, 唐振民, 孫研. 一種面向對象的多角色蟻群算法及其TSP問題求解[J]. 控制與決策, 2014(10):1729-1736. DU Pengzhen, TANG Zhenmin, SUN Yan. An object-oriented multi-role ant colony optimization algorithm for solving TSP problem[J].Control and decision, 2014 (10): 1729-1736.

[4]AGRAWAL R K, BAWANE N G. Multiobjective PSO based adaption of neural network topology for pixel classification in satellite imagery[J]. Applied soft computing, 2015, 28(C):217-225.

[5]DAS P K, BEHERA H S, PANIGRAHI B K. Intelligent-based multi-robot path planning inspired by improved classical Q-learning and improved particle swarm optimization with perturbed velocity[J]. Engineering science and technology, an international journal, 2015, 19(1): 651-669.

[6]YANG Mao, LI Chunzhe. Path planning and tracking for multi-robot system based on improved PSO algorithm[C]//Proceedings of 2011 International Conference on Mechatronic Science, Electric Engineering and Computer(MEC). Jilin: IEEE, 2011: 1667-1670.

[7]WANG Mingming, LUO Jianjun, WALTER U. Trajectory planning of free-floating space robot using particle swarm optimization(PSO)[J]. Acta astronautica, 2015, 112: 77-88.

[8]張萬緒, 張向蘭, 李瑩. 基于改進粒子群算法的智能機器人路徑規劃[J]. 計算機應用, 2014, 34(2): 510-513. ZHANG Wanxu, ZHANG Xianglan, LI Ying. Path planning for intelligent robots based on improved particle swarm optimization algorithm[J]. Journal of computer applications, 2014, 34(2): 510-513.

[9]王娟, 吳憲祥, 郭寶龍. 基于改進粒子群優化算法的移動機器人路徑規劃[J]. 計算機工程與應用, 2012, 48(15): 240-244. WANG Juan, WU Xianxiang, GUO Baolong. Robot path planning using improved particle swarm optimization[J]. Computer engineering and applications, 2012, 48(15): 240-244.

[10]張勇, 陳玲, 徐小龍, 等. 基于PSO-GA混合算法時間優化的旅行商問題研究[J]. 計算機應用研究, 2015, 32(12): 3613-3617. ZHANG Yong, CHEN Ling, XU Xiaolong, et al. Research on time optimal TSP based on hybrid PSO-GA[J]. Application research of computers, 2015, 32(12): 3613-3617.

[11]TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//Proceedings of 2005 and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, International Conference on Computational Intelligence for Modelling, Control and Automation. Vienna: IEEE, 2005: 695-701.

[13]汪慎文, 丁立新, 謝大同, 等. 應用反向學習策略的群搜索優化算法[J]. 計算機科學, 2012, 39(9): 183-187. WANG Shenwen, DING Lixin, XIE Datong, et al. Group search optimizer applying opposition-based learning[J]. Computer science, 2012, 39(9): 183-187.

[14]AL-QUNAIEER F S, TIZHOOSH H R, RAHNAMAYAN S. Opposition based computing-a survey[C]//Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN). Barcelona: IEEE, 2010.

[15]SURESH K, GHOSH S, KUNDU D, et al. Inertia-adaptive particle swarm optimizer for improved global search[C]//Proceedings of Eighth International Conference on Intelligent Systems Design and Applications. Kaohsiung: IEEE, 2008: 253-258.

[16]姜建國, 葉華, 劉慧敏, 等. 融合快速信息交流和局部搜索的粒子群算法[J]. 哈爾濱工程大學學報, 2015, 36(5): 687-691. JIANG Jianguo, YE Hua, LIU Huimin, et al. Particle swarm optimization method with combination of rapid information communication and local search[J]. Journal of Harbin engineering university, 2015, 36(5): 687-691.

[17]GAO Bingkun, REN Xiuju, XU Mingzi. An improved particle swarm algorithm and its application[J]. Procedia engineering, 2011, 15: 2444-2448.

[18]許少華, 李新幸. 一種自適應改變慣性權重的粒子群算法[J]. 科學技術與工程, 2012, 12(9): 2205-2208. XU Shaohua, LI Xinxing. An adaptive changed inertia weight particle swarm algorithm[J]. Science technology and engineering, 2012, 12(9): 2205-2208.

[19]張建偉, 張立偉, 胡穎, 等. 開源機器人操作系統: ROS[M]. 北京: 科學出版社, 2012.

[20]COUSINS S, GERKEY B, CONLEY K, et al. Sharing Software with ROS[J]. IEEE robotics & automation magazine, 2010, 17(2): 12-14.

[21]ZAMAN S, SLANY W, STEINBAUER G. ROS-based mapping, localization and autonomous navigation using a Pioneer 3-DX robot and their relevant issues[C]//Proceedings of 2011 Saudi International Electronics, Communications and Photonics Conference (SIECPC). Riyadh: IEEE, 2011: 1-5.

Mobile robot multi-goal path planning using improvedparticle swarm optimization

PU Xingcheng1， LI Junjie2， WU Huichao2， ZHANG Yi3

(1.School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065, China; 2.Research Center of Intelligent System and Robot， Chongqing University of Posts and Telecommunications, Chongqing 400065, China; 3.Advanced Manufacturing Engineering School， Chongqing University of Posts and Telecommunications, Chongqing 400065, China)

To solve the problem of multi-goal path planning for mobile robots that pass multiple goals, a new path planning method, based on improved particle swarm optimization (PSO) and ant colony optimization (ACO), is proposed. In this new method, the first step is to use an improved PSO, which has high convergence, to optimize the path between two goals among a sequence of goals. The second step is to use the ACO to obtain the shortest path for all target points. The performance experimental result demonstrates that the improved PSO algorithm can effectively avoid premature convergence and enhances search ability and stability. Simulation results show that the improved PSO algorithm can make a mobile robot realize collision-free multi-goal path planning effectively . Experiments in a real environment demonstrate that this algorithm has practical application for multi-goal path planning.

mobile robot; multi-goal path planning; ACO; improved PSO; opposition-based learning; inertia weight; learning factors

10.11992/tis.201606046

http://kns.cnki.net/kcms/detail/23.1538.TP.20170404.1218.004.html

2016-06-30. 網絡出版日期：2017-04-04.

國家自然科學基金(51604056)，重慶市科學技術委員會項目(cstc2015jcyBx0066)；重慶市教委項目(KJ1400432).

李俊杰. E-mail：lijunjie166@126.com.

TP242.6

A

1673-4785(2017)03-0301-09

蒲興成，男，1973年生，副教授，博士，主要研究方向為非線性系統、隨機系統和現代智能算法。主持重慶郵電大學校級科研項目3項,參與國際合作項目1項,參與省部級項目6項。發表學術論文30余篇,出版著作1部。

李俊杰，男，1990年生，碩士研究生，主要研究方向為移動機器人自主導航。

吳慧超，女，1990年生，碩士研究生，主要研究方向為智能服務機器人。