競爭非局域三次五次非線性介質中孤子的傳輸特性?
黃光僑 林機
(浙江師范大學物理系,金華 321004)
競爭非局域三次五次非線性介質中孤子的傳輸特性?
黃光僑 林機?
(浙江師范大學物理系,金華 321004)
(2016年9月11日收到;2016年12月5日收到修改稿)
研究空間光孤子在一維競爭非局域三次五次非線性介質中的新解和傳輸特性.發現亮孤子在競爭非局域三次自散焦和五次自聚焦非線性介質中存在不穩定區間.在一般非局域程度下,對于不同的三次非線性效應,同相位復合兩孤子間表現為吸引或排斥的相互作用,并討論了折射率的變化.在競爭非局域三次自聚焦和五次自散焦非線性介質中給出了二極、三極和四極孤子能穩定傳播的條件,研究發現更高極孤子的傳播是不穩定的.還研究了孤子功率與傳播常數以及非局域程度的關系.
非局域非線性效應,空間光孤子,穩定性
1 引 言
空間光孤子是線性衍射效應與非線性效應共同作用并精確平衡的結果.材料的非線性空間非局域性是指材料中空間某點的非線性折射率不僅與該點的光場有關,還與該點附近一個區域內的光場有關. 孤子在向列液晶[1?4]、鉛玻璃[5?8]、熱致非線性材料[9]和偶極玻色愛因斯坦凝聚體[10]等材料中表現出非局域非線性物理特性.其中,在向列液晶的非局域介質中亮孤子的吸引和排斥相互作用的臨界值[11],暗孤子長程相互作用產生的穩定束縛態[12],非局域亮孤子在競爭自聚焦和自散焦非線性介質中的相互作用[13],這些特性都表明不同非局域非線性響應對研究空間光孤子的傳輸動力學有重要作用.此外,在非局域非線性克爾介質中,利用李群約化方法給出多種類型光孤子的解析解和Airy數值行波解[14],擴展了Snyder和Mitchell模型的理論分析[15].與Snyder和Mitchell的一維非局域模型相比,Mihalache等[16]在2006年提出的一維競爭非局域三次五次非線性模型,研究了競爭非局域自聚焦三次和自散焦五次非線性介質中亮孤子和偶極孤子的傳輸穩定性,并且證明了基本孤子的穩定性嚴格遵循Vakhitov-Kolokolov定則.Doktorov和Molchan[17]根據Toda鏈模型給出弱非局域三次五次介質中多孤子(鏈孤子)的解析解,并用數值分析孤子與孤子之間的相互補償作用.對于弱非局域三次五次介質,Tosy[18]研究了亮孤子和暗孤子的特點.Zhou等[19]研究了非局域三次五次介質中受到自聚焦和自散焦非線性干擾的暗孤子的特點及其傳輸碰撞的動力學行為.此外,大量研究報道了非局域非線性介質中的多極孤子.在非局域克爾介質中,Xu等[20]發現偶極、三極和四極孤子可以穩定傳輸,但更高階孤子的束縛態則不穩定.Dong等[21]發現在一維熱非線性介質中,三極和四極孤子可在有限非局域范圍內穩定傳輸.
非局域非線性三次自散焦和五次自聚焦介質中的亮孤子和多極孤子以及三次自聚焦和五次自散焦非線性介質中的多極孤子方面的報道較少.本文主要分析非局域非線性三次自散焦和五次自聚焦介質中亮孤子的特點,以及非局域非線性程度對同相位兩孤子之間排斥或吸引等相互作用的影響.研究多極孤子在非局域三次自聚焦和五次自散焦非線性介質中的傳輸穩定性.
2 非局域亮孤子解及其傳輸的穩定性
由Mihalache提出的一維競爭非局域三次五次非線性模型可由非局域非線性薛定諤方程描述為
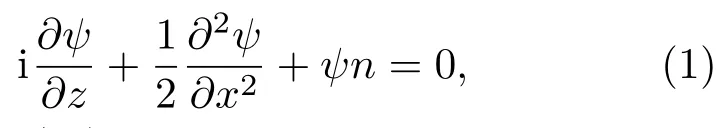
式中ψ為光場振幅,x和z分別為橫坐標上的光束寬度和縱向坐標上的衍射長度,n為誘導折射率.(1)式中非線性項對應光場的誘導折射率為



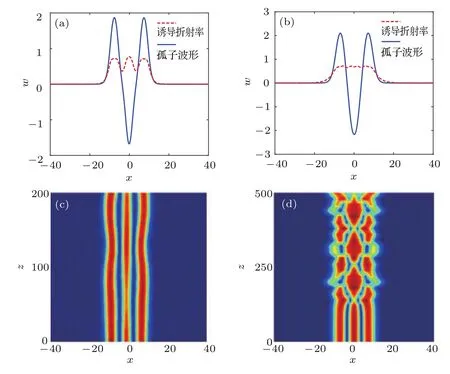
圖1 (網刊彩色)基本孤子的功率和傳播性質 (a)d3=d5=0時功率與傳播常數的關系;(b)d5=10時功率與傳播常數的關系;(c)b=1時孤子的光場波形和誘導折射率;(d)b=0.4時的亮孤子傳輸圖;(e)b=0.6時的亮孤子傳輸圖Fig.1.(color online)Properties of the power and the propagation of the basic solitons:(a)The power versus the propagation constant when d3=d5=0;(b)the power versus the propagation constant when d5=10;(c)the structures of basic optical solitons and the induced refractive index when b=1;(d)propagation of the bright solitons when b=0.4;(e)propagation of the bright solitons when b=0.6.
設(1)式和(2)式中ψ(z,x)=w(x)exp(ibz),其中w為孤子振幅,b為孤子傳播常數.為了研究非局域參數對孤子傳播的影響,預先假定三次自散焦和五次自聚焦的非線性參數分別為a3=?1,a5=2,運用數值計算方法獲得不同非局域參數d3和d5下該模型亮孤子(選取高斯型)的功率和傳輸穩定性,如圖1所示.圖1(a)為局域介質即非局域程度d3=d5=0時的功率曲線,亮孤子功率隨傳播常數b始終是單調遞減的,存在最大功率值Umax=2.6.它與文獻[16]中三次自聚焦和五次自散焦非線性介質中局域亮孤子的功率曲線情況相反,因此,這種局域非線性介質不存在穩定亮孤子.但是研究發現,對于非局域三次自散焦和五次自聚焦非線性介質,亮孤子存在一小段不穩定區間.當非局域程度不同時,孤子功率隨傳播常數先單調遞減后單調遞增,存在一個功率最小值Umin.圖1(b)為d5=10而d3取不同值時亮孤子功率隨傳播常數b的變化曲線.當非局域參數d3=0.3時,傳播常數b=0.259,孤子最小功率Umin=8.755;當d3=3時,傳播常數b=0.463,孤子最小功率Umin=5.972;當d3=10時,傳播常數b=0.117,孤子最小功率Umin=4.393.在dU/db>0區間內存在穩定亮孤子,否則亮孤子不穩定.從圖1(d)可以看出,dU/db<0時,非線性效應較弱,孤子在傳輸過程中發散,而從圖1(e)可以看出,dU/db>0時,衍射效應和非線性效應平衡后亮孤子傳輸穩定性很好.此外,還研究了亮孤子束寬和振幅與非局域程度的關系.從圖1(c)可知,非局域參數d5不變時,隨著非局域參數d3的增加,亮孤子束寬變窄,振幅值變大.在三次自散焦非線性介質中,孤子的誘導折射率波峰向上凸起,這不利于多峰孤子之間的傳輸穩定性.
3 同相位復合兩孤子相互作用的數值分析
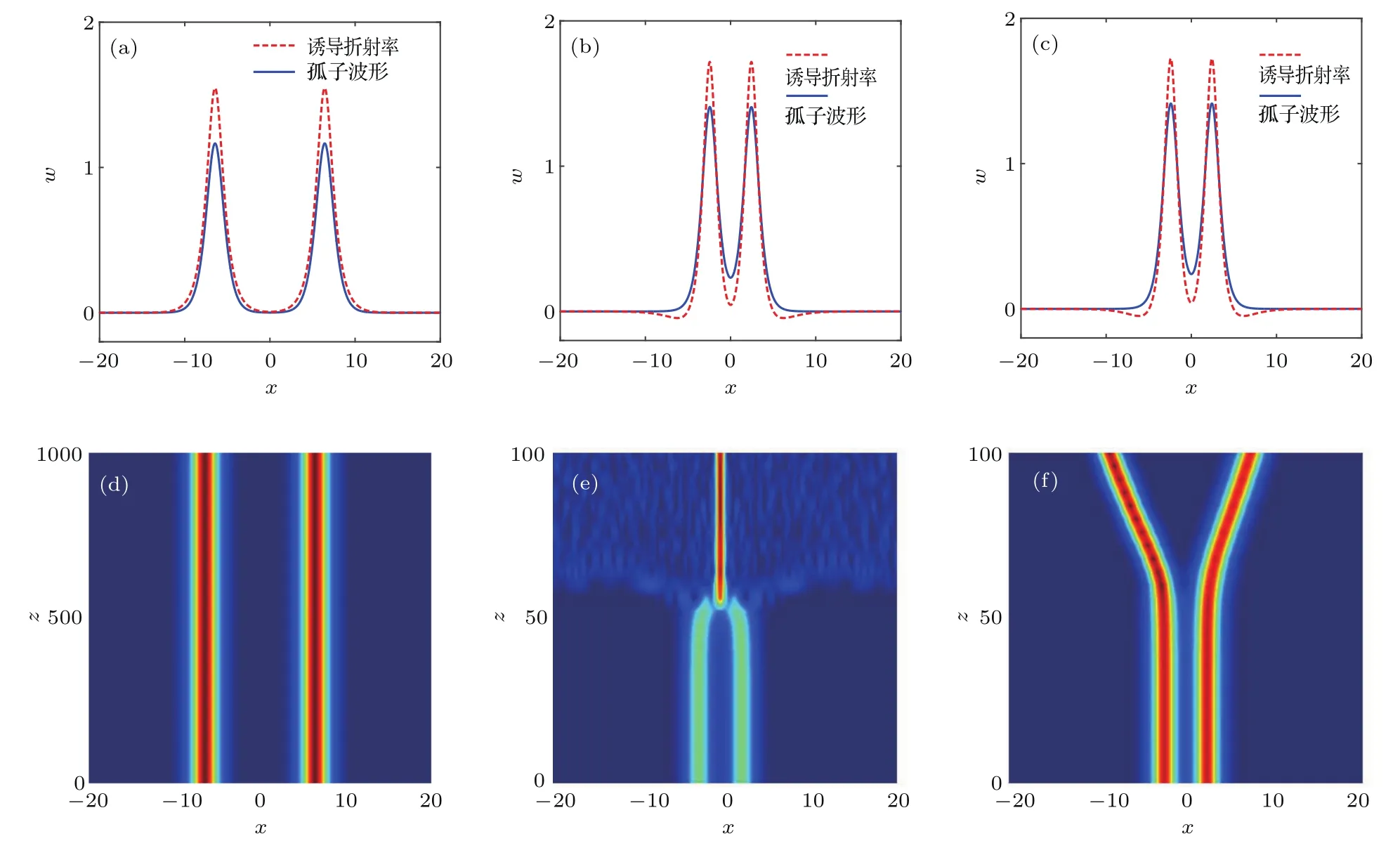
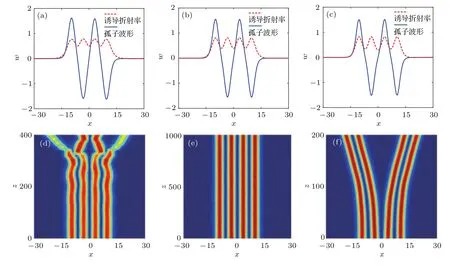
圖2 (網刊彩色)不同非線性參量下同相位兩孤子的相互作用 (a)a3=?0.1,兩孤子間距L=12.876時孤子的光場波形和誘導折射率;(b)a3=?1.69,L=4.878時孤子的光場波形和誘導折射率;(c)a3=?1.73,L=4.822時孤子的光場波形和誘導折射率;(d)a3=?0.1,L=12.876時的孤子傳輸圖;(e)a3=?1.69,L=4.878時的孤子傳輸圖;(f)a3=?1.73,L=4.822時的孤子傳輸圖Fig.2.(color online)The interaction of the two solitons with the same phase for different nonlinear parameters:(a)Soliton structure and induced refractive index when a3=?0.1 and the interval of two solitons L is 12.876;(b)soliton structure and induced refractive index when a3=?1.69 and L=4.878;(c)soliton structure and induced refractive index when a3= ?1.73 and L=4.822;(d)propagation when a3= ?0.1 and L=12.876;(e)propagation when a3=?1.69 and L=4.878;(f)propagation when a3=?1.73 and L=4.822.
本節分別研究非局域參數不變時改變非線性參數和非線性參數不變時改變非局域參數對同相位復合兩孤子的傳播特性的影響.首先,在競爭非局域三次自散焦和五次自聚焦非線性介質中,假定傳播常數b=1,五次非線性參數a5=2,非局域參數d3=2,d5=1,此時復合同相位兩孤子的相互作用特點如圖2所示.當自散焦a3很弱時(圖2(a)),誘導折射率并沒有負的尾部,而且中心位置光場強度為零,引起了排斥作用力,使非線性效應和衍射效應完全平衡,兩個同相位孤子穩定傳輸(圖2(d)).當非局域參數d3>d5時,三次五次非線性響應函數具有負的尾部,相應的誘導折射率兩側分布出現了負區間(圖2).從圖2(b)和圖2(c)可以發現,誘導折射率的中間凹點離x軸的原點都有一定的距離,這將影響兩孤子傳輸的穩定性.當自散焦參數a3達到一個臨界值時,由于自散焦效應,孤子與孤子之間最后會快速分裂排斥傳輸.從圖2(c)可以觀察到當a3達到臨界值時孤子開始分裂,其中的一個孤峰振幅值比另一個孤峰振幅值大.在數值結果中出現兩孤子吸引和分裂的糾纏狀態下其中一個孤峰會因為自散焦作用發散湮沒.當非局域效應較強時,兩孤子會被吸引到一起合并成一個孤子(圖2(e)),與文獻[22]中基本孤子再次出現相互吸引和排斥的交疊狀態傳輸現象不同.當a3減小時兩孤子間距反而增大.對于d5>d3情形,文獻[23]研究表明三次五次非線性響應函數具有負的尾部,而相應的誘導折射率變化也在兩孤子接近x軸尾端為負.
其次,我們研究了非局域程度對兩孤子傳播的影響.假定三次非線性參數a3=?1,其他參數同上,運用數值模擬得到不同非局域參數d3條件下同相位兩孤子相互作用的傳播特點,如圖3所示.當衍射效應和非線性效應達到平衡時,同相位的兩個孤子可以穩定地傳輸(圖3(d)).研究還發現隨著非局域參數d3的增大,兩孤子間距雖然減小,但是兩孤子的相互作用由排斥轉為吸引.這是因為孤子與孤子的中心光場為零,孤子之間總是排斥.當較弱的非局域響應誘導孤子間的吸引作用比排斥作用小時,兩孤子就進行排斥傳輸(圖3(e));反之,兩孤子相互吸引,融合在一起(圖3(f)).
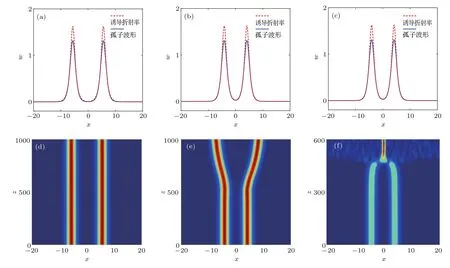
圖3 (網刊彩色)不同非局域程度下同相位兩孤子的相互作用 (a)d3=1.2,L=11.236時孤子的光場波形和誘導折射率;(b)d3=1.38,L=8.308時孤子的光場波形和誘導折射率;(c)d3=1.39,L=8.220時孤子的光場波形和誘導折射率;(d)d3=1.2,L=11.236時的傳輸圖;(e)d3=1.38,L=8.308時的傳輸圖;(f)d3=1.39,L=8.220時的傳輸圖Fig.3.(color online)The interaction of two optical solitons with the same phase for different nonlocal parameters:(a)Soliton structure and induced refractive index when d3=1.2 and L=11.236;(b)soliton structure and induced refractive index when d3=1.38 and L=8.308;(c)soliton structure and induced refractive index when d3=1.39 and L=8.220;(d)propagation when d3=1.2 and L=11.236;(e)propagation when d3=1.38 and L=8.308;(f)propagation when d3=1.39 and L=8.220.
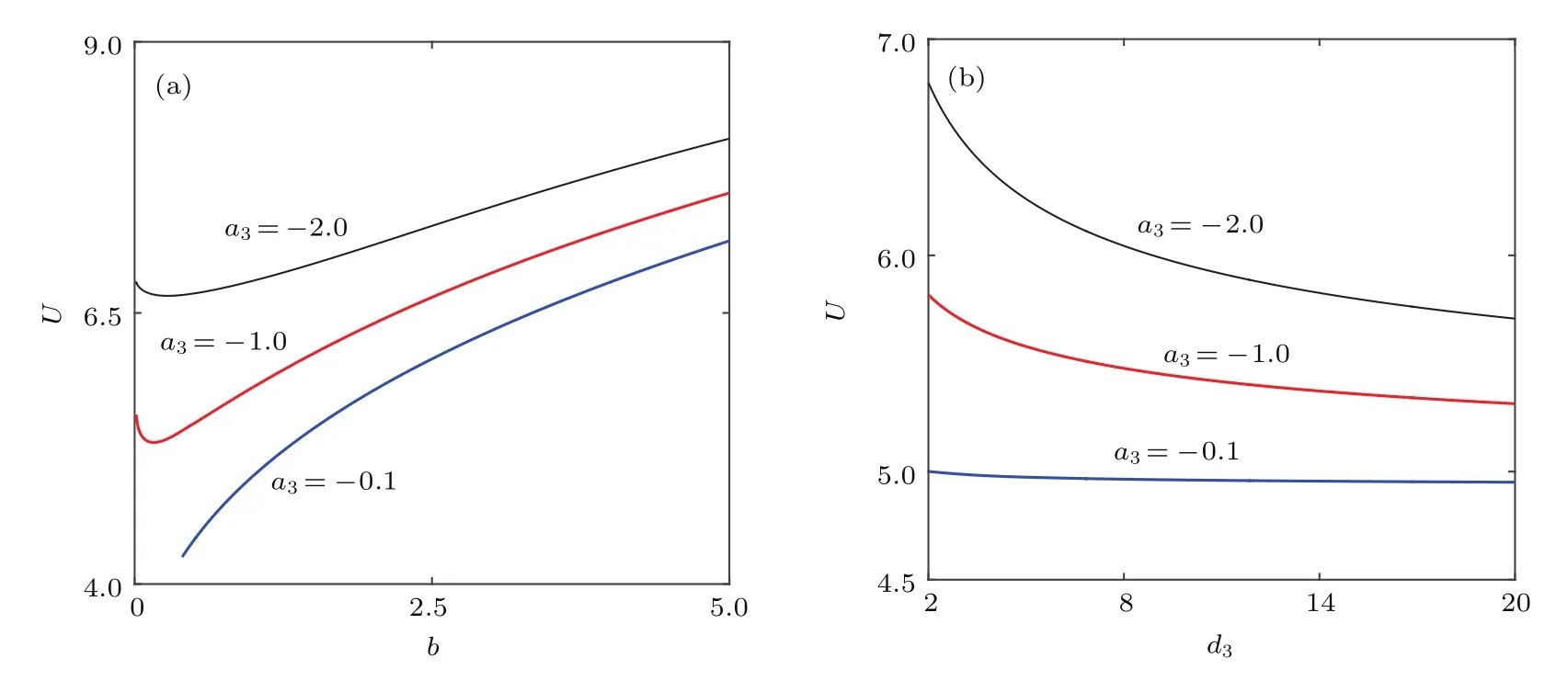
圖4 兩孤子在自散焦介質中的功率曲線 (a)U-b曲線;(b)U-d3曲線Fig.4.The power curves of the two solitons in the self-defocusing medium:(a)U-b curves;(b)U-d3curves.
同時,我們還研究了兩孤子的功率與傳播常數之間的關系.在圖4(a)中,同相位兩孤子的功率隨著傳播常數的變化會因為三次自散焦非線性參數的不同而不同.a3=?0.1時,b<0.39的區間內不存在兩孤子解;當傳播常數b大于該值時,功率值開始單調遞增,這與a3=?1或?2時孤子功率都有先單調遞減再遞增的變化過程不同.a3=?1或?2時,兩孤子都存在最小功率值Umin,分別為5.305和6.658.當功率高于此臨界值時,隨著傳播常數的增加,孤子間距變窄而振幅值變大.從圖4(b)可發現,在相對弱非線性a3=?0.1條件下,U?d3曲線基本上與x軸平行,這時自散焦作用影響很弱,容易出現穩定傳輸的同相位兩孤子.而在其他非線性a3參數下,功率U都是隨著d3單調遞減.
我們還對三極孤子、四極孤子和五極孤子的傳播穩定性進行了數值計算,發現在一定的參數條件下孤子能穩定傳輸,但是對六極孤子及以上的孤子沒有找到合適的參數使其穩定傳播.
4 競爭非局域多極孤子的傳輸特性
為了研究競爭非局域三次五次非線性介質中多極孤子的傳輸穩定性,將(1)式和(2)式的初始輸入加白噪聲ψ(x,z=0)=w(x)[1+ρ(x)],其中ρ(x)為高斯分布的隨機噪聲且方差δ2=0.01.將以上初始條件代入(1)式和(2)式,并利用分步傅里葉方法進行數值模擬得到白噪聲擾動下的多極孤子傳輸圖像.以下主要討論在競爭非局域三次自聚焦和五次自散焦非線性介質中的多極孤子的特點及其傳輸特性.
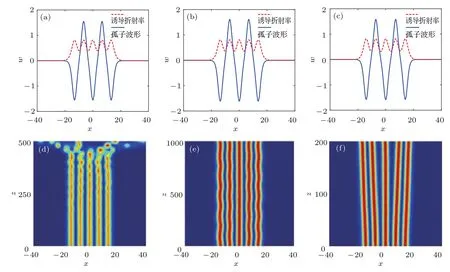
由三個不同相位的孤子組成的三極孤子(也稱為束縛態)在競爭非局域三次五次非線性介質中可以穩定傳輸.不同非局域程度下三極孤子的特點和傳輸特性如圖5所示.給定傳播常數b=0.6、非線性參量a3=1,a5=?0.23和非局域參數d3=3,從圖5(a)—(c)可以看出,隨著非局域參數d5的增大,三極孤子光束束寬變窄,振幅值變小,功率也減小.相位相反的孤子之間存在排斥作用,所以當非局域參數d5小于某一個閾值時,三極孤子的兩側孤子無法被排斥傳輸,而是出現振蕩傳輸,并且融合后能分裂出兩個孤峰(圖5(d)).當非局域參數4 四極孤子由兩兩反相孤子所構成,所以它們之間既有排斥作用,又有相互吸引作用.圖7為不同非局域程度下四極孤子的特點和傳輸特性.給定b=0.6,a3=1,d3=3,d5=5,減小五次非線性參量a5值時,孤子之間的吸引作用增強,同時孤子的振幅值也相應增大;反之,孤子排斥作用增大,幅值減小.僅在a5=?0.23處吸引作用和排斥作用相互平衡,出現穩定傳輸的四極孤子(圖7(e)),在自散焦非線性a5 圖5 (網刊彩色)不同非局域程度下三極孤子的特點和傳輸特性 (a)d5=1時孤子的光場波形和誘導折射率;(b)d5=5時孤子的光場波形和誘導折射率;(c)d5=8時孤子的光場波形和誘導折射率;(d)d5=1時加δ2=0.01白噪聲的傳輸圖;(e)d5=5時加δ2=0.01白噪聲的傳輸圖;(f)d5=8時加δ2=0.01白噪聲的傳輸圖Fig.5.(color online)The characteristics and the propagation properties of the triple-pole solitons for different nonlocal parameters:(a)Soliton structure and induced refractive index when d5=1;(b)soliton structure and induced refractive index when d5=5;(c)soliton structure and induced refractive index when d5=8;(d)propagation with the white noise of δ2=0.01 when d5=1;(e)propagation with the white noise of δ2=0.01 when d5=5;(f)propagation with the white noise of δ2=0.01 when d5=8. 由以上的數值結果分析可得,參數b=0.6,a3=1,a5=?0.23,d3=3,d5=5時也可能會出現穩定的五極孤子.然而,圖8(d)中的數值模擬結果表明在該參數條件下不存在穩定傳輸的五極孤子.為了找出傳輸更加穩定的五極孤子,嘗試增加五次非線性參量a5=?0.24.由圖8(e)發現五極孤子加白噪聲情況下,除中間孤子外其他孤子都呈波浪式不穩定傳輸.與a5=?0.23時的傳輸相比,該非局域程度的五極孤子傳輸更加穩定,也說明前者五個孤子之間的排斥作用較弱,不足以使五極孤子穩定傳輸.隨著非局域參數d5的減小,五極孤子傳輸已經變得沒有規則,隨時有坍塌現象發生.而在d5>6的情況下,孤子與孤子的排斥作用增強,五極孤子除中間的孤子外,其他四個孤子以最快的速度排斥傳輸.通過大量的數值計算發現,在其他參數不變情況下,只在d3 圖6 (網刊彩色)不同非局域非線性下三極孤子的特點和傳輸特性 (a)a3=0.95,a5=?0.22,d3=d5=2時孤子的光場波形和誘導折射率結構圖;(b)a3=1,a5=?0.2,d3=d5=8時孤子的光場波形和誘導折射率結構圖;(c)a3=0.95,a5=?0.22,d3=d5=2時三極孤子加δ2=0.01白噪聲的傳輸圖;(d)a3=1,a5=?0.2,d3=d5=8時不加微擾的不穩定傳輸圖Fig.6.(color online)The characteristics and the propagation properties of the triple-pole solitons for the different nonlocal nonlinear parameters:(a)Soliton structure and induced refractive index when a3=0.95,a5=?0.22,and d3=d5=2;(b)soliton structure and induced refractive index when a3=1,a5=?0.2,and d3=d5=8;(c)propagation of the triple-pole solitons with the white noise of δ2=0.01 when a3=0.95,a5= ?0.22,and d3=d5=2;(e)propagation without white noise when a3=1,a5=?0.2,and d3=d5=8. 圖7 (網刊彩色)不同非局域程度下四極孤子的特點和傳輸特性 (a)d5=3時孤子的光場波形和誘導折射率;(b)d5=5時孤子的光場波形和誘導折射率;(c)d5=8時孤子的光場波形和誘導折射率;(d)d5=3時加δ2=0.01白噪聲的傳輸圖;(e)d5=5時加δ2=0.01白噪聲的傳輸圖;(f)d5=8時加白噪聲δ2=0.01的傳輸圖Fig.7.(color online)The characteristics and the propagation properties of the quadrupole solitons for the different nonlocal parameters:(a)Soliton structure and induced refractive index when d5=3;(b)soliton structure and induced refractive index when d5=5;(c)soliton structure and induced refractive index when d5=8;(d)propagation with the white noise of δ2=0.01 when d5=3;(e)propagation with the white noise of δ2=0.01 when d5=5;(f)propagation with the white noise of δ2=0.01 when d5=8. 圖8 (網刊彩色)不同非局域程度下五極孤子的特點和傳輸特性(a)a5=?0.23,d3=3,d5=5時孤子的光場波形和誘導折射率結構圖;(b)a5=?0.24,d3=3,d5=5時孤子的光場波形和誘導折射率結構圖;(c)a5=?0.24,d3=3,d5=6時孤子的光場波形和誘導折射率結構圖;(d)a5=?0.23,d3=3,d5=5時加δ2=0.01白噪聲的傳輸圖;(e)a5=?0.24,d3=3,d5=5時加δ2=0.01白噪聲的傳輸圖;(f)a5=?0.24,d3=3,d5=6時加δ2=0.01白噪聲的傳輸圖Fig.8.(color online)The characteristics and the propagation properties of the penta-pole solitons for different nonlocalities:(a)Soliton structure and induced refractive index when a5=?0.23,d3=3,and d5=5;(b)soliton structure and induced refractive index when a5=?0.24,d3=3,and d5=5;(c)soliton structure and induced refractive index when a5=?0.24,d3=3,and d5=6;(d)propagation with the white noise of δ2=0.01 when a5= ?0.23,d3=3,and d5=5;(e)propagation with the white noise of δ2=0.01 when a5= ?0.24,d3=3,and d5=5;(f)propagation with the white noise of δ2=0.01 when a5=?0.24,d3=3,and d5=6. 運用數值計算方法研究了競爭非局域三次五次非線性介質中不同類型空間光孤子的存在和傳播穩定性.在非局域三次自散焦和五次自聚焦的非線性介質中亮孤子的功率隨傳播常數的變化曲線并不是單調遞增的,孤子存在不穩定區間.一般非局域程度下同相位復合的兩孤子考慮不同的非線性效應時,其相互作用具有不同性質.此外,還給出了非局域非線性三次自聚焦和五次自散焦介質中的多極孤子穩定性條件,在滿足一定的參數關系時,二極、三極和四極孤子能穩定傳播,但不存在五極以上(包括五極)的穩定傳播的孤子.對以上所有情形,都給出了折射率的數值計算結果. [1]Conti C,Peccianti M,Assanto G 2003Phys.Rev.Lett.91 073901 [2]Conti C,Peccianti M,Assanto G 2004Phys.Rev.Lett.92 113902 [3]Fratalocchi A,Assanto G,Brzdakiewicz K A,Karpierz M A 2004Opt.Lett.29 1530 [4]Conti C,Peccianti M,Assanto G 2006Opt.Lett.31 2030 [5]Dabby F W,Whinnery J R 1968Appl.Phys.Lett.13 284 [6]Rotschild C,Cohen O,Manela O,Segev M,Carmon T 2005Phys.Rev.Lett.95 213904 [7]Xie Y Q,Guo Q 2004Acta Phys.Sin.53 3020(in Chinese)[謝逸群,郭旗 2004物理學報 53 3020] [8]Cao J N,Guo Q 2005Acta Phys.Sin.54 3688(in Chinese)[曹覺能,郭旗 2005物理學報 54 3688] [9]Ghofraniha N,Conti C,Ruocco G,Trillo S 2007Phys.Rev.Lett.99 043903 [10]Burger S,Bongs K,Dettmer S,Ertmer W,Sengstock K,Sanpera A,Shlyapnikov G V,Lewenstein M 1999Phys.Rev.Lett.83 5198 [11]Rasmussen P D,Bang O,Krolikowski W 2005Phys.Rev.E72 066611 [12]Nikolov N I,Neshev D,Krolikowski W,Bang O,Rasmussen J J,Christiansen P L 2004Opt.Lett.29 286 [13]Esbensen B K,Bache M,Bang O,Krolikowski W 2012Phys.Rev.A86 033838 [14]Jia J,Lin J 2012Opt.Express20 7469 [15]Snyder A W,Mitchell D J 1997Science276 1538 [16]Mihalache D,Mazilu D,Lederer F,Crasovan L C,Kartashov Y V,Torner L,Malomed B A 2006Phys.Rev.E74 066614 [17]Doktorov E V,Molchan M A 2008J.Phys.A:Math.Theor.41 315101 [18]Tsoy E N 2010Phys.Rev.A82 063829 [19]Zhou Z X,Du Y W,Hou C F,Tian H,Wang Y 2011J.Opt.Soc.Am.B28 1583 [20]Xu Z Y,Kartashov Y V,Torner L 2005Opt.Lett.30 3171 [21]Dong L W,Ye F W 2010Phys.Rev.A81 013815 [22]Kartashov Y V,Vysloukh V A,Torner L 2008Opt.Lett.33 1747 [23]Du Y W,Zhou Z X,Tian H,Liu D J 2011J.Opt.13 015201 PACS:42.70.Nq,42.65.Sf DOI:10.7498/aps.66.054208 Propagating properties of spatial solitons in the competing nonlocal cubic-quintic nonlinear media? Huang Guang-Qiao Lin Ji? (Department of Physics,Zhejiang Normal University,Jinhua 321004,China) 11 September 2016;revised manuscript 5 December 2016) We study the new spatial optical solitons and their propagating properties in the one-dimensional nonlocal cubicquintic(C-Q)nonlinear model by the numerical method.We obtain multi-bright solitons and multipole soliton solutions in the one-dimensional nonlocal C-Q nonlinear model.The propagation of bright solitons is stable in the competing nonlocal cubic self-defocusing and quintic self-focusing nonlinear media when these nonlocal and nonlinear parameters are in the appropriate value domain.Considering the different nonlinear cubic effects,the interaction between two optical solitons with the same phase in the general nonlocal media displays the attraction or the repulsion for different nonlocal and nonlinear parameters.We find that the interval of two solitons affects the interaction between them.The refractive index is changed with the propagating constant when the nonlocal constantd3is 10.Moreover,the triplepole,quadrupole and pentapole solitons can propagate steadily when the nonlocal parameters are appropriate,but hexa-pole(or above)solitons propagate unsteadily for any nonlocal parameter.Furthermore,we investigate the multi-pole solitons and their propagation stabilities by the Newton difference method and the Fourier split step method,obtain the stable propagation conditions for dipole,triplepole and quadrupole solitons,and find that the propagation of the pentapole and higher-order pole solitons is unstable.We also discuss the interactions of multi-pole solitons when they propagate along the axisz.The interactions are attraction or repulsion when the nonlocal and the nonlinear parameters are different.Meanwhile,we simulate the evolution of the refractive index along the axiszwhen the spatial optical solitons are multi-pole solitons.Finally,we study the relation between the power of soliton and the propagation constant under different degree of nonlocality.The power of the single bright soliton does not monotonically increase with the increasing propagation constant when the degree of nonlocalityd3is 10.We also derive the relation between the power of dipole bright solitons with the cubic nonlinearity parameter and the propagation constant under different degree of nonlocality.The power decreases monotonically with the increasing propagation constant when the cubic nonlinearity is a certain value or with the increasing cubic nonlinearity when the propagation constant is a certain value. nonlocal nonlinear effect,spatial optical solitons,stability PACS:42.70.Nq,42.65.Sf 10.7498/aps.66.054208 ?浙江省自然科學基金重點項目(批準號:LZ15A050001)和國家自然科學基金(批準號:11675146)資助的課題. ?通信作者.E-mail:linji@zjnu.edu.cn *Project supported by the National Natural Science Foundation of Zhejiang Province,China(Grant No.LZ15A050001)and the National Natural Science Foundation of China(Grant No.11675146). ?Corresponding author.E-mail:linji@zjnu.edu.cn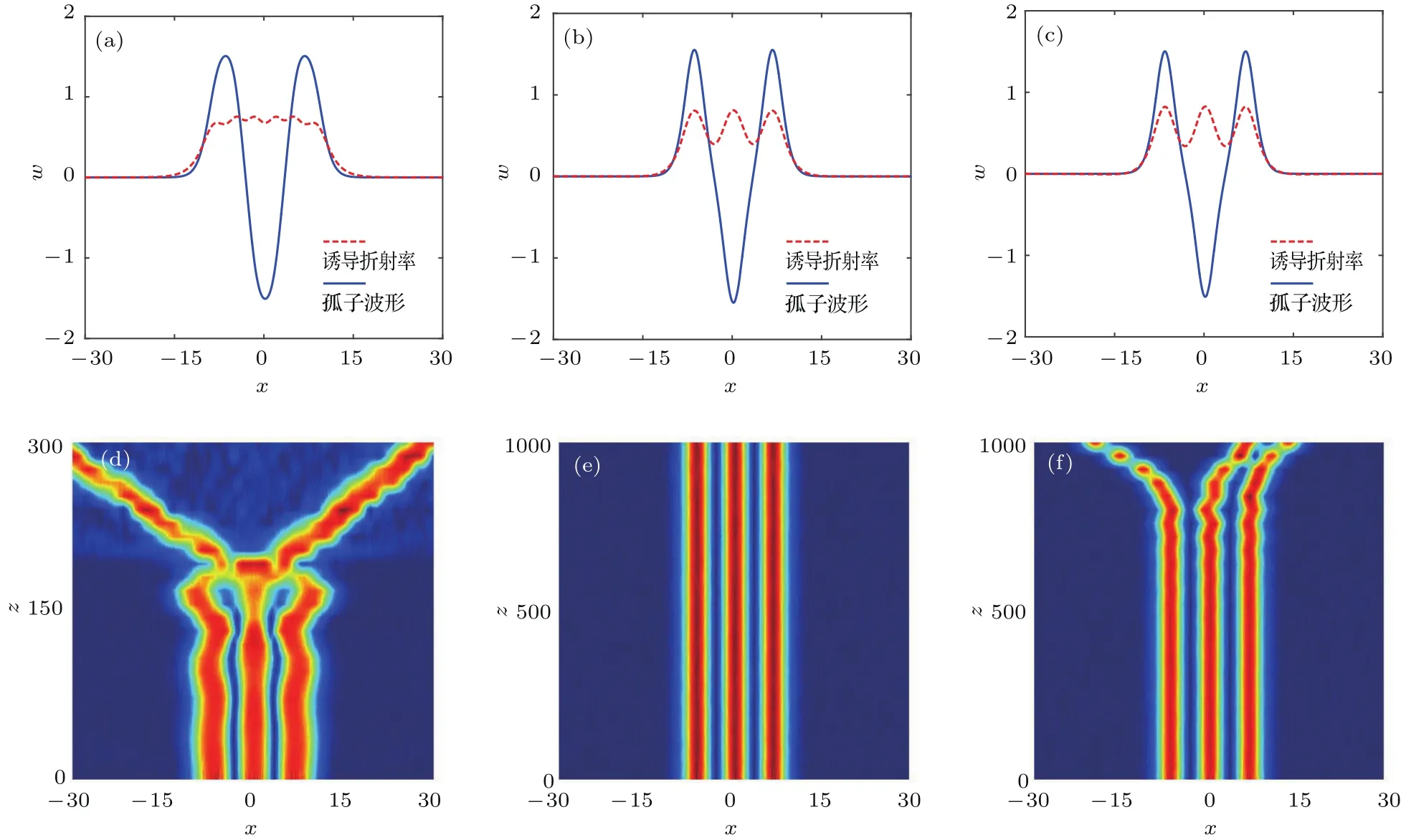
5 結 論

