微滴撞擊織物表面沉積過程建模研究

肖 淵， 申 松， 張津瑞， 劉金玲， 吳 姍， 楊鵬程

(西安工程大學 機電工程學院 陜西 西安 710048)

微滴撞擊織物表面沉積過程建模研究

肖 淵， 申 松， 張津瑞， 劉金玲， 吳 姍， 楊鵬程

(西安工程大學 機電工程學院 陜西 西安 710048)

為明確微滴與織物表面的碰觸、鋪展及滲透機理，基于最小勢能原理，得到了紗線的中心線模型，通過研究纖維在紗線截面內的分布規律以及纖維體積分數的計算方法，建立了織物單胞的二維幾何模型.在上述建立的織物模型基礎上，依據流體體積(volume of fluid， VOF)兩相流模型，建立了單顆微滴撞擊織物表面后沉積變形的模型.利用所建立的模型，進行微滴與織物基底的碰撞及滲透過程仿真研究，并將模擬過程與試驗進行對比. 結果表明，所建模型可實現對微滴在織物基底的碰撞及滲透過程的模擬，整個過程與試驗結果吻合較好.該研究方法與結果為后續不同工藝參數下微滴在織物表面沉積過程的研究奠定了基礎.

織物； 建模； 纖維分布； 微滴； 沉積； 碰撞； 滲透

智能紡織品是一種將紡織品與電子信息技術高度融合的新型紡織品.它是將傳感器、執行器、數據處理、通信、電源等單元集成到紡織品中，使之具備信息采集、信息識別、檢測反饋、積累與響應等功能，可以實現自診斷、自修復和自適應等能力，在軍事、航空、航天、生物醫學、體育休閑、娛樂、醫療保健等領域有著重要的應用前景[1].如何將電子元件與紡織品有效集成，使其不僅滿足織物功能需求，還能保證紡織品的耐水洗、耐磨損及穿著舒適是智能紡織品研究的焦點.將微滴按需噴射3D打印技術與化學沉積相結合，再將金屬鹽和還原劑溶液精確打印在織物表面的指定位置，從而在室溫下還原出金屬微粒，可以實現微細導電線路的直接打印成形[2].但在織物表面微滴噴射打印沉積過程中，因織物表面與一般固體基板不同，具有高粗糙度和多孔等復雜特征.試驗手段只能觀測微滴在織物表面的形態變化，無法掌握內部壓力場變化及微滴在織物截面內的滲透過程.基于此，本文通過建立微滴與織物基板碰撞及滲透過程的理論模型，對微滴與織物基板碰撞、滲透過程進行研究，為后續打印高質量微細導電線路奠定理論基礎.

國內外學者對微滴在不同基板的沉積過程進行了較為深入的研究.文獻[3-5]采用VOF(volume of fluid)法實現了金屬熔滴在固體基板沉積和凝固過程的模擬. Bussmann等[6]建立了液滴與固壁碰撞的三維模型，采用有限差分法在固定網格上求解動量和能量守恒方程，以VOF方法跟蹤液滴在自由表面的流動.李素麗等[7]利用建立的VOF模型對整個熔滴沉積流固耦合過程進行數值模擬，分析了熔滴滴落及在基板壁面上的鋪展狀態.Verleye等[8]針對無皺褶織物和平紋織物建立了細觀幾何模型，模擬了樹脂在織物單胞內的流動.Chen等[9]采用FLOTRAN CFD軟件對織物模型進行了簡化，模擬了樹脂在平紋織物紗線區域內的流動.戴福洪等[10]建立了平紋織物的幾何結構模型，采用均勻化方法預測了樹脂在該模型中的滲透率.上述研究主要集中在微滴與固體基板碰撞以及微滴在織物內紗線間滲透兩方面.但是針對微滴在紗線內部纖維間滲透過程的動態仿真及其試驗驗證的研究較少.本文以平紋織物為研究對象，在充分考慮紗線內部可滲透性基礎上，建立織物的二維幾何模型；采用VOF法建立單顆液滴在織物表面的沉積碰撞、滲透模型，利用所建立的模型對液滴在織物基板的沉積變形過程進行研究，明確微滴在織物表面的沉積過程，為后續織物表面導電線路的精確沉積奠定基礎.

1 紗線模型的建立

確定紗線模型是織物建模的基礎，在其建模過程中，通常依據紗線截面形態和中心線的屈曲形態構成紗線的包絡曲面，來表示紗線的整體形狀. 紗線模型的建立包括紗線中心線模型、紗線截面模型、纖維分布模型以及纖維體積分數的計算方法.

1.1 紗線中心線模型

常見的紗線中心線模型有正弦曲線、貝塞爾曲線、B樣條曲線、自然三次樣條曲線等.本文基于最小勢能原理求解得到紗線中心線的幾何表達式，從而得到更接近實際的紗線中心線模型.平紋織物紗線編織結構如圖1所示，其中曲線z(x)表示紗線的中心線路徑，T表示織物厚度，S表示相鄰紗線中心線的間隔，h表示紗線厚度，w表示紗線寬度，h0表示紗線卷曲高度.

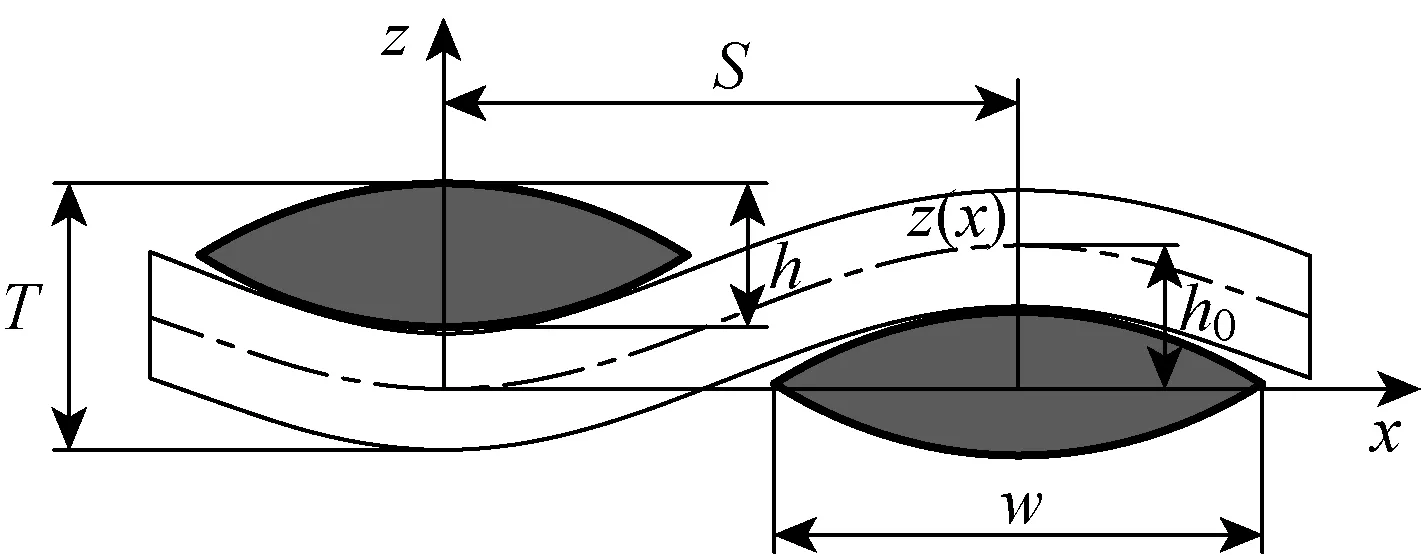
圖1 平紋織物編織結構圖Fig.1 Plain fabric weave structure

在彎曲間隔S內單根紗線彎曲勢能為

(1)

式中：W為彎曲勢能；B為紗線彎曲剛度；括號內式子表示紗線中心線曲率.對單根卷曲紗線利用最小勢能原理，可得紗線中心線路徑的表達式z(x)的近似結果為

(2)

1.2 紗線截面模型

紗線的橫截面有圓形、橢圓形、跑道形、透鏡形等.由于經緯紗在交叉處相互受力而形成類似于透鏡形截面.該截面是由兩個半徑分別為r1和r2的圓交叉而成.由于經緯紗在交叉時有力的作用產生，紗線截面的上部分會在力的作用下向下壓而發生變形，使其產生變形距離d，截面其他部分的參數如半徑r1、r1以及圓心O1、O2縱坐標y1、y2可由紗線寬度w、高度h以及變形距離d根據式(3)～(6)計算而來.

(3)

(4)

(5)

(6)

透鏡形紗線截面的參數方程如下：

(7)

(8)

(9)

兩種典型的透鏡形紗線截面如圖2所示，如果紗線變形距離d=0，則兩個圓的半徑和偏移量相等，這是理想的狀態下，兩段圓弧成對稱形分布(圖2(a)).實際上，紗線在編織過程中不可避免地會產生扭曲變形，圖2(b)更接近真實的織物紗線截面形狀.

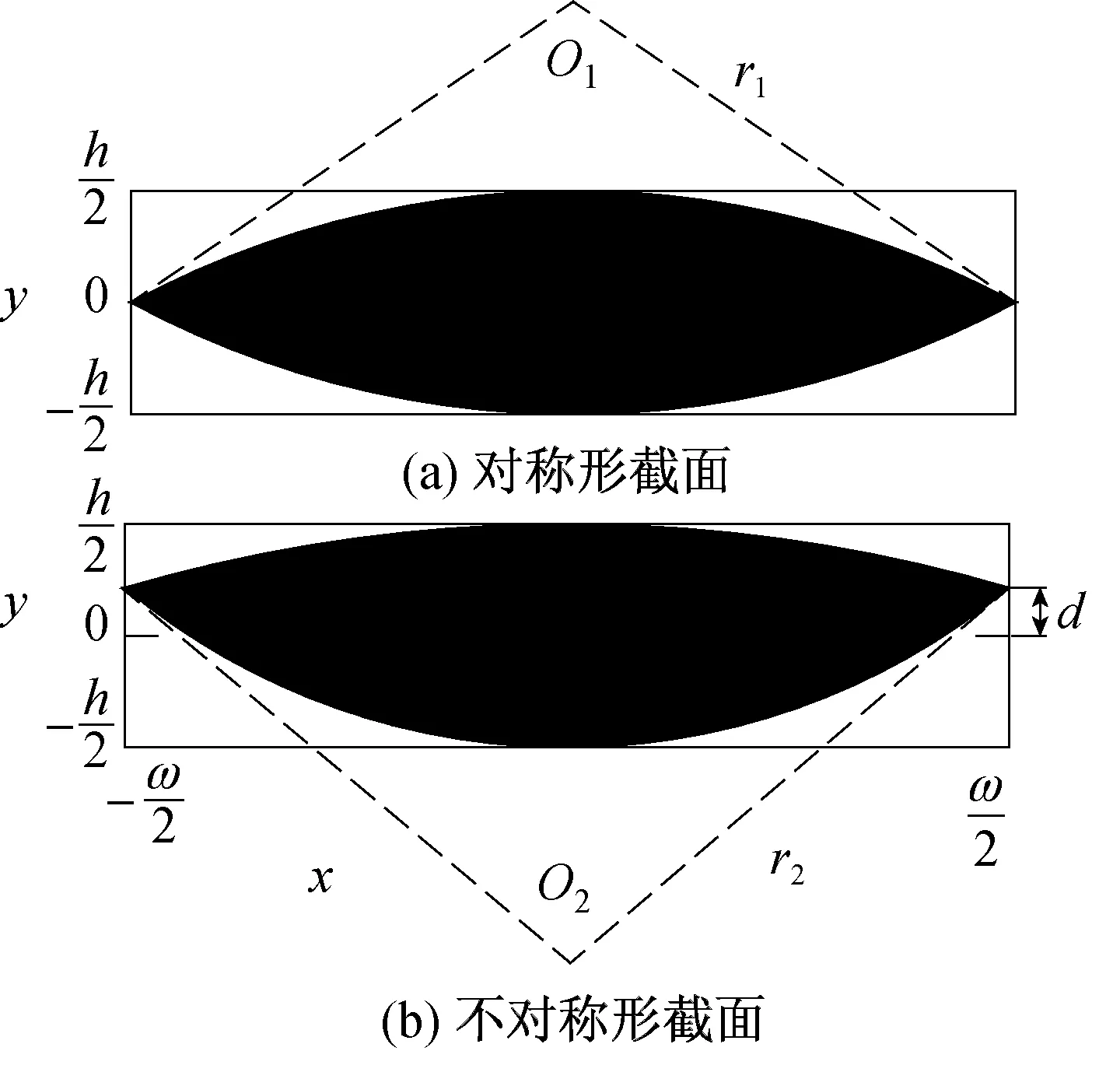
圖2 透鏡形紗線截面Fig.2 Lenticular cross-section of the yarn

1.3 纖維分布模型

單根紗線是由多根纖維以一定的捻度扭曲而成，因纖維在紗線內的分布受多種因素影響，為簡化計算做如下假設[11-12]：

(1) 纖維以半徑相等的圓分布于紗線截面內；

(2) 纖維在紗線截面內按層分布；

(3) 同一層纖維的圓心分布于一條曲線上.

因此，確定纖維圓心的分布曲線，使纖維以一定的間隙分布于紗線截面上是纖維建模的關鍵. 為獲得纖維圓心的分布曲線，需先確定曲線所在的截面C(t，μ).引入兩個橫截面A(t)和B(t)(整個紗線截面)，其關系如下所示：

C(t，μ)=A(t)+(B(t)-A(t))μ

0≤t≤1 0≤μ≤1

(10)

式中：μ在截面A(t)和B(t)從0到1成線性變化，從而使纖維在層與層之間平穩過渡.圖3為透鏡形紗線截面內纖維圓心分布的曲線圖.

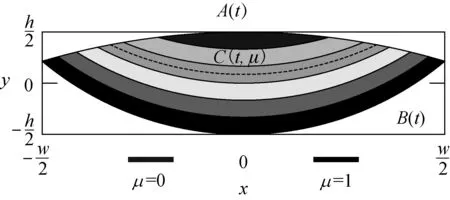
圖3 透鏡形截面內纖維圓心分布曲線圖Fig.3 Distribution of circle of fiber center in the lenticular cross-section

為了使纖維層與層之間具有更好的連續性，采用一個三次方程式來表示μ與x之間的關系.

當x=0時

μ=0

(11)

當x=L時，L為纖維層與層之間的距離，則

μ=1

(12)

因此，可得如下方程：

(13)

1.4 纖維體積分數

確定纖維的多少及纖維的間距，對后續研究微滴在織物內滲透性至關重要.圖4為紗線截面內纖維體積分數示意圖，其中，AF為紗線截面內纖維的面積，AY為紗線截面面積.

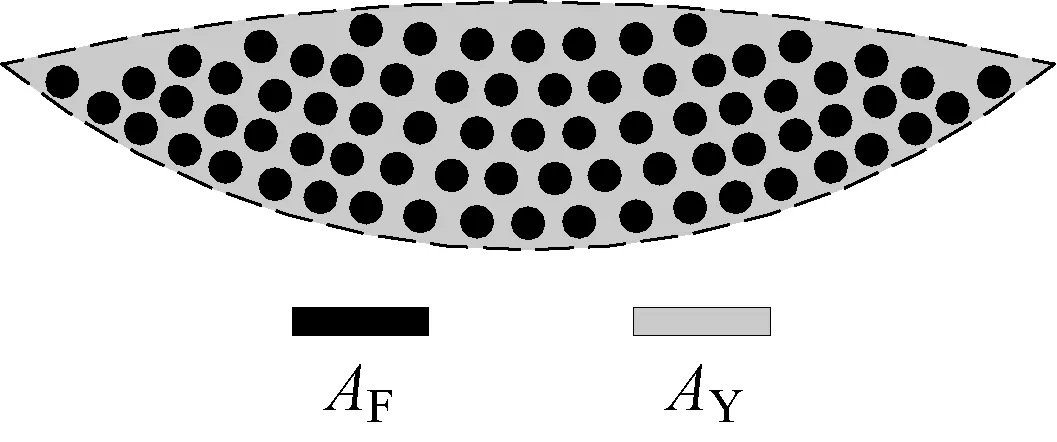
圖4 紗線截面內纖維體積分數示意圖Fig.4 Fiber volume fraction in the yarn cross-section

建模時，通過試驗測量紗線或織物的質量m，計算出紗線或織物總的纖維體積VF，假設所有纖維的密度ρ相等，則：

(14)

利用式(15)可計算出紗線中纖維的體積分數φF

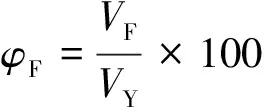
(15)

式中：VY為紗線體積.

此種方法得到的是整個紗線或織物的纖維體積分數，適于紗線橫截面沿著紗線方向不發生顯著變化的情況. 但是對于大多數紗線截面發生變化的情況，一個截面內纖維的面積AF與紗線截面面積AY的比例更能反映纖維體積分數. 假設纖維是不可壓縮的且纖維面積在紗線截面內沿著紗線長度方向不發生變化. 因此纖維面積分數ωF為：

(16)

給定紗線的線密度ζ和組成纖維的密度ρ,則：

(17)

2 平紋織物模型的建立

由于織物結構的復雜性，處于不同編織結構和受力狀態下的織物幾何結構差距較大，本節利用文獻[13]給出的滌綸平紋織物建立幾何模型，其實物照片和詳細參數設置如圖5和表1所示.

圖5 平紋織物實物圖[13]Fig.5 Plain fabric

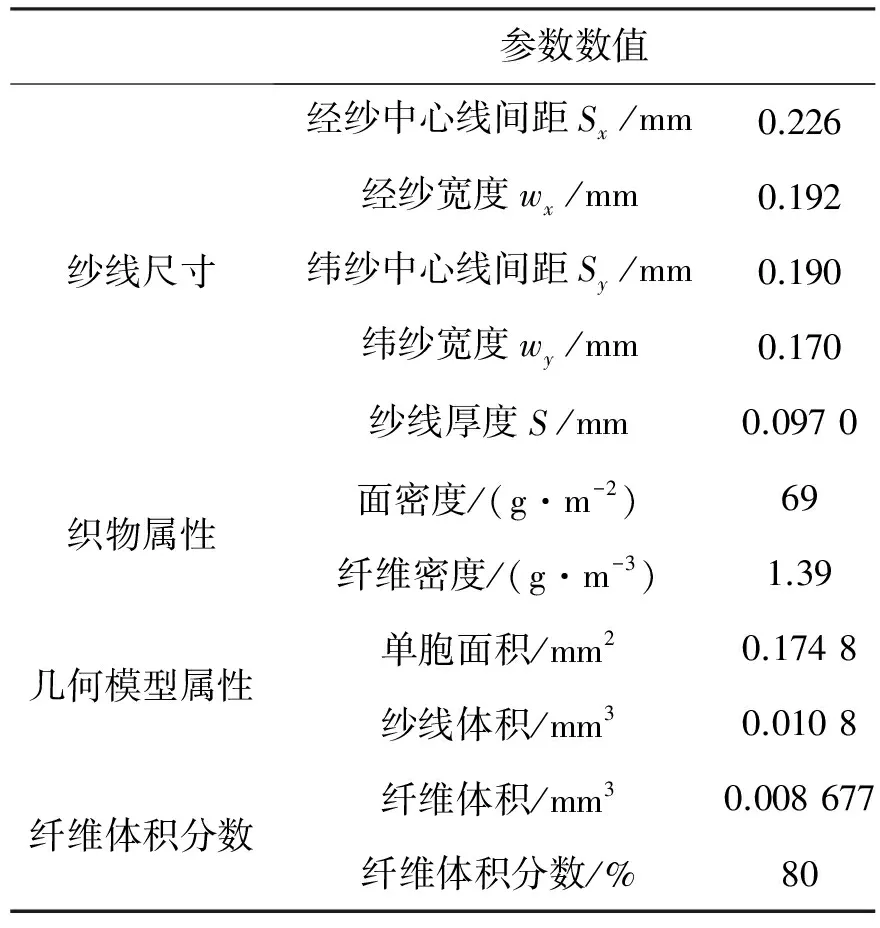
表1 Chomarat 150 TB織物參數[13]

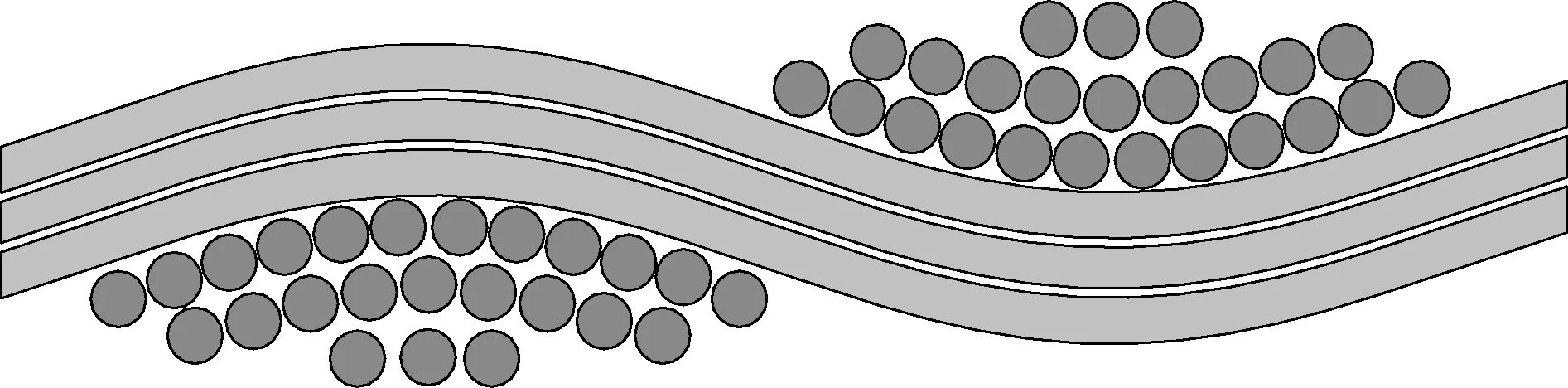
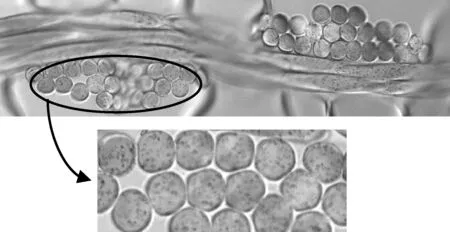
利用表1中參數，建立織物的二維幾何模型如圖6(a)所示，圖6(b)為實際織物紗線截面SEM圖[13].

(a) 所建立的織物幾何模型

(b) 紗線截面SEM圖

圖6 織物幾何模型

Fig.6 Fabric geometry model

由圖6可看出一個單胞由兩根經紗和兩根緯紗組成.經紗內纖維分三層分布，依次有12根、9根、3根共24根纖維組成.而垂直于經紗方向的緯紗由三層纖維組成.由紗線截面內纖維分布放大圖可以明顯地看出，纖維之間以及纖維層與層之間都有一定的間隙.通過對比實際織物的SEM圖，可以看出建立的幾何模型與真實織物較一致.

3 織物表面微滴沉積過程建模

為了研究微滴在織物表面的沉積過程，本節采用Fluent 軟件中的VOF兩相流模型建立控制方程，通過求解單獨動量方程和處理穿過區域的每一流體的體積比來模擬兩種以上不相容流體.該過程涉及液滴和空氣兩種流體，假設二者間無熱傳質、非壓縮流體，且黏性系數、表面張力系數等都是常數.

3.1 流動控制方程組

根據VOF方法，通過求解連續性方程

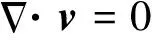
(18)

式中：v為速度矢量.

用體積分數γ來追蹤氣液交界面.對液相流體，γ=0表示單元是空的，γ=1表示單元充滿，0<γ<1表示單元為氣液兩相界面.VOF模型中，動量方程為

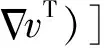
(19)

ρ=γ1ρ1+(1-γ1)ρ0

(20)

μ=γ1μ1+(1-γ1)μ0

(21)

式中:F為表面張力源項；p為壓力；g為重力矢量；ρ為計算單元內密度；μ為計算單元內動力黏度；下標0表示氣相，1表示液相.

表面張力源項采用Brackbill提出的連續表面力(CSF)模型來求解. 能量方程為

(22)

式中：cp為計算單元內比熱容；T為計算單元內溫度；λ為計算單元內導熱系數.

對于流體在紗線內部的流動，將紗線看作多孔介質，采用Brinkman方程描述流體流動，如式(23)所示.

(23)

式中：Kyarn為紗線的滲透率張量.

3.2 計算區域的確定

由于各部分流體在沉積過程中始終沿軸向對稱分布，為減少計算時間，只對區域的1/2進行求解并擴展至整個區域. 本文采用二維模擬，計算區域為738 μm×600 μm，包括流體區域(A區液滴和B區空氣)和多孔區域(C區織物)，A和B區采用四邊形均勻網格劃分，C區采用非結構化網格劃分，計算區域網格總數為17 146.計算區域和邊界條件如圖7所示，設邊界處的壓強為1.01×105Pa，液滴與壁面間采用無滑移邊界條件.液滴表面為研究的自由表面，液滴周圍為大氣環境，求解時需考慮重力的影響，且重力加速度方向與液滴下落方向一致.

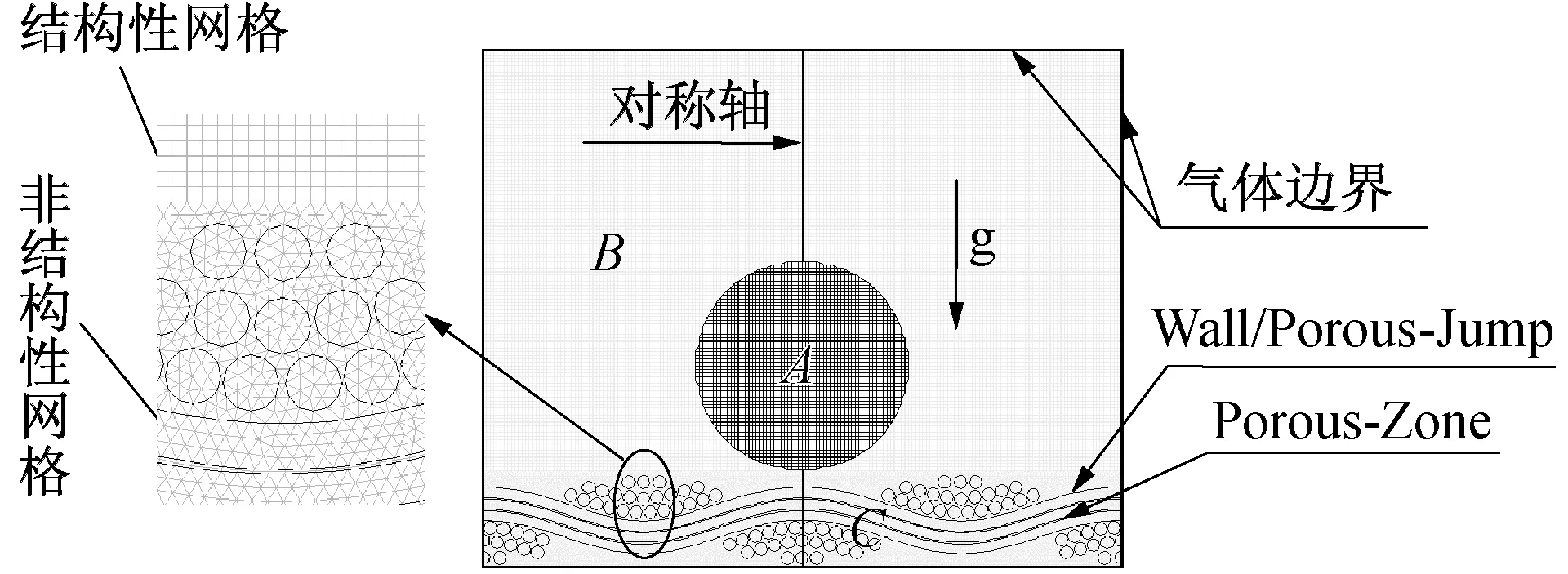
圖7 計算區域網格劃分及邊界條件Fig.7 Grid of calculation area and boundary conditions

3.3 定解條件設置

由于金屬鹽和還原劑溶液均為水基溶液，其打印沉積過程與水相似，故本文以水微滴為研究對象，其物性參數如表2所示.

表2 水微滴物性參數

采用有限體積法對控制方程進行離散，壓力速度的耦合采用PISO算法，壓力求解采用PRESTO！方法，連續方程和動量方程采用二階隱式格式求解，對時間一階離散. 計算單元液相體積分數采用CICSAM方法離散求解，控制方程采用QUICK格式進行離散以減少假擴散提高精度，時間步長為Δt=5×10-7s， Δt內迭代次數為20，殘差小于10-3，滿足迭代收斂要求.

4 模擬結果及試驗驗證

微滴在織物表面沉積過程主要為微滴在織物表面的碰撞以及在織物內的滲透過程. 液體能不能潤濕表面進而發生鋪展取決于鋪展系數SL/SG

SL/SG=σSG-σSL-σL

(24)

式中：σSG，σSL，σL為固-氣界面、固-液界面、液-氣界面的表面能.

當SL/SG>0時，液滴會完全潤濕基質并且鋪展為一層薄膜. 當微滴沉積在織物表面與其碰撞后首先主要沿徑向鋪展在織物表面，只有很少一部分液體會滲透到織物內部(本文模擬忽略此部分液體)，達到一個相對穩定的狀態后，此后微滴繼續滲透到織物內部[14-15].為了對沉積過程進行更深入細致的研究，把微滴在織物表面的沉積分為碰撞和滲透兩個過程分別進行研究[16].

4.1 碰撞過程

微滴與織物表面的碰撞過程與在普通固體基板表面的碰撞過程相似[3]，多孔區域的邊界條件采用Wall.設定微滴與基板的接觸角為98°，織物孔隙率為15.8%，滲透率為480.7 D.碰撞過程試驗采用筆者課題組自主開發的氣壓驅動式微滴噴射系統[2]，以機織平紋布為基板，通過調節控制參數實現微滴按需噴射，利用奧林巴斯i-speeds高速圖像攝影系統對微滴與織物表面碰撞過程及滲透過程進行采集，得到微滴碰撞各階段形態變化模擬結果與試驗照片如圖8所示，其中，上圖為試驗照片，下圖為模擬結果.

圖8 微滴碰撞過程模擬結果與試驗照片對比Fig.8 Comparison of simulation results and experimental pictures in the droplet impact process

通過圖8可看出，微滴與織物表面碰撞過程中，模擬結果與試驗觀測到各個階段微滴的形態均吻合較好. 微滴與織物表面的碰撞過程經歷了運動、射流、回縮階段、隨后振蕩沉積直到平衡. 其射流和鋪展階段在0.9 ms時間內完成，微滴鋪展達到最大直徑的時刻為0.9 ms，此時微滴為類餅狀. 隨后進入回縮階段，當運動到2.5 ms時，微滴第一次達到最大程度回縮位置. 此后經歷鋪展-回縮往復循環，直至能量完全消耗，最終約在34.9 ms時達到平衡狀態.

4.2 滲透過程

滲透過程多孔區域的邊界條件采用Porous Jump. 圖9為微滴滲透過程模擬結果與試驗照片，其中，上圖為試驗照片，下圖為模擬結果.

圖9 微滴滲透過程模擬結果與試驗照片對比Fig.9 Comparison of simulation results and experimental pictures in the droplet permeation process

由圖9可以看出，微滴沉積到織物表面后，隨著時間的延續其在織物表面的形態不斷發生變化，停留于織物表面液體體積在不斷減少，最終完全滲入織物中. 微滴在織物內部滲透初期，滲透速度非常快. 為分析微滴滲透速率加快的原因，提取微滴在24 ms時刻的壓力云圖如圖10所示.

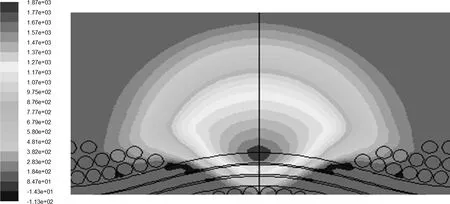
圖10 24 ms時刻微滴壓力云圖Fig.10 Droplet pressure cloud diagram at 24 ms

由圖10可看出，微滴內部壓力分布不均，梯度較大，上部為低壓區，微滴與織物接觸區域為高壓區，從上向下壓力越來越大. 這是由于微滴滲入織物內會產生毛細力的作用，導致毛細壓差的產生，從而使液體自發地在毛細孔隙中流動，開始階段毛細壓差大，織物中的孔隙順暢，液體滲入快，孔隙不斷地被液體所填充，出現快速芯吸現象，這與文獻[17]中的描述相吻合. 隨著壓差的減小，微滴的滲透速率逐漸減小，使得滲透過程減緩，直至液體完全滲入織物內部，達到穩定狀態.

由圖8和9的模擬結果與試驗照片對比可知，微滴與織物表面碰撞、鋪展及滲透直至穩定狀態的整個過程中，模擬結果與試驗觀測到各個階段微滴的形態均吻合較好，且從模擬的結果可以非常清楚的看到液滴在織物內部的滲透過程，表明模擬結果符合實際情況，證明了本文所提出的建模方法可行，為后續液滴在織物表面沉積過程的進一步研究奠定了基礎.

5 結 論

(1) 依據最小勢能原理建立了織物單胞的幾何模型，將紗線的受力與其幾何形態聯系起來，得到與實際織物結構相吻合的模型；

(2) 微滴在織物內部滲透初期，由于毛細壓差的作用使其滲透速率加快，出現快速芯吸現象；

(3) 微滴與織物表面碰撞、滲透過程的模擬結果與試驗結果吻合良好，表明提出的建模方法是合理可行的，為研究微滴的精確沉積奠定了基礎.

[1] KIEKENS P， JAYARAMAN S. Intelligent textiles and clothing for ballistic and NBC protection： Technology at the cutting edge [M]. Croatia Springer， 2012：119-136.

[2] 肖淵，黃亞超，蔣龍，等.噴射打印和化學沉積成形微細電路中微滴可控噴射研究[J].中國機械工程，2015，26(13)：1806-1810.

[3] 曾祥輝，齊樂華，蔣小珊，等.金屬熔滴與基板碰撞變形的數值模擬[J].哈爾濱工業大學學報，2011，43(3)：70-74.

[4] LI H J， WANG P Y， QI L H， et al. 3D numerical simulation of successive deposition of uniform molten Al droplets on a moving substrate and experimental validation[J]. Computational Materials Science， 2012， 65(4)： 291-301.

[5] LI H P， LI H J， QI L H， et al. Simulation on deposition and solidification processes of 7075 Al alloy droplets in 3D printing technology[J]. Transactions of Nonferrous Metals Society of China， 2014， 24(6)： 1836-1843.

[6] BUSSMANN M， CHANDRA S， MOSTAGHIMI J. Modeling the splashing of a droplet impacting a solid surface[J]. Phys Fluids， 2000， 12(12)：3121-3132.

[7] 李素麗，劉偉，賈寶勤.金屬沉積成形流固耦合工藝參數[J].江蘇大學學報，2015，36(5)：588-592.

[8] VERLEYE B， LOMOV S V， LONG A. Permeability prediction for themeso-macro coupling in the simulation of the impregnation stage of resin transfer moulding[J]. Composites： Part A， 2010， 41(1)： 29-35.

[9] CHEN Z R， Ye L， LU M. Permeability predictions for woven fabric preforms[J]. Journal of Composite Materials， 2010， 44(13)：1569-1586.

[10] 戴福洪，張博明，杜善義.用均勻化方法預報平紋織物的滲透率[J].復合材料學報，2009，26(2)：90-93.

[11] 于偉東，王錦成.纖維分布和混紡比對毛滌混紡紗毛型感的影響[J].東華大學學報(自然科學版)，2001，27(1)：24-28.

[12] 邰文峰，徐鑫華，宮菡菡.混紡紗線中纖維的分布測試探討[J].現代紡織技術，2010，26(1)：42-45.

[13] MARTIN S. Geometric and mechanical modelling of textiles[D]. Nottingham：The University of Nottingham， 2007.

[14] GOLPAYGAN A， HSU N， ASHGRIZ N. Numerical investigation of impact and penetration of a droplet onto a porous substrate[J]. Journal of Porous Media， 2008， 11(4)：323-341.

[15] EDIN B， Numerical simulations of flow due to drop impact on a porous substrate using a permeable wall model[C]//19h International Research/Expert Conference.2015:22-23.

[16] 劉曉娜.噴墨印刷在織物上的應用研究——薄織物上墨滴鋪展與滲透理論模型[D].無錫：江南大學紡織學院，2011.

[17] 范菲，齊宏進.織物孔徑特性與織物結構及芯吸性能的關系[J].紡織學報，2007，28(7)：38-41.

(責任編輯：杜 佳)

Research on the Deposition of Micro-droplet by Modeling Its Impacting Process on the Fabric Surface

XIAOYuan，SHENSong，ZHANGJingrui，LIUJinling，WUShan，YANGPengcheng

(College of Mechanical and Electrical Engineering，Xi’an Polytechnic University， Xi’an 710048， China)

To clarify the mechanism of droplets impacting the fabric surface and then their spreading and penetration process， a yarn centerline model is obtained based on the principle of minimum potential energy. A two-dimensional geometric model of the unit cell of the fabric is established by studying the distribution of the fibers in the yarn cross-section and the calculation method of the fiber volume fraction. Based on the fabric model built above， a two-phase flow model for a single droplet depositing and then deforming on the fabric surface is developed based on the volume of fluid (VOF) method. Using the established model， the process of the droplet/ fabric substrate collision and penetration have been simulated and investigated. Results from the simulation and experiment are compared. The results show that the model can realize the simulation of the colliding of droplets with fabric substrate and the penetration process. Result of the whole process is in good agreement with the experimental results. The method and results of the research can provide a foundation for the subsequent study on the influence of process parameters on the process of droplet deposition on the fabric surface.

fabric； modeling； fiber distribution； droplet； deposition; collision; penetration

1671-0444 (2017)03-0352-07

2016-09-02

國家自然科學基金資助項目(51475350)；西安工程大學學科建設經費資助

肖 淵(1975—)，男，陜西咸陽人，副教授，博士，研究方向為微制造系統與機電控制技術.Email: xiaoyuanjidian@xpu.edu.cn

TH 16

A