基于模糊失效概率的輸氣站場收球區定量風險評價研究

李平，張錦偉，稅旭東

1.中國石化川氣東送天然氣管道有限公司（湖北武漢430020）2.中國市政工程西南設計研究總院有限公司燃氣熱力設計研究院（四川成都610081）

基于模糊失效概率的輸氣站場收球區定量風險評價研究

李平1，張錦偉2，稅旭東1

1.中國石化川氣東送天然氣管道有限公司（湖北武漢430020）2.中國市政工程西南設計研究總院有限公司燃氣熱力設計研究院（四川成都610081）

針對目前國內缺乏輸氣站場風險因素客觀失效概率的問題，提出采用模糊失效概率來確定輸氣站場風險因素的失效概率。該方法以專家判斷為基礎，采用模糊集理論將專家判斷結果轉化為模糊失效概率。以人員受傷面積作為失效后果評價指標，從而計算出風險值，并提出風險等級劃分方法。最后對達化輸氣站收球區進行風險評價，其評價結果與實際風險程度一致。

輸氣站場；風險區塊；定量風險評價；模糊失效概率；失效后果

目前站場風險評價較通用的方法有定性評價方法、半定量評價方法和定量評價方法[1-4]。定性和半定量評價方法主要是基于專家判斷的風險評價，帶有很強的主觀性；定量評價方法是基于客觀失效概率的風險評價方法，評價結果客觀，但目前國內輸氣站場缺乏完備的風險因素的失效概率。針對3種評價方法的特點，提出采用模糊失效概率來確定輸氣站場風險因素的失效概率。該方法以專家判斷為基礎，采用模糊集理論將專家判斷結果轉化為模糊失效概率。以達化輸氣站為例，首先將站場進行風險區塊劃分[5]，然后對各風險區塊進行風險評價。以收球區為典型風險區塊，對其進行定量風險評價，驗證提出的風險評價方法的正確性，對其余風險區塊的風險評價具有借鑒作用。

1 輸氣站場收球區失效故障樹分析

1.1 建立收球區失效故障樹

故障樹分析由美國貝爾電話研究所提出，以所研究的故障作為頂事件建立故障樹，分析其中間事件和基本原因事件，用邏輯關系將事件連接，該方法能深入地揭示可能造成事故的各種因素。結合達化輸氣站收球區實際情況，建立了收球區失效故障樹，如圖1所示，其中收球區失效底層事件符號說明見表1。

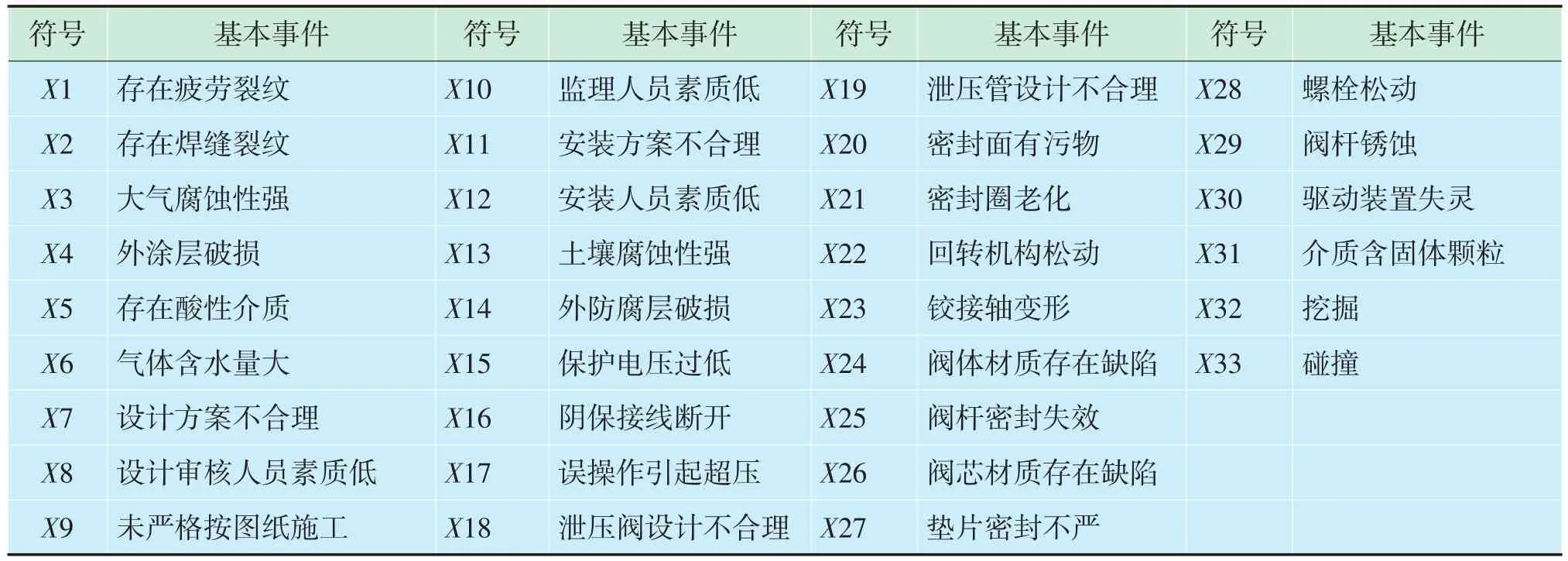
表1 收球區失效底層事件符號說明

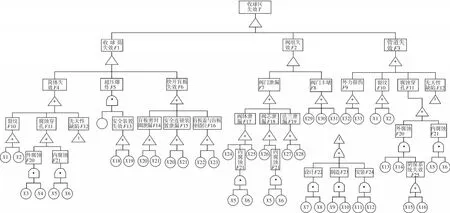
圖1 收球區失效故障樹

1.2 故障樹最小割集

故障樹最小割集是指導致故障樹頂事件發生的最小原因事件的集合。利用布爾運算原理，可將收球區失效故障樹轉化成最小割集的布爾代數方程：

T=X1+X2+X3X4+X5X6+X7X8+X9X10+X11X12+X13X14(X15+X16)+X17(X18+X19)+

2 輸氣站場收球區定量風險評價

首先對專家個人能力進行權重賦值，再將專家判斷評語轉化為模糊數，從而計算出故障樹底層事件的模糊失效概率[6]，再根據故障樹的邏輯關系計算出頂層事件失效的概率值。失效后果分析采用API 581的計算方法，以人員受傷面積作為評價指標，由模糊失效概率與失效后果計算風險值，從而確定風險等級。

2.1 模糊失效概率計算

2.1.1 專家權重的確定

采用參考文獻[7]中確定專家權重的方法，根據專家情況，采用強制比較法對其進行賦值，并求出各位專家的重要度權重。

2.1.2 計算平均模糊數

由于專家不可能準確估計出原因節點的概率，所以采用自然語言進行評判，自然語言分類越細，則專家評判結果與實際情況越接近，但并不意味著分類越細越好，過細的分類會使專家難以判斷。因此，本文設定“很小（VL）、小（L）、較小（FL）、中等（M）、較大（FH）、大（H）、很大（VH）”7個判斷等級，以三角形或梯形模糊數代替上述自然語言，如圖2所示。三角形模糊數表示為A=（a，b，c），其隸屬度函數[8]為：

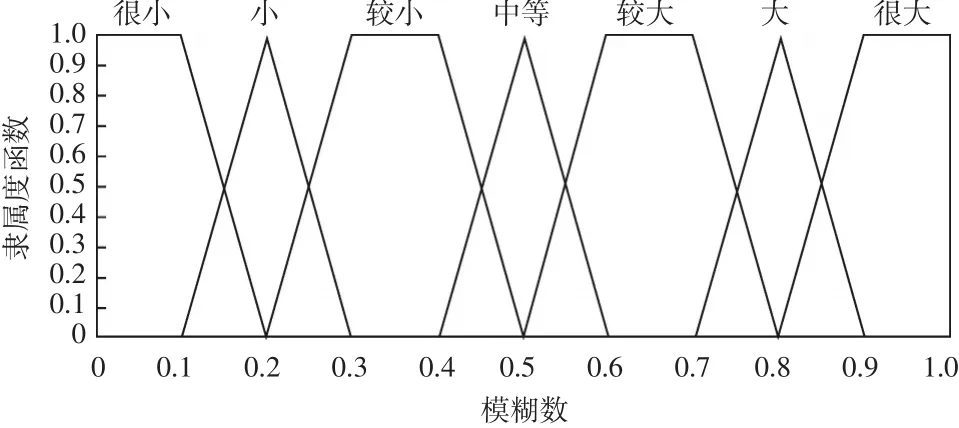
圖2 代表自然語言的模糊數

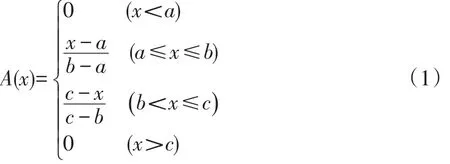
梯形模糊數表示為A=（a，b，c,d），隸屬函數為：

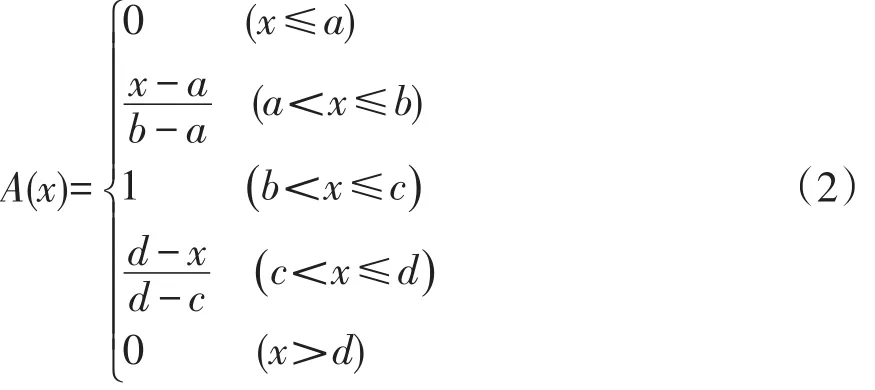
式中：a，b，c，d分別為模糊數的上下限。

專家對收球區故障樹中底層事件發生的可能性做出主觀判斷。在確定底事件發生概率時經常使用“德爾菲”方法，即要求多名專家分多輪估計底事件發生概率，這時就要對多個專家估計進行合成，常用的方法是選用模糊集的λ截集和加權平均值的方法組合不同的專家意見。根據模糊集截集的定義，λ截集為[0,1]上的閉區間[8]，λ截集見表2。

根據區間數的運算法則[9]，求專家評估意見的加權平均模糊數的關系函數。

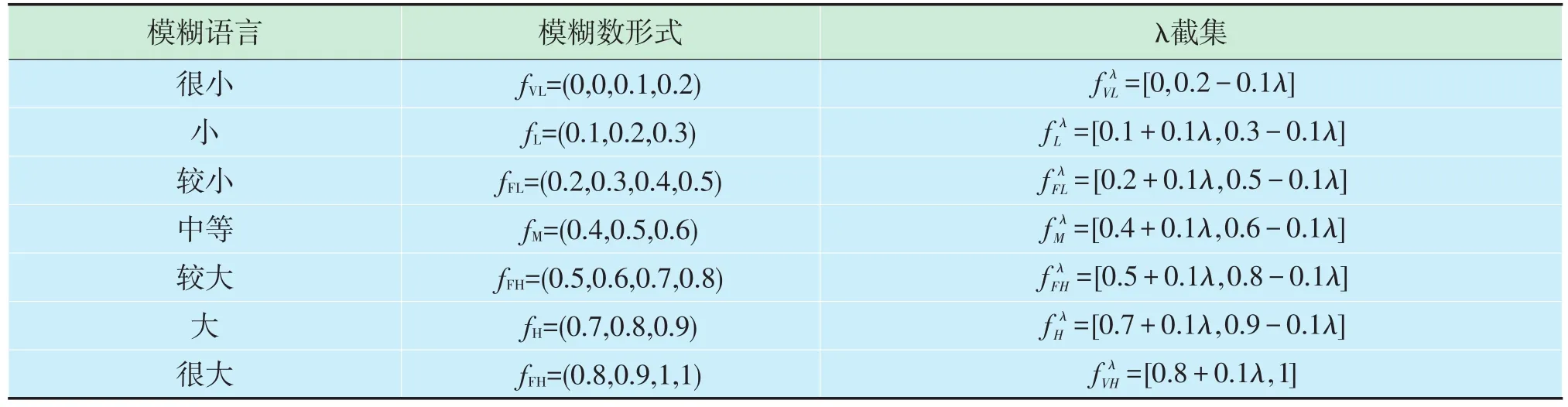
表2 模糊數形式與λ截集

例如，5位專家對站場收球區失效的底層基本事件“存在疲勞裂紋X1”各自進行了一輪估計，結果分別為“小、較小、小、很小、較小”，根據各專家知識層次和實際經驗的不同，可認為各專家具有不同的“置信度”。采用參考文獻[7]中確定專家權重的方法，根據專家情況，采用強制比較法對其進行賦值，得到各專家權重情況：W1=0.201 3、W2=0.198 2、W3= 0.215 6、W4=0.195 3、W5=0.189 6。根據模糊集截集的定義，“小、較小、小、很小、較小”的λ截集為[0,1]上的閉區間，依次為：A1==[0.1+0.1λ，0.3-0.1λ]、A2==[0.2+0.1λ，0.5-0.1λ]、A3==[0.1+0.1λ，0.3-0.1λ]、A4==[0，0.2-0.1λ]、A5==[0.2+0.1λ，0.5-0.1λ]，其中A1=A3，A2=A5,。實數上的閉區間稱為區間數，是一類特殊的模糊數，區間數之間的四則運算法則如下：

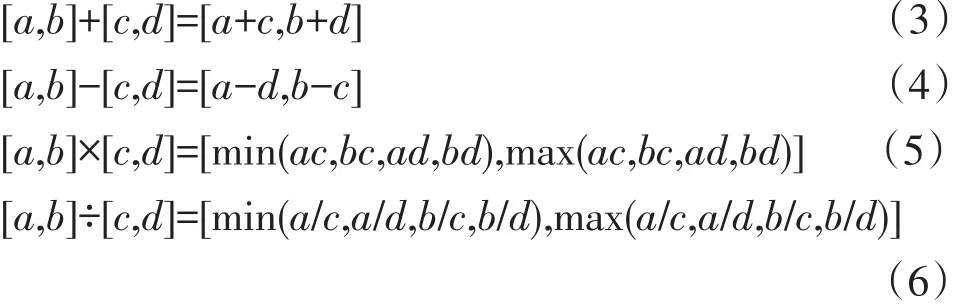
設Wλ為專家加權平均估計模糊數，根據區間數的運算法則有：

根據模糊集擴展理論知，Wλ也是模糊集。

令Wλ=[x1,x2]=[0.08047λ+0.11925,-0.1λ+0.35803],則可得到：和，所以平均模糊數的關系函數為：

2.1.3 將模糊數轉化為模糊可能性值FPS

采用Lin C.T和Wang M.J.提出的左右模糊數排序法[10]，將模糊數轉化為模糊可能性值。此方法定義的最大模糊集和最小模糊集分別是：

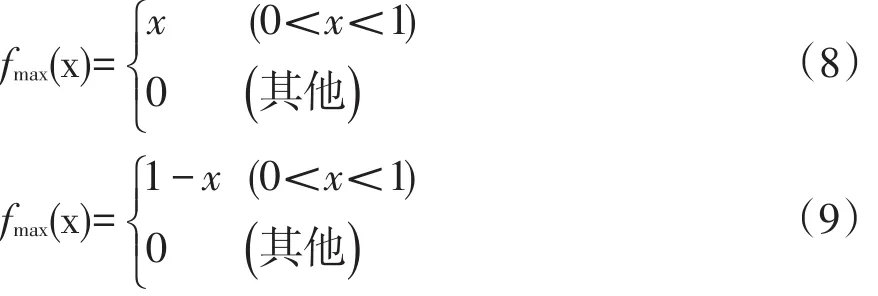
則模糊數W左右模糊的模糊可能性值為：

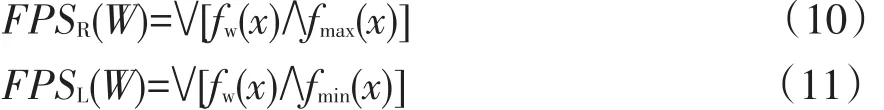
式中：fw(x)為模糊數W所對應的隸屬函數；W為對應失效可能性等級的模糊數；“∨”和“∧”分別表示取大和取小。

計算W的模糊可能性值：

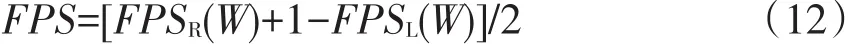
2.1.4 將模糊可能性值轉化為模糊失效概率FFR

根據參考文獻[10]，將模糊可能性值轉化為模糊失效概率，轉化公式如下：

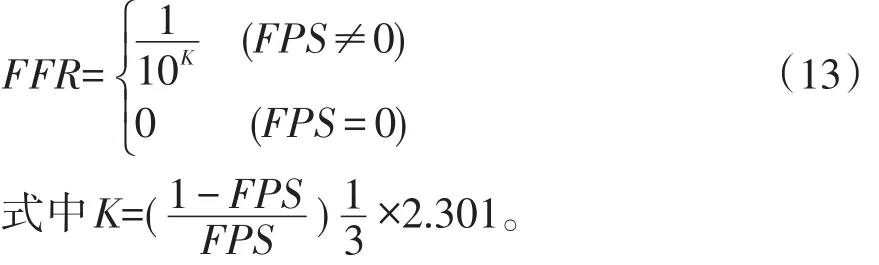
2.1.5 計算收球區頂事件模糊失效概率

假設各失效風險因素相互獨立，利用風險區塊失效故障樹最小割集的布爾代數方程，可以計算出收球區頂事件模糊失效概率，具體計算見式（14）。

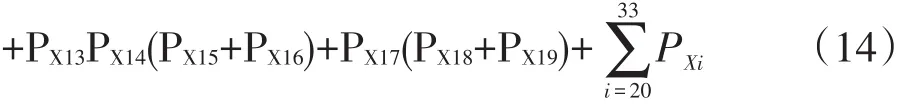
2.2 失效后果分析

失效后果分析采用API 581的計算方法。本文以設備和管道破裂、瞬時泄漏作為失效后果計算的前提條件。

2.2.1 氣體泄漏速率計算r

1）當P/P0≥((r+1)/2)r-1時，氣體泄漏速率計算公式見式（15）[11]：

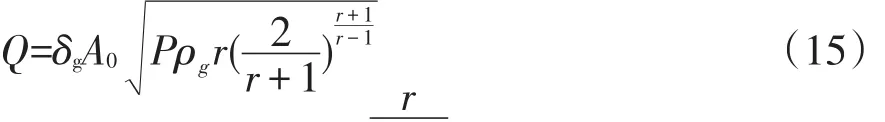
2）當P/P0＜((r+1)/2)r-1時，氣體泄漏速率計算公式見式（16）：

式中：Q為氣體泄漏速率，kg/s；P為容器內介質壓力，Pa；P0為大氣壓力，Pa；r為熱容比，取1.33；δg為氣體泄漏系數，當裂口形狀為圓形時取1.00，三角形時取0.95，長方形時取0.90；A0為裂口面積，m2；ρg為容器內氣體密度，kg/m3；M為氣體相對分子質量；Z為天然氣壓縮系數；T為介質溫度，K。

2.2.2 失效后果計算

本文采用人員受傷面積作為后果評價指標[12]，借鑒API 581瞬時泄漏不自動點火人員受傷面積CA的計算方法，見式（17）。

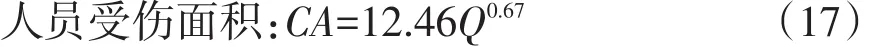
2.3 定量風險計算

收球區的風險值由模糊失效概率與失效后果相乘進行計算見式（18）：

2.4 風險等級劃分

借鑒參考文獻[13]中對川氣東送典型站場失效概率的等級劃分，并結合達化輸氣站收球區的實際情況，對收球區失效概率進行等級劃分，從而由公式（18）可計算出收球區失效風險等級劃分區間。收球區風險等級劃分及其意義見表3。

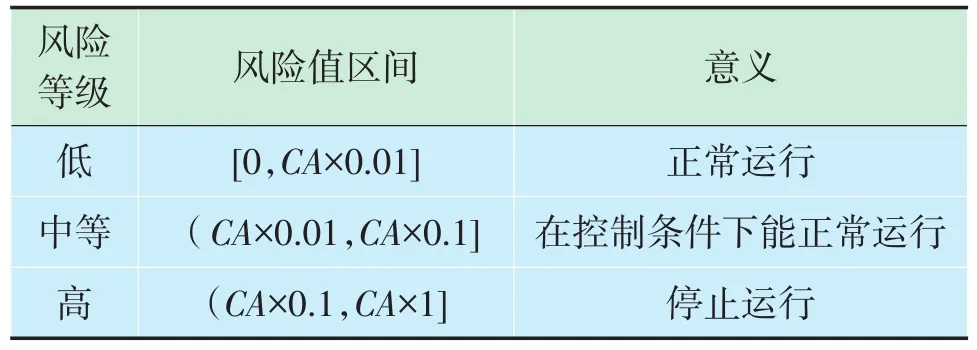
表3 收球區風險等級劃分及其意義

3 實例分析

以達化輸氣站收球區為例，進行風險區塊定量風險評價。目前，該輸氣站的輸送氣量為290× 104Nm3/d，進站壓力為6.0 MPa，出站壓力：去川投燃氣為4.2 MPa、去潤發門站為4.4 MPa、去CNG加氣母站為4.0 MPa，介質溫度15℃。

3.1 模糊失效概率計算

1）專家權重的確定。采用參考文獻[7]中確定專家權重的方法，根據專家情況，采用強制比較法對其進行賦值，得到各專家權重情況：專家A權重0.201 3，專家B權重0.198 2，專家C權重0.215 6，專家D權重0.195 3，專家E權重0.189 6。

2）計算平均模糊數。5位專家對收球區失效的底層基本事件“存在疲勞裂紋X1”發生的可能性做出主觀判斷，結果分別為“小、較小、小、很小、較小”。采用λ截集對專家自然語言進行綜合處理，“較小、小、很小”的λ截集見表2。根據2.1節，式（7）即為平均模糊數的關系函數。

3）將模糊數轉化為模糊可能性值FPS。由式（7）～式（11）可得模糊數W左右模糊的模糊可能性值分別為：FPSR(W)=0.129 7，FPSL(W)=0.765 4。由式（12）得W的模糊可能性值FPS=0.182 2。

4）將模糊可能性值轉化為模糊失效率FFR。根據式（13），計算得，K=3.795 6，FFR=1.60×10-4，即“存在疲勞裂紋X1”為1.60×10-4。

同理，可以算出其他底層基本事件的模糊失效概率FFR，見表4。

最后，利用公式（14）便可以算出達化輸氣站收球區的模糊失效概率為3.55×10-3。

3.2 失效后果計算

在安全措施的保護及站場應急反應下泄漏持續時間通常不超過5 min，因此以泄漏時間5 min來進行收球區失效后果的計算。由于P/P0≥1.85，故利用公式（15）可以算出Q=56.7 kg/s。從而由公式（17）可以算出CA=6 046 m2。

3.3 風險值計算

由表3可知，收球區風險等級劃分見表5。

由公式（18）可以算得收球區的風險值R= 3.03。由表5可知，收球區的風險等級為低。評價結果與現場收球區實際風險程度一致。

4 結論

1）采用模糊失效概率來確定輸氣站場風險因素的失效概率，解決了輸氣站場因缺乏風險因素的客觀失效概率而無法進行定量風險評價的難題。

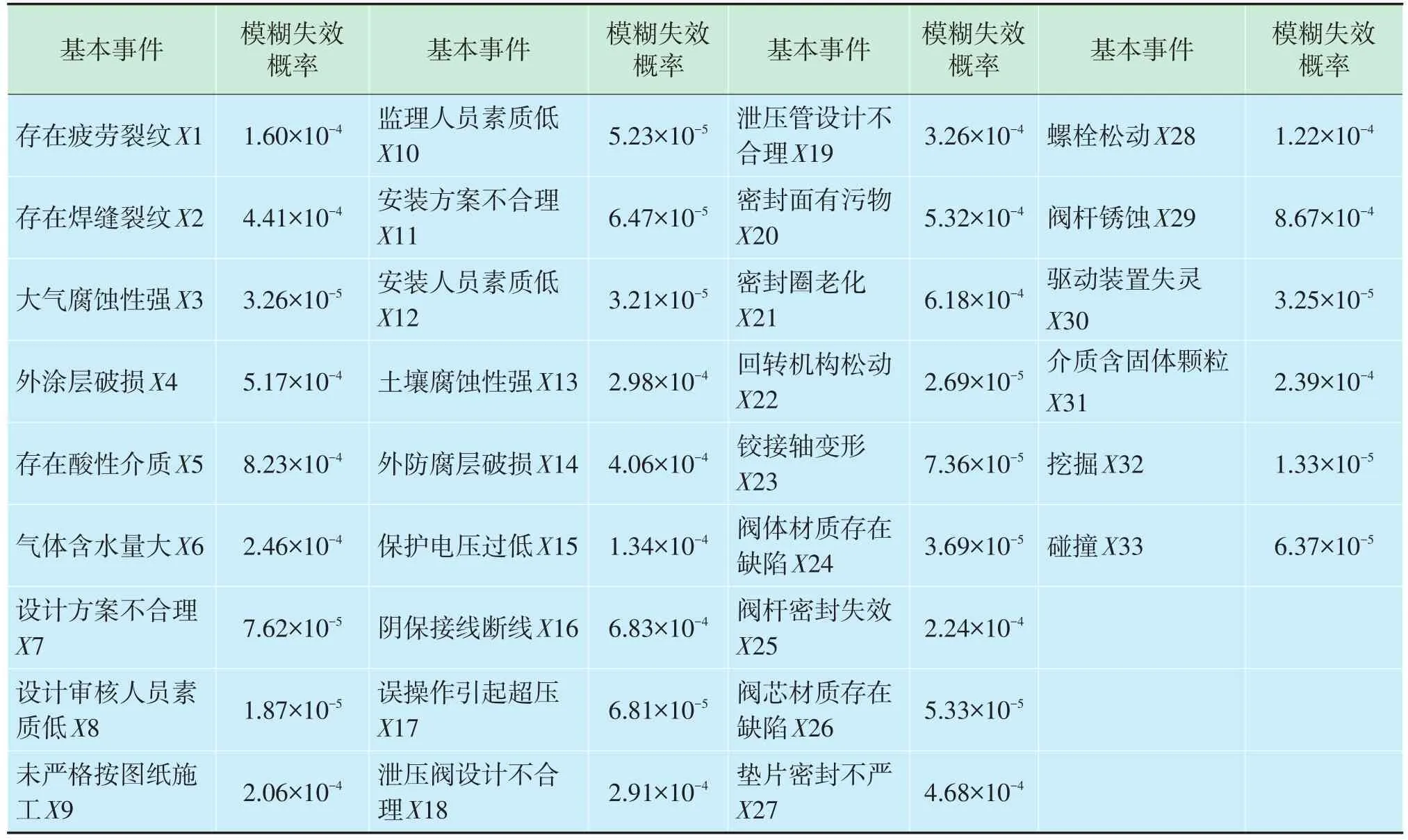
表4 基本事件模糊失效概率表

表5 收球區風險等級劃分

2）通過對達化輸氣站收球區的風險評價表明，筆者提出的定量風險評價方法具有一定的實際可操作性，同時對輸氣站場其他功能區塊的風險評價也有一定的借鑒意義。

[1]王婷,項小強,戴聯雙,等.輸油氣站場HAZOP分析方法及其應用[J].天然氣工業,2011,31(10)：97-100.

[2]施林園,鄭潔,李晶.四川輸氣站場風險評價研究[J].天然氣工業,2004,24(11)：135-138.

[3]馮文興,稅碧垣,李保吉,等.定量風險評價在成品油管道站場的應用[J].油氣儲運,2009,28(10)：10-13.

[4]馮文興,賈光明,項小強,等.原油管道站場的定量風險評價[J].油氣儲運,2012,31(3)：181-183.

[5]趙新好.輸氣站場設施風險評價技術研究[D].成都：西南石油大學,2012.

[6]謝云杰,姚安林,錢浩,等.海底管道系統失效可能性評價方法研究[J].中國海上油氣,2007,19(2)：134-137.

[7]樂叢歡,丁紅巖,董國海,等.基于模糊故障樹的海洋立管破壞失效風險分析[J].自然災害學報,2012,21(2)：173-179.

[8]朱云斌,黃曉明,常青,等.模糊故障樹分析方法在機場環境安全中的應用[J].國防科技大學學報,2009,31(6)：126-131.

[9]孫德青.液化石油氣球罐的可靠性管理研究[D].成都：西南石油大學,2007.

[10]Lin C.t.,Wang M.J.Hybrid fault tree analysis using fuzzy sets [J].Reliability Engineering and System Safety,1997,58(3)：205-213.

[11]陳國華.風險工程學[M].北京：國防工業出版社,2007.

[12]谷志華,帥健,董紹華.應用API 581對輸氣站進行定量風險評價[J].天然氣工業,2006,26(5)：111-114.

[13]廖柯熹，牛化昶，張學洪，等.川氣東送管道典型站場風險量化評價[J].天然氣與石油，2012，30（1）：5-9.

In view of the lack of objective failure probability of risk factors in gas transmission stations at present in China,it is proposed to determine the failure probability of risk factors in the gas stations using fuzzy failure probability.The method is based on expert judgment,and uses fuzzy set theory to transform the expert judgment result into fuzzy failure probability.Taking the injured area of personnel as the evaluation index of the failure consequence,the risk value is calculated and the risk grade division method is put forward.Finally, the risk of the receiving ball area of Dahua gas station is evaluated,and the evaluation result is consistent with the actual risk level.

natural gas station；risk block；quantitative risk assessment；fuzzy failure probability；failure consequence

王梅

2017-03-18

李平（1986-），女，碩士，主要從事油氣長輸管道風險評價與完整性管理工作。