自然隨機溫度應力條件的加速退化模型研究

王彥霖，姚洪偉

（北京電子工程總體研究所，北京100854）

自然隨機溫度應力條件的加速退化模型研究

王彥霖1，姚洪偉2

（北京電子工程總體研究所，北京100854）

目的利用加速退化試驗對免維護導彈服役期進行分析評估，給出自然溫度環境應力等效處理方法和加速退化因子數學模型。方法對環境溫度實測數據進行統計處理，利用阿倫尼斯模型給出時域內的等效溫度均值函數，將隨機溫度應力轉換為溫度循環應力。利用基于統計數據的加速退化模型求得產品激活能，推導給出相對隨機溫度應力的加速退化因子數學模型。結果利用給定加速模型，定量給出了某產品在典型地區的服役期，評估結論符合預期。結論改進后加速模型綜合了自然環境隨機溫度應力對產品性能影響，能夠較好地對產品服役期進行評估。

服役期；加速退化因子；偽壽命分布

導彈在服役期間，一般要經歷運輸、庫房存放、戰備值班、訓練、維護不同的任務階段，經歷各種自然和誘發環境。除庫房存放期間溫度應力受控外，其他任務剖面主要受自然環境溫度影響。要在有限的時間內獲取彈上關鍵產品的服役壽命，必須采用加速退化試驗技術與壽命評估方法。相對于傳統加速壽命試驗，加速退化試驗（ADT）具有試驗時間短、加載應力集中、獲取產品信息量大等優勢，非常適合于具備性能退化規律的產品。

為分析自然溫度環境對產品性能參數退化的影響，文中完成了自然溫度隨機應力的等效模擬及ADT加速因子的模型研究，為開展加速試驗奠定基礎。

1 ADT基本理論

產品在長期使用和貯存過程中，其失效模式大都與產品潛在的性能退化過程緊密相關，可以認為產品發生失效（或故障）是產品性能退化的最終結果。如果產品性能退化速度非常緩慢，要在其實際使用環境下對裝備壽命或者關鍵產品的性能保持時間（注：針對免維護裝備）進行驗證并給出結論，所需要的時間較長，對研制和使用雙方來講都將難以接受。要解決這個問題，必須研究不同應力強度與產品性能退化速度的關系建立加速模型，進而可通過加速試驗，利用高應力下的退化數據推算產品在正常使用環境下的性能變化規律，最終達到對其使用壽命和性能保持時間進行評估的目的。這種利用產品在高應力水平下的性能退化數據預測和估計產品在實際環境下的可靠性及性能保持時間的加速試驗方法稱為加速退化試驗（ADT）。產品能夠進行ADT的前提是其必須具有一個或多個關鍵性能參數的可加速性，即性能特征參數具有隨應力產生規律性變化的特征。也就是說，產品在加速應力與實際應力下性能退化關系的加速因子模型應當是確定的，加速因子是唯一的。

由于導彈服役期間外界自然環境具有明顯的隨機特性，因此首先要對自然環境隨機應力進行適當的簡化和等效處理，才能具備開展ADT的必要條件，同時還應依據產品特點選擇適當的加速退化模型求得加速因子。加速退化模型[1]假設有以下幾條：加速應力與實際應力下的退化機理相同；退化過程不可逆；加速退化模型與退化機理對應關系唯一；不考慮加速試驗前的性能退化量。目前，加速退化模型一般分為基于物理或試驗的加速退化模型和基于統計數據的加速退化模型。

如果掌握產品的退化機理，可以選用基于物理或基于試驗的加速退化模型。這類模型中通常包含一些隨機變量參數，一般不具有解析形式的可靠性函數表達式。Carey[2]等利用基于物理或基于試驗的加速退化模型研究了集成邏輯系列(ILF)的可靠性，利用Arrhenius定理和極大似然方法，研究了產品退化量和絕對溫度之間的關系。相對而言，基于統計數據的加速退化模型在工程中應用較多。其實質是用統計模型來描述加速退化數據，通過給定的退化軌跡模型[3—4]和既定失效閾值，給出產品的偽壽命（產品性能退化至設計所允許閾值的時刻）變量，將加速退化數據轉化為加速壽命數據進行研究。該方法的核心是依據合理的統計信息或物理模型來確定退化軌跡函數。目前，基于退化軌跡進行性能可靠性推斷理論已經相對比較成熟。上官芝[5]研究了對偽失效數據應用非線性曲線擬合法進行分布假設檢驗，給出了退化軌跡模型和加速退化試驗數據的方法。莊東辰[6]研究了基于線性回歸模型的退化數據統計方法，對常應力和加速應力下的退化失效進行了探討。

盡管部分學者對采用多應力和步進應力作為加速應力開展ADT進行了一些研究，如汪亞順[7]研究了雙應力交叉步進加速退化試驗的方法，但目前工程應用還不是很普遍。考慮加速模型的復雜性和實際應用的便利，目前ADT在工程應用中加速應力較多選用單應力或恒定應力。

2 服役期自然環境應力的等效處理

2.1 裝備服役期環境條件特點

某型導彈服役期間，除在庫房存放外，其余大部分時間均暴露在自然環境中，所受環境應力的主要因素包括所在區域的地理環境和氣候環境。根據文獻[8]的研究，一個特定區域的地理環境一般具有穩定性，在相對比較長的時間內基本沒有明顯的變化，可以視為一個不變系統。其氣候環境則同時存在周期性和隨機性特點。其中，太陽系規律性的天體運動是一個地區氣候環境周期性的根本成因。氣候環境的隨機性表現在各種復雜因素所導致的氣候無規律變化。一個區域的自然溫度數據通常年平均溫度變化較小，不同年份中相同日期溫度往往呈現較大的隨機性。

2.2 自然環境溫度應力的等效模型

環境溫度數據的置信上限計算。考慮到氣候環境的周期性，如果取樣時間長度充分長，采集樣本量足夠多，理論上樣本數據能夠逐步接近該區域環境應力的總體統計特征。為利用加速退化試驗研究自然環境溫度應力下裝備性能參數變化規律，得到確定的加速因子模型，首先需要對裝備服役區域的歷史溫度數據進行統計分析處理，以反映隨機應力對產品的影響規律。肖敏[9]研究了自然環境實測數據的處理方法，利用不同日期相同時刻點的數據均值作為環境特征數據。均值法的處理結果受數據采集量大小影響較大，文中考慮不同年份日溫度的隨機性特點，在假設不同年份同一時刻溫度數據服從正態分布前提下，對數據進行統計處理給出各時刻點溫度特征值。根據正態數據的無方向性檢驗要求[10]，至少應以采集到的某服役地區m年（m≥3）之內的溫度應力作為研究對象。為增大溫度樣本數量，以更準確地反映自然環境應力的總體特征，將m年內以小時為單位采集的溫度數據作為該服役區域的自然環境溫度應力樣本。

在假定所采集溫度數據準確的前提下，設日采集溫度數據個數為n，記裝備服役地域m年內自然環境溫度數據樣本矩陣為T[m][365][n]。為分析樣本的統計特征，按照順序統計量法[11]，將m年相同日期內同一時刻的樣本觀測值：t1，t2，…，tm按照由小到大的順序排列，滿足T（1）≤T（2）≤…≤T（m），得到該時刻自然溫度數據總體中位數的估計值：

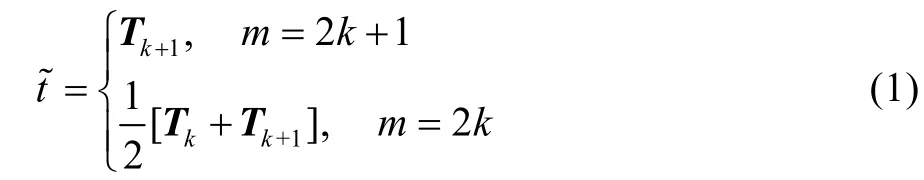
求得樣本極差ΔT=T(m)－T(1)，則某地不同年份同一日期同一時刻溫度數據總體T的標準差σ可取：

在進行數據統計分析時，希望所得的統計估計量能夠較好地反映各個年份溫度變化，同時又不希望統計估計量過大。因此，記給定置信度β的正態分布分位點的分位數為Zβ，則某時刻環境溫度單側置信上限Tβ為：

將Tβ作為該時刻環境溫度的理論數據。通過上述處理，則獲取到一年中以小時為基準的溫度數據，并且包含了該地域溫度變化的統計特征。根據實際數據獲取情況，也可取較長間隔期的樣本數據按照上述方法進行處理，并獲得溫度包絡區間。

環境應力的等效溫循應力剖面。從宏觀上看，產品性能退化可以歸結到產品所用材料和元器件的性能變化。從微觀上看，產品性能退化的根本原因是外界作用導致的原子、分子變化。這種微觀變化的長期、累積效應逐漸反映到材料、元件的改變。當材料、元件性能變化達到一定程度，產品的失效即隨之發生。工程中的大部分退化失效均符合這種失效過程。根據阿倫尼烏斯理論，反應速度K與溫度的關系服從Arrhenius方程。

式中：Kt為t時刻的退化速度（反應速度）；A為比例常數，又稱頻數因子；ΔE為激活能；R是玻爾滋曼常數，R=8.617×10－5eV/K；T為絕對溫度，是時間t的函數。

為了通過加速退化試驗去研究產品在自然環境應力下的性能變化規律，首先需將隨機自然環境應力轉化為具有確定數學解析關系的等效應力，等效的基本原則是相同時間內產品在等效應力和實際自然環境溫度應力下產生相同的性能累計變化量。選取產品的溫度應力敏感參量，在不考慮試驗開始前既有退化量的前提下，則（0，t）時間內的該參量的累計退化量ht應為退化速度的積分：

為便于研究退化速度與絕對溫度應力兩者之間的關系，工程上通常將式（4）阿侖尼烏斯方程通過數學變換為式（6）形式，即：

式中：a，b為待定常數；T為產品所受的絕對溫度應力。并有：

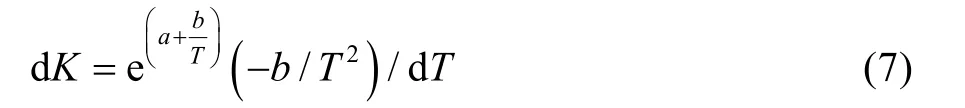
當試驗溫度應力為隨時間變化的變量時，在作用時間（t1，t2）內，溫度應力給產品帶來的累計退化量為：

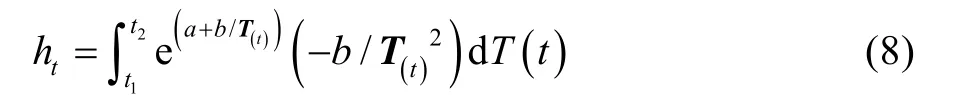
根據積分中值定理，有：

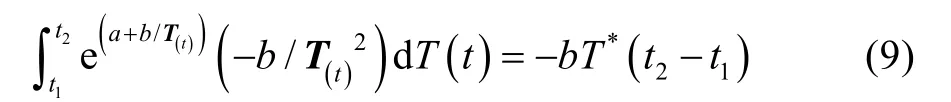
進而得到（t1，t2）之內溫度應力的等效均值函數T*：

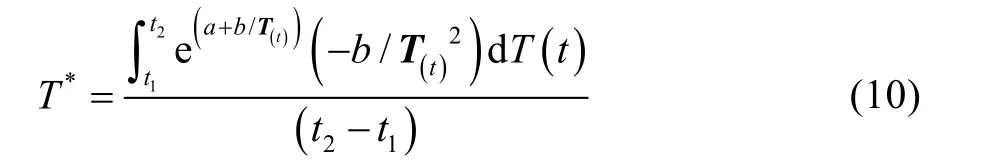
為反映一年內溫度循環變化的情況，將經過上述統計處理后的一定時域內的N個數據按照順序統計量法進行處理，得到年溫度數據的中位數t*。以年溫度數據中位數作為基準溫度，將溫度數據劃分為兩個集合{tL}和{tH}。

分別針對數據集合{TL}和{TH}按照式（10）處理，將高于中位數的數據折合為等效高溫數據，將低于中位數的數據折合成等效低溫數據，得到等效的溫度循環剖面的上限和下限溫度，其差值為等效循環溫度剖面溫度循環幅值。溫度上限時間和溫度下限時間按照相應溫度集合在全年中的累計時間總數進行計算。處理后，即得到了該型導彈所在服役區自然環境溫度應力的基于累計退化量相等的等效溫度循環應力剖面，如圖1所示。

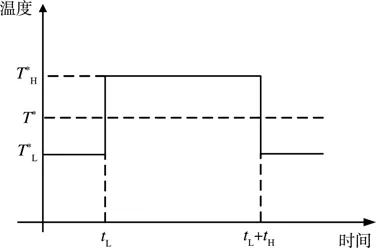
圖1 等效溫度循環應力剖面

3 自然環境ADT加速因子模型研究

通過上述對自然環境觀測溫度處理的過程，將服役期自然環境的周期性和隨機性的溫度應力利用數據統計處理方法和阿倫尼斯方程等效轉化為溫度循環應力。因此，免維護裝備的服役期壽命問題即可以轉化為研究彈上典型產品在加速應力與等效循環應力剖面的加速退化因子問題。

加速因子反映不同加速應力水平下，產品達到相同性能退化量所需試驗時間的關系。獲得同樣的試驗退化量，加速因子越大，試驗時間越短。加速因子是不同試驗應力水平下試驗數據折算的核心。文獻[12]提出了加速退化試驗的加速退化因子定義如下：相同產品在t=0時，分別在不同的應力水平Si，Sj下開展性能退化試驗，在某個t＞0時刻其特征值退化量hi(t)，hj(t)之比定義為加速退化因子，簡稱加速因子。

根據加速因子定義，在加速退化試驗中必須同時記錄試驗時間和該時刻的性能退化量。目前，加速退化試驗采用的應力一般分為恒定應力、步進應力和序進應力三種方式。這里僅對恒定應力與溫度循環應力的加速因子進行分析。通過坐標平移，并考慮升溫降溫速率，將圖1等效溫度循環簡化成圖2所示。其中T0為溫度應力位于高溫和低溫之間的初始值，代表試驗初始環境溫度，T0值可取年溫度數據的中位數t*。在（0，t1）和（t5，t6）期間，產品受到逐步升高的溫度應力影響。在（t2，t4）期間，產品受到逐步降低的溫度應力影響。（t1，t2）期間為恒定高溫應力，（t4，t5）為恒定低溫應力。TU和TL分別代表試驗高、低溫極限。

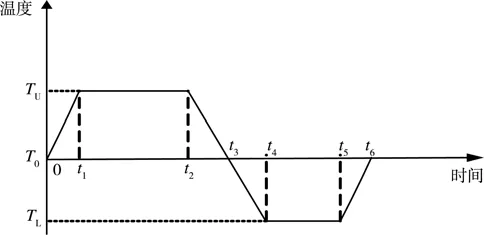
圖2 簡化溫度循環應力剖面

為便于分析，將升溫和降溫曲線視為線性函數，則圖2溫度與時間的關系可表示為函數關系：

式中：α，β為曲線的形狀參數。

根據Arrhenius模型，由式（4）、（12）、（13）可知，在等效溫度循環應力Tb條件下，相對試驗初始環境溫度應力T0的平均等效加速因子為：

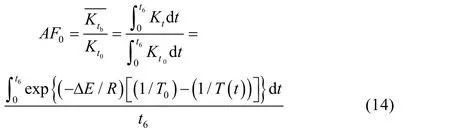
為縮短試驗時間，可以根據需要選取能夠獲得更高退化速率的加速應力Ta。姜仁元[13]研究了不同溫度應力下功能退化型加速壽命試驗加速系數推導。根據Arrhenius模型，加速應力Ta相對初始環境溫度T0，有加速因子A F1如下：

由上述溫度循環應力剖面與自然環境溫度應力的等效轉化過程和式（12）加速退化因子定義，加速退化試驗應力Ta相對自然環境等效循環應力的加速因子AF可表示為：

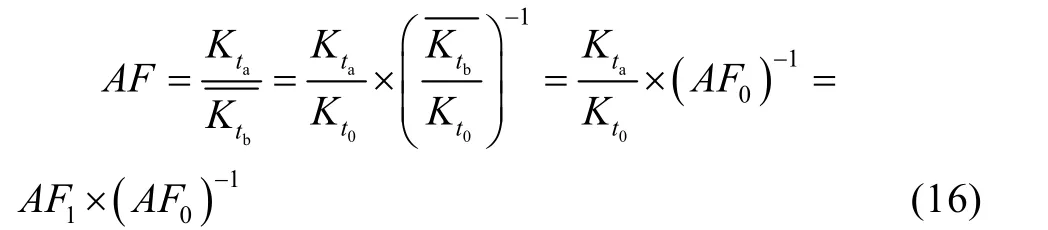
從上述推導過程知，為求得相對自然環境應力的加速系數，首先應獲知產品激活能ΔE。

文獻[14]中給出了利用最小二乘法求得激活能ΔE的公式推導。通過恒定應力加速退化試驗采集到不同應力條件下的產品性能退化觀測值，在假設產品性能退化量服從正態分布前提下，利用基于統計數據的ADT模型和極大似然法，首先求得產品性能退化速度均值μ和方差σ。由不同溫度條件下的退化量數據，根據式（4）Arrhenius方程，可得到激活能的數學模型式（17），其中i為觀測序數，n為應力水平水平數。

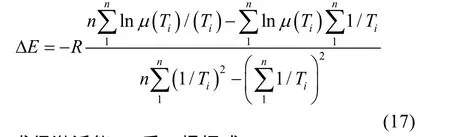
求得激活能ΔE后，根據式（14）、（15）、（16）即可以得出針對自然服役環境的等效加速退化因子。已知加速退化因子，免維護導彈自然環境條件下的服役期的評估問題，可以轉化為對彈上典型產品在雙恒定應力Ta，T0條件下的產品性能退化問題的研究。基于恒定應力的產品加速退化試驗目前已經有很多成熟的方法和理論。

4 模型應用示例

彈上某典型電子設備進行加速退化試驗，試驗樣品2個，每個樣品在3個溫度應力水平（333，348，363 K）下分別觀測6次。根據加速試驗結果，評估得到該產品在常溫25℃的下服役壽命為12年。

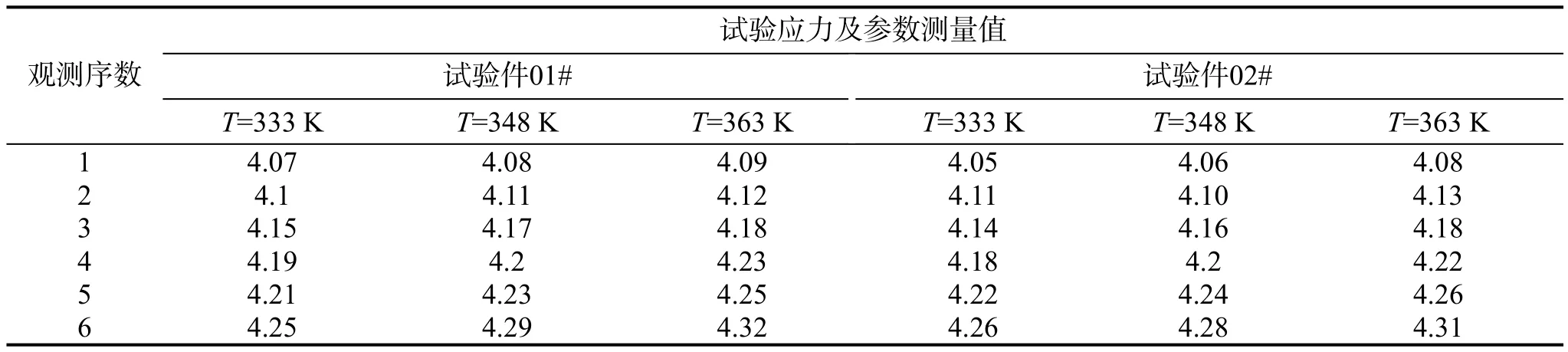
表1 某電子設備加速退化試驗性能參數測試數據

利用極大似然法，計算得到溫度應力水平333，348，363 K下的退化速度均值分別為2.6398×10-4，2.9503×10-4，3.2609×10-4。

計算可得到Arrhenius方程中的比例常數A=2.5258×10-3，等效均值函數中的待定系數：a=lnA=-5.9812，b=-734.9774，產品激活能ΔE=6.3333× 10-2eV。

下面利用上述加速模型，計算該產品分別在甘肅酒泉和某典型地域使用時的服役壽命。

1）酒泉地區服役。酒泉地區各月份溫度數據具體見表2。按照順序量統計方法，得到年溫度數據中位數為281.935 K（8.785℃），等效低溫數據為269.347 K（-3.903℃），等效高溫數據為288.818 K（15.668℃）。

表2 酒泉地區的月份溫度均值數據

按照上述加速模型，等效溫度循環應力相對初始溫度的加速因子為A F0=0.975，初始溫度相對常溫25℃（298.15 K）下的加速因子為A F1=0.868。根據常溫25℃（298.15 K）下服役壽命12 a，可計算出該裝備在酒泉地區使用時的服役壽命評估結果為14.5 a。

2）某典型地域服役。該典型地域各月份溫度數據見表3。年溫度數據中位數為300.15 K（27℃），等效低溫數據為292.1 K（18.95℃），等效高溫數據為294.729 K（21.579℃）。

表3 某典型地域各月份溫度均值數據

等效溫度循環應力相對初始溫度的加速因子為A F0=0.945，常溫25℃（298.15 K）下相對初始溫度的加速因子為A F1=0.984。根據常溫25℃（298.15 K）下服役壽命12 a，計算出該裝備在該典型地域使用時的服役壽命評估結果為12.4 a。

3）加速模型驗證。由于目前上述兩地裝備的在役年度較短，測試數據較少，尚無法對加速模型正確性進行充分驗證。兩地設備的性能參數退化量明顯不符合恒溫試驗條件退化規律，且酒泉地區裝備退化量相對較小，與上述壽命評估結論存在邏輯上的一致性，可以部分佐證改進加速模型的合理性及正確性。

相對按照25℃恒溫條件給出的產品加速壽命結論，新的加速模型得出的評估結論更能準確反映出不同區域實際自然環境條件對裝備服役期的影響。

5 結語

文中基于阿倫尼烏斯方程，給出了自然環境溫度應力的等效處理方法和時域內的等效溫度均值函數的公式推導。在恒加應力退化試驗基礎上，給出了相對自然環境等效溫度循環剖面的加速退化因子數學模型。盡管針對環境應力的等效處理方法還有改進的余地，但新的模型綜合考慮了常規加速數據與環境等效應力數據的融合處理，對利用加速退化試驗研究裝備在自然環境的服役期具有一定的參考作用。

參考文獻：

[1]鄧愛民,陳循,張春華,等.加速退化試驗技術綜述[J].兵工學報,2007,28(8):1002—1007.

[2]CAREY M B,KOENIG R H.Reliability Assessment Based on Accelerated Degradation:A Case Study[J]. IEEE Transactions on Reliabilit y,1991,40(5):499—506.

[3]馬小兵,王晉忠,趙宇.基于偽壽命分布的退化數據可靠性評估方法[J].系統工程與電子技術,2011,33(1): 228—232.

[4]鐘強暉,張志華,王磊.考慮模型選擇的退化數據分析方法[J].系統工程,2009,27(17):111—114.

[5]上官芝,付桂翠,萬博.基于加速性能退化的元器件貯存壽命預測[J].電子產品可靠性與環境試驗,2009, 27(5):32—36.

[6]莊東辰.退化失效模型及其統計分析[D].華東師范大學,1994.

[7]汪亞順,莫永強,張春華,等.雙應力步進加速退化試驗統計分析研究—模型與方法[J].兵工學報,2009, 30(4):451—456.

[8]張文偉,李宏民.自然貯存場自然環境剖面歸納處理[J].裝備環境工程,2011,8(1):61—65.

[9]肖敏,周漪,楊萬均.典型環境中三種自然環境加速試驗方法的環境強化效果分析[J].裝備環境工程,2014, 11(2):26—31.

[10]GB 4882—85,數據的統計處理和解釋正態性檢驗[S].

[11]潘吉安.可靠性維修性可用性評估手冊[M].北京:國防工業出版社,1995.

[12]趙建印,孫權,彭寶華,等.基于加速退化試驗數據的可靠性分析[J].電子質量,2005(7):30—33.

[13]姜仁元,張興唐,楊亦春.溫度應力下功能退化型加速壽命試驗問題研究[J].南京理工大學學報,2000,24(6): 523—527.

[14]袁立峰.基于加速退化的電子設備可靠性分析[J].電子產品可靠性與環境試驗,2009,27(3):38—41.

ADT Model under the Stress of Natural Random Temperature

WANG Yan-lin1,YAO Hong-wei2
(Beijing Institute of Electronic System Engineering,Beijing 100854,China)

ObjectiveTo analyze and evaluate the service time of maintenance-free missiles with the accelerated degradation experiment,give equivalent treatment method for stress of natural random temperature,and build a model of the accelerated degradation factors.MethodsThe statistical processing method was applied to treat environment temperature data.The Arrhenius model was adopted to draw the conclusion about the mean function of equivalent temperature in time domain.The random temperature was converted into the cycling stress of temperature.The accelerated degradation model based on statistics was applied to obtain the activation energy of product and deduce the mathematic model of accelerated degradation corresponding to the stress of natural random temperature.ResultsThe service life of a product in a typical region was given with the accelerated.The result of evaluation was in line with the expectation.ConclusionThe improved accelerated degradation model takes into consideration the impact of the random temperature in natural environment on the use of the product,thus it can better evaluate the service life of product.

service life;accelerated degradation factor;pseudo life distribution

10.7643/issn.1672-9242.2017.07.020

TJ760.6

A

1672-9242(2017)07-0097-06

2017-03-24；

2017-04-13

王彥霖（1974—），男，河南人，高級工程師，主要研究方向為可靠性工程及綜合保障技術。