基于最弱t-模的飛機起落架模糊故障樹分析

劉洪健，姚軍，李佩昌

（北京航空航天大學可靠性與系統工程學院，北京100191）

基于最弱t-模的飛機起落架模糊故障樹分析

劉洪健，姚軍，李佩昌

（北京航空航天大學可靠性與系統工程學院，北京100191）

目的針對飛機起落架部件失效的模糊性以及傳統模糊故障樹分析中采用擴展原理或區間運算而導致模糊積累的缺點，提出了一種基于最弱t-模的飛機起落架模糊故障樹分析新方法。方法采用梯形模糊數表示飛機起落架部件模糊失效概率，給出最弱t-模的模糊運算法則，并利用最弱t-模法則進行模糊故障樹分析。結果得到了飛機起落架系統的模糊失效概率以及部件的重要度。結論與傳統模糊故障樹分析方法比較，該方法具有更加靈活適用的優點，為飛機起落架可靠性評估奠定了基礎。

模糊故障樹分析；最弱t-模；飛機起落架；模糊數；可靠性評估

飛機起落架作為飛機的重要組成部分，對于飛機的安全起降發揮著至關重要的作用。據研究資料統計，由于起落架結構引起的事故占到飛機結構事故的2/3以上[1]。美國國家運輸安全委員會統計，1993—2003年10年內，各類飛機因起落架系統故障引起的飛行不正常事故占不正常飛行事故總數的15%，而其中因起落架收放系統故障引起的事故就占到了23%[2]。飛機起落架的安全性與可靠性受到廣泛關注，眾多研究者針對飛機起落架的故障分析開展了相關工作，并取得了一定的成果[3—5]。故障樹作為廣泛使用的系統可靠性分析方法，成功應用于飛機起落架可靠性分析中[6—8]。

在現實中，飛機起落架的故障現象、故障狀態以及故障原因等存在大量不確定性。不確定性主要包括隨機性和模糊性。基于隨機性的不確定性問題通常采用概率論理論進行分析，而模糊性主要是由于信息和認知的缺乏而造成的，包括數據的缺失或不足、故障定義的含糊不清以及環境的改變等[9—10]。為解決模糊性問題，Zadeh[11—12]在1965年開創性提出了模糊集合，采用模糊集定量化描述模糊問題，并于1968年提出了模糊算法。Tanaka等[13]首次將模糊集理論引入故障樹分析中，用梯形模糊數來表示基本事件的模糊失效概率，并利用擴展原理計算頂事件的失效概率區間值。在此基礎上，眾多研究者開展了模糊故障樹相關研究，文獻[14—17]采用不同模糊運算方法來分析系統模糊可靠性。Huang等[18]基于posbist可靠性理論，提出了一種posbist故障樹分析方法，該方法對于歷史數據缺失或失效概率很低情形下的可靠性評估具有優勢。隨著模糊算法的不斷發展，模糊故障樹分析方法也開始應用于飛機起落架模糊可靠性分析。李瑰賢等[19]采用模糊故障樹方法分析了直升機液壓系統可靠性，豐世林[20]針對民航運輸機剎車系統，采用模糊故障樹方法進行了模糊可靠性分析。

以上模糊故障樹分析方法都是基于最小邊界（sup-min）的評估方法，而這種可靠性評估方法會導致模糊累積。為緩解模糊的積累，Hong and Do[21]采用t-模邊界（sup-t-norm）代替最小邊界，提出了一種基于最弱t-模的模糊運算法則，并利用L-R型表示部件發生概率。近年來，基于最弱t-模的模糊運算方法受到廣泛關注，并成功應用于醫療器械[22]、印刷電路板[23]等眾多領域。

基于上述原因，文中采用梯形模糊數表示飛機起落架部件模糊失效概率，給出最弱t-模的模糊運算法則，并利用最弱t-模法則進行模糊故障樹分析，從而得到飛機起落架系統的模糊失效概率。與傳統模糊故障樹分析方法比較，該方法具有更加靈活適用的優點，為飛機起落架可靠性評估奠定了基礎。

1 飛機起落架模糊故障樹

1.1 最弱t-模模糊運算

實際工程中，許多系統的故障狀態、故障現象與故障原因之間存在著大量的不確定性，這種不確定性現象主要表現在隨機性和模糊性兩方面。對于隨機性問題，基于概率統計的方法被廣泛采用。對于模糊不確定性，一直以來困擾著廣大科研工作者，直到1965年，Zadeh[11]開創性提出模糊集合概念。

最常用的模糊數包括三角模糊數、梯形模糊數和高斯模糊數。早期的模糊運算方法主要是基于擴展原理或區間理論，而這些模糊算法會導致模糊累積現象，進而造成計算結果誤差較大。為解決這一問題，t-模被引入到模糊運算中。

t-模是單位區間[0,1]×[0,1]→[0,1]的二元函數T，函數T滿足交換律、結合律、單調性和邊界條件。

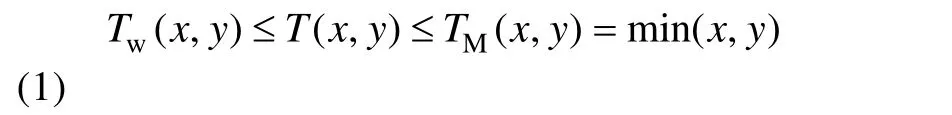
表1 基于Tw的模糊運算

對于兩個模糊數，基于TM和Tw的模糊加法和減法運算均可保持原有模糊數的形狀。對于模糊乘法運算，基于TM的模糊運算無法保持模糊數原有的形狀，而基于Tw的模糊運算則可以保持其形狀不變。另一方面，基于Tw的模糊運算方法可以緩解模糊擴展現象，有助于提高計算精度。

1.2 基于最弱t-模的模糊故障樹分析(FFTA)

故障樹分析作為一種重要的系統可靠性分析方法，主要依賴于基本事件的失效概率及其失效關系。實際工程中，由于數據的缺乏、環境變化等原因，難以獲得基本事件的失效概率精確值。為解決這類不確定性問題，采用模糊數來代替精確值的模糊故障樹分析被提出。模糊故障樹分析的關鍵在于基本事件間邏輯關系的模糊運算。

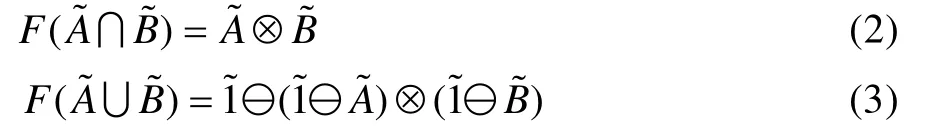
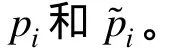
表2 不同方法下的邏輯門輸出失效概率

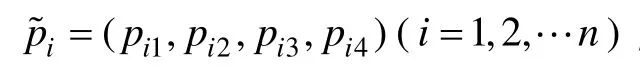
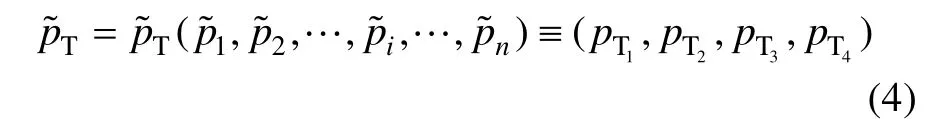
式中：(pT1,pT2,pT3,pT4)為梯形模糊數。

若假定底事件i的失效概率為0，則頂事件的模糊失效概率變為：

為定量評估底事件i對頂事件的影響程度，引入一種新的重要度定義：

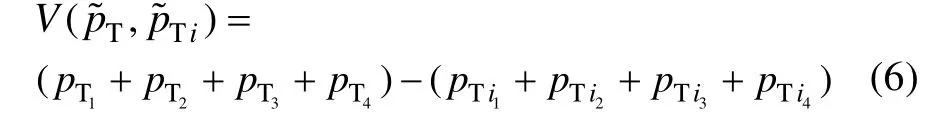
1.3 飛機起落架故障樹建立

起落架作為飛機的起降裝置，包括緩沖系統、收放系統、機輪剎車系統等，主要用于承受飛機自身重力和著陸時的沖擊載荷，吸收并消耗撞擊能量和飛機滑跑過程中顛簸產生的能量，保證飛機處于平穩狀態。因此，起落架的工作性能對于飛機起飛降落的安全性具有至關重要的作用。由于飛機起降周期較短，起落架的使用相對頻繁，而且起落架工作環境惡劣、受力復雜，導致飛機在壽命周期內發生故障的概率高于其他結構。

以某型艦載機為例，對飛機起落架的結構功能進行分析，并收集統計相關故障信息，參考文獻[8]，得到飛機起落架的主要失效模式。

對于緩沖系統而言，其主要故障包括減震支柱故障、扭力臂故障、斜撐桿故障以及輪胎故障。其中減震支柱的主要故障包括減震支柱出現滲油、減震支柱斷裂、活塞桿和外筒磨損、密封裝置受損；扭力臂的主要故障包括軸接頭磨損、螺栓磨損甚至斷裂；斜撐桿的主要故障包括螺桿的裂紋、襯套的磨損；輪胎的主要故障是輪胎的磨損。

對于收放系統而言，其包括主收放系統（液壓收放系統）和備用收放系統（機械收放系統）。液壓收放系統的主要故障包括收放鎖機構故障、收放作動筒故障以及液壓裝置故障。其中收放鎖機構的主要故障包括連接部位的磨損、鎖彈簧的斷裂；收放作動筒的主要故障包括收放作動筒滲油、活塞桿變形斷裂；液壓裝置的主要故障包括液壓泵故障、液壓管路泄漏。機械收放系統的主要故障是應急收放機構故障，包括應急開關無法開啟，應急作動筒斷裂以及上位鎖無法開啟等。

對于機輪剎車系統而言，其主要包括機輪故障和剎車組件故障，其中機輪故障主要包括機輪半軸磨損斷裂、軸承磨損以及輪胎磨損。

綜合以上飛機起落架故障分析，建立了飛機起落架的故障樹，如圖1所示。

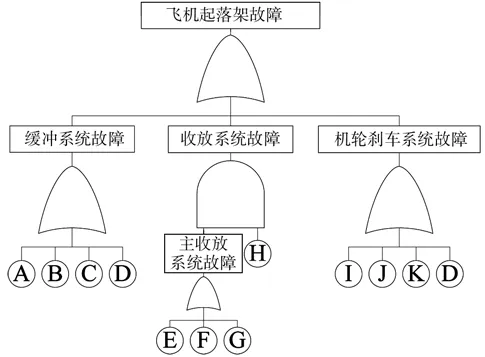
圖1 飛機起落架故障樹

根據文獻[7—8]提供的起落架失效概率或失效率信息，得到了故障樹中底事件在100 h工作時間下的失效概率。該失效概率由于飛機樣本問題、故障界限不夠明確、環境因素變化等問題，導致其數據存在一定的模糊不確定性。因此，根據其近似失效概率，通過梯形模糊數相關準則，仿真得到模糊失效概率，其數據見表3。

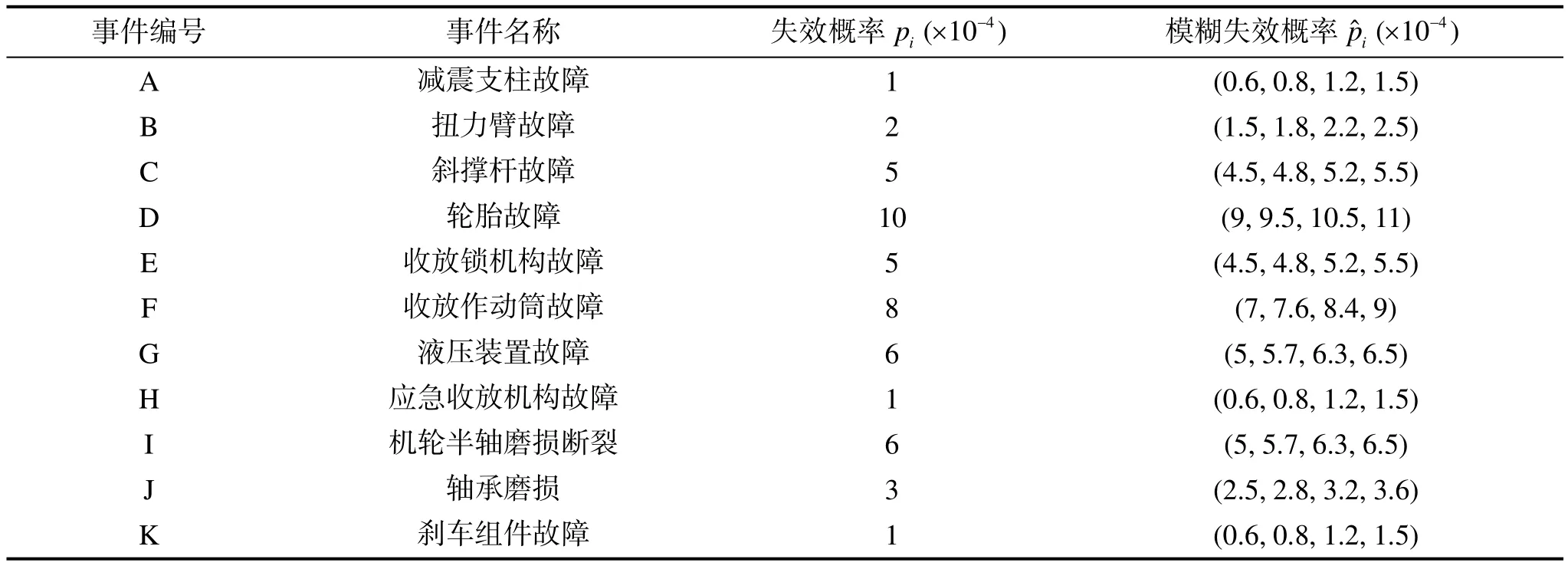
表3 底事件故障概率

2 飛機起落架的模糊可靠性評估

對圖1中故障樹進行分析，由布爾運算可得頂事件為：

采用不同的可靠性評估方法對飛機起落架的可靠性進行分析評估。

2.1 系統模糊可靠度計算

1）傳統故障樹分析方法。傳統故障樹分析依賴于基本事件失效概率精確值以及基本事件間的邏輯關系。由表2和式（7）可知飛機起落架的失效概率為：

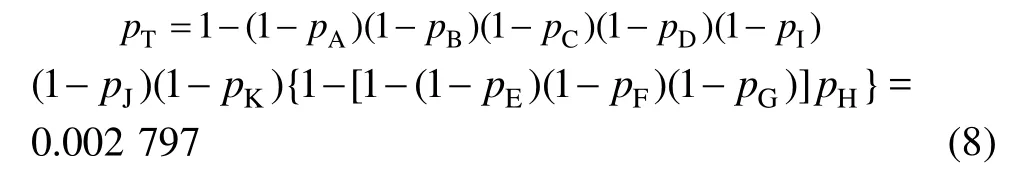
因此，飛機起落架在100 h工作時間下的可靠度為0.99720。

2）Huang方法。當歷史數據缺失或失效概率很低時，Huang提出的posbist故障樹分析方法對于系統可靠性評估具有較大優勢。由于飛機起落架失效概率很低，因此采用該方法對飛機起落架進行可靠性評估。

緩沖系統故障概率：

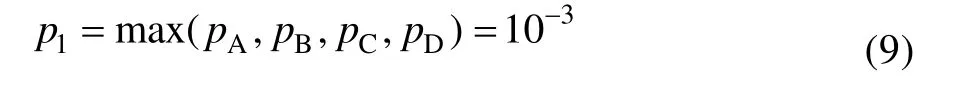
主收放系統故障概率：

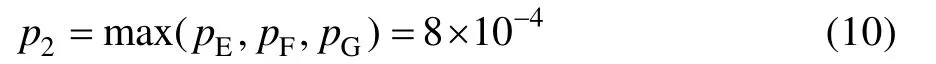
收放系統故障概率：

機輪剎車系統故障概率：

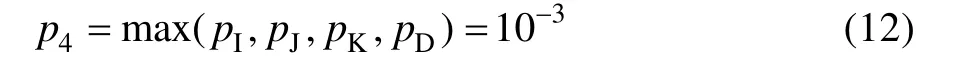
頂事件故障概率：

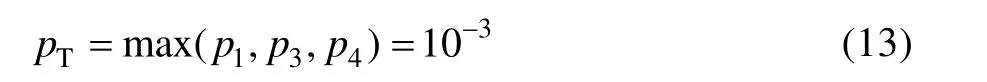
因此，在100 h工作時間下，飛機起落架失效概率為10-3，其可靠度為0.999。

3）Tanaka方法。Tanaka首次將模糊理論引入故障樹分析中，利用擴展理論進行模糊邏輯運算，進而得到頂事件的模糊發生概率。綜合表2和式（7），可得飛機起落架的模糊失效概率為：

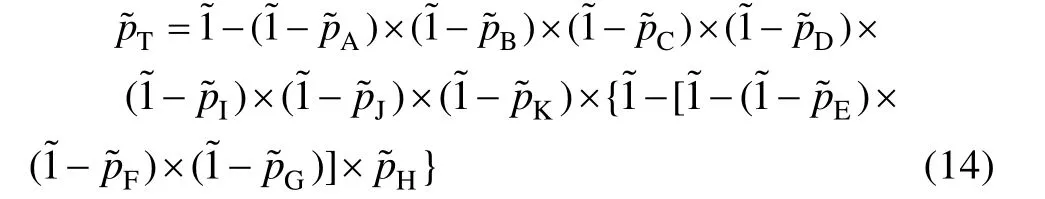
4）文中方法。文中將基于最弱t-模的模糊故障樹分析應用于飛機起落架系統，對飛機起落架進行可靠性評估。結合表2最弱t-模運算法則以及式（7），可知飛機起落架的模糊失效概率：

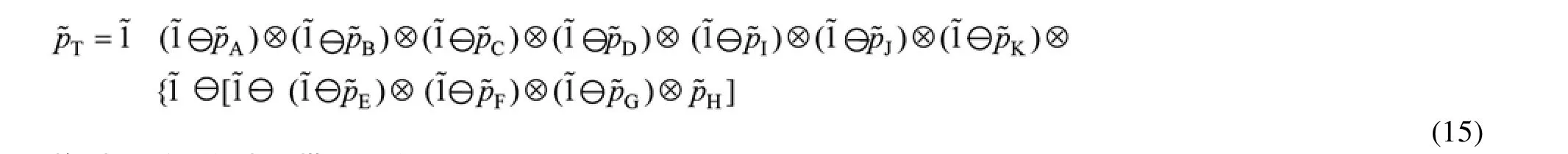
四種方法得到的飛機起落架模糊失效概率的隸屬度函數如圖2所示。

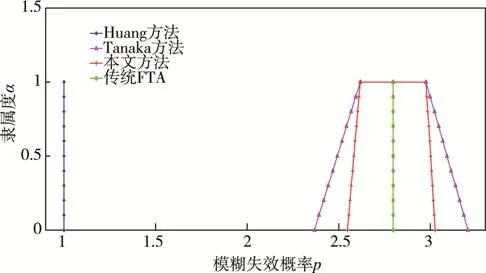
圖2 不同方法下的飛機起落架模糊失效概率

由圖2可知，文中方法能有效緩解模糊累積現象。考慮到隸屬度的置信水平α，不同置信水平下飛機起落架模糊失效概率見表4。

2.2 重要度分析

重要度分析是確定基本事件對頂事件影響顯著程度的有效方法。利用式（6）方法得到各基本事件的重要度見表5。

分析表5可知，輪胎和機輪半軸重要度最大，其對飛機起落架可靠性影響最顯著。因此，在飛機維修保養中，應重點關注輪胎的損傷以及機輪半軸的疲勞磨損，以保證飛機的安全起降。

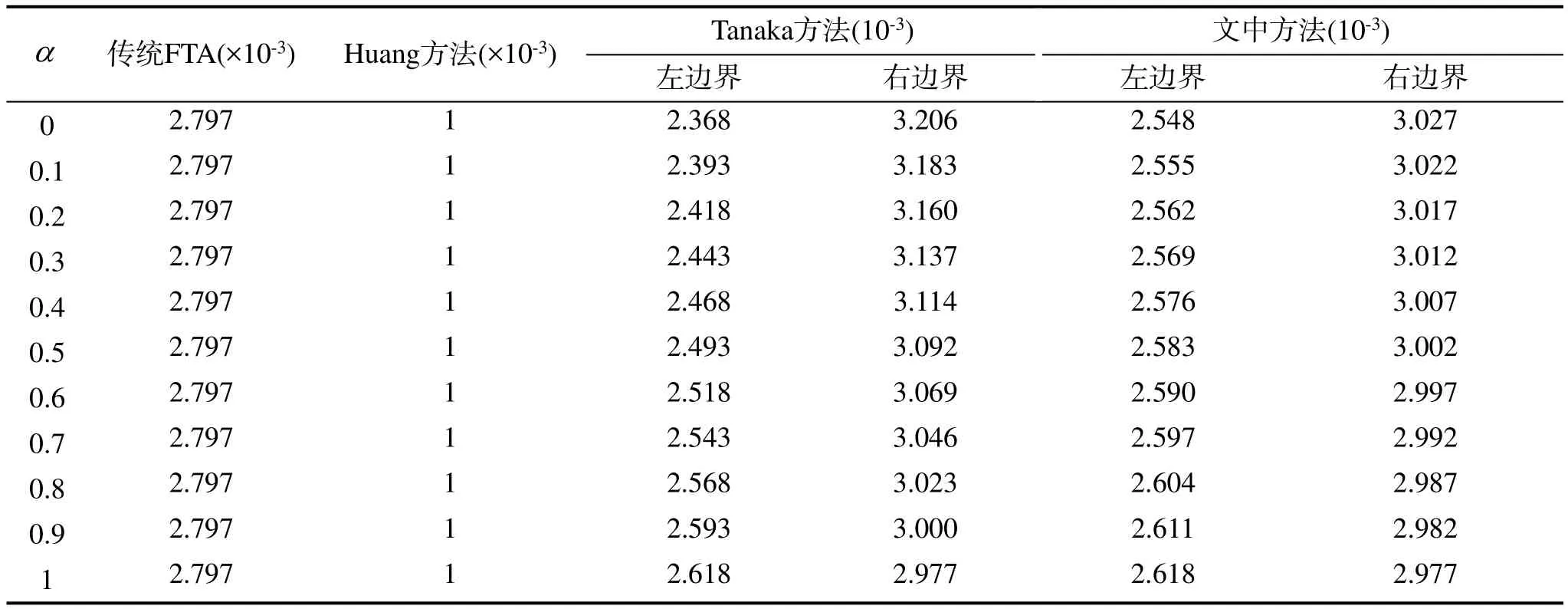
表4 不同方法下飛機起落架α-割集模糊失效概率

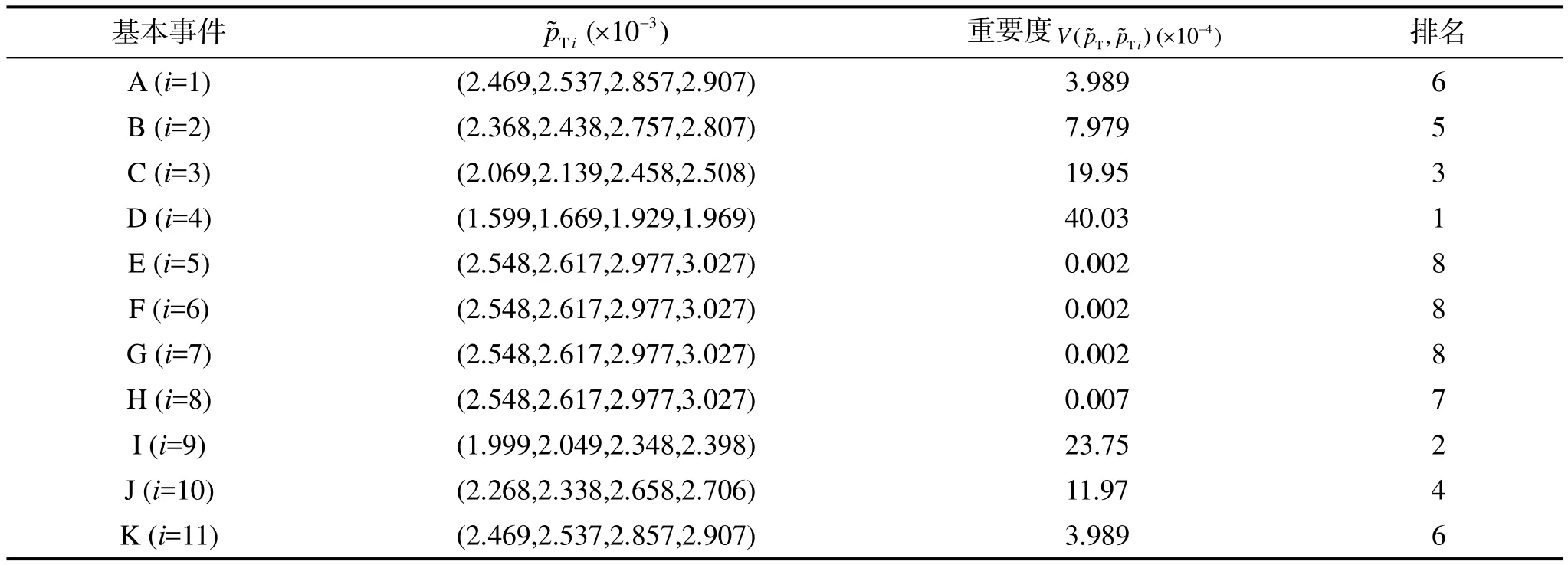
表5 基本事件重要度

3 結論

1）提出了基于最弱t-模的飛機起落架模糊故障樹分析方法，解決了飛機起落架故障數據存在不確定性時的可靠性評估問題。

2）與傳統模糊故障樹分析方法的對比結果顯示，文中方法能有效緩解模糊擴展理論和區間運算導致的模糊累積現象，說明了該方法在模糊分析中具有靈活適用的優點。

3）給出了不同置信水平下，飛機起落架系統的失效概率，并確定了飛機起落架部件的重要度，為飛機起落架的部件選用、結構改進以及確定防范措施的順序提供了依據。

參考文獻：

[1]NIE Hong.Fatigue Life Prediction of Aircraft Landing Gear Based on Multi-body System Simulation and Local Strain Method[C]//Fatigue 2000,Proceedings of the Fourth International Conference of the Engineering Integrity Society.Cambridge,England,2000:407—414.

[2]DUPOW H,BLOUNT G.A Review of Reliability Prediction[J].Aircraft Engineering and Aerospace Technology,1997,69(4):356—362.

[3]LEE H C,HWANG Y H,KIM T G.Failure Analysis of Nose Landing Gear Assembly[J].Engineering Failure Analysis,2003,10(10):77—84.

[4]OSSA E A.Failure Analysis of a Civil Aircraft Landing Gear[J].Engineering Failure Analysis,2006,13(7): 1177—1183.

[5]BAGNOLI F,DOLCE F,COLAVITA M,et al.Fatigue Fracture of a Main Landing Gear Swinging Lever in a Civil Aircraft[J].Engineering Failure Analysis,2008, 15(6):755—765.

[6]張峰,徐廷學,趙建忠,等.艦載直升機起落架收放系統事故樹的定性分析[J].航空科學技術,2009(5):18—20.

[7]張峰,路坤,徐廷學.事故樹的定量分析在某型艦載直升機起落架收放系統中的應用[J].飛機設計,2010, 30(1):64—68.

[8]李佩昌.某型飛機起落架的可靠性分析[D].哈爾濱:哈爾濱工程大學,2010.

[9]ZIO E.Reliability Engineering:Old Problems and New Challenges[J].Reliability Engineering and System Safety, 2009,94(2):125—141.

[10]SURESH P V,BABAR A K,RAJ V V.Uncertainty in Fault Tree Analysis:A Fuzzy Approach[J].Fuzzy Sets and Systems,1996,83(2):135—141.

[11]ZADEH L A.Fuzzy Sets[J].Information and Control, 1965,8(65):338—353.

[12]ZADEH L A.Probability Measures of Fuzzy Events[J]. Journal of Mathematical Analysis and Applications,1968, 23(2):421—427.

[13]TANAKA H,FAN L T,LAI F S,et al.Fault-Tree Analysis by Fuzzy Probability[J].IEEE Transactions on Reliability,1983,R-32(5):453—457.

[14]SINGER D.A Fuzzy Set Approach to Fault Tree and Reliability Analysis[J].Fuzzy Sets and System,1990, 34(2):145—155.

[15]MON D L,CHENG C H.Fuzzy System Reliability Analysis for Components with Different Membership Functions[J].Fuzzy Sets and Systems,1994,64(2): 145—157.

[16]CHEN S M.Fuzzy System Reliability Analysis Using Fuzzy Number Arithmetic Operations[J].Fuzzy Sets and Systems,1994,64(1):31—38.

[17]MON D L,CHENG C H.Fuzzy System Reliability Analysis for Components with Different Membership Functions[J].Fuzzy Sets and Systems,1994,64(2): 145—157.

[18]HUANG H Z,TONG X,ZUO M J.Posbist Fault Tree Analysis of Coherent Systems[J].Reliability Engineering and System Safety,2004,84(2):141—148.

[19]李瑰賢,于廣濱,馬良.基于模糊故障樹直升機起落架液壓系統的故障診斷方法研究[J].機床與液壓,2007, 35(5):214—216.

[20]豐世林.基于模糊故障樹的民航運輸機著陸防滯剎車系統故障診斷研究[J].液壓與氣動,2010(5):77—80.

[21]HONG D H,DO H Y.Fuzzy System Reliability by the Use of Tw the Weakest t-norm on Fuzzy Number Arithmetic Operations[J].Fuzzy Sets and Systems,1997, 90(3):307—316.

[22]KOMAL.Fuzzy Fault Tree Analysis for Patient Safety Risk Modeling in Healthcare under Uncertainty[J]. Applied Soft Computing,2015,37:942—951.

[23]KUMAR M.Applying Weakest t-norm Based Approximate Intuitionistic Fuzzy Arithmetic Operations on Different Types of Intuitionistic Fuzzy Numbers to Evaluate Reliability of PCBA Fault[J].Applied Soft Computing,2014,23(5):387—406.

[24]HONG D H.Fuzzy Measures for a Correlation Coefficient of Fuzzy Numbers under Tw(the Weakest tnorm)-based Fuzzy Arithmetic Operations[J].Information Sciences,2006,176(2):150—160.

Fuzzy Fault Tree Analysis of Aircraft Landing Gear Based on Weakest T-norm

L IU Hong-jian,YAO Jun,L I Pei-chang
(School of Reliability and System Engineering,Beihang University,Beijing 100191,China)

ObjectiveAccording to disadvantages of fuzziness on failure of landing gear components and application of extension principle and interval arithmetic in traditional fuzzy fault tree analysis leading to accumulation of fuzziness,this paper aims to propose a new analysis method for fuzzy fault of aircraft landing gear based on the weakest t-norm.MethodsThe fuzzy failure probability of aircraft landing gear components was represented by trapezoidal fuzzy number, and the fuzzy operation rules of the weakest t-mode were given,and the fuzzy fault tree analysis was carried out with the weakest T-norm rule.ResultsThe fuzzy failure probability of aircraft landing gear system and the importance of components were obtained.ConclusionCompared with the traditional fuzzy fault tree analysis method,the proposed method is more flexible and applicable,which lays a foundation for the reliability assessment of aircraft landing gear.

fuzzy fault tree analysis;weakest t-norm;aircraft landing gear;fuzzy number;reliability assessment

10.7643/issn.1672-9242.2017.07.021

TJ85；TG405

A

1672-9242(2017)07-0103-06

2017-03-18；

2017-04-06

劉洪健（1990—），男，河北人，碩士,主要研究方向為可靠性與環境試驗技術。

姚軍（1976—），男，北京人，高級工程師，主要研究方向為可靠性與環境試驗技術。