節點中心性對復雜網絡傳播模式的影響分析?
蘇臻 高超 李向華
(西南大學計算機與信息科學學院,重慶 400715)
節點中心性對復雜網絡傳播模式的影響分析?
蘇臻 高超?李向華
(西南大學計算機與信息科學學院,重慶 400715)
(2017年1月8日收到;2017年3月11日收到修改稿)
在眾多的重要節點評估方法研究中,具有較高中心性的節點一直是關注的焦點,許多傳播行為的研究也主要圍繞高中心性節點展開,因此在一定程度上忽略了低中心性節點對傳播行為的影響.本文從傳播異構性角度,通過初始感染最大中心性節點和最小中心性節點揭示網絡結構異構性對信息傳播的影響.實驗結果表明,傳播過程中存在“鏈型”和“扇型”兩種傳播模式,在初始感染比例不斷提升的情況下,兩種傳播模式的相互轉換引發傳播速率的變化,進一步促使非線性傳播規模交叉現象的產生.這一現象說明,在宏觀的信息傳播過程中,最小中心性節點的影響力不容忽視,尤其在初始感染比例升高時,最小中心性節點比最大中心性節點更具傳播優勢.
復雜網絡,結構異構性,中心性,傳播速率
1 引 言
復雜網絡中的重要節點挖掘作為網絡科學的重要研究內容之一,已經被應用到諸多領域,尤其在各類傳播行為(如流行病爆發[1]、信息擴散[2]、病毒傳播[3])的研究中體現得尤為重要.所謂重要節點是指相比于網絡中的其他節點,能夠對網絡的整體結構(如網絡連通性、平均距離等)以及功能(如網絡的魯棒性、同步等)產生重要影響力的一類特殊節點,其影響力主要體現在當這部分占比極少的節點受到影響時,會加速傳播過程,擴大傳播規模[4,5].由此可見,對于重要節點的挖掘非常重要.
目前,已有很多指標用于評估節點中心性(或者說影響力、重要性)[6,7],比如度數[8]、核數[9]、介數[10]以及特征向量中心性[11]等.盡管已有方法對傳播行為控制[12]、傳播源定位[13,14]以及傳播網絡推演[15]等起到了重要作用,但是這些研究都將研究的重點集中在具有較高中心性的節點上,在一定程度上忽視了具有較低中心性的節點對傳播行為的影響.因此,本著探究復雜網絡中傳播行為異構性的思路,首先發現了兩種不同的傳播模式(“鏈型”和“扇型”),然后通過實驗展現最大、最小中心性節點對傳播過程的影響.
本文基于四種常用的中心性評估指標(度數、核數、介數和特征向量),通過大量的傳播仿真實驗,揭示了傳播過程中的兩種傳播模式(“鏈型”和“扇型”)以及傳播規模交叉現象,即隨著初始感染比例的升高,初始感染最小中心性節點情況下的病毒傳播規模以及傳播速率會超越初始感染最大中心性節點的情況.與此同時,伴隨著初始感染比例的提升,兩種傳播過程下的傳播規模交叉時間點不斷提前.這一現象一方面說明節點中心性的高低對信息傳播起著重要作用,另一方面也反映復雜網絡中傳播行為的復雜性.
2 結構異構性
2.1 網絡結構異構性分析
從網絡的全局結構特征考慮,常見的規則網絡模型(如全局耦合網絡、最近鄰耦合網絡以及星形耦合網絡)在整體結構上表現出網絡平均距離小、鏈接度比較高的特點[16],但節點間的差異性不明顯,無法對實際網絡結構進行很好的刻畫.與規則網絡相反的隨機網絡,雖然與實際網絡存在相似的稀疏性、最大塊特性以及小世界特性,但在聚類特性以及度分布上仍然存在明顯的差異.考慮到規則網絡和隨機網絡分別在刻畫實際網絡小世界特征與聚類特性時的不足,小世界網絡模型作為過渡模型被提出[17].由于Erdos-Renyi隨機圖和Watts-Strogatz小世界模型中網絡的度分布可利用泊松分布來近似刻畫,因此這類網絡也被稱為均勻網絡或指數網絡[18].與此同時,Barabási和Albert[19]于1999年提出的Barabási-Albert(BA)無標度網絡模型作為揭示復雜網絡無標度特性的經典模型,使得無標度網絡成為當今網絡科學研究的重要課題之一[20].
從網絡傳播的角度考慮,對于均勻網絡,存在一個有限的正傳播臨界值表示網絡的平均度),當且僅當有效傳播率λ大于λc時,傳播行為才能得以保證并最終達到某一平衡狀態.在無標度網絡中,傳播臨界值對于冪指數為2<γ≤3的無標度網絡,當網絡規模無限增大時,該臨界值趨于0,即只要存在傳播源,傳播行為就會在整個網絡中蔓延[21,22].但這些分析有個假設,即利用平均場理論進行分析,使用平均度來度量網絡異構性.然而,鑒于節點位置差異導致網絡異構性(如中心性大小),尚需進行仿真分析.
2.2 節點結構異構性分析
從前面的分析可知,在規則網絡中節點間的差異性(如度差異性)不明顯,而在指數網絡以及無標度網絡中這種差異性表現突出,正是源于這種差異性造成了各節點中心性的差異.
本文從眾多評估方法中選擇四種常用指標(節點度、核數、介數和特征向量),討論結構異構性對傳播過程的影響.度中心性是刻畫節點重要性最簡單的指標,節點的度數越大則認為其影響力越高,因此度中心性主要是對節點的局部影響力進行刻畫[8,23].k-core分解與k-shell分解相似[9],都是對網絡節點重要性的一種粗粒化劃分,同樣地,k-core值越大則認為節點的影響力越高,利用k-core劃分在某些情況下能排除某些度中心性較高的節點從而找出具有更高影響力的節點.介數中心性刻畫了節點對于網絡中沿最短路徑傳輸的信息流的控制力[10],即經過某一節點的最短路徑越多則認為節點的重要性越高.介數中心性在控制網絡傳播[24]、對度中心性相同的節點進行更精確的劃分等方面能起到重要作用[25].特征向量中心性在考慮節點度的同時也考慮了鄰居節點的重要性[11],所以特征向量中心性能夠對節點的長期影響力進行很好的刻畫.
2.3 兩種傳播模式
基于已有的研究,從直觀的傳播效果來看,如果節點中心性越高,則認為其影響力越大,傳播能力越強,因此這類節點被作為傳播源的研究也相對廣泛.但是,在真實的傳播網絡中,并不是所有的傳播行為都是從高中心性節點開始,從低中心性節點開始的傳播行為在現實情況下也普遍存在.
本文通過前期實驗發現,在信息傳播過程中,由于網絡結構的影響,存在兩種可相互轉換的傳播模式:“扇型”和“鏈型”,如圖1所示.
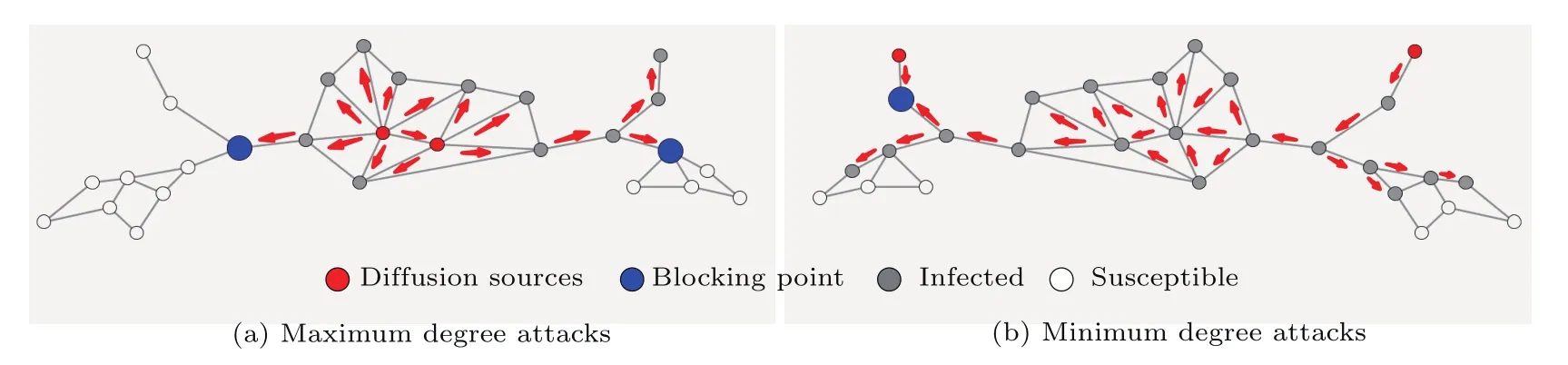
圖1 (網刊彩色)傳播過程中的兩種傳播模式 (a)“扇型”向“鏈型”轉變;(b)“鏈型”向“扇型”轉變Fig.1.(color online)Two kinds of propagation processes:(a)The change of di ff usion process from “fan-shaped”type to “single-strand”type if the highest-degree nodes are infected sources;(b)the change of di ff usion process from“single-strand” type to “fan-shaped” type if the lowest-degree nodes are infected sources.
當傳播過程從高中心性節點開始時,如圖1(a)所示,紅色傳播源均是高度數的節點,在短時間內,呈現出“扇型”的擴散方式,所以信息傳播的速率相對較快.但是,隨著傳播的繼續,一方面,越來越多的高鏈接度節點成為感染節點,無法為后續傳播過程提供持續快速的傳播速率;另一方面,傳播過程中存在“扇型”模式轉化為“鏈型”的情況,從而降低了傳播速率;再者,如果在鏈式結構中出現由于免疫等因素引起的傳播“中斷”,如圖1(a)中藍色的“中斷”點,后續節點則無法接收到傳播信息,從而進一步降低了傳播速率.
從低中心性節點初始的傳播過程則剛好相反,如圖1(b)所示,紅色傳播源均是度最小的節點,在傳播開始的短時間內,傳播模式主要呈現“鏈型”,所以傳播速率相對較慢.隨著傳播的繼續,一方面傳播模式會逐漸由“鏈型”轉化為“扇型”,從而提升傳播速率;另一方面,即使在“鏈型”傳播過程中出現“中斷”,只要任意一條傳播鏈得以繼續傳播,傳播速率都會得到增強,如圖1(b)中左側傳播路徑由于藍色“中斷”點的影響無法繼續,但是右側傳播路徑保證了傳播過程的繼續.由于兩種傳播模式的相互轉化,在不同初始感染條件下的傳播過程中,可能存在傳播規模交叉的現象,即兩種初始條件下的傳播過程在某時刻出現交叉點.
3 仿真分析
3.1 傳播模型
為了消除傳播模型對結果的影響從而驗證實驗結果的普適性,本文使用兩種不同信息傳播模型:交互式電子郵件模型[12]和傳統SI模型[26].
交互式電子郵件模型可以被看作是基于Agent的模型[12],在該模型中,傳播過程需要借助用戶的行為激發才能進行.具體來說,當網絡中的一個用戶被感染后,該用戶會試圖感染周圍用戶(即向郵件列表中的朋友發送郵件),而鄰居用戶只有在查看并點擊該用戶發送的郵件之后才會被感染.因此,傳播過程由兩種用戶行為決定:用戶查看郵件的時間和用戶是否點擊可疑郵件.定義N表示網絡中用戶的總數,i表示網絡中的用戶(i=1,2,3,···,N),Ti表示用戶i查看電子郵件的時間(即用戶i檢查電子郵件的時間間隔為Ti),Pi表示用戶i點擊可疑郵件的概率.通過分析可知用戶i查看電子郵件的時間Ti主要取決于用戶的個人習慣,而用戶i點擊可疑郵件的概率Pi主要取決于用戶對電子郵件病毒的了解程度以及系統自身的防護功能.由于網絡中用戶各自的行為相互獨立,所以該模型假設不同用戶間查看郵箱的時間間隔T與點擊可疑郵件概率P服從高斯分布,即對于某一具體用戶i,在不同時刻查看郵箱的頻率分布服從以Ti為參數的分布.依據文獻[12],本文用戶查看郵件的概率服從指數分布,其冪指數服從正態分布N(40,202),而用戶點擊可疑郵件的概率服從正態分布N(0.5,0.32).
SI模型,作為典型的傳染病模型之一[26],在研究許多傳播行為時都具有一定的適用性.在該模型中,只存在兩種狀態的個體,易染狀態(S:個體在被感染之前處于易染狀態,處于該狀態的個體可能被鄰居個體感染)和感染狀態(I:個體感染了病毒將處于感染狀態,并且處于該狀態的個體會嘗試感染其鄰居個體).在任意時刻,感染個體都會以概率β感染與之接觸的易染個體,直到傳播系統處于穩定狀態.在傳播網絡中表現為感染節點會以概率β嘗試感染與之直接鏈接的所有節點.為避免傳播速率過快的問題,本文設定易染節點被感染的概率β為0.2.
3.2 數據集
仿真實驗中采用的信息傳播網絡(G1—G12)均是具有無標度特性的網絡,在無標度網絡下的仿真結論能更好地付諸實際應用. 人工網絡(G1—G7)中,G1—G3、G4—G7分別是基于BA模型[19]和GLP(generalized linear preference)算法[27]生成的,其中G7包含多個社區結構.五個標準網絡(G8—G12)包含安然郵件網絡(G8)[28]、大學郵件網絡(G9)[29]、自治層Internet網絡(G10)[30]以及科學協作網絡(G11,G12)[31,32].所有網絡的結構特征信息如表1所列.
3.3 傳播實驗
本次傳播實驗基于不同中心性評估方法(度數、核數、介數、特征向量),重點分析了最大中心性節點以及最小中心性節點對傳播速率以及傳播規模的影響.其中,初始感染最大中心性節點的情景包括最大度、最大節點介數、最大核值以及最大特征向量中心性初始感染,而初始感染最小中心性節點的情景包括最小度、最小節點介數以及最小特征向量中心性初始感染.在不同的初始感染策略下,重復傳播100次,每次傳播過程的仿真迭代次數t為2000,保證最終傳播系統的穩定性的同時降低實驗結果數據的波動性,最后統計100次運行結果的均值作為實驗結果.
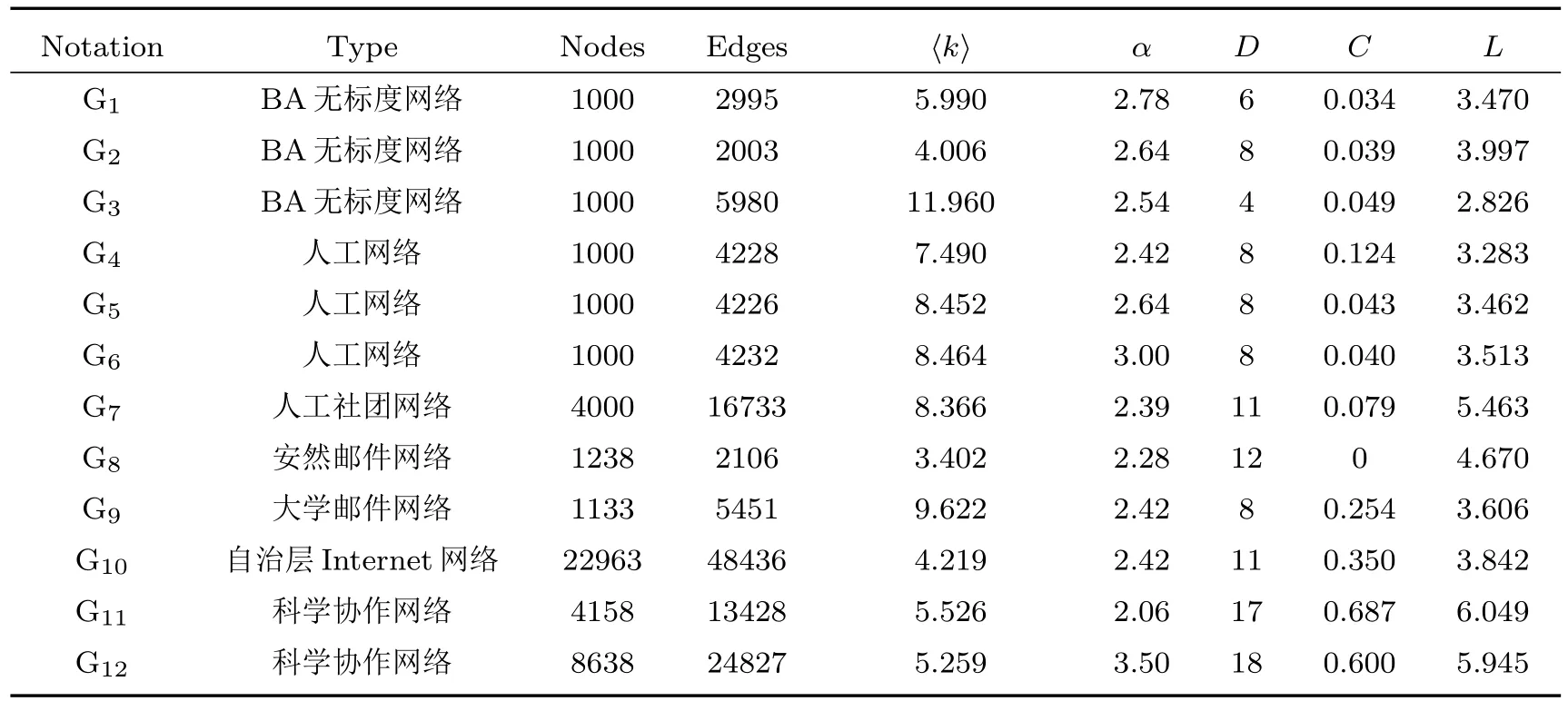
表1 網絡結構特征Table 1.Networks with di ff erent structures used in our experiments.
實驗結果包含兩部分:傳播交叉圖和交播交叉圖是對傳播規模與傳播速率交叉現象的直觀刻畫,包含傳播感染圖(即t時刻被感染節點總數I(t))和傳播增量圖(即t時刻新增感染數目?I(t)),I(t)和?I(t)滿足:?I(t)=I(t+1)?I(t).而交叉點非線性變化圖則進一步展現傳播規模交叉的時間點與初始感染比例間的變化關系.
3.3.1 傳播交叉現象
利用表1中的網絡數據,以電子郵件模型以及SI模型為傳播實驗平臺,在不同中心性評估方法下分別以5%,10%,20%的初始感染比例進行仿真實驗.以BA無標度網絡(G1)作為仿真結果示例,得到如圖2和圖3中的傳播交叉圖,其他數據集下的仿真證明見補充材料(online).
3.3.1.1 傳播感染圖
傳播感染圖是對傳播過程中傳播規模交叉的直觀呈現,在不同傳播初始比例下的四個傳播圖分別代表四種中心性評估方法下的傳播實驗,圖中的黑色標記點代表傳播規模發生交叉的時間點.圖2展現了不同傳播模型下BA無標度網絡(G1)中的仿真結果,其中圖2(a1)—(a3)來自電子郵件模型,圖2(b1)—(b3)來自SI模型,其他數據集下的仿真結果見補充材料的圖S1—圖S6(online).圖2中不同傳播模型下的仿真結果顯示出以下兩點現象:
1)本次實驗設計的初始感染比例下,在無標度網絡中,存在傳播規模交叉的現象,即初始感染最小中心性節點情況下的病毒傳播規模超越初始感染最大中心性節點的情況;
2)隨著初始感染比例的提升,交叉時間點呈現出不斷提前的趨勢,傳播規模交叉的現象也愈加明顯.
3.3.1.2 傳播增量圖
進一步分析傳播過程中傳播速率的變化,統計每次迭代過程中新增感染節點數目.傳播增量圖從傳播速率的角度對傳播過程進行刻畫.圖3與圖2中的傳播實驗一一對應,圖3(a1)—(a3)和圖3(b1)—(b3)分別展示了BA無標度網絡(G1)下基于電子郵件模型和SI模型的傳播增量圖,其他數據集下的傳播增量圖見補充材料的圖S7—圖S12(online).圖3中不同傳播模型下的傳播增量圖,顯示以下兩點特性.
1)在初始感染最大中心性節點的情況下,初期的傳播速率相對較快,但是初始感染比例的提升對這種傳播優勢有著明顯的抑制作用.相對地,在初始感染最小中心性節點的情況下傳播速率幾乎不受負面影響.
在電子郵件病毒傳播模型下,隨著初始感染比例的提升,初始感染最小中心性節點的情況下,傳播速率保持相對穩定.對比圖3(a1)—(a3)中的m1,m2和m3(即m1>m2>m3)可以發現,初始感染最大中心性節點情況下的傳播過程受到明顯的影響:達到最大傳播速率前的傳播加速率逐漸減緩;傳播過程中的最大傳播速率逐漸降低;相同傳播時刻下的傳播速率逐漸減小.
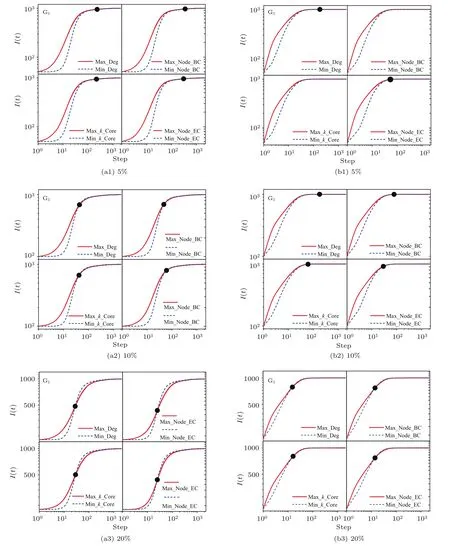
圖2 (網刊彩色)基于(a1)—(a3)郵件病毒傳播模型和(b1)—(b3)SI模型,初始感染比例為5%,10%和20%時病毒在BA無標度網絡(G1)中的傳播示意圖Fig.2.(color online)The illustration of dynamic propagation process in G1based on the(a1)–(a3)email propagation model and(b1)–(b3)SI model,in which 5%,10%and 20%nodes are selected as the initial infected nodes according to four di ff erent centralities(i.e.,degree,betweenness,k-core and eigenvector).
在SI模型中,通過對比圖3(b1)—(b3)中的n1,n2和n3(即n1>n2>n3)可以發現,隨著初始感染比例的提升,初期傳播加速率在數值上呈現出升高的趨勢,進一步引起相同傳播時刻下的傳播速率逐漸減小.而在初始感染最小中心性節點的情況下,前期的傳播速率呈現增強的趨勢.
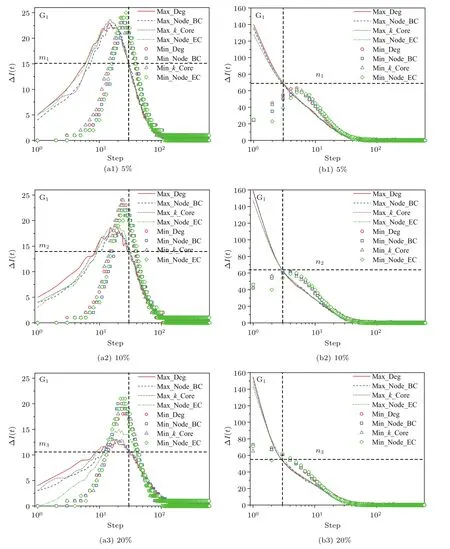
圖3 (網刊彩色)基于(a1)—(a3)郵件病毒傳播模型和(b1)—(b3)SI模型,初始感染比例為5%,10%和20%時病毒在BA無標度網絡(G1)中的傳播增量示意圖Fig.3.(color online)The illustration of dynamic changes of the incremental infected nodes in G1based on the(a1)—(a3)email propagation model and(b1)—(b3)SI model,in which 5%,10%and 20%nodes are selected as the initial infected nodes according to four di ff erent centralities(i.e.,degree,betweenness,k-core and eigenvector).
2)隨著初始感染比例的提升,初次傳播速率交叉點呈現出逐漸提前的趨勢.
結合圖2中的傳播感染圖,得到以下與傳播速率和傳播規模交叉相關的傳播特性:
1)在無標度網絡下,初始感染比例的不斷提高,會抑制初始感染最大中心性節點情況下的傳播速率,進一步影響傳播規模的擴散;相對地,初始感染最小中心性節點情況下的傳播速率幾乎不受負面影響;
2)兩種傳播過程受到的不同影響,促使其中的初次傳播速率交叉點呈現不斷提前的趨勢,進一步可能引起傳播規模交叉點的產生以及不斷提前;
3)不同結構下的無標度網絡中,傳播規模與傳播速率交叉點存在一定差異.
3.3.1.3 傳播模式分析
為了驗證傳播過程中存在的兩種傳播模式(即“扇型”傳播和“鏈型”傳播),以BA無標度網絡G1、人工網絡(G4)以及標準網絡(G9)為例,統計每次迭代過程中新增感染節點的平均度數?D(t).圖4給出了BA無標度網絡G1下的統計結果,其他數據集下的傳播模式驗證見補充材料的圖S13和圖S14(online).
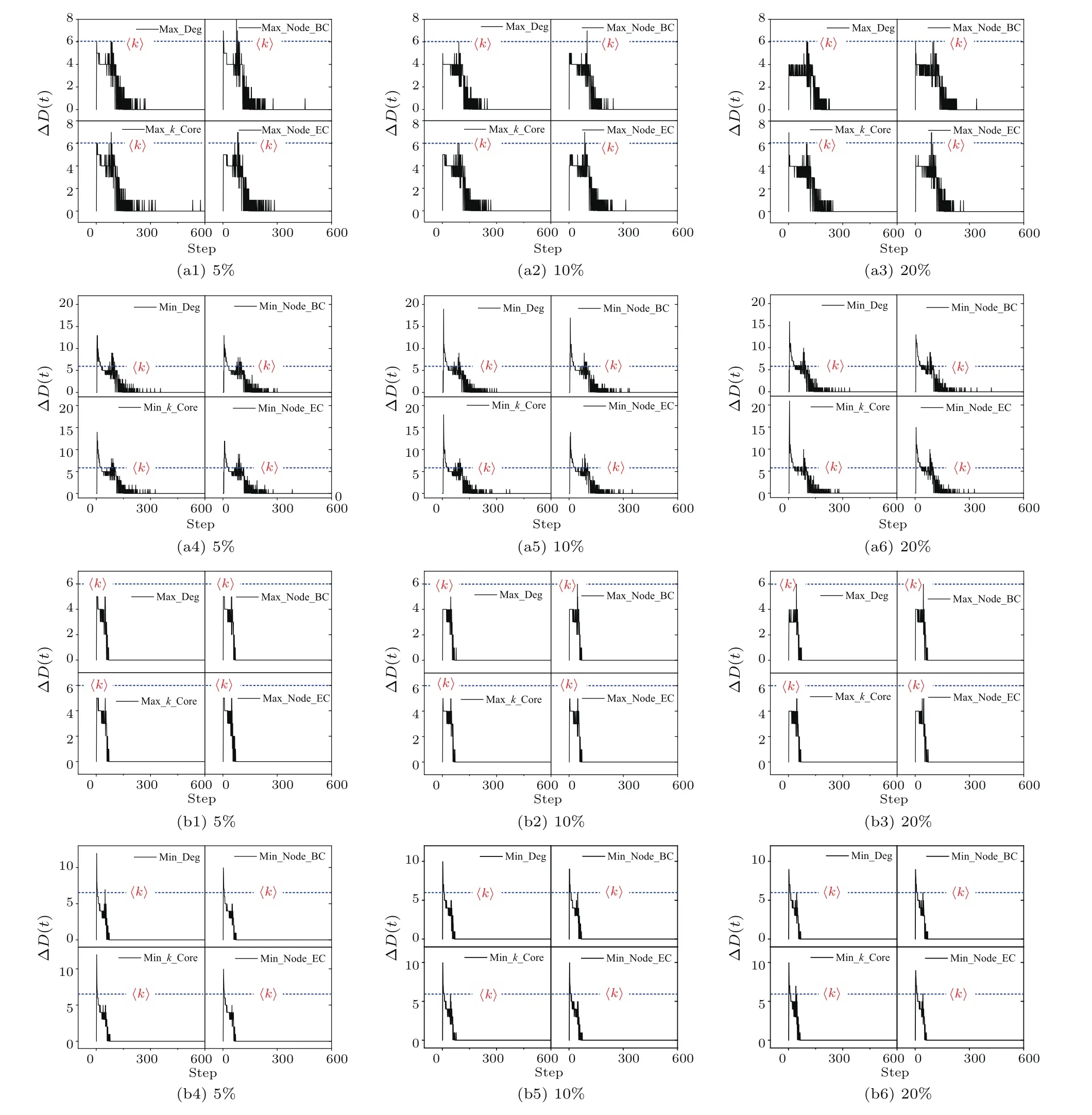
圖4 (網刊彩色)基于(a1)—(a6)郵件病毒傳播模型和(b1)—(b6)SI傳播模型,初始感染比例為5%,10%和20%時病毒在BA無標度網絡(G1)中的平均感染度示意圖Fig.4.(color online)The illustration of average degree of the incremental infected nodes in G1based on the(a1)–(a6)email propagation model and(b1)–(b6)SI model respectively,in which 5%,10%and 20%nodes are selected as the initial infected nodes according to four di ff erent centralities(i.e.,degree,betweenness,k-core and eigenvector).
圖4(a1)—(a6)和(b1)—(b6)分別來自電子郵件模型和SI模型,其中,圖4(a1)—(a3)和(b1)—(b3)、圖4(a4)—(a6)和(b4)—(b6)分別是初始感染最大、最小中心性節點情況下的統計結果,圖中〈k〉值表示網絡G1的平均度.圖4揭示出無標度網絡下,傳播過程中存在以下3點特性.
1)傳播過程中的平均感染度變化整體呈現下降趨勢直至傳播系統穩定,但是即使在初始感染最小中心性節點的情況下,傳播行為趨向于優先感染高鏈接度的節點.
2)基于郵件病毒的傳播過程中,平均感染度具有兩處明顯的峰值變化.在相同初始感染比例與中心性評價指標下,對比兩種傳播過程的平均感染度變化圖(如圖4(a1)和(a4),(a2)和(a5),(a3)和(a6))可以發現,隨著初始感染比例的升高,初始感染最小中心性節點的情況下,處于兩個峰值間的平均感染度明顯高于網絡平均度〈k〉,而初始感染最大中心性節點的情況下,整個傳播過程中的平均感染度明顯低于網絡平均度〈k〉.與此同時,對比圖4(a4)—(a6)可以發現,初始感染最小中心性節點下的峰值間的平均感染度呈現增強的趨勢.
在SI模型下,對比圖4(b1)和(b4),(b2)和(b5),(b3)和(b6)可以發現,初始感染最小中心性節點情況下的峰值依然高于初始感染最大中心性節點的情況.這一現象為傳播速率以及傳播規模交叉現象的產生提供了必要條件.
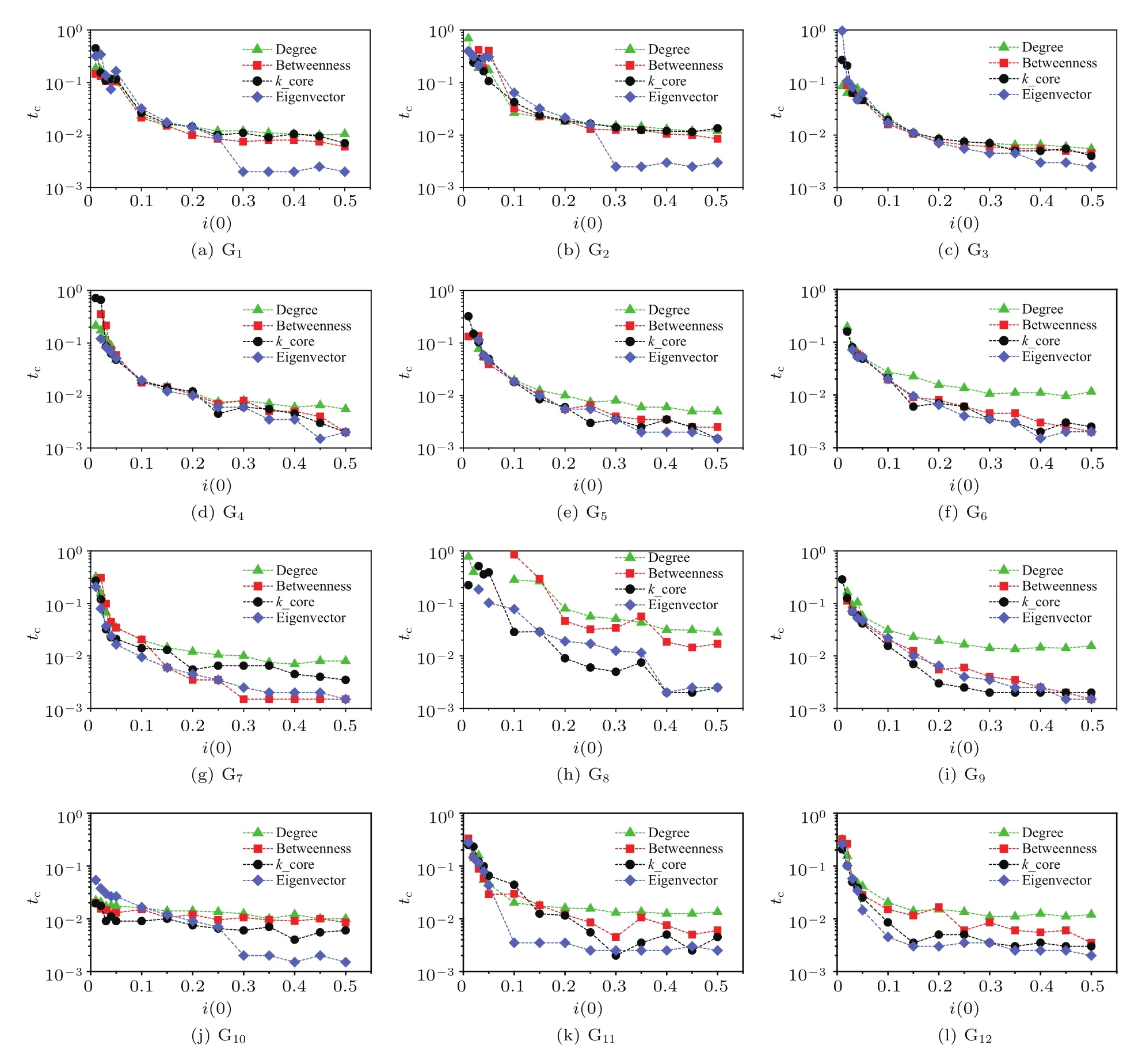
圖5 (網刊彩色)電子郵件病毒傳播模型下的交叉點非線性變化圖Fig.5.(color online)The relationship between tcand the i(0)based on the email propagation model.
3)基于郵件病毒的傳播過程中,兩處明顯的峰值現象以及傳播過程中的波動現象,說明傳播過程中的確存在兩種傳播模式.峰值間的傳播過程對應于傳播增量圖中?I(t)大于0的階段,在這一階段,平均感染度呈現不低的水平,說明傳播過程表現為“扇型”模式.當傳播增量圖中的?I(t)逐漸趨于0時,平均感染度從第二峰值處呈現降低趨勢,說明傳播過程表現為從“扇型”模式向“鏈型”模式的逐漸轉化.
3.3.2 初始感染比例對交叉點的影響
3.3.1小節中的仿真實驗揭示出,傳播規模以及傳播速率的交叉時間點會隨著初始感染比例的提升而提前.基于相同的傳播模型以及中心性評估方法,下面進一步探究交叉時間點與初始感染比例間的關系.
實驗中,初始感染比例i(0)從1%開始,分為兩段:1%—5%,按照1%的比例增長;5%—50%,按照5%的比例增長.不同初始感染比例下的交叉時間點tc與3.3.1小節中的交叉時間點對應,tc滿足:Imax(t) 不同的中心性評估方法、傳播模型以及網絡結構下,圖5和圖6的交叉點非線性變化圖揭示出以下3點共性: 1)初始感染比例較低時,存在傳播規模交叉的現象,但是,由于傳播過程具有一定的隨機性,當初始感染比例提升至10%—20%才能保證這一現象的穩定性; 2)交叉時間點隨著初始感染比例的提升逐漸提前,最后趨于穩定; 圖6 (網刊彩色)SI模型下的交叉點非線性變化圖Fig.6.(color online)The relationship between tcand the i(0)based on SI model. 3)傳播過程受到網絡結構的影響,進一步影響傳播規模交叉點的變化;在電子郵件病毒傳播模型下,G8網絡的交叉點表現出明顯的波動性,在SI模型下,初始感染比例提升至30%才產生傳播規模交叉的現象. 在第3部分的實驗中,利用不同的傳播模型以及無標度網絡證實了傳播過程中傳播速率與傳播規模交叉現象的存在.其中,3.3.1小節給出了這一現象的直觀驗證,3.3.2小節則通過進一步的實驗分析驗證了初始感染比例與傳播交叉現象間的關系.下面主要針對這一現象做進一步的分析. 基于微分方程的傳播模型存在均勻混合的假設,在一定程度上高估了傳播過程中的傳播速率[33].本文關注兩種極端情況下傳播過程中的傳播規模交叉現象,因此,采用離散化的方法對該現象進行分析. 定義如下:N,P(k)和〈k〉分別表示網絡中的節點總數,度為k的節點的比例和網絡的平均度;t時刻度為k的節點被感染的概率ik(t),t時刻感染節點的密度i(t);t時刻感染節點數I(t),t?1時刻到t時刻新增感染節點數?I(t),與第3部分中的統計量一致;平均傳播率,在SI模型下,該傳播率與節點被傳染的概率β一致,而在郵件病毒模型中,可將人類行為因素等效為異構化的傳播率,在分析過程中使用平均的傳播率.兩種傳播過程下,各變量分別采用上標進行區分. 仿真實驗中只考慮節點從健康轉變為感染狀態,根據文獻[33,34],傳播過程中t?1到t時刻: 其中,Θ(t)表示度為k的節點的感染鄰居的密度.進一步得到t時刻傳播速率與t時刻傳播規模的離散化表示: 根據(1)式可知,初始感染狀態i(0)對整個傳播過程影響重大.同時,(3)式表明,當傳播系統中感染節點比例較大的情況下,此時傳播規模交叉點的存在性取決于i(t),因此,需要對初始感染狀態i(0)以及i(t)進行分析. 初始狀態下滿足Imax(0)=Imin(0),由于無標度網絡的度分布可以用冪律分布(即P(k)~k?γ)近似刻畫,因此,在初始狀態下,存在感染密度的差異這必然會引起后續傳播行為的不一致性. 當系統中的感染節點比例足夠大(即感染節點中包含不同度值的節點),對(1)式從初始狀態ik(0)推導: 其中,fa(t)和fb(t)是關于t的多項式, (4)式第三步推導忽略了關于Θ(0)的高次項,第一項ik(0)描述初始狀態,第二項是對傳播增量密度的刻畫.傳播系統達到穩定狀態前,構建輔助函數Φ(t,Θ(0))=Imin(t)? Imax(t)且Imax(0)=Imin(0),則 當某時刻t出現傳播規模交叉的現象,根據Φ(t,Θ(0))>0進一步得到 隨著傳播行為的進行,存在 因此,為了避免傳播系統短時間內達到穩定狀態,當網絡規模趨于無限時,必然存在時刻tc使得(6)式成立.對于有限的網絡規模,通過提升初始感染密度i(0)同樣可以滿足(6)式,從而促使兩種傳播過程下傳播規模交叉現象的產生,并且隨著初始感染密度的提升,傳播規模交叉點的產生時間會得到提前.這一現象表明,初始感染最大中心性節點情況下,初始感染比例的提升會對傳播速率產生相對較強的負面影響. 結合第3部分的仿真實驗,無標度網絡下,由于網絡結構的影響,傳播過程中存在兩種傳播模式(“鏈型”和“扇型”),即使在初始感染最小中心性節點的情況下,傳播行為仍趨向于優先感染高鏈接度的節點,從而為傳播規模交叉點的產生創造了有利條件.再者,隨著初始感染比例的提升,初始感染最大中心性節點的情況下,高鏈接度的節點在初始狀態被感染,后續傳播速率受到相對抑制,進一步增大這一現象產生的可能性. 本文從網絡結構異構性的角度,基于不同的節點中心性,分析了結構異構性對傳播過程的影響.通過對傳播過程的分析,詳細闡述了傳播過程中存在的“鏈型”和“扇型”兩種傳播模式以及兩種傳播模式之間可能的轉換過程.以此為出發點,利用仿真實驗模擬病毒傳播過程,實驗結果表明,由于結構異構性的影響,傳播過程中的確存在兩種傳播模式(“鏈型”和“扇型”),并且在初始感染比例相對較高的情況下,這兩種傳播模式的相互轉換引起兩種極端傳播過程下的非線性傳播交叉現象.該現象揭示出初始感染比例的提高可以改變最小中心性節點的影響力,同時也提醒我們在今后的研究工作中有必要將這一因素納入考慮范圍. [1]Zhang H F,Zhang J,Zhou C S,Small M,Wang B H 2010 New J.Phys.12 023015 [2]Saito K,Kimura M,Ohara K,Motoda H 2016 Inform.Sci.329 985 [3]Fu C,Min L,Yang J,Xu D L,Liu X Y,Han L S 2015 Proceedings of IEEE International Conference on Computer and Information Technology;Ubiquitous Computing and Communications;Dependable,Autonomic and Secure Computing;Pervasive Intelligence and Computing Liverpool,United Kingdom,October 26–28,2015 p1725 [4]Ren X L,Lü L Y 2014 Chin.Sci.Bull.59 1175(in Chinese)[任曉龍,呂琳媛 2014科學通報 59 1175] [5]Zhao J,Yu L,Li J R,Zhou P 2015 Chin.Phys.B 24 058904 [6]Song B,Jiang G P,Song Y R,Xia L L 2015 Chin.Phys.B 24 100101 [7]Liu J G,Ren Z M,Guo Q,Wang B H 2013 Acta Phys.Sin.62 178901(in Chinese)[劉建國,任卓明,郭強,汪秉宏2013物理學報62 178901] [8]Freeman L C 1978 Soc.Networks 1 215 [9]Kitsak M,Gallos L K,Havlin S,Liljeros F,Muchnik L,Stanley H E,Makse H A 2010 Nat.Phys.6 888 [10]Liu Y Y,Slotine J J,Barabási A L 2011 Nature 473 167 [11]Borgatti S P 2005 Soc.Networks 27 55 [12]Gao C,Liu J M,Zhong N 2011 Knowl.Inf.Syst.27 253 [13]Jiang J J,Wen S,Yu S,Xiang Y,Zhou W L 2016 IEEE Trans.Depend.Secure.pp 1 [14]Zhang X Z,Zhang Y B,Lü T Y,Yin Y 2014 Physica A 442 100 [15]Han X,Shen Z S,Wang W X,Di Z R 2015 Phys.Rev.Lett.114 028701 [16]Wang X F,Chen G R 2003 IEEE Circ.Syst.Mag.3 6 [17]Strogatz S H 2001 Nature 410 268 [18]Watts D J,Strogatz S H 1998 Nature 393 440 [19]Barabási A L,Albert R 1999 Science 286 509 [20]Wang X F,Li X,Chen G R 2012 Network Science:An Introduction(Beijing: Higher Education Press)pp270–275(in Chinese)[汪小帆,李翔,陳關榮2012 網絡科學導論(北京:高等教育出版社)第270—275頁] [21]Pastor-Satorras R,Vespignani A 2001 Phys.Rev.Lett.86 3200 [22]Barthélemy M,Barrat A,Pastor-Satorras R,Vespignani A 2004 Phys.Rev.Lett.92 178701 [23]Albert R,Barabási A L 2002 Rev.Mod.Phys.74 47 [24]Goh K I,Kahng B,Kim D 2001 Phys.Rev.Lett.87 278701 [25]Estrada E,Rodríguez-Velázquez J A 2006 Physica A 364 581 [26]Pastor-Satorras R,Vespignani A 2001 Phys.Rev.E 63 066117 [27]Bu T,Towsley D 2002 Proceedings of the 21st Annual Joint Conference of the IEEE Computer and Communications Societies New York,USA,June 23–27,2002 p638 [28]UCBerkeleyEnronEmailAnalysisProject,MIT http://bailando.sims.berkeley.edu/enron/enron.sql.gz[2017-4-18] [29]http://deim.urv.cat/?aarenas/data/welcome.htm[2017-4-18] [30]University of Oregon Route Views Archive Project,David Meyer http://routeviews.org/[2017-4-18] [31]Stanford Network Analysis Project,Leskovec J https://snap.stanford.edu/data/ca-GrQc.html[2017-4-18] [32]Stanford Network Analysis Project, Leskovec J https://snap.stanford.edu/data/ca-HepTh.html[2017-4-18] [33]Zou C C,Towsley D,Gong W 2007 IEEE Trans.Depend.Secure.4 105 [34]Bogu?á M,Pastor-Satorras R,Vespignani A 2003 Statistical Mechanics of Complex Networks(Berlin:Springer-Verlag)p127 PACS:02.10.Ox,89.75.Fb,89.75.–kDOI:10.7498/aps.66.120201 Analysis of the effect of node centrality on diffusion mode in complex networks? Su Zhen Gao Chao?Li Xiang-Hua (College of Computer and Information Science,Southwest University,Chongqing 400715,China) 8 January 2017;revised manuscript 11 March 2017) The centrality re fl ects the importance of a node in a complex network,which plays an important role in the propagation dynamics.Many researches in the fi eld of node ranking estimation have revealed the characteristics of higher centrality in the structural dynamics and propagation dynamics.However,there are few reports about the e ff ect of nodes with a relatively lower centrality on propagation process.In this paper,we focus on the e ff ect of heterogeneous structural characteristics on propagation dynamics.First,we select four centrality measurements(i.e.,degree,coreness,betweenness,and eigenvector)and initialize source nodes with the maximum and minimum centralities respectively.Then,based on the email propagation model and the SI model,the massive numbers of elaborate simulations are implemented in twelve scale-free networks.These networks include three networks generated by the Barabási-Albert model,four synthetic networks compiled by the GLP(generalized linear preference)algorithm,and fi ve benchmark networks.The simulation results contain two parts:one is the crossover phenomenon of two propagation processes,and the other is the correlation between the crossover point and the proportion of the initial source nodes.We present the crossover of two propagations by calculating the total infected nodes,the incremental infected nodes,and the average degree of the incremental infected nodes.The average degrees of the incremental infected nodes in both synthetic networks and benchmark networks show that there exist two kinds of di ff usion modes(i.e.,“fan-shaped” type and “single-strand”type).With the increase of the initial source nodes,the interaction between two modes results in the di ff erent dynamic changes of two propagations with respect to propagation speed,which may lead to the crossover of two propagations in terms of propagation scale in the propagation process.Speci fi cally,the increase of the initial source nodes would suppress the propagation process in which nodes with the maximum centralities are portrayed as propagating sources.However,such an e ff ect is not observed in the propagation process in which nodes with the minimum centralities are portrayed as propagating sources.Our further simulation indicates that the crossover points appear earlier as the proportion of the initial source nodes increases.And by employing the discrete-time method,we fi nd that such a phenomenon can be triggered exactly by increasing the initial source nodes.This work reveals that the in fl uence of the nodes with the minimum centralities should be taken into consideration because the initial infected nodes with a lower centrality will lead to a larger propagation scale if the initial proportion is high. complex networks,heterogeneous structure,centrality measures,propagation speed 10.7498/aps.66.120201 ?國家自然科學基金(批準號:61402379,61403315)、 中央高校基本科研業務費專項資金(批準號:XDJK2016A008,XDJK2016B029)和重慶市科技研發基地建設計劃(國際科技合作)項目(批注號:cstc2015gjhz40002)資助的課題. ?通信作者.E-mail:cgao@swu.edu.cn ?2017中國物理學會Chinese Physical Society http://wulixb.iphy.ac.cn *Project supported by the National Natural Science Foundation of China(Grant Nos.61402379,61403315),the Fundamental Research Funds for the Central Universities of Ministry of Education of China(Grant Nos.XDJK2016A008,XDJK2016B029),and the Chongqing Science and Technology R&D Base Construction(International Science and Technology Cooperation)Project,China(Grant No.cstc2015gjhz40002). ?Corresponding author.E-mail:cgao@swu.edu.cn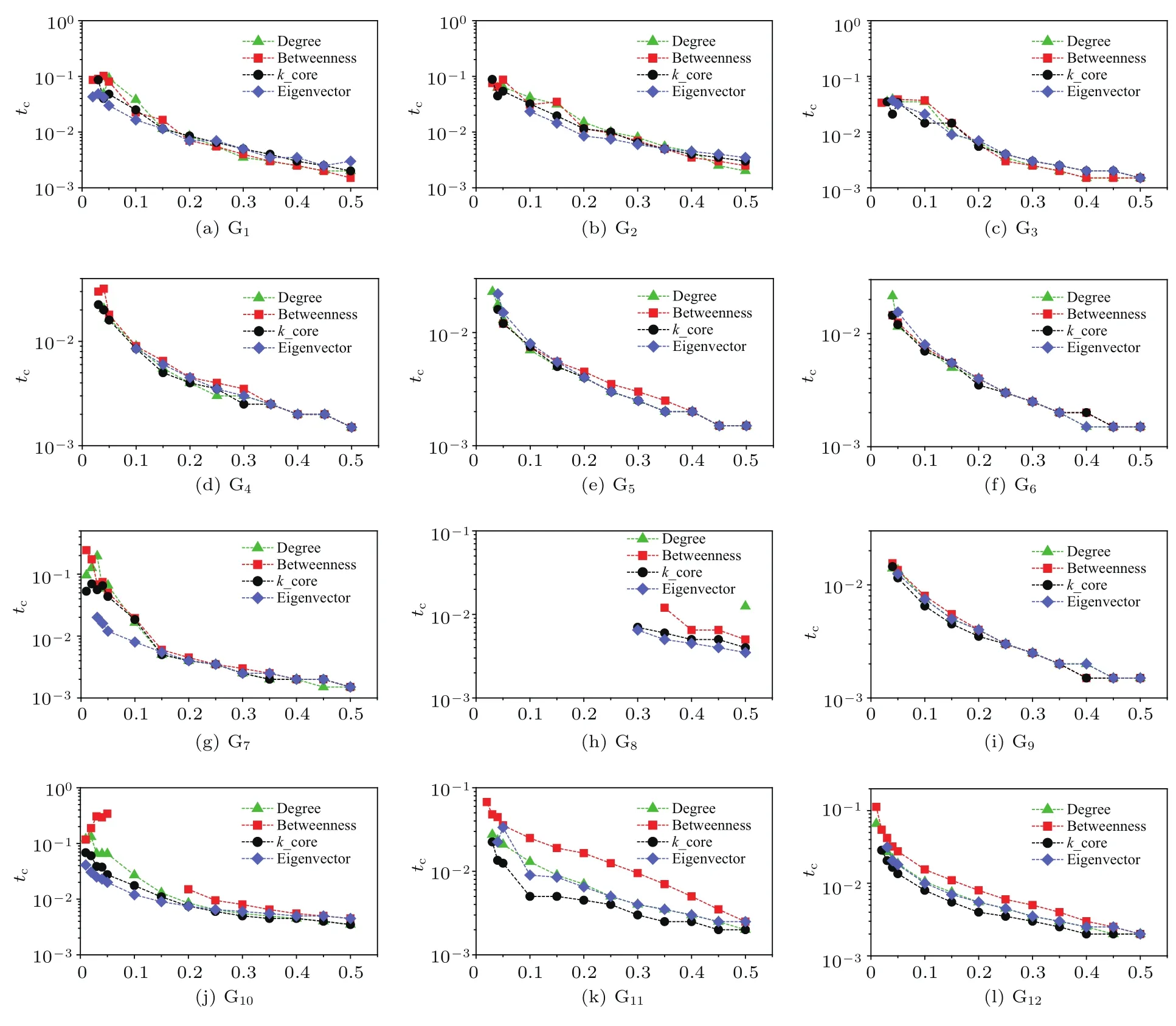
4 討 論
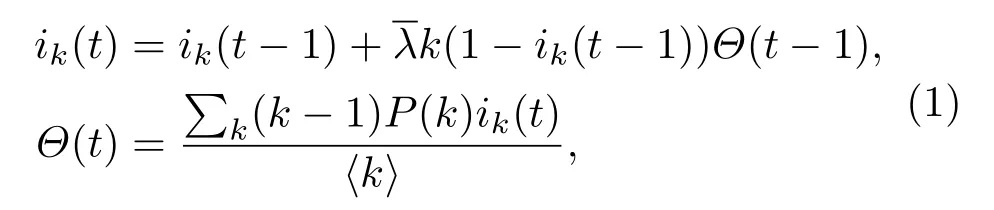
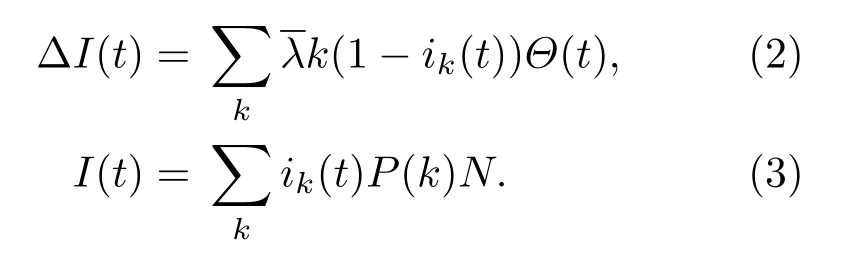
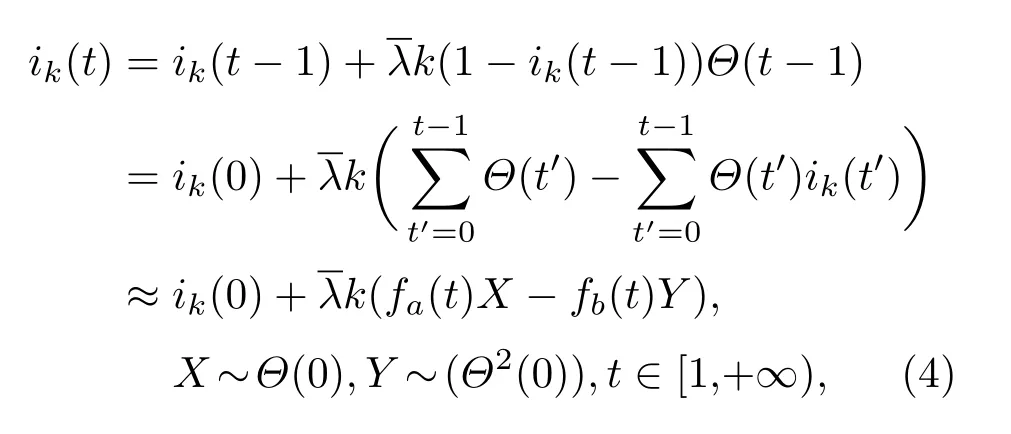
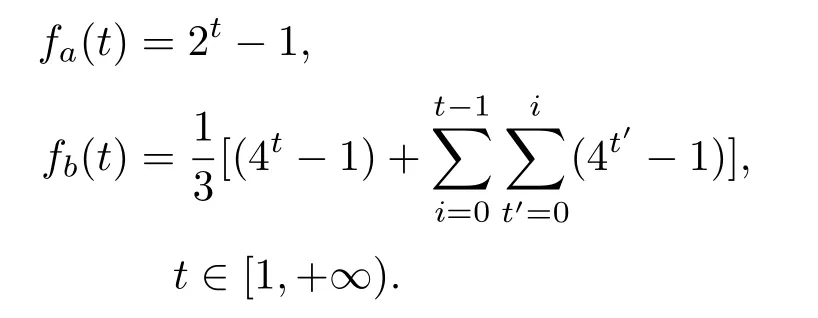
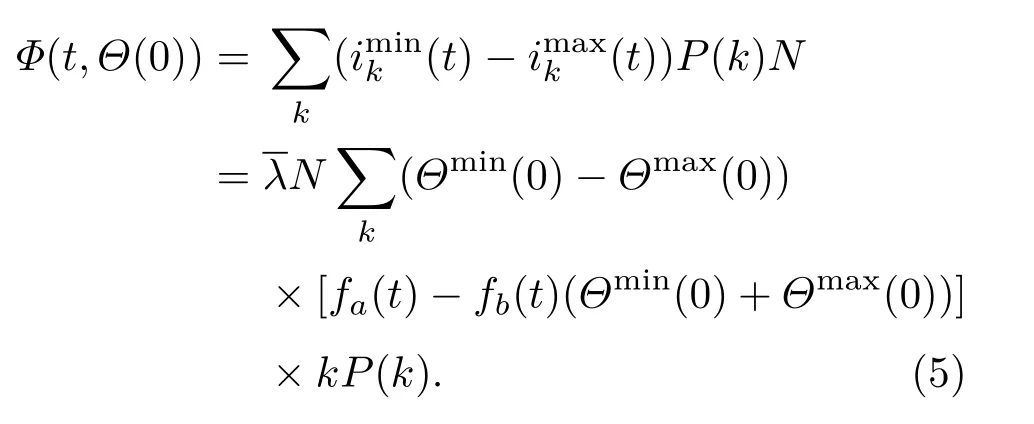
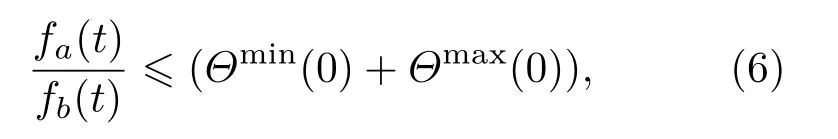
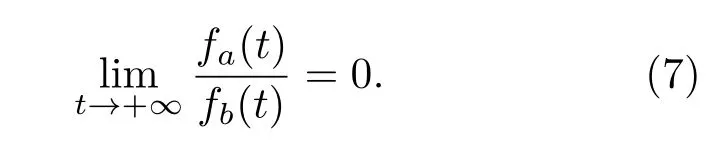
5 結 論

