雙列深溝球軸承剛柔耦合多體接觸建模與振動特性研究

蔣 玲 莉，卜 忠 頡，韓 清 凱,2，李 學 軍

(1.湖南科技大學 機械設備健康維護省重點實驗室， 湖南 湘潭 411201；2.大連理工大學 機械工程學院, 遼寧 大連 116024 )

雙列深溝球軸承剛柔耦合多體接觸建模與振動特性研究

蔣 玲 莉*1,2，卜 忠 頡1，韓 清 凱1,2，李 學 軍1

(1.湖南科技大學 機械設備健康維護省重點實驗室， 湖南 湘潭 411201；2.大連理工大學 機械工程學院, 遼寧 大連 116024 )

在研究雙列深溝球軸承各組件之間動力學關系的基礎上，基于彈性流體動力潤滑理論和赫茲接觸理論，利用多體動力學分析軟件ADAMS，結合有限元分析軟件ANSYS柔性化處理，建立了雙列深溝球軸承剛柔耦合多體接觸動力學仿真模型．綜合赫茲接觸剛度和潤滑接觸剛度的影響得到雙列深溝球軸承等效剛度．分析了不同荷載、轉速、油膜厚度對雙列深溝球軸承振動特性的影響，結果表明，合適的荷載可抑制雙列深溝球軸承振動；轉速的增加可加劇振動；隨著油膜厚度的增大，振動先減小后增大．研究結果為雙列深溝球軸承結構優化設計、減振降噪和運行狀態監測提供了參考依據．

雙列深溝球軸承；剛柔耦合；彈性流體動力潤滑；接觸剛度；振動特性

0 引 言

滾動軸承是機械設備的重要基礎零件，其振動特性直接影響整機的性能與使用壽命．機械設備高可靠性和高精度趨勢的發展，對軸承的振動特性提出了愈來愈高的要求，軸承的振動特性已成為機械行業研究的熱點內容之一．雙列深溝球軸承是機械行業中使用廣泛的一類滾動軸承，相較于單列深溝球軸承，其不僅可承受更高徑向負荷，還可以承受作用在兩個方向的軸向負荷，在航空航天、礦山、冶金和重型機械行業有著廣泛應用．開展雙列深溝球軸承振動特性研究，對雙列深溝球軸承結構優化設計、減振降噪和運行狀態監測均可提供參考依據，具有重要意義．

國內外已有部分學者開展了深溝球軸承的動力學建模與動態特性分析，文獻[1-3]對角接觸軸承的剛度進行了部分研究，分析了其動剛度特性；文獻[4]利用顯式動力學理論進行了滾動軸承動力學仿真分析；文獻[5-7]進行了滾動軸承的動態仿真和動態特性的分析；文獻[8]建立了滾動軸承的彈性接觸振動模型，探討了滾動軸承振動的本質．在以往大多數的研究中存在如下不足：忽略了油膜厚度對軸承接觸剛度的影響，將赫茲接觸剛度近似地看成軸承的剛度；忽略了軸承套圈的柔性體特征，無法真實反映滾動體和套圈之間的接觸力；以單列深溝球軸承為對象，對雙列深溝球軸承的振動特性研究較少．

基于此，本文以雙列深溝球軸承4205為研究對象，綜合赫茲接觸剛度和潤滑接觸剛度對軸承等效剛度的影響，將內外圈柔性化處理后，建立其剛柔耦合多體接觸動力學模型，研究雙列深溝球軸承在不同荷載、轉速及油膜厚度下的振動特性．

1 多體接觸模型及其等效剛度

雙列深溝球軸承結構簡圖如圖1所示，滾動軸承受載接觸時，滾動體與套圈之間將發生非線性彈性變形[9]．而滾動體與套圈之間的接觸荷載和接觸變形是研究其振動特性的關鍵因素．在ADAMS動力學仿真時，滾珠與內外圈接觸剛度的設置尤為重要，如果接觸剛度設置不合理，將直接影響接觸碰撞模型接觸力計算結果的準確性，從而影響軸承振動特性分析結果的正確性，導致仿真失敗．本文結合彈性流體動力潤滑理論和赫茲接觸理論，計算等效剛度，作為滾珠和內外圈之間的接觸剛度.

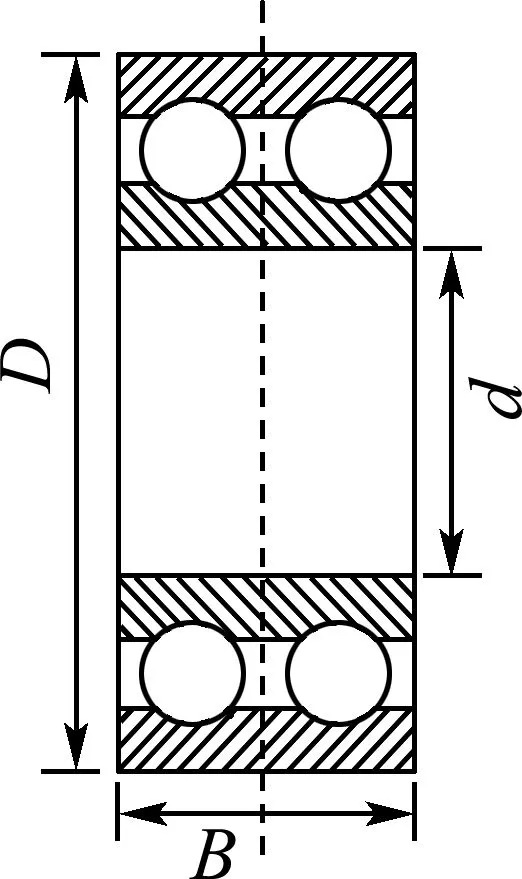
圖1 雙列深溝球軸承結構簡圖Fig.1 The structure diagram of double-row deep- groove ball bearing

1.1 赫茲接觸剛度

滾動軸承依靠滾道和滾動體的相互接觸來支承荷載[10]，赫茲接觸理論根據完全彈性的靜態接觸條件得出，滾動軸承的接觸問題符合赫茲接觸理論．根據赫茲接觸理論，滾動體與滾道接觸面是一個橢圓，如圖2所示.

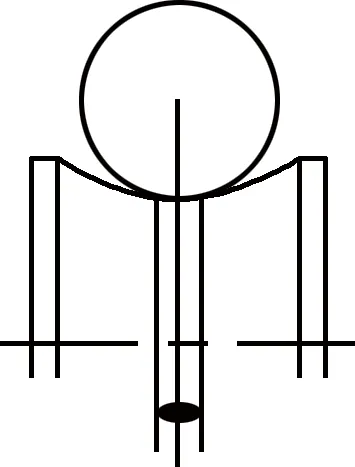
圖2 鋼球與滾道的接觸形態Fig.2 The contact form between steel ball and raceway

簡化解求得接觸面的形變量為

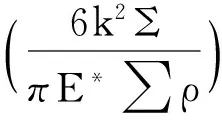
(1)

(2)

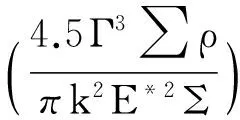
(3)

式中：a為橢圓接觸面的長半軸半徑；b為短半軸半徑；Q為接觸荷載；δ為最大彈性變化量；∑ρ為曲率和；Γ、Σ分別為第一類和第二類全橢圓積分；k為橢圓率；E*為等效彈性模量．

滾動軸承剛度是指軸承套圈在負荷方向上產生單位相對彈性位移量所需的外加負荷[11]，可表示為

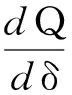
(4)

由式(3)變形得到滾動體與滾道接觸時所產生的接觸荷載為

(5)

式中：Ki(o)為滾動體與滾道接觸處的荷載變形系數[12]；δi(o)為滾動體與滾道的彈性變形；下標i、o分別表示內、外圈．

聯合式(4)、(5)得滾動體與滾道的赫茲接觸剛度為

(6)

1.2 潤滑接觸剛度

軸承在運轉過程中，滾動體和滾道接觸時會形成彈性流體潤滑油膜[13]．潤滑影響鋼球與滾道摩擦副的接觸特性，進而影響軸承的振動特性，彈性流體動力潤滑接觸模型如圖3所示.

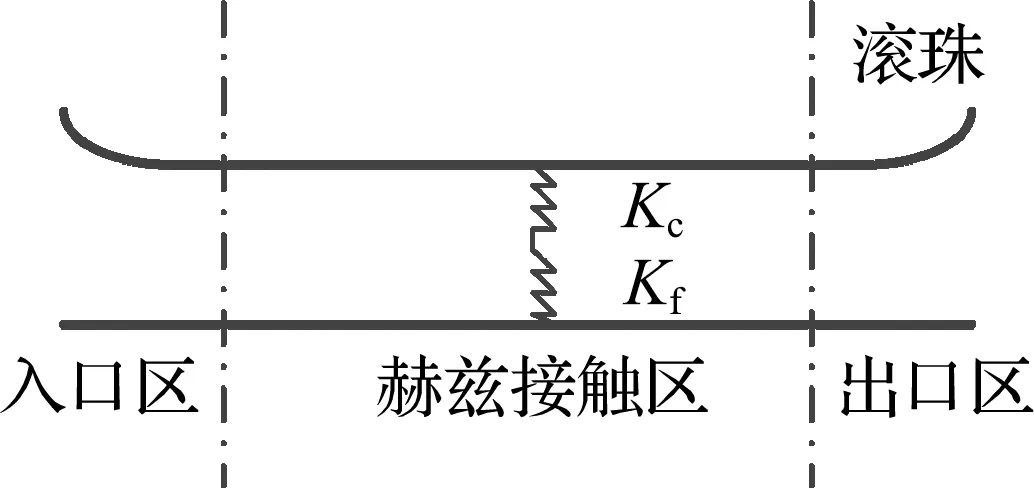
圖3 彈性流體動力潤滑接觸模型Fig.3 The contact model of elastohydrodynamic lubrication

根據彈性流體動力潤滑理論，最小油膜厚度決定了滾動軸承的油膜剛度．在等溫且充足供油條件下，滾動體與套圈之間量綱一最小油膜厚度為[14]

Hmin=3.63U0.68G0.49W-0.073(1-e-0.68k)

(7)

滾動體與套圈之間的油膜厚度為

hmin=HminRx

(8)

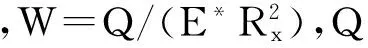
根據式(7)和(8)即可得到滾動體與套圈之間的油膜剛度為

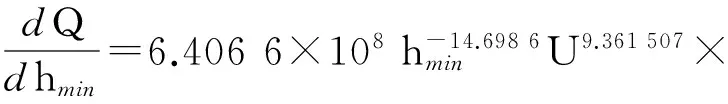
(9)

1.3 等效剛度

滾動軸承赫茲接觸剛度和油膜剛度串聯的鋼球-滾道等效剛度計算模型如圖4所示．通過式(6)和(9)得到的赫茲接觸剛度和油膜剛度，計算滾道和滾動體之間的等效剛度為

(10)

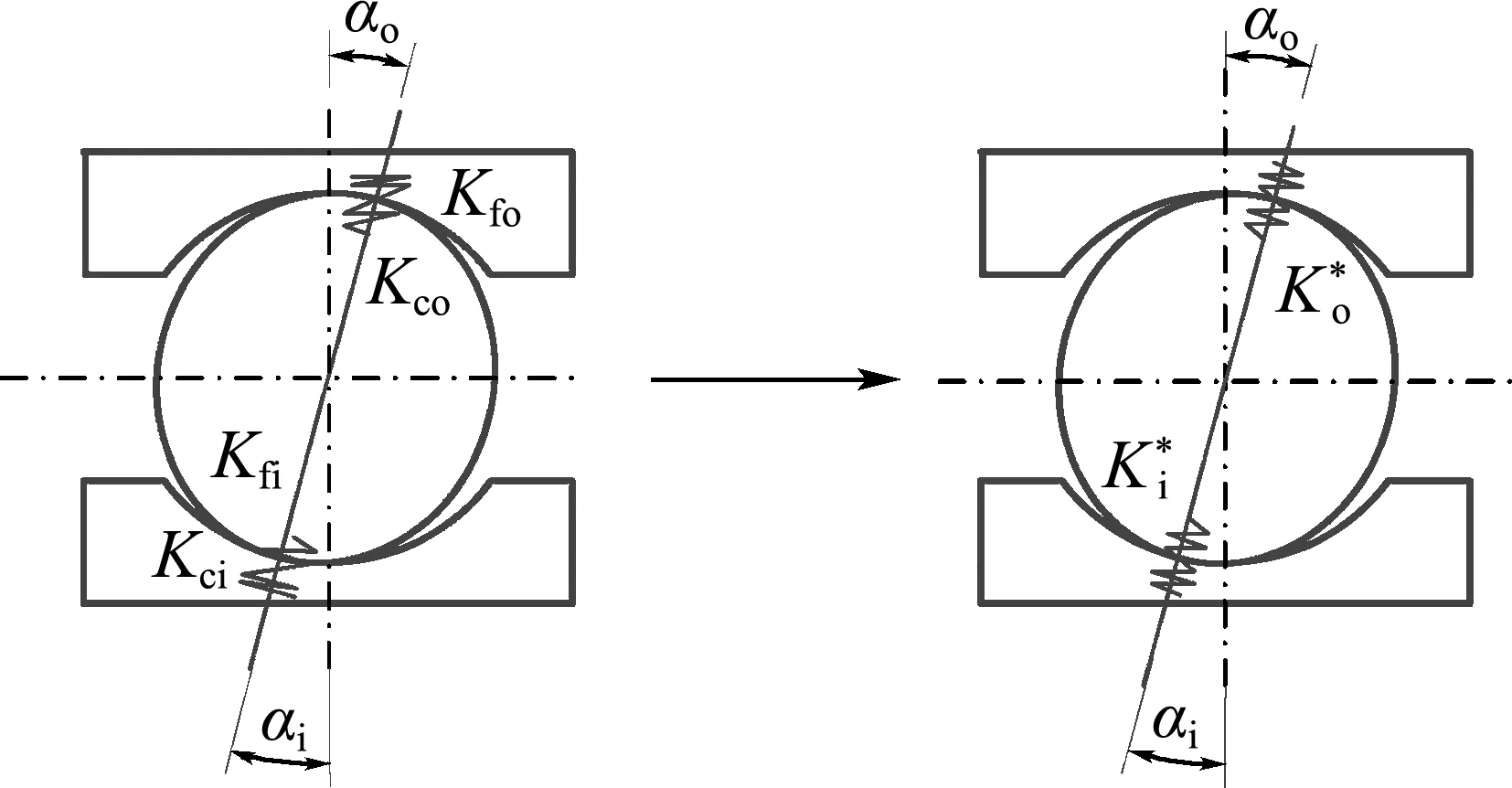
圖4 滾動體-滾道接觸副等效剛度計算模型Fig.4 The equivalent rigidity calculation model of contact pair between ball and raceway

2 剛柔耦合多體接觸動力學模型

本文以雙列深溝球軸承4205為研究對象，其基本結構參數見表1．計算所用到的潤滑油主要參數見表2．

表1 軸承結構參數Tab.1 The structure parameters of bearing

表2 潤滑油主要參數Tab.2 The main parameters of lubricating oil

運用CATIA軟件對雙列深溝球軸承進行三維建模，然后利用接口軟件SimDesigner導入ADAMS．ADAMS中默認的是全剛性體動力學分析，仿真分析時不考慮物體的小變形．如果把套圈當成理想的剛性體，則無法準確體現滾動體與套圈接觸微小區域的彈性接觸變形，從而無法真實有效地反映軸承的振動特性．而滾動體與套圈的彈性接觸面積是影響其接觸力和摩擦力的重要因素；元件之間的接觸力主要依靠套圈的形變傳遞[15]；把雙列深溝球軸承套圈設置為柔性體仿真時，能準確地還原其運動過程中滾動體和內外圈之間的相互作用力和彈性變形，進而準確地還原其振動特性．

本文利用有限元分析軟件ANSYS對雙列深溝球軸承的內外圈進行模態分析，生成模態中性文件，在ADAMS中替換剛性的內外圈．采用ADAMS中的Impact接觸力函數，定義了滾動體與套圈、保持架兜孔，保持架與套圈之間的接觸關系．其廣義形式表現為

(11)

其中采用了step函數，qo為兩物體的初始距離，q為兩物體實際距離，dq/dt為兩物體之間的距離隨時間的變化率；e為力指數，由赫茲接觸理論可取1.5；cmax為最大阻尼系數，s為切入深度，根據文獻[16]所述，可分別取10和0.1；K為接觸剛度，由赫茲接觸理論得出．

通過接觸的定義，利用虛擬樣機技術建立了基于內外圈柔性體的雙列深溝球軸承剛柔耦合多體接觸動力學模型，如圖5所示.

圖5 雙列深溝球軸承ADAMS仿真模型Fig.5 The ADAMS simulation model of double-row deep-groove ball bearing

3 雙列深溝球軸承振動特性分析

3.1 模型對比驗證

3.1.1 運動學特性分析 根據軸承各部件運動學關系，可以得到軸承零件之間的運動特性．由文獻[10]可知：當滾珠與滾道為純滾動時，可以推算出滾動體公轉線速度、滾動體自轉速度、保持架旋轉速度等運動學參數．在轉速為2 400 r/min時，仿真值與計算結果的對比如表3所示．

由表3可知，保持架旋轉速度、滾珠公轉線速度、滾球自轉速度的誤差分別為1.70%、1.97%、6.26%．所建模型的運動學仿真結果與理論計算誤差較小，模型滿足運動學特性．

3.1.2 頻譜特性分析 采用ADAMS進行多體動力學仿真，提取雙列深溝球軸承的振動加速度信號，進行頻譜特性分析．

表3 運動學參數仿真與計算值對比Tab.3 Simulation and calculation comparison of kinematic parameters

圖6～8為雙列深溝球軸承滾動體加速度的時域信號圖和頻域信號圖．其中x、z向為徑向，y向為軸向．由圖可知，徑向的時頻信號基本一致，且比軸向的振動大，主要特征頻率為16.23 Hz，與保持架旋轉頻率一致，軸向頻譜無明顯特征頻率，這與文獻[17]的分析結果一致．

剛柔耦合雙列深溝球軸承運動學仿真與頻譜特性分析驗證了模型的正確性．

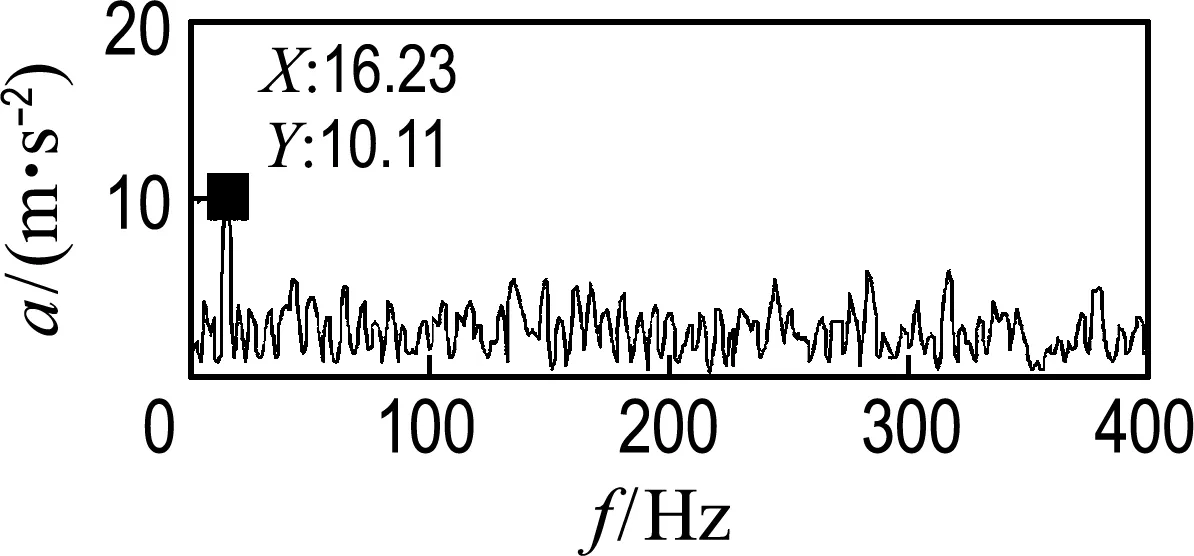
(a) 時域信號(b) 頻域信號

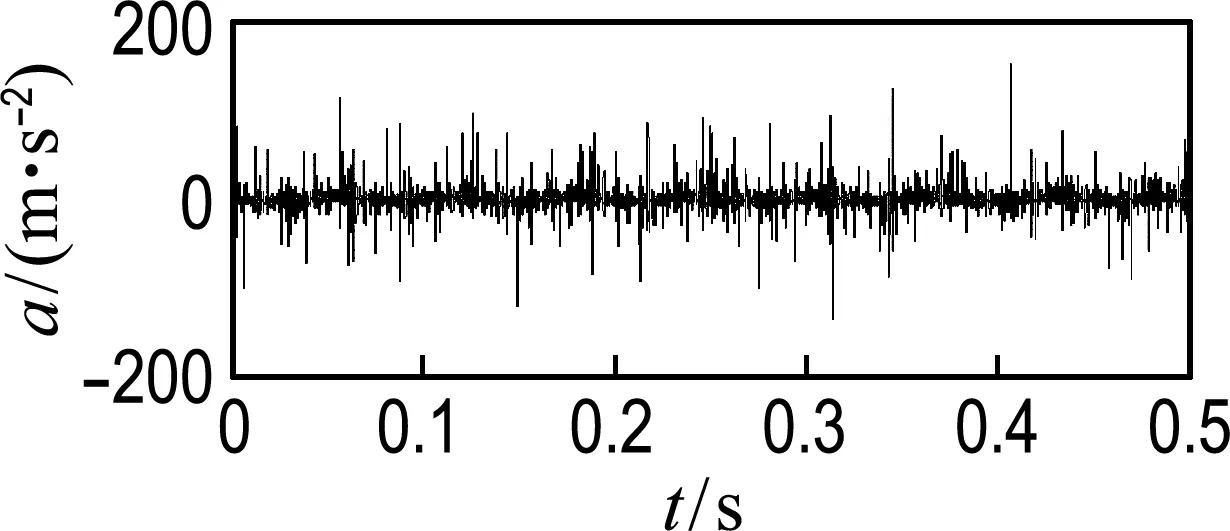
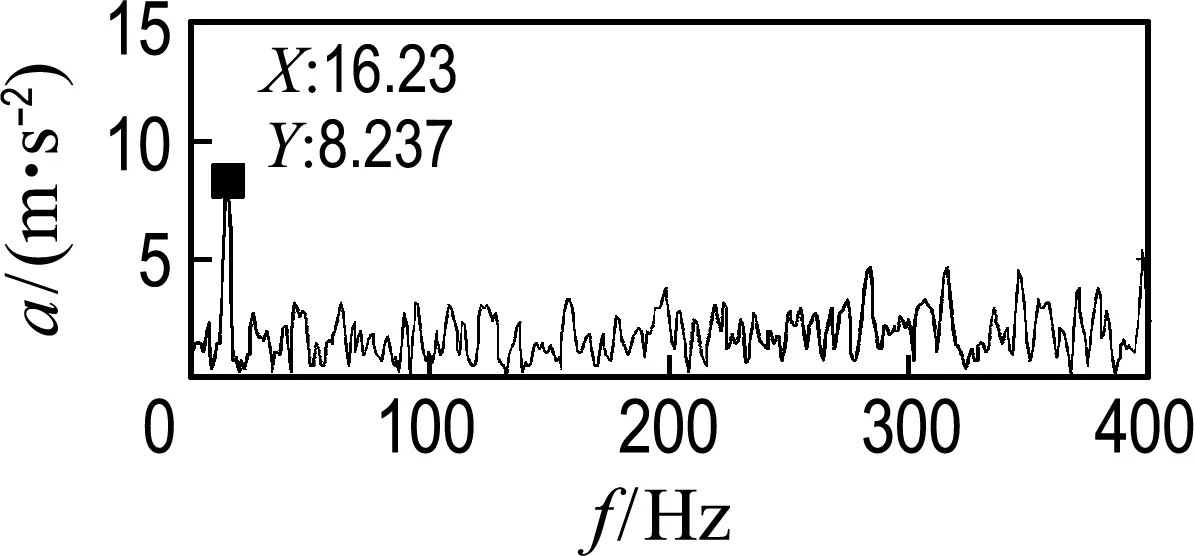
(a) 時域信號(b) 頻域信號

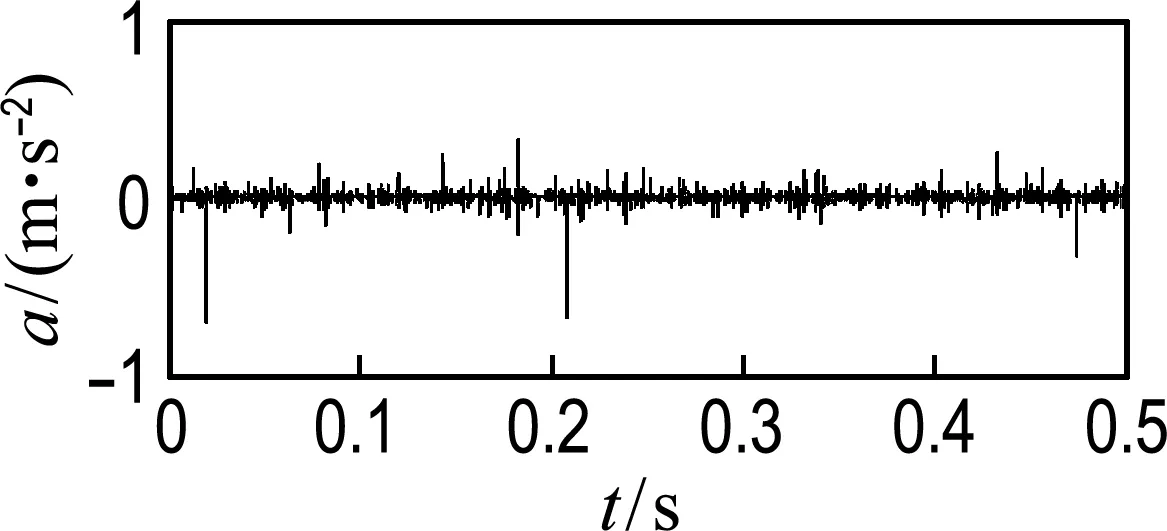
(a) 時域信號

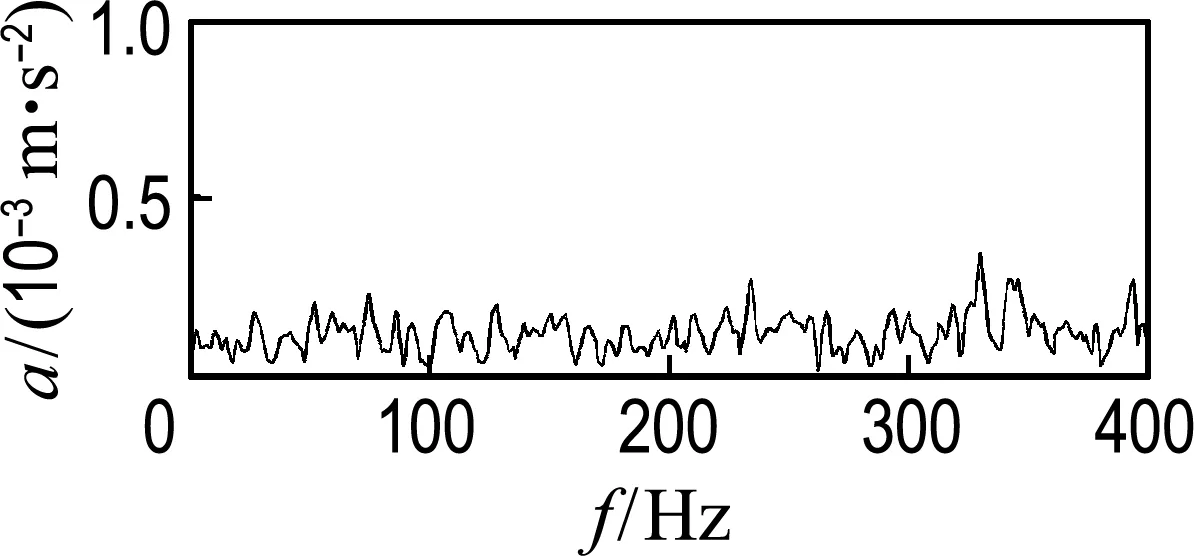
(b) 頻域信號

圖8 滾動體y方向加速度
Fig.8 Acceleration of rolling body iny-direction

3.2 荷載對軸承振動的影響分析

雙列深溝球軸承在承受的荷載發生變化時，會引起滾動體與套圈之間的接觸荷載改變，使得滾動軸承的接觸剛度產生相應的改變．而接觸剛度的改變使接觸副的接觸特性產生了變化，影響軸承的振動特性．根據上述等效剛度計算理論，得到不同荷載作用下的等效剛度，如圖9所示．由圖可知，隨著接觸荷載的增大，內外圈與滾珠之間的等效剛度增大；內圈與滾珠的等效剛度小于外圈與滾珠的等效剛度，且隨著接觸荷載的增大，二者的差值增大.

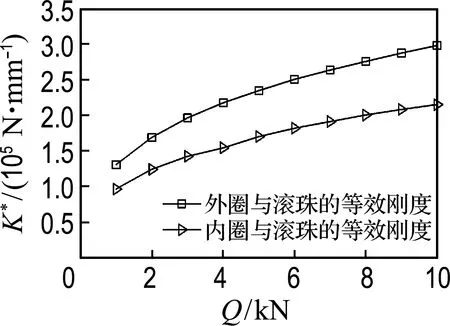
圖9 接觸荷載對等效剛度的影響Fig.9 The effect of contact load on equivalent stiffness

本文在ADAMS中對雙列深溝球軸承在不同荷載下的振動特性進行了仿真分析．

3.2.1 徑向荷載對軸承振動的影響 內圈轉速為600 r/min時，分別施以純徑向荷載以及聯合施加200、300、400 N軸向荷載，軸承振動與荷載的關系如圖10所示，圖中Fa表征聯合施加的軸向荷載值，縱坐標L表示軸承的振動加速度級．隨著徑向荷載的增大振動值增大，當徑向荷載較小時，聯合施加的軸向荷載增大將加劇振動；隨著徑向荷載的增大，聯合施加的軸向荷載反而可在一定程度上抑制振動．本文分析案例中當徑向荷載大于1 000 N時，聯合施加的軸向荷載對振動有一定的抑制作用.

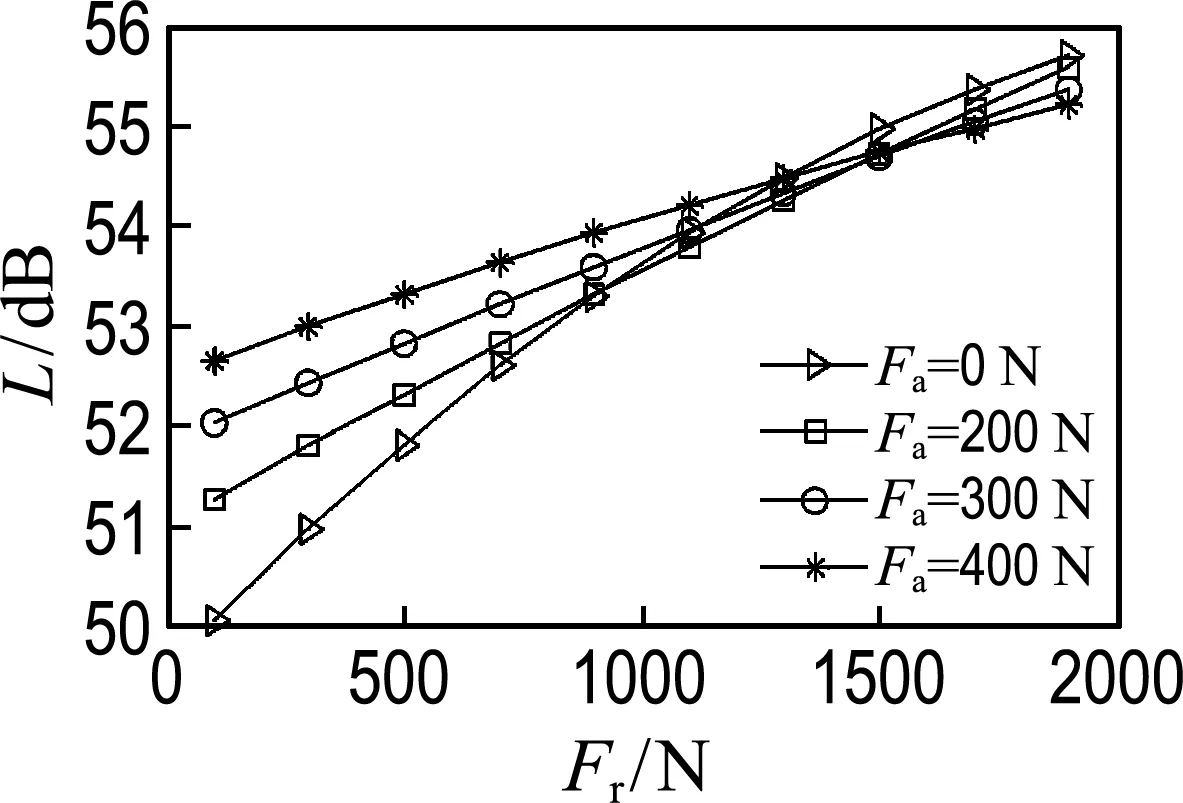
圖10 徑向荷載與軸承振動的關系Fig.10 The relationship between radial load andnbearing vibration

3.2.2 軸向荷載對軸承振動的影響 內圈轉速為600 r/min時，分別施以純軸向荷載以及聯合施加300、500、1 000 N徑向荷載，軸承振動與荷載的關系如圖11所示，圖中Fr表征聯合施加的徑向荷載值，橫坐標μ表示軸向荷載與額定動荷載的比值，縱坐標L表示軸承的振動加速度級．當軸向荷載較小時，聯合施加的徑向荷載增大將加劇振動；隨著軸向荷載的增大，聯合施加的徑向荷載反而可在一定程度上抑制振動．說明合適的軸向與徑向荷載共同作用對雙列深溝球軸承的振動均有抑制作用.

圖11 軸向荷載與軸承振動的關系Fig.11 The relationship between axial load andnbearing vibration

3.3 轉速對軸承振動的影響分析

軸承的轉速影響滾動體與內外圈接觸副中潤滑油膜的形成，導致油膜剛度產生變化．隨著轉速的增大，滾珠與套圈之間的油膜剛度減小，等效剛度的變化主要來源于油膜剛度的變化，這是由轉速增大，滾珠和套圈之間的潤滑油流速增大造成的．根據上述等效剛度計算理論，可以得到轉速對等效剛度的影響，如圖12所示.

圖12 轉速對等效剛度的影響Fig.12 The effect of rotational speed on equivalentnstiffness

徑向荷載和軸向荷載同時為500 N時，內圈轉速與軸承振動關系如圖13所示，縱坐標L表示軸承的振動加速度級．隨著內圈轉速的增大，軸承振動呈近似線性增大.

3.4 油膜厚度對軸承振動的影響分析

油膜的形成對雙列深溝球軸承振動特性的影響很大，合理控制油膜的厚度是抑制軸承振動的關鍵．當潤滑油參數及種類不同時，由式(7)和(8)可知，在相同的轉速以及荷載的情況下，滾動體與套圈之間形成的油膜厚度不一樣．通過選取不同油膜厚度，分析了油膜厚度對等效剛度的影響，得到了圖14油膜厚度與等效剛度的關系曲線．圖15為內圈轉速600 r/min、軸向荷載和徑向荷載為500 N時，油膜厚度與軸承振動的關系，縱坐標L表示軸承的振動加速度級．由圖可知，隨著油膜厚度的增大，軸承振動先減小后增大．油膜越薄時，油膜剛度越大，滾珠與套圈之間的受力區域變小，振動值增大；油膜越厚，油膜剛度越小，受力區域不穩定，振動值增大．因此軸承潤滑時，根據工況條件要合理控制油膜厚度，合理選取潤滑液.

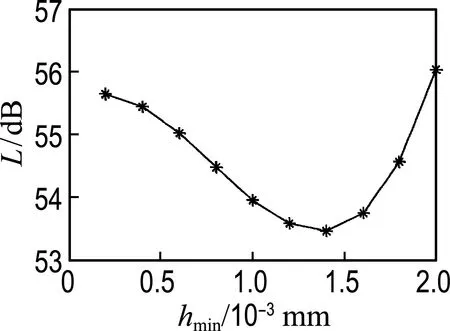
圖15 油膜厚度與軸承振動的關系Fig.15 The relationship between oil film thickness andnbearing vibration

4 結 論

(1)綜合考慮赫茲接觸剛度和潤滑接觸剛度的剛柔耦合多體接觸雙列深溝球軸承模型，其運動學及振動時頻域特性仿真與理論分析一致，可用于振動特性研究．

(2)合適的軸向與徑向荷載共同作用對雙列深溝球軸承的軸向振動和徑向振動均有抑制作用．

(3)隨著轉速的增加，雙列深溝球軸承振動加劇，呈近似線性關系．

(4)隨著油膜厚度的增大，雙列深溝球軸承振動先減小后增大．

(5)本文研究所得的雙列深溝球軸承振動與荷載、轉速、油膜厚度的關系曲線可作為其結構優化設計、減振降噪和運行狀態監測的參考依據．

[1]吳明星,吳 維,胡紀濱,等. 考慮自旋的高速角接觸球軸承油膜剛度計算[J]. 振動與沖擊, 2014, 33(10):38-42.

WU Mingxing, WU Wei, HU Jibin,etal. Oil film stiffness calculation of high speed angular contact ball bearings considering spinning [J]. Journal of Vibration and Shock, 2014, 33(10):38-42. (in Chinese)

[2]GUNDUZ A, SINGH R. Stiffness matrix formulation for double row angular contact ball bearings:Analytical development and validation [J]. Journal of Sound and Vibration, 2013, 332(22):5898-5916.

[3]鄧四二,董 曉,崔永存,等. 雙列角接觸球軸承動剛度特性分析[J]. 兵工學報, 2015, 36(6):1140-1146.DENG Si′er, DONG Xiao, CUI Yongcun,etal. Analysis of dynamic stiffness characteristics of double-row angular contact ball bearings [J]. Acta Armamentarii, 2015, 36(6):1140-1146. (in Chinese)

[4]張 剛,何永慧,張義民. 滾動軸承的多體接觸動力學仿真[J]. 振動、測試與診斷, 2013, 33(s1):28-31.ZHANG Gang, HE Yonghui, ZHANG Yimin. Multi-body contact dynamics simulation of rolling bearing [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(s1):28-31. (in Chinese)

[5]朱利軍,譚 晶,黃迪山,等. 基于ADAMS的深溝球軸承仿真分析[J]. 軸承, 2011, 2(2):3-6.

ZHU Lijun, TAN Jing, HUANG Dishan,etal. Simulation analysis of deep groove ball bearings based on ADAMS [J]. Bearing, 2011, 2(2):3-6. (in Chinese)

[6]李 昌,孫志禮. 基于彈流潤滑理論的深溝球軸承動態虛擬仿真[J]. 航空動力學報, 2009, 24(4):951-956.

LI Chang, SUN Zhili. Dynamic virtual simulation of deep groove ball bearing:based on elastohydrodynamic lubrication theory [J]. Journal of Aerospace Power, 2009, 24(4):951-956. (in Chinese)

[7]張 利,黃少成,徐 娟,等. 基于彈流潤滑理論的高速軸承動力學仿真分析[J]. 合肥工業大學學報(自然科學版), 2014, 37(5):516-519.

ZHANG Li, HUANG Shaocheng, XU Juan,etal. Dynamics simulation analysis of high-speed bearing based on elastohydrodynamic lubrication theory [J]. Journal of Hefei University of Technology (Natural Science), 2014, 37(5):516-519. (in Chinese)

[8]趙聯春, 馬家駒. 球軸承的彈性接觸振動 [J]. 機械工程學報, 2003, 39(5):60-64.

ZHAO Lianchun, MA Jiaju. Elastic contact vibrations of ball bearings [J]. Chinese Journal of Mechanical Engineering, 2003, 39(5):60-64. (in Chinese)

[9]袁 幸,朱永生,張優云,等. 基于模型辨識的滾動軸承故障診斷[J]. 振動、測試與診斷, 2013, 33(1):12-17.

YUAN Xing, ZHU Yongsheng, ZHANG Youyun,etal. Rolling element bearings fault diagnosis based on physical model identification [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1):12-17. (in Chinese)

[10]岡本純三. 球軸承的設計計算[M]. 黃志強,譯. 北京:機械工業出版社, 2003.

OKAMOTO J. Design Calculation of Ball Bearing [M]. HUANG Zhiqiang, trans. Beijing:China Machine Press, 2003. (in Chinese)

[11]HARRIS T A. Rolling Bearing Analysis [M]. 4th ed. New York:John Wiley & Sons Inc., 2000.

[12]SARANGI M, MAJUMDAR B C, SEKHAR A S. Stiffness and damping characteristics of lubricated ball bearings considering the surface roughness effect. Part 1:Theoretical formulation [J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2004, 218(6):529-538.

[13]陳於學. 基于接觸力學的圓柱滾子軸承振動研究[D]. 武漢:華中科技大學, 2005.

CHEN Yuxue. Research on vibrations of cylindrical roller bearings based on contact mechanics [D]. Wuhan:Huazhong University of Science & Technology, 2005. (in Chinese)

[14]HAMROCK B J, DOWSON D. Ball Bearing Lubrication:The Elastohydrodynamics of Elliptical Contacts [M]. New York:John Wiley & Sons Inc., 1981.

[15]林騰蛟,榮 崎,李潤方,等. 深溝球軸承運轉過程動態特性有限元分析[J]. 振動與沖擊, 2009, 28(1):118-122.

LIN Tengjiao, RONG Qi, LI Runfang,etal. Finite element analysis for dynamic characteristic of a deep-groove ball bearing in motion process [J]. Journal of Vibration and Shock, 2009, 28(1):118-122. (in Chinese)

[16]熊 濤,姚廷強,黃亞宇. 變速工況下球軸承-螺旋錐齒輪多體動力學分析[J]. 昆明理工大學學報(自然科學版), 2016, 41(1):57-63.

XIONG Tao, YAO Tingqiang, HUANG Yayu,etal. Multibody dynamic analysis of ball bearings-spiral bevel gear under variable speed condition [J]. Journal of Kunming University of Science and Technology (Natural Science Edition), 2016, 41(1):57-63. (in Chinese)

[17]邵毅敏,涂文兵. 深溝球軸承三維非線性時變振動特性研究[J]. 振動工程學報, 2013, 26(6):831-838.SHAO Yimin, TU Wenbing. 3D nonlinear time-varying vibration characteristics of deep-groove ball bearing [J]. Journal of Vibration Engineering, 2013, 26(6):831-838. (in Chinese)

Research on rigid-flexible coupling multi-body contact modeling and vibration characteristics of double-row deep-groove ball bearing

JIANG Lingli*1,2,BU Zhongjie1,HAN Qingkai1,2,LI Xuejun1

(1.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiangtan 411201, China；2.School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China )

A rigid-flexible coupling multi-body contact dynamics simulation model of double-row deep-groove ball bearing is proposed, which is based on analysis of the dynamic relationship among components of studied bearing through considering both the elastohydrodynamic lubrication theory and the Hertz contact theory, using the multi-body dynamics analysis software ADAMS combining flexible treatment by the finite element analysis software ANSYS. The equivalent stiffness is developed synthesizing the effect of Hertz contact stiffness and lubrication contact stiffness. The effects of different load, rotational speed and oil film thickness on the vibration characteristics of double-row deep-groove ball bearing are analyzed. The experimental results show that the adequate load can restrain the vibration of double-row deep-groove ball bearings, the increase of rotational speed can intensify the vibration, and the vibration decreases first, then increases with the increase of oil film thickness. The studied work can provide reference for structure optimization design, vibration and noise reduction and running state monitoring of double-row deep-groove ball bearing.

double-row deep-groove ball bearing; rigid-flexible coupling; elastohydrodynamic lubrication; contact stiffness; vibration characteristics

1000-8608(2017)04-0360-07

2016-08-08；

2017-04-14．

國家自然科學基金資助項目(51575177)；中國博士后科學基金資助項目(165246)；湖南省科技廳重點研發計劃資助項目(2015JC3108).

蔣玲莉*(1981-)，女，博士，副教授，E-mail:linlyjiang@163.com.

TH133.33

A

10.7511/dllgxb201704005