圈與路聯(lián)圖點可區(qū)別Ⅰ-全染色和點可區(qū)別Ⅵ-全染色

苗 婷 婷,王 治 文,陳 祥 恩*

(1.西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院， 甘肅 蘭州 730070；2.寧夏大學(xué) 數(shù)學(xué)計算機科學(xué)學(xué)院， 寧夏 銀川 750021 )

圈與路聯(lián)圖點可區(qū)別Ⅰ-全染色和點可區(qū)別Ⅵ-全染色

苗 婷 婷1,王 治 文2,陳 祥 恩*1

(1.西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院， 甘肅 蘭州 730070；2.寧夏大學(xué) 數(shù)學(xué)計算機科學(xué)學(xué)院， 寧夏 銀川 750021 )

一個圖G的Ⅰ-全染色是指若干種顏色對圖G的全體頂點及邊的一個分配使得任意兩個相鄰點及任意兩條相鄰邊被分配到不同顏色．圖G的Ⅵ-全染色是指若干種顏色對圖G的全體頂點及邊的一個分配使得任意兩條相鄰邊被分配到不同顏色．對圖G的一個Ⅰ(Ⅵ)-全染色及圖G的任意一個頂點x，用C(x)表示頂點x的顏色及x的關(guān)聯(lián)邊的顏色構(gòu)成的集合(非多重集)．如果f是圖G的使用k種顏色的一個Ⅰ(Ⅵ)-全染色，并且?u，v∈V(G)，u≠v，有C(u)≠C(v)，則稱f為圖G的k-點可區(qū)別Ⅰ(Ⅵ)-全染色，或k-VDITC(VDVITC)．圖G的點可區(qū)別Ⅰ(Ⅵ)-全染色所需最少顏色數(shù)目，稱為圖G的點可區(qū)別Ⅰ(Ⅵ)-全色數(shù)．利用組合分析法及構(gòu)造具體染色的方法，討論了圈與路的聯(lián)圖Cm∨Pn的點可區(qū)別Ⅰ(Ⅵ)-全染色問題，確定了這類圖的點可區(qū)別Ⅰ(Ⅵ)-全色數(shù)，同時說明了VDITC猜想和VDVITC猜想對于這類圖是成立的．

Ⅰ-全染色；點可區(qū)別Ⅰ-全染色；點可區(qū)別Ⅰ-全色數(shù)；圈與路的聯(lián)

0 引 言

點可區(qū)別正常邊染色、點可區(qū)別一般邊染色以及點可區(qū)別正常全染色分別在文獻(xiàn)[1-2]、[3-5]和[6-7]中被研究．文獻(xiàn)[8]討論了兩類點可區(qū)別的未必正常的全染色：點可區(qū)別Ⅰ-全染色和點可區(qū)別Ⅵ-全染色．本文在文獻(xiàn)[8]的基礎(chǔ)上討論圈與路的聯(lián)圖Cm∨Pn的點可區(qū)別Ⅰ-全染色和點可區(qū)別Ⅵ-全染色問題，確定這類圖的點可區(qū)別Ⅰ-全色數(shù)和點可區(qū)別Ⅵ-全色數(shù)，且證明VDITC猜想和VDVITC猜想對Cm∨Pn是成立的．

1 準(zhǔn)備工作

所謂圖G的全染色是指若干種顏色對于圖G的點及邊的一個分配．

對于圖G的一個全染色，如果任意兩個相鄰點有不同顏色，并且任意兩條相鄰邊有不同顏色，那么稱它為圖G的Ⅰ-全染色．

對于圖G的一個全染色，如果任意兩條相鄰邊有不同顏色，那么稱它為圖G的Ⅵ-全染色．

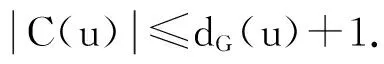
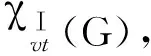
χⅠvt(G),

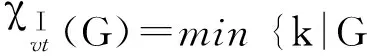
χⅠvt(G)=min{k|G

如果f是圖G的使用顏色1，2，…，k的一個Ⅰ-全染色，并且?u，v∈V(G)，u≠v，有C(u)≠C(v)，則稱f為圖G的k-點可區(qū)別Ⅰ-全染色，或k-VDITC．圖G的點可區(qū)別Ⅰ-全染色所需最少顏色數(shù)目，稱為圖G的點可區(qū)別Ⅰ-全色數(shù)，記為即有k-VDITC}．

χⅥvt(G),

χⅥvt(G)=min{k|G

如果f是圖G的使用顏色1，2，…，k的一個Ⅵ-全染色，并且?u，v∈V(G)，u≠v，有C(u)≠C(v)，則稱f為圖G的k-點可區(qū)別Ⅵ-全染色，或k-VDVITC．圖G的點可區(qū)別Ⅵ-全染色所需最少顏色數(shù)目，稱為圖G的點可區(qū)別Ⅵ-全色數(shù)，記為即有k-VDVITC}．

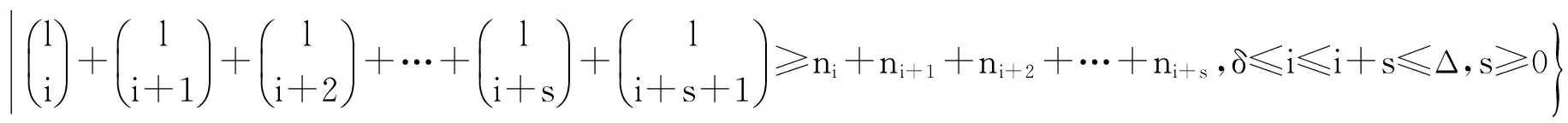
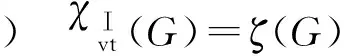
)χⅠvt(G)=ζ(G)

猜想1[8](VDITC猜想或ζ(G)+1．

)χⅥvt(G)=ζ(G)

猜想2[8](VDVITC猜想或ζ(G)+1．

引理1 對于任意圖G，如果存在兩個Δ(最大度)頂點，則

χⅠvt(G)≥Δ+1.

引理

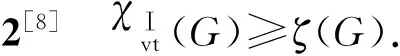
2[8]χⅠvt(G)≥ζ(G).

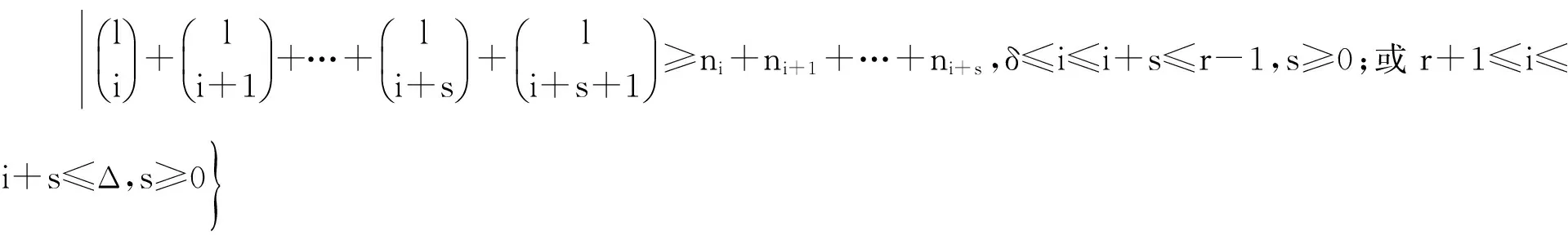
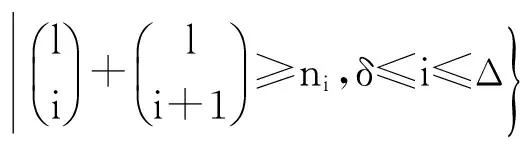
命題

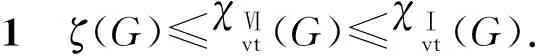
1ζ(G)≤χⅥvt(G)≤χⅠvt(G).

假設(shè)p∈Z，而q為正整數(shù)，用(p)q表示{1，2，…，q}中的模q同余于p的那個數(shù)，即(p)q∈{1，2，…，q}且(p)q≡p(modq)．

令V(Cm∨Pn)={u1，…，um，v1，…，vn}，E(Cm∨Pn)={u1u2，u2u3，…，um-1um，umu1，v1v2，v2v3，…，vn-1vn}∪{uivj|i=1，2，…，m；j=1，2，…，n}．

2 主要結(jié)果

定理1 設(shè)Cm∨Pn是圈Cm和路Pn的聯(lián)，m>n≥2，則

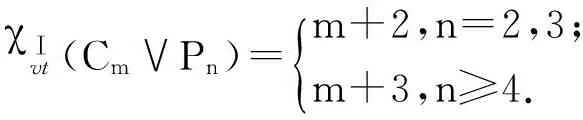
χⅠvt(Cm∨Pn)=m+2,n=2,3;m+3,n≥4.{

證明 當(dāng)n=2，m=3時，C3∨P2有5個m+1度的點，有5-VDITCf，其染色方式很容易得到．

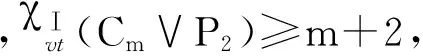
,χⅠvt(Cm∨P2)≥m+2,

當(dāng)n=2，m≥4時，Cm∨P2有兩個m+1度的點，m個4度點，由引理1知只需給出Cm∨P2的一個(m+2)-點可區(qū)別Ⅰ-全染色f．令

f(uivj)=i+j，f(uivj)∈{2，…,m+2}， 1≤i≤m，j=1，2；f(uiui+1)=i，i∈{2，…，m-1}；f(u1u2)=m+2，f(umu1)=1，f(v1v2)=1,f(v1)=1，f(v2)=3，f(u1)=2;f(ui)=i+2，i∈{2，…，m}

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(v1)={1，2，3，…，m+1}，C(v2)={1，3，4，…，m+1，m+2}；C(ui)={i-1，i，i+1，i+2}，i∈{3，…，m-1}；C(u1)={1，2，3，m+2}，C(u2)={2，3，4，m+2}，C(um)={m-1，m+1，m+2，1}

可見m+2個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

當(dāng)n=3，m=4時，C4∨P3有1個m+2度的點，有6-VDITCf，當(dāng)n=3，m=5時，C5∨P3有1個m+2度的點，有7-VDITCf，它們的染色方式容易得到，文中不詳細(xì)寫出．

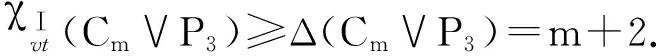
χⅠvt(Cm∨P3)≥Δ(Cm∨P3)=m+2.

f(uivj)=(i+j)m+2，f(uivj)∈{1，…，m+2}，1≤i≤m，j=1，2，3；f(uiui+1)=i，i∈{1，2，…，m-1}，f(umu1)=m，f(v1v2)=1，f(v2v3)=2；f(v1)=1，f(v2)=2，f(v3)=4，f(u1)=3，f(um)=m+1，f(ui)=i+3，i∈{2，…，m-1}

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(v1)={1，2，3，…，m+1}，C(v2)={1，2，3，…，m+1，m+2}，C(v3)={1，2，4，5，…，m+1，m+2}；C(ui)={i-1，i，i+1，i+2，i+3}，i∈{2，…，m-1}，C(u1)={1，2，3，4，m}，C(um)={m-1，m，m+1，m+2，1}

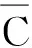
可見m+3個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

當(dāng)n≥4時有以下兩種情形需要考慮．

情形1m≥n+2

χⅠvt(Cm∨Pn)≥ζ(Cm∨Pn)=m+3.

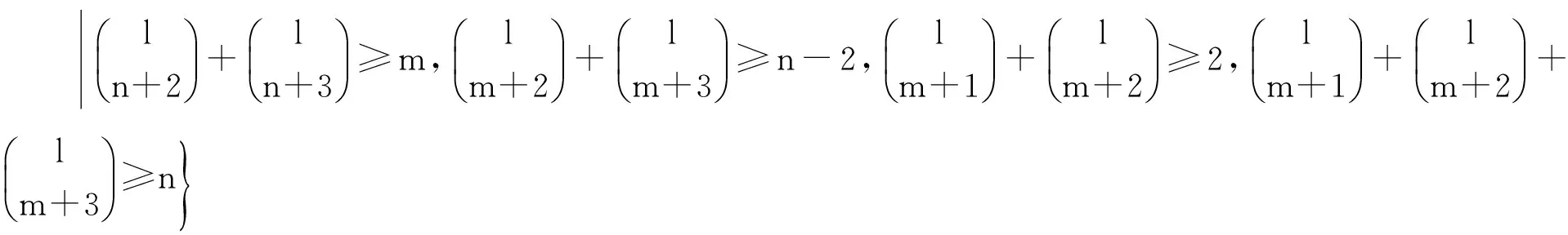
f(uivj)=(i+j)m+1，f(uivj)∈{1，2，…，m+1}，1≤i≤m，1≤j≤n；

f(vjvj+1)=m+2，j∈{1，2，…，n-1}，且j是奇數(shù)；f(vjvj+1)=m+3，j∈{1，2，…，n-1}，且j是偶數(shù)

f(uiui+1)=(i-1)m+1，i∈{1，2，…，m-1}；f(umu1)=m

f(ui)=i+1，f(ui)∈{2，…，m+1}，1≤i≤m

f(vj)=m+2，j∈{1，2，…，n}，且j是奇數(shù)；f(vj)=m+3，j∈{1，2，…，n}，且j是偶數(shù)

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(ui)={i+1，(i+2)m+1，…，(i+n)m+1，i-1，(i-2)m+1}，i≠1，m；C(u1)={2，3，…，n+1，m+1，m}，C(um)={m+1，1，2，…，n-1，m-2，m}，C(vj)={j+1，(j+2)m+1，…，(j+m)m+1，m+2，m+3}，j≠1；C(v1)={2，3，…，m+1，m+2}

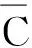
可見m+n個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

情形2m=n+1

χⅠvt(Cm∨Pn)≥ζ(Cm∨Pn)=m+3.

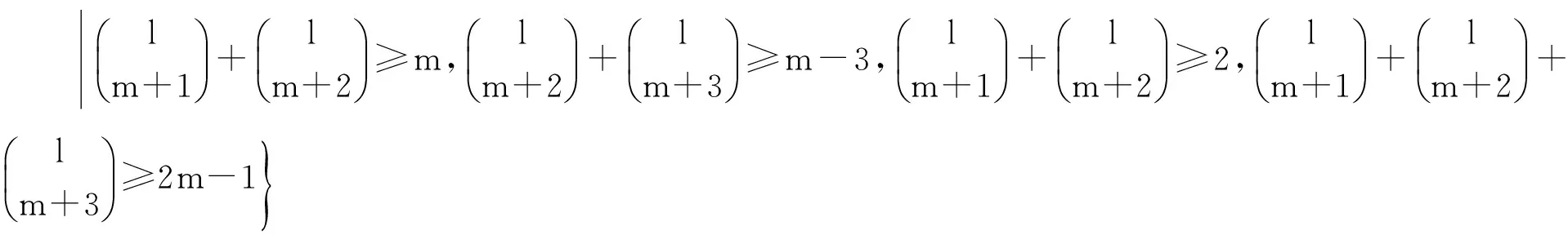
f(uivj)=(i+j)m+1，f(uivj)∈{1，2，…，m+1}，1≤i≤m，1≤j≤n；

f(uiui+1)=m+2，i∈{2，3，…，m-1}，且i是奇數(shù)；f(uiui+1)=m+3，i∈{2，3，…，m-1}，且i是偶數(shù)；當(dāng)m是偶數(shù)時，f(umu1)=m+3，f(u1u2)=m+2；當(dāng)m是奇數(shù)時，f(umu1)=m+2，f(u1u2)=1

f(vjvj+1)=m+2，j∈{1，2，…，n-1}，且j是奇數(shù)；f(vjvj+1)=m+3，j∈{1，2，…，n-1}，且j是偶數(shù)

f(ui)=i+1，f(ui)∈{2，…，m+1}，1≤i≤m

f(vj)=m+2，j∈{1，2，…，n}，且j是奇數(shù)；f(vj)=m+3，j∈{1，2，…，n}，且j是偶數(shù)

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(ui)={i+1，(i+2)m+1，…，(i+n)m+1，m+2，m+3}，i≠1，2；當(dāng)m為偶數(shù)時，C(u1)={2，3，…，m，m+2，m+3}，C(u2)={3，4，…，m+1，m+2，m+3}；當(dāng)m為奇數(shù)時，C(u1)={2，3，…，m，m+2，1}，C(u2)={3，4，…，m+1，m+3，1}；C(vj)={j+1，(j+2)m+1，…，(j+m)m+1，m+2，m+3}，j≠1；C(v1)={2，3，…，m+1，m+2}

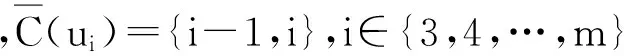
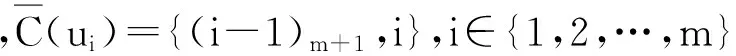
可見m+n個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

定理2 設(shè)Cm∨Pn是圈Cm和路Pn的聯(lián)，n>m≥3，則

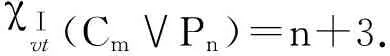
χⅠvt(Cm∨Pn)=n+3.

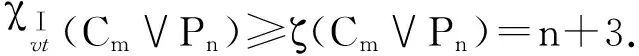
χⅠvt(Cm∨Pn)≥ζ(Cm∨Pn)=n+3.

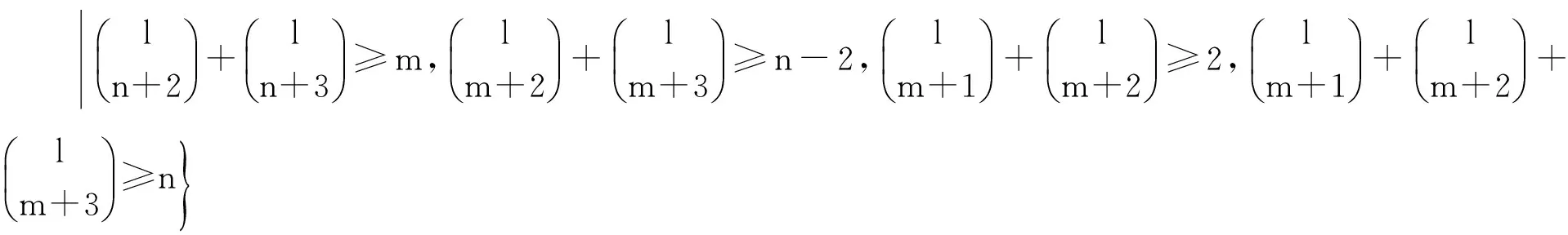
情形1m≡0(mod 2)．令

f(uivj)=(i+j-1)n+1，f(uivj)∈{1，2，…，n+1}，1≤i≤m，1≤j≤n

f(vjvj+1)=n+2，j∈{1，2，…，n-1}，且j是奇數(shù)；f(vjvj+1)=n+3，j∈{1，2，…，n-1}，且j是偶數(shù)

f(uiui+1)=n+2，i∈{1，2，…，m-1}，且i是奇數(shù)；f(uiui+1)=n+3，i∈{1，2，…，m-1}，且i是偶數(shù)；f(umu1)=n+3

f(ui)=i，f(ui)∈{1，2，…，m}，1≤i≤m

f(vj)=n+2，j∈{1，2，…，n}，且j是奇數(shù)；f(vj)=n+3，j∈{1，2，…，n}，且j是偶數(shù)

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(ui)={i，i+1，(i+2)n+1，…，(i+n-1)n+1，n+2，n+3}，1≤i≤m；C(vj)={j，j+1，(j+2)n+1，…，(j+m-1)n+1，n+2，n+3}，j≠1；C(v1)={1，2，3，…，m，n+2}

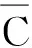
可見m+n個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

情形2m≡1(mod 2)．令

f(uivj)=(i+j-1)n+1，f(uivj)∈{1，2，…，n+1}，1≤i≤m-1，1≤j≤n；f(umvj)=(i+j+2)n+2，1≤j≤n

f(vjvj+1)=n+3，j∈{1，2，…，n-1}，且j是奇數(shù)；f(vjvj+1)=n+2，j∈{1，2，…，n-1}，且j是偶數(shù)

f(uiui+1)=n+2，i∈{1，2，…，m-1}，且i是奇數(shù)；f(uiui+1)=n+3，i∈{1，2，…，m-1}，且i是偶數(shù)；f(umu1)=n+1

f(ui)=i，f(ui)∈{1，2，…，m}，1≤i≤m

f(vj)=n+3，j∈{1，2，…，n}，且j是奇數(shù)；f(vj)=n+2，j∈{1，2，…，n}，且j是偶數(shù)

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(ui)={i，i+1，(i+2)n+1，…，(i+n-1)n+1，n+2，n+3}，i≠1，m；C(u1)={1，2，…，n，n+1，n+2}，C(um)={1，2，…，n-1，n+1，n+2，n+3}；C(vj)={j，j+1，(j+2)n+1，…，(j+m-2)n+1，j-1，n+2，n+3}，j≠1；C(v1)={1，2，…，m-1，n+2，n+3}

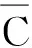
可見m+n個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

因此，不管哪種情形所得到的染色f都是Cm∨Pn的一個VDITC．

定理3 設(shè)Cn∨Pn是路Cn和圈Pn的聯(lián)，n≥3，則

χⅠvt(Cn∨Pn)=n+3,n=3,4;n+4,n≥5.{

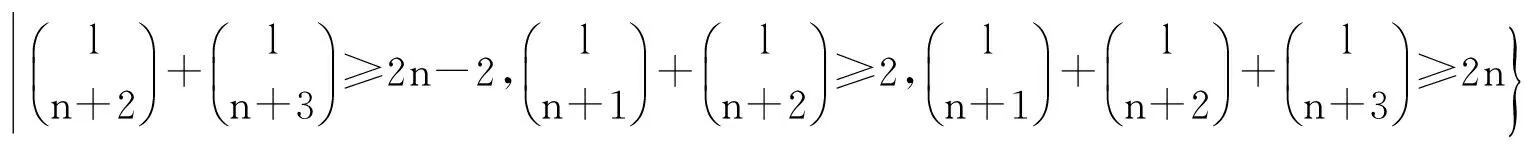
C3∨P3、C4∨P4的VDITC很容易得到，文中略去．

當(dāng)n=5時

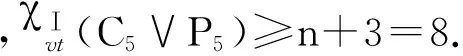
,χⅠvt(C5∨P5)≥n+3=8.

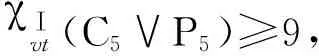
χⅠvt(C5∨P5)≥9,

故且C5∨P5的一個9-VDITC很容易得到，文中不詳細(xì)給出．

當(dāng)n=6時

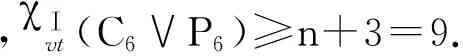
,χⅠvt(C6∨P6)≥n+3=9.

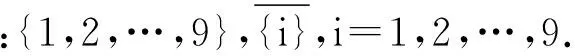
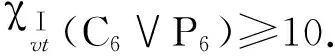
χⅠvt(C6∨P6)≥10.

故下面給出C6∨P6的一個10-VDITCf．令

f(uivj)=(i+j)10，f(uivj)∈{1，2，…，10}，1≤i≤6，1≤j≤6；f(u5v6)=3

f(uiui+1)=(i-1)10，i∈{1，2，…，5}，f(u6u1)=1；f(vjvj+1)=j，j∈{1，2，…，5}

點ui與vj染其關(guān)聯(lián)邊的顏色，其中ui染偶數(shù)色，vj染奇數(shù)色，并且相鄰點著不同色．特別地，f(v5)=1．

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(ui)={(i-2)10，i-1，i+1，(i+2)10，…，(i+6)10}，i∈{2，…，5}；C(u1)={1，2，…，7，10}，C(u6)={1，2，3，4，7，8，9，10}，C(vj)={j-1，j，j+1，(j+2)10，…，(j+6)10}，j∈{2，3，4}；C(v1)={1，2，3，…，6，7}，C(v5)={1，3，4，…，10}，C(v6)={1，2，5，7，…，10}

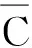
可見12個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

χⅠvt(Cn∨Pn)≥ζ(Cn∨Pn)=n+4.

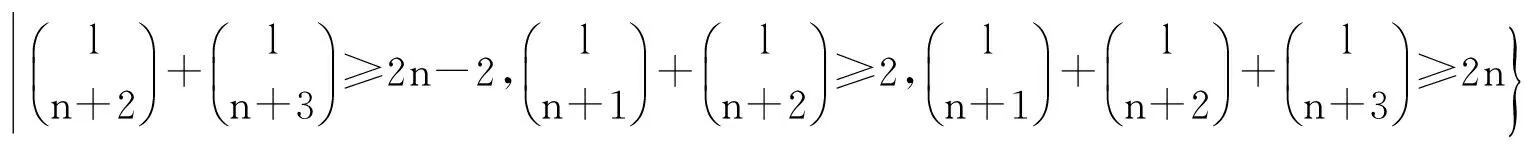
f(uivj)=(i+j-1)n+1，f(uivj)∈{1，2，…，n+1}，1≤i≤n，1≤j≤n

f(uiui+1)=n+2，i∈{1，2，…，n-1}，且i是奇數(shù)；f(uiui+1)=n+3，i∈{1，2，…，n-1}，且i是偶數(shù)；當(dāng)n為偶數(shù)時，f(unu1)=n+3；當(dāng)n為奇數(shù)時，f(unu1)=n+4

f(vjvj+1)=n+4，j∈{1，2，…，n-1}，且j是奇數(shù)；f(vjvj+1)=n+3，j∈{1，2，…，n-1}，且j是偶數(shù)

f(ui)=i，1≤i≤n；f(vj)=n+3，j∈{1，2，…，n}，且j是奇數(shù)；f(vj)=n+4，j∈{1，2，…，n}，且j是偶數(shù)

最終得到的上述全染色是Ⅰ-全染色，并且在此染色下有

C(ui)={i，i+1，(i+2)n+1，…，(i+n-1)n+1，n+2，n+3}，i≠1，n；當(dāng)n為偶數(shù)時，C(u1)={1，2，3，…，n，n+2，n+3}，C(un)={n，n+1，1，…，n-2，n+2，n+3}；當(dāng)n為奇數(shù)時，C(u1)={1，2，…，n，n+2，n+4}，C(un)={n，n+1，1，…，n-2，n+3，n+4}

C(vj)={j，j+1，(j+2)n+1，…，(j+n-1)n+1，n+4，n+3}，j≠n；當(dāng)n為奇數(shù)時，C(vn)={n，n+1，1，…，n-2，n+3}；當(dāng)n為偶數(shù)時，C(vn)={n，n+1，1，…，n-2，n+4}

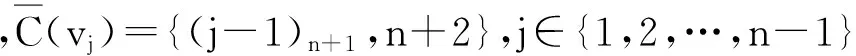
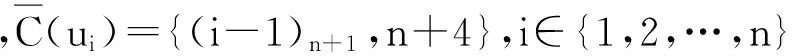
可見2n個點的色集合彼此互異，故上述Ⅰ-全染色是點可區(qū)別的．

定理4 若圖G是圈Cm與路Pn(m≥3，n≥2)的聯(lián)，則

χⅥvt(Cm∨Pn)=χⅠvt(Cm∨Pn).

由命題1知上述定理顯然成立．

3 結(jié) 語

,χⅥvt(Cn∨Pn)=χⅠvt(Cn∨Pn)=ζ(Cn∨Pn)+1,

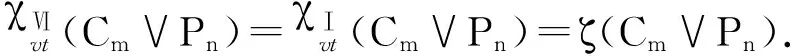
χⅥvt(Cm∨Pn)=χⅠvt(Cm∨Pn)=ζ(Cm∨Pn).

點可區(qū)別Ⅰ(Ⅵ)-全色數(shù)的確定和點可區(qū)別正常全色數(shù)的確定一樣，是困難的問題．目前缺少有效的方法和有力的工具，已得到的相關(guān)結(jié)論很少，并且其研究主要集中在具體圖上．通過本文的討論，可以看出VDITC猜想及VDVITC猜想對Cm∨Pn(m≥3，n≥2)是成立的：當(dāng)n=5，6時而對其他的Cm∨Pn有以后將繼續(xù)對圈和圈、圈和扇及圈和輪的聯(lián)圖的點可區(qū)別Ⅰ(Ⅵ)-全色數(shù)進(jìn)行研究．

[1]BURRIS A C, SCHELP R H. Vertex-distinguish proper edge-colorings [J]. Journal of Graph Theory, 1997, 26(2):73-82.

[2]BAZGAN C, HARKAT-BENHAMDINE A, LI Hao,etal. On the vertex-distinguish proper edge-colorings of graphs [J]. Journal of Combinatorial Theory, Series B, 1999, 75(2):288-301.

[3]HARARY F, PLANTHOLT M. The point-distinguishing chromatic index [M] //HARARY F, MAYBEE J S, Eds. Graphs and Application. New York:Wiley Interscience, 1985:147-162.

[5]CHEN Xiang′en. Point-distinguishing chromatic index of the union of paths [J]. Czechoslovak Mathematical Journal, 2014, 64(3):629-640.

[6]ZHANG Zhongfu, QIU Pengxiang, XU Baogen,etal. Vertex-distinguishing total colorings of graphs [J]. Ars Combinatoria, 2008, 87:33-45.

[7]CHEN Xiang′en, MA Yanrong. Vertex-distinguishing total colorings of 2Cn[J]. Chinese Quarterly Journal of Mathematics, 2013, 28(3):323-330.

[8]CHEN Xiang′en, LI Zepeng. Vertex-distinguishing Ⅰ-total colorings of graphs [J]. Utilitas Mathematica, 2014, 95:319-327.

Vertex-distinguishing Ⅰ-total colorings and vertex-distinguishing Ⅵ-total colorings of join-graph of cycle and path

MIAO Tingting1,WANG Zhiwen2,CHEN Xiang′en*1

(1.College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China；2.School of Mathematics and Computer Sciences, Ningxia University, Yinchuan 750021, China )

Ⅰ-total coloring of a graphGis an assignment of several colors to the vertices and edges of graphGsuch that any two adjacent vertices

ifferent colors and any two adjacent edges receive different colors. Ⅵ-total coloring of a graphGis an assignment of several colors to the vertices and edges of graphGsuch that any two adjacent edges receive different colors. For Ⅰ(Ⅵ)-total coloring of graphGand a vertexxof graphG,C(x) is used to denote the set (not multiset) composed of color ofxand colors of the edges incident withx. Letfbe Ⅰ(Ⅵ)-total coloring of a graphGusingkcolors andC(u)≠C(v) for any two different verticesuandvof graphG, thenfis called ak-vertex-distinguishing Ⅰ(Ⅵ)-total coloring of graphG, ork-VDITC (VDVITC) of graphGfor short. The minimum number of colors required in a VDITC (VDVITC) is the vertex-distinguishing Ⅰ(Ⅵ)-total chromatic number. The problems of vertex-distinguishing Ⅰ(Ⅵ)-total colorings of the join-graphCm∨Pnof cycle and path are discussed by the method of combinatorial analysis and constructing concrete coloring. Meanwhile, vertex-distinguishing Ⅰ(Ⅵ)-total chromatic numbers of graphCm∨Pnare determined. The results illustrate that the VDITC conjecture and VDVITC conjecture are valid for graphCm∨Pn.

Ⅰ-total coloring; vertex-distinguishing Ⅰ-total coloring; vertex-distinguishing Ⅰ-total chromatic number; join of cycle and path

1000-8608(2017)04-0430-06

2016-06-25；

2017-06-02．

國家自然科學(xué)基金資助項目(61163037，61163054，11261046，61363060)；寧夏回族自治區(qū)百人計劃資助項目.

苗婷婷(1991-)，女，碩士生，E-mail:miaotingting6130@163.com；陳祥恩*(1965-)，男，教授，碩士生導(dǎo)師，E-mail:chenxe@nwnu.edu.cn.

O157.5

A

10.7511/dllgxb201704015