一類復雜區域的網格優化算法

李 丹, 曹 敬

(河海大學 計算機與信息學院, 南京 210098)

?

一類復雜區域的網格優化算法

李 丹, 曹 敬

(河海大學 計算機與信息學院, 南京 210098)

近年來自由曲面設計得到了廣泛應用，尤其在建筑曲面設計領域。逼近自由曲面的方法有很多種，一種方法是采用平面四邊形網格(PQ網格)逼近自由曲面，所以平面四邊形網格的質量直接影響了自由曲面設計的質量。介紹了一種平面四邊形網格優化算法，判斷出復雜區域，采用局部采樣點加密和光順方法相結合進行處理，在整體上采用平面化和細分方法相結合策略優化網格。通過該方法，生成的自由曲面不僅質量得到了提高而且具有了美學效果。

自由曲面設計； 平面四邊形網格； 細分； 光順

0 引言

近年來,在自由曲面設計、三維動畫、計算機輔助幾何設計，真實感圖形繪制等領域,平面四邊形網格(PQ網格)得到了越來越多的應用。同三角網格較為自由的拓撲連接關系不同,四邊形網格的連接更為規則,并且根據實際的需要大都沿著主曲率方向分布,所以相比三角形網格更能反映網格所表示幾何形體的形狀變化,符合人們對形狀的自然感知。所以比三角形網格更為直接地應用在幾何造型、細分曲面、建筑設計等方面。所以生成有效且質量高的平面四邊形網格(PQ網格)非常重要。PQ網格的幾何性質和優化過程由KOBBEL.TOL[1]給出。根據以往研究知道具有PQ網格的自由曲面結構要優于具有三角形或非平面四邊形網格的自由曲面結構，所以平面四邊形網格具有研究價值。但是在以往的研究中，并沒有考慮四邊形網格的拐角或是皺痕部分等復雜區域，所以在本文中我們會著重處理四邊形網格的復雜區域。

PQ網格作為自由曲面設計的基礎具有很多的約束，不僅要求網格面是平面，還要符合一定的美學要求。在一些版本中，PQ網格也可以看作曲面上的共軛曲線網格，共扼曲線網格定義為曲面上的兩組單參數曲線v，w，它們在曲面上任意一個頂點x上的切向量互相共扼。這兩組切向量場構成了一個交叉場，我們稱之為共扼方向場。

對于四邊形網格的提取,我們采用Alliez等人[1]提出的各向異性四邊形網格化算法,在模型的各向異性區域,根據預定的采樣密度,逐條導出各向異性分布的主曲率線,據此生成各向異性四邊形網格,在球面或平面區域則均勻布點,生成三角形網格,最終得到各向異性的四邊形主導的主曲率網格。盡管得到的網格不能保證網格面是平面，但是至少是逼近平面的。像這樣的主曲率網格可以作為我們算法的輸入網格。

四邊形網格化是在曲面上生成四邊形網格的過程。利用曲面上的交叉向量場，追蹤曲線或全局參數化方法生成四邊形網格[2-11]。在本文中，我們采用從平滑的主曲率線提取四邊形網格的方法來生成四邊形主導的主曲率網格。

1.2 相關工作

平面四邊形網格化近年來已成為熱點，關于如何生成高品質的平面四邊形網格的研究很多。香港大學的劉等人[12]在ACM transactions on Graphics發表的Geometric Modeling with Concal Meshes and Developable Surfaces提出了從主曲率線中提取四邊形網格,擾動與細分相結合的算法獲得四邊形網格的平面性。

微軟亞洲研究院的劉等人[13]在ACM transactions on Graphics發表的General Planar Quadrilateral Mesh Design Using Conjugate Direction Field提出了允許存在k/4個奇點的共軛方向場(CDF)的研究。將自由曲面三角形離散化，計算滿足用戶方向和角度限制的近似平滑的共軛方向場，采用四邊形網格化和平面化技術相結合生成PQ網格。

德國亞琛工業大學的Bommes等人在ACM transactions on Graphics發表的Mixed-integer quadrangulation提出的保證交叉區域與主曲率線對齊，通過連續離散優化將四邊形網格和主曲率線對齊，得到了近似平面的網格。

1 平面化

1.1 平面性優化

(1)

另外，該算法引入兩個能量項確保得到的平面網格有光順的形狀。為了設計的美學要求，采用光順項ffair和f2nd，其簡化了網格的行和列的多邊形彎曲能量,為式(2)(3)。

(2)

(3)

在邊界上不是所有的點都需要計算，所以規定沒有定義的點的平方值設為零。PQ網格需要貼近原始網格Φ，因此要保證擾動的點與原始網格Φ的距離要最短,如式(4)。

(4)

其中，yi,j是網格Φ上關于原始點vi,j的優化后得到的點。

將以上所有項定義成Lagrangian函數為式(5)。

(5)

此時將平面化算法轉化成了非線性帶約束問題。

序列二次規劃法求w1ffair+w2f2nd+w3fclose的最小能量值，其中令約束cpq=0。也就是說最小值給出了一個PQ網格，其有一個光順的形狀并貼近原始網格。這個最小值是Lagrangian函數fpq的拐點，其中w1、w2和w3是用戶用來控制網格光順程度和質量的。

對于實際更新步長αh我們使用平滑的線性搜索算法得到，其中0<α≤1，x更新為x*=x+αh。

對于輸入的網格近似為共軛曲線網絡時，該算法的效果明顯。若輸入網格不理想時，則通過此算法優化的網格與原始網格有很大的偏差。所以輸入網格一般采用主曲率網格,如圖1所示。

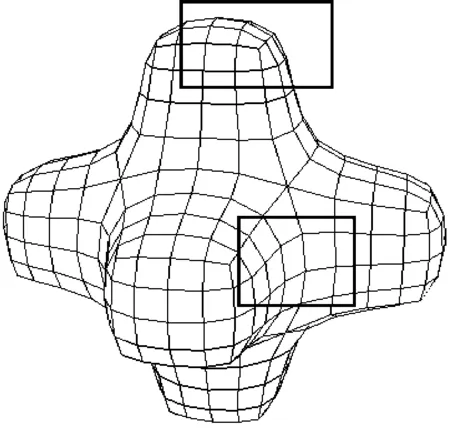
圖1 主曲率網格

圖1主曲率線四邊形網格應用PQ擾動，保證了幾乎所有的面都是平面四邊形。但是我們可以看出標出的四邊形網格平面性質量不是很好。

1.2 細分方法

對于細分算法我們選用Catmull-Clark細分。Catmull-Clark細分是最早提出的一種細分曲面算法。由于細分規則的簡單性和理論基礎的完備性，Catmull-Clark細分曲面至今仍是最受關注、應用最廣泛的細分曲面造型方法之一,如圖2所示。

(a)

(b)

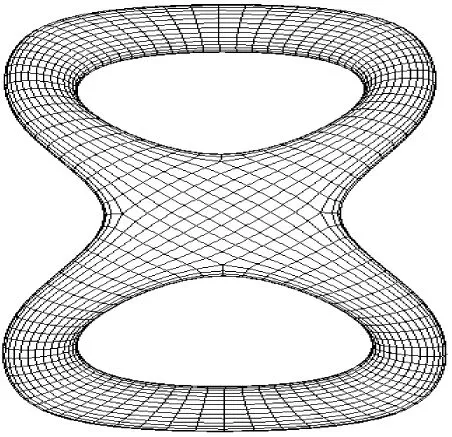
(c)

1.3 點鄰域平坦度計算

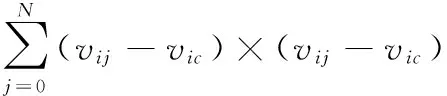
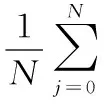
當k(vi)kε，vi點稱為復雜區域點，所在區域稱為復雜區域。在實驗中發現，kε=0.15能取得理想區域劃分。也是本文著重處理的區域。淺(黃)色區域即是我們需要處理的區域,如圖3所示。

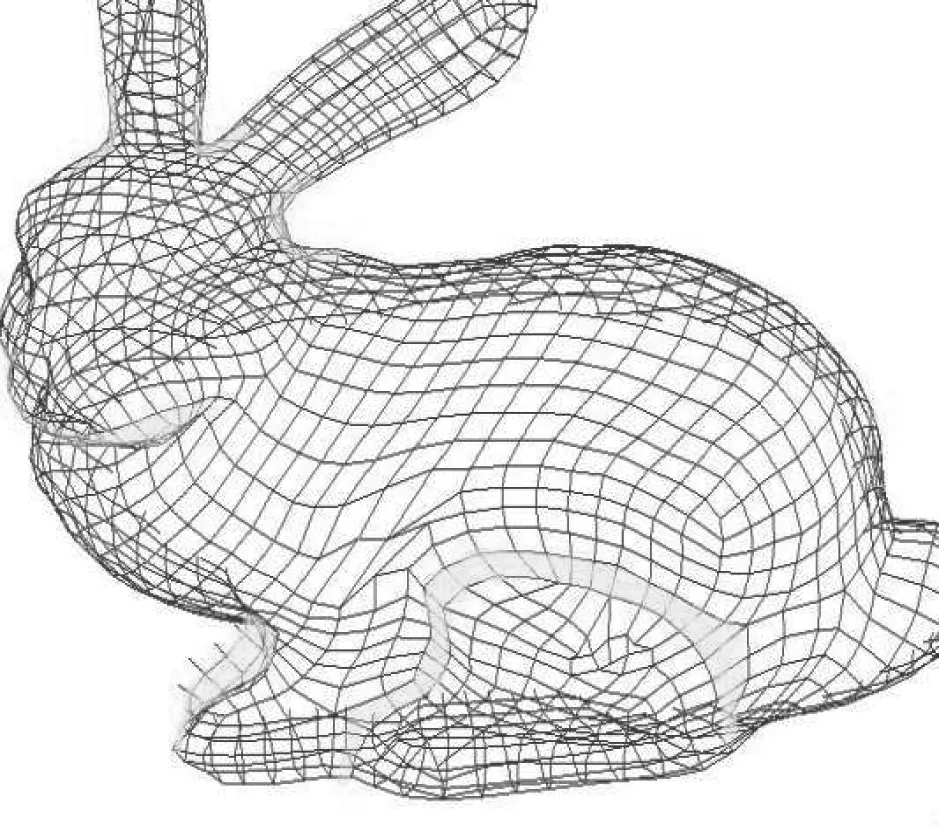
圖3

在一般情況下，復雜區域具有更高的噪音影響和更復雜的拓撲結構，平坦區域很容易實現網格的平面性等一些屬性，在曲率較大的復雜區域則很難得到同樣的效果。所以在復雜區域我們需要對每個點的鄰域進行細化，滿足原始網格特征的同時，也獲得該區域的平滑性和平面性。所以在復雜區域我們需要增加采樣點并且保證該區域的光順性，很自然地我們想到采樣點加密和光順相結合的策略。

本文采用類似浙江大學的王仁芳[15]提出的基于球面參數化的點模型漸變算法實現采樣點加密。首先對我們提取出的復雜區域模型進行球面參數化，使得參數化之后的模型嵌入到單位球面上，然后在球面上自適應地對齊模型間的相應特征點，并將球面映射到矩形參數域上，基于該域建立模型間采樣點的對應關系，采用拉普拉斯算子計算出中間點模型的幾何位置，最后利用移動最小二乘曲面進行動態采樣，實現采樣點加密。

對于光順方法我們采用清華大學的胡事民[16]提出的基于曲率流的四邊形主導網格的光順方法來實現,如圖4所示。

(a)初始網格(b)提取出的復雜區域(c)多次應用采樣點加密和光順算法得出的網格

圖4 光順方法

由此可以看出經過采樣點加密和光順算法的應用復雜區域有了明顯的改善。

2 細分與平面化結合

上文處理了復雜區域，在整體上我們采用Catmull-Clark細分方法和平面化算法相結合的策略，對網格模型進行平面化處理。首先完成初始網格的細分，細分的程度可根據情況而定。接下來是平面化。因為細分過程會破壞平面性，通過平面化算法又保證了平面性。此過程反復應用，直到達到所需的平面和細分程度,如圖5所示。

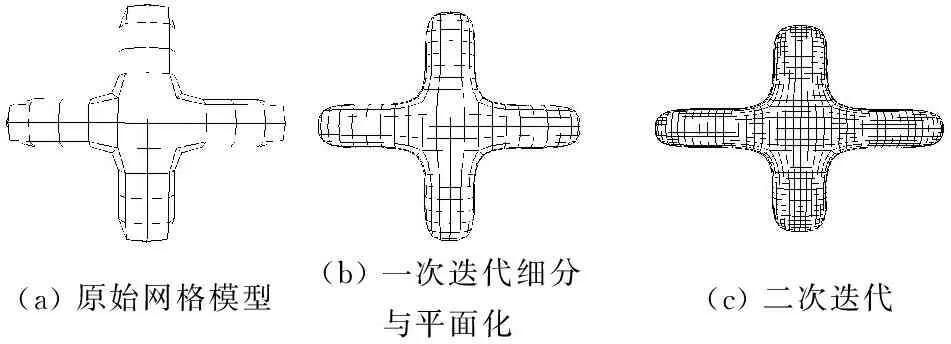
(a)原始網格模型(b)一次迭代細分與平面化(c)二次迭代

圖5 平面和細分程度

3 總結

相對于之前的不分區域的平面化和細分方法結合算法，在加入區域劃分之后的算法可以對網格質量有很好的提高.首先對復雜區域進行采樣點加密和光順，然后整體上應用細分與平面化相結合的策略滿足了網格模型的質量要求。但是若輸入網格不理想時，通過此算法優化的網格與原始網格有很大的偏差。所以在本文中我們選擇主曲率線網格。復雜區域不僅包括曲率較大區域，還包括奇異點鄰域。本文沒有考慮奇異點鄰域，這也是以后本文研究的重點。

[1] BOMMERS D., VOSSEMER T., KOBBELTo L. Quadrangular parameterization for reverse engineering[C]//Proc. of the MMCS 2008. LNCS 5862, 2010.

[2] ALLIEZ P.,COHEN-STEINER D.,DEVILLERS O.,et al.Anisotropic polygonal remeshing[J].ACM Trans. On Graphics,2003,22(3):485-493.

[3] MARINOV M.,KOBBELT L.Direct anisotropic quad-domint remeshing[C]//12th Pacific Conference on Computer Graphics and Applications.2004.

[4] RAY N.,LI W.,LEVY B.,et al.Periodic global parameterization[J].ACM Trans.on Graphics,2006,25(4):1460-1485.

[5] DONG S.,KIRCHER S.,GARLAND M.Hannonic functions for quadrilateral remeshing of arbitrary manifolds[J].Computer-Aided Geometrie Design.2005,22(4):292-423.

[6] TONG Y.,ALLIEZ P.,COHEN-STEINER D.,DESBRUN M.Designing quadrangulations with discrete hamonic forms[C]//Eurographics Symposium on Geometry Proeessing.2006.

[7] EBKE H.,BOMMES D.,CAMPEN M.,et al.Robust quad mesh extration[J].ACM Trans GraPh.2013,32(6):2504-2507.

[8] HUANG H.,ZHANG M.,MA J.,et al．Spectral Quadrangulation with Orientation and Alignment Control[J]．ACM Transactions on Graphics.2008,27(5),1-9.

[9] KALBERER F.,NIESER M.,POLTHIER K.Quadcover-surface parameterization using branched coverings[J]. Computer Graphics Forum, 2007, 26(3):375-384.

[10] BOMMES D., ZIMMER H., KOBBELT L.Mixed-Integer quadrangulation[J]. ACM Transactions on Graphics, 2009,28(3):1-10.

[11] LAI Y., KOBBELT L., HU S.An incremental approach to feature aligned quad dominant remeshing[C]//Proc. of the 2008 ACM Symp. on Solid and Physical Modeling. 2008.

[12] YANG Y.,LAI Y.,HU S.,et al.Robust principal curvaturesv on multiple scales[C]//Proceedings of 4th Eurographics Symposium on Geometry Processing Eurographics Association.2006.

[13] LIU L.,XU W.,WANG J.,et al.General Planar Quadrilateral Mesh Design Using Conjugate Direction Field[J].ACM Transactions on Graphics.2011,30(6), 140:1-140:10.

[14] LIU Y.,HELMUT P., WALLNER J.,et al.Geometric Modeling with Concal Meshes and Developable Surfaces[J].ACM Trans.Graphics.2006,25(3):681-689.

[15] 王仁芳,張三元,葉修梓.基于球面參數化的點模型漸變[J].中國圖象圖形學報,2009,14(3):552-559.

[16] 胡事民，來煜坤，楊永亮，基于曲率流的四邊形主導網格的網格方法[J].計算機學報,2008,31(9):1622-1628.

Mesh Optimization Algorithm for a Class of Complex Regions

Li Dan, Cao Jing

(College of Computer and Information, Hohai University, Nanjing 210098, China)

In recent years,freeform design has been widely used，especially in the field of architectural freeform design. There are many kinds of methods to approximate a freeform shape. One method is to approximate a freeform shape with a planar quadrilateral (PQ) mesh. So the quality of the PQ mesh directly affects the quality of the freeform shape design. This paper describes a planar quadrilateral mesh optimization algorithm. We first determine the complex regions, and combine up-sampling and fairing algorithms, then totally combine planar quad mesh with subdivision method. By this method, the freeform shapes not only improve the quality, but also have the aesthetic.

Freeform shape design; Planar quad mesh; Subdivision surface; Fairing

李 丹(1971-),男,碩士研究生，研究方向:計算機圖形學。 曹 敬(1968-)，男,工學博士，教授，研究方向:分布式處理及其軟硬件混同設計、網絡與信息安全等。

1007-757X(2017)07-0052-03

TP39

A

2016.12.20)