星間鏈路體制下的星地雙向時間同步方法

呂宏春，盧曉春，武建鋒

(1. 中國科學院國家授時中心，西安 710600；2. 中國科學院大學，北京 100049；3. 中國科學院精密導航定位與定時技術重點實驗室，西安 710600；4. 中國科學院大學天文與空間學院，北京 101408；5. 中國科學院大學電子電氣與通信工程學院，北京 101408)

?

星間鏈路體制下的星地雙向時間同步方法

呂宏春1,2,3，盧曉春1,3,4，武建鋒1,3,5

(1. 中國科學院國家授時中心，西安 710600；2. 中國科學院大學，北京 100049；3. 中國科學院精密導航定位與定時技術重點實驗室，西安 710600；4. 中國科學院大學天文與空間學院，北京 101408；5. 中國科學院大學電子電氣與通信工程學院，北京 101408)

推導了星地雙向時間同步的數學模型，提出了在星間鏈路體制下進行星地雙向時間同步的方法，計算了新一代導航試驗衛星與西安站的相對鐘差，通過對計算結果分別按1周、1天和1小時時長進行參數擬合，以及進行短期頻率穩定度分析，驗證了試驗階段星間鏈路體制下星地雙向時間同步的精度和性能。結果表明，1周、1天和1小時的擬合時長星間鏈路體制下的星地時間同步精度分別達到了3.42納秒、0.30納秒和0.15納秒，10000秒頻率穩定度優于8×10-14。

星間鏈路; 星地時間同步; 時分體制; 北斗衛星導航系統

0 引 言

建立星間鏈路(Inter-satellite link，ISL)，實現自主導航，主要目的就是支持GNSS持續進行高精度衛星星歷和鐘差估計，即定軌和時間同步，使導航系統在失去地面支持情況下具有一定的自主運行能力，同時解決我國北斗導航系統難以全球布站的問題[1]。我國從2015 年3月30號發射的新一代北斗導航衛星上開始增加了Ka頻段星間鏈路設備，開展星間鏈路工作。通過星間鏈路測量和時間同步可以得到衛星間的相對鐘差，將星地雙向時間同步技術應用于星間鏈路對地測量中可在星間鏈路體制下獲得星地鐘差。我國采用一種時分的星間鏈路體制，上下行鏈路同頻，在星地雙向時間同步中能消除電離層時延影響，有望獲得更高的星地時間同步精度。針對星間測量及時間同步需求，文獻[2]提出了一種動態環境下基于偽碼高精度距離測量和時間同步的技術，并通過仿真得到了厘米級的測距精度和優于1 ns的時間同步精度；文獻[3]以衛星雙向時間同步算法為基礎，針對衛星相對運行造成星間距離變化特點，提出了一種衛星動態雙向時間同步算法，仿真得到了優于5 ns的精度；文獻[4]針對相對論效應對星間測量的影響，提出了帶有相對論效應修正的雙向單程測距與時間同步算法。

傳統的星地雙向時間同步技術已成功應用于北斗區域衛星導航系統(北斗二號)衛星鐘差的測量，國內對星地雙向時間同步方法已有較多研究，文獻[5]建立了用于星地雙向時間同步的模型，并通過試驗數據獲得平均約0.34 ns的擬合精度；文獻[6]將星地雙向時間同步技術應用于北斗衛星試驗階段，得到1 ns單弧段擬合精度；文獻[7]在星地測量中考慮衛星運動因素，提出了一種基于最小二乘擬合的星地動態雙向時間同步和測距算法，可有效消除衛星運動對雙向時間同步和測距的不利影響。

傳統的星地雙向時間同步技術不能直接應用于星間鏈路的對地鏈路，本文針對星間鏈路時分體制下星地鏈路的特點，對時分觀測的雙向單程偽距進行歷元歸算，推導星地雙向時間同步數學模型，對星間鏈路體制下的星地雙向時間同步方法進行研究，驗證了試驗階段星間鏈路體制下星地雙向時間同步的精度。

1 星間鏈路體制下的星地雙向時間同步原理和數學模型

1.1 傳統星地雙向時間同步方法

傳統的星地雙向時間同步中衛星和地面站在相等的鐘面時互發信號[8]，雙向單程偽距為：

(1)

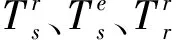
(2)

(3)

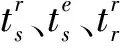
(4)

對系統時的計算需要衛星、地面鐘差模型支持，此處可以使用預報鐘差模型代替，也可暫以鐘面時代替，待求解出鐘差模型后再代入式(4)重新計算。

偽距觀測量以本地時鐘的信號接收時刻記錄，則信號發射時刻為：

(5)

鐘差是時變的，由于光行時影響，在信號傳播過程首末的鐘差有所差異。GEO和IGSO衛星軌道高度35786km，MEO衛星軌道高度21528km，則GEO和IGSO星地測距中的光行時約為0.12s，MEO星地測距中的光行時約為0.07s。統計2015年11月全部在軌GPS衛星和北斗衛星的鐘速，結果表明除北斗C05和C14外其余衛星鐘速絕對值均小于5×10-11。則以GEO衛星為例，由光行時引起的信號傳播過程首末衛星鐘差差值小于0.006ns，對于0.1ns量級的時間同步精度而言可以忽略不計；C05鐘速絕對值達到約4×10-10，由此帶來的衛星鐘差差值約0.048ns，對于0.1ns量級的時間同步精度不可忽略。顧及鐘速絕對值較大的情況，在星地雙向時間同步過程中需要考慮由于光行時引起的信號傳播過程首末衛星鐘差的變化，同理也應考慮地面站鐘差的變化。

傳統的星地雙向時間同步中衛星和地面站在相等的鐘面時互發信號，將星地雙向單程測量中衛星鐘差、地面鐘差分別記作 ΔTs和ΔTr，則

(6)

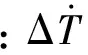
(7)

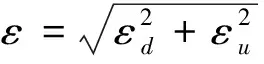
由于上下行偽距近似相等，則式(7)可改寫為：

(8)

由于上下行鏈路近似對稱，衛星星歷誤差、地面坐標誤差及信號傳播過程中的對流層時延等公共誤差項將削弱或抵消，這是雙向時間比對能獲得高精度的主要原因。雙向時間同步的核心策略即是盡量保證上下行鏈路的對稱性，對造成非對稱的諸如電離層時延、Sagnac效應、光行差、通道時延等項進行修正。利用衛星星歷分別計算各衛星在相應系統時的坐標，可以修正光行差；對通道時延可提前進行標定并扣除；對Sagnac效應既可針對衛星或地面站坐標進行修正[9]，也可以直接修正其造成的路徑方向延遲[10]；在傳統的星地雙向時間同步中上下行鏈路不同頻，導致上下行電離層時延不同，需使用電離層時延修正模型進行修正。

相對論效應τrel可以利用衛星星歷參數或者三維坐標及速度矢量通過公式準確計算，方法如式(9)所示[11-12]：

(9)

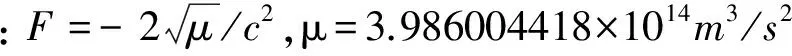
也可用式(10)形式：

(10)

式中：R和V分別表示衛星瞬時三維坐標及速度矢量。

星地雙向時間同步得到的結果為星地相對鐘差值，已知地面鐘差可得到衛星鐘差。不同頻點、不同系統之間可能存在零值偏差，需要對包含設備通道時延在內的零值偏差進行標校。

1.2 星地雙向時間同步方法在星間鏈路體制的應用方式

在星間鏈路體制中雙向單程偽距測量值并不是在相同鐘面時互發信號，而是采用一種時分體制，即一個時隙完成衛星發射信號以及地面接收信號的過程，下一個時隙完成地面發射衛星接收的過程。為將星地雙向時間同步方法應用于星間鏈路體制，必須首先對雙向偽距觀測量的歷元進行歸算，使雙向單程偽距歸算到同一觀測歷元。在傳統的星地雙向時間同步中，星地雙方在同一鐘面時互發信號，從而保證了路徑的近似對稱性，星間鏈路體制下可以將雙向單程偽距觀測量歸算到同一鐘面時互收信號，也保證了路徑的近似對稱性。對已進行歷元歸算的星地雙向偽距觀測量可按照傳統的星地雙向時間同步方法進行計算。

可使用多項式插值的方法實現歷元歸算，多項式插值法直接以偽距觀測值為插值節點，對歷元歸算時刻進行插值計算。拉格朗日插值是多項式插值的典型代表，n階拉格朗日插值函數定義為[13]：

(11)

式中：xk和yk組成插值基節點對，對于偽距插值而言xk為插值節點時刻，yk為插值節點時刻對應的偽距值；x為待插值歷元；則對應的函數值fn(x)就是插值結果。拉格朗日插值的階數n與插值基節點個數m的關系為：m=n+1。

插值精度與觀測值的采樣間隔及多項式階數有關，以1分鐘間隔的偽距觀測值為例，4～6階拉格朗日插值即可獲得優于1mm的插值精度。

在星間鏈路體制下，星地上下行鏈路信號頻率相同，對于已經進行了歷元歸算的星地雙向偽距觀測值，基本可抵消上下行鏈路的電離層時延。

2 試驗分析

在2015年11月15日至2015年11月21日(即北斗515周)使用I1S衛星與西安站進行星間鏈路體制下的星地雙向偽距測量，共得到6d的有效數據(2015年11月21日西安站地面設備未參與試驗)。

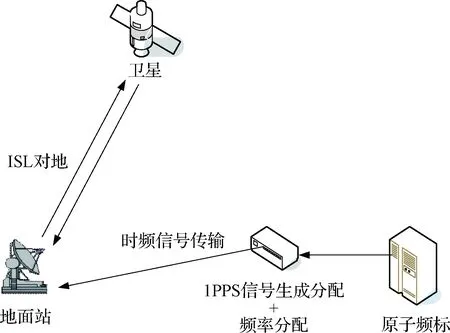
圖1 試驗系統示意圖Fig.1 Sketch map of test system

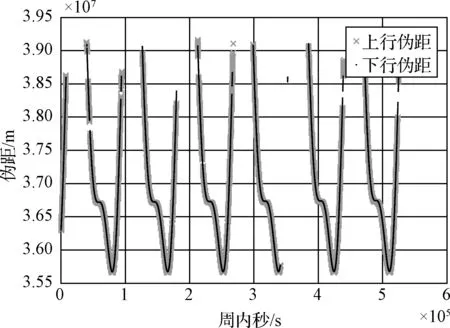
圖2 原始觀測數據Fig.2 Original pseudorange observations

圖1為試驗系統示意圖，地面站時鐘信號由原子頻標提供，衛星與地面站通過星間鏈路體制下的對地測量鏈路實現星地雙向偽距測量。原始偽距觀測數據如圖2所示。

將星地雙向時間同步方法用于星間鏈路體制中進行鐘差計算，利用零值標校手段扣除星間鏈路設備時延后，與同時段的L波段對該衛星的星地雙向時間同步結果進行比較，結果如圖3所示。

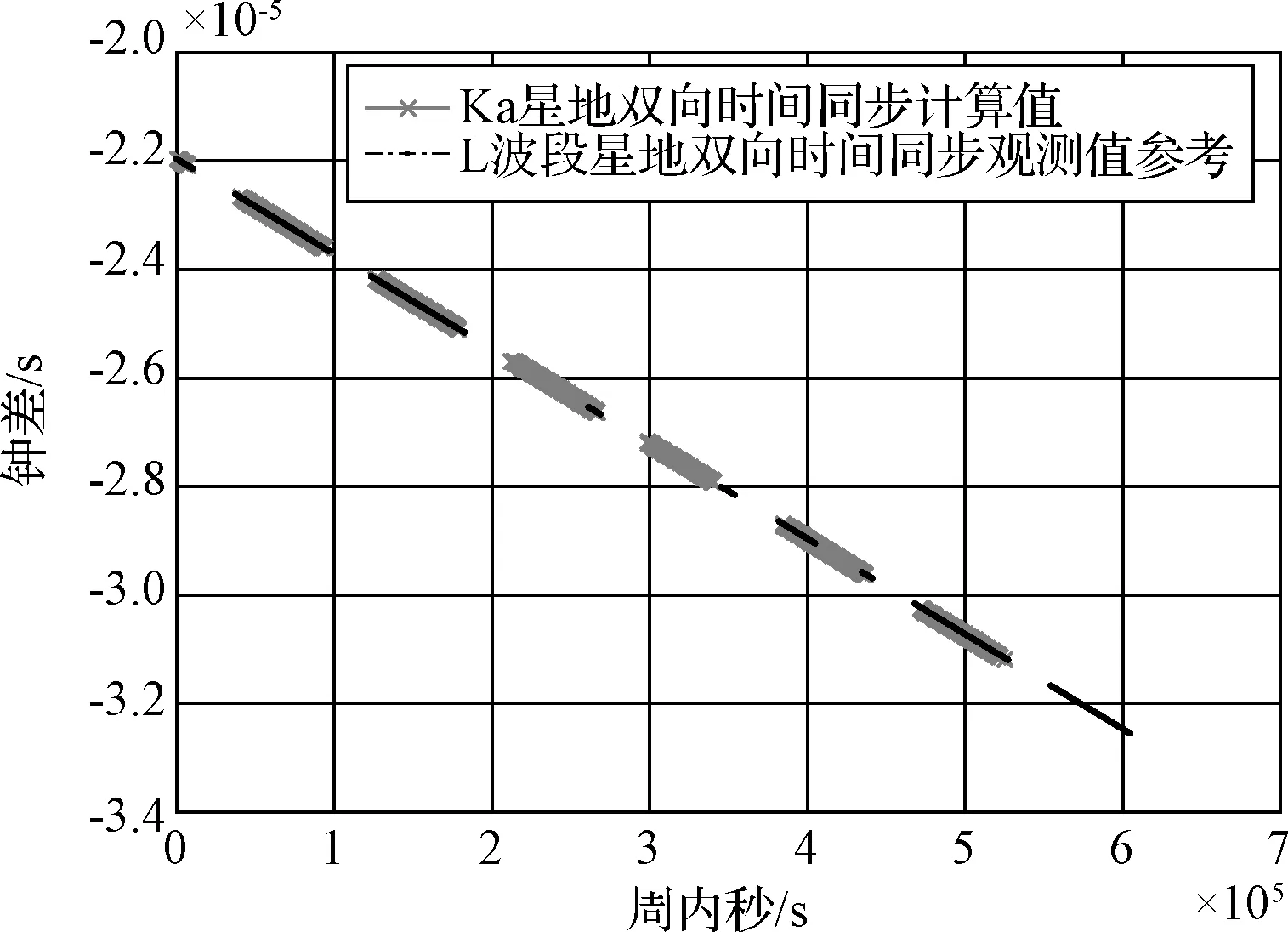
圖3 ISL星地鐘差與L波段星地鐘差Fig.3 Satellite-ground clock offset of ISL and L band

星地時間同步精度常使用擬合殘差來表征，由于擬合殘差結果與擬合時長存在較大關聯，本文分別計算1周、1天和1小時時長弧段的擬合殘差，分析時間同步性能。

對ISL體制下的星地雙向時間同步結果按1周弧段時長進行二次三項式擬合，并與同時段L波段雙向時間同步的結果的擬合殘差對比，擬合殘差見圖4。

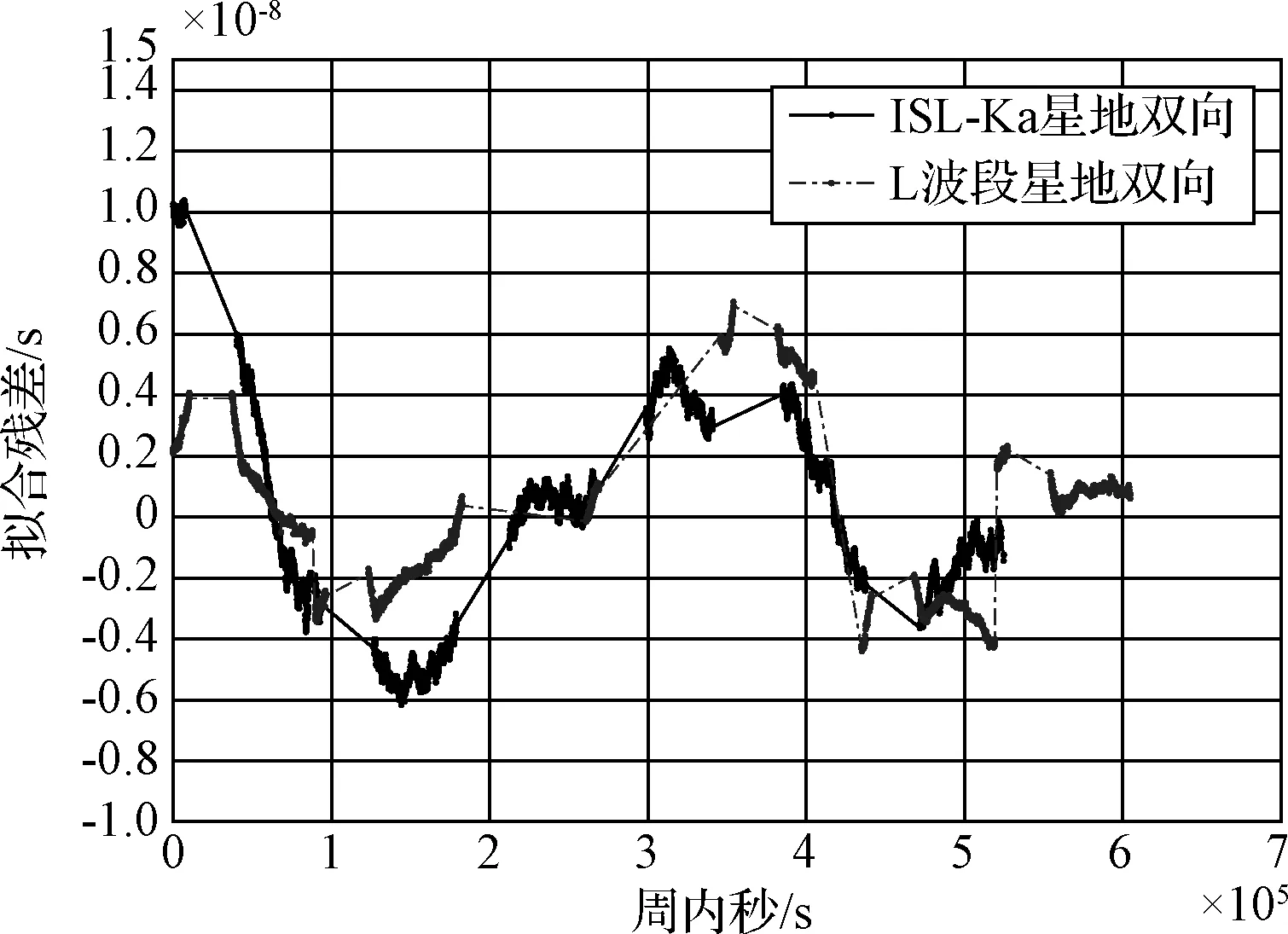
圖4 1周時長擬合殘差Fig.4 One week time length fitting residuals

對于1周時長的擬合，ISL體制下的星地雙向時間同步結果與L波段雙向時間同步結果的擬合殘差的RMS分別為3.42ns和2.66ns，L波段雙向時間同步結果略優于ISL對地比對結果；二者鐘速差為-7.4×10-14，以L波段計算結果為參考值，得到ISL體制下的星地雙向時間同步結果與L波段計算結果的偏差RMS為1.59ns。結果表明對于1周時長的擬合，ISL體制下的星地雙向時間同步結果與L波段結果符合的較好。

計算觀測時段較完整的兩天的星地雙向時間同步結果，并進行1天時長二次三項式擬合，第1天和第2天弧段的結果分別如圖5和圖6所示。結果表明，對第1天整弧段進行擬合時，ISL體制下的星地雙向時間同步結果約在-1.0ns～1.0ns之間波動，擬合殘差RMS約為0.5ns；第2天弧段計算結果多在-0.5ns～0.5ns之間波動，擬合殘差RMS約0.3ns。

對第1天和第2天的ISL體制下的星地雙向時間同步結果每1小時進行一次二項式擬合，得到擬合結果分別如圖7和圖8所示，ISL體制下弧段1的星地雙向時間同步結果擬合殘差為0.21ns，弧段2為0.15ns.

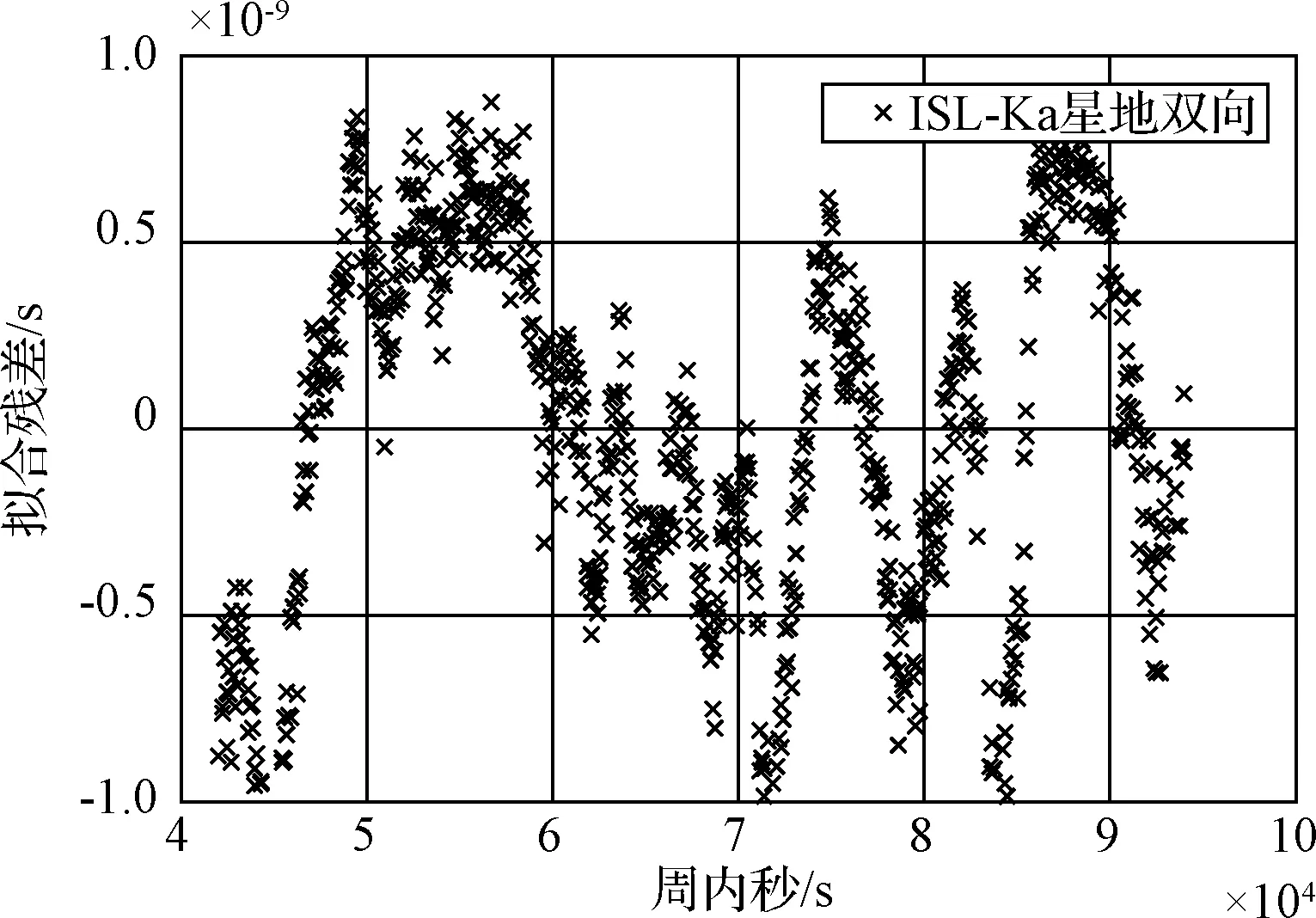
圖5 第1天弧段1天時長擬合殘差Fig.5 One day time length fitting residuals for the 1st day

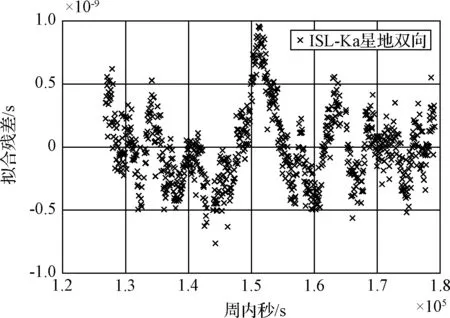
圖6 第2天弧段1天時長擬合殘差Fig.6 One day time length fitting residuals for the 2nd day

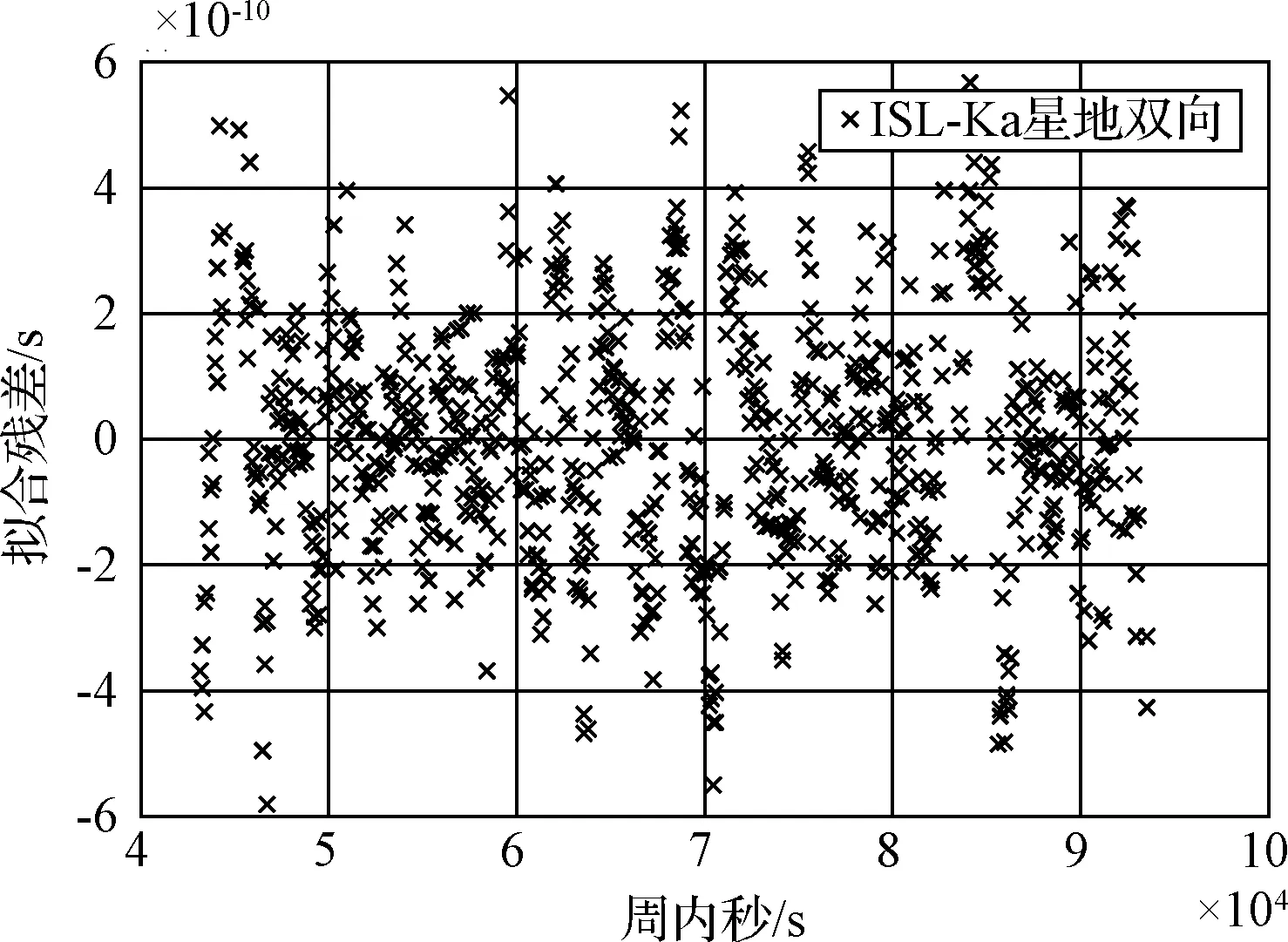
圖7 第1天弧段1小時擬合時長擬合殘差Fig.7 One hour time length fitting residuals for the 1st day

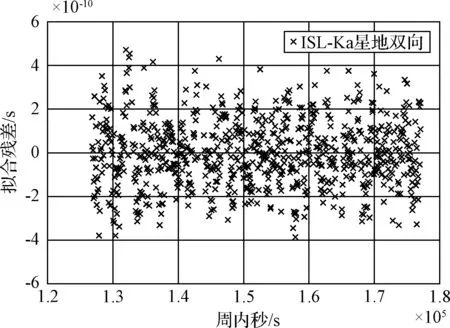
圖8 第2天弧段1小時擬合時長擬合殘差Fig.8 One hour time length fitting residuals for the 2nd day

對ISL體制下星地雙向時間同步中的第1天弧段和第2天弧段的下行偽距和上行偽距分別分段進行高階多項式擬合，第1天弧段下行偽距擬合殘差RMS為0.053m，上行偽距擬合殘差RMS為0.034m，如圖9所示；第2天弧段下行偽距擬合殘差RMS為0.055m，上行偽距擬合殘差RMS為0.034m，可近似表征上下行測量噪聲。則對上下行噪聲進行合成，得到第1天弧段合成噪聲約0.031m，對鐘差的影響約為0.10ns，第2天弧段合成噪聲約0.032m，對鐘差的影響約0.11ns。將合成噪聲分別與第1天和第2天的ISL體制下的星地雙向時間同步結果按1小時擬合時長擬合的殘差進行比較，可知本例中ISL體制下的星地雙向時間同步結果擬合殘差均大于合成噪聲，其中第1天弧段的擬合殘差超過合成噪聲約0.11ns，第2天弧段的擬合殘差略大于合成噪聲，超過合成噪聲約0.04ns，表明第1天弧段含有更大的系統誤差。

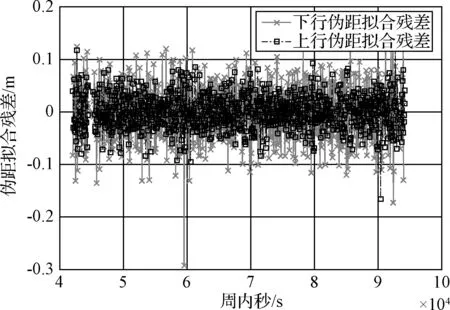
圖9 第1天弧段偽距擬合殘差Fig.9 Fitting residuals of pseudorange for the 1st day

為進一步分析ISL體制下的星地雙向時間同步結果性能，計算第1天弧段和第2天弧段結果的阿倫方差，進行短期頻率穩定度分析，結果如圖10所示。第1天弧段和第2天弧段100s、1000s和1000s的頻率穩定度見表1。

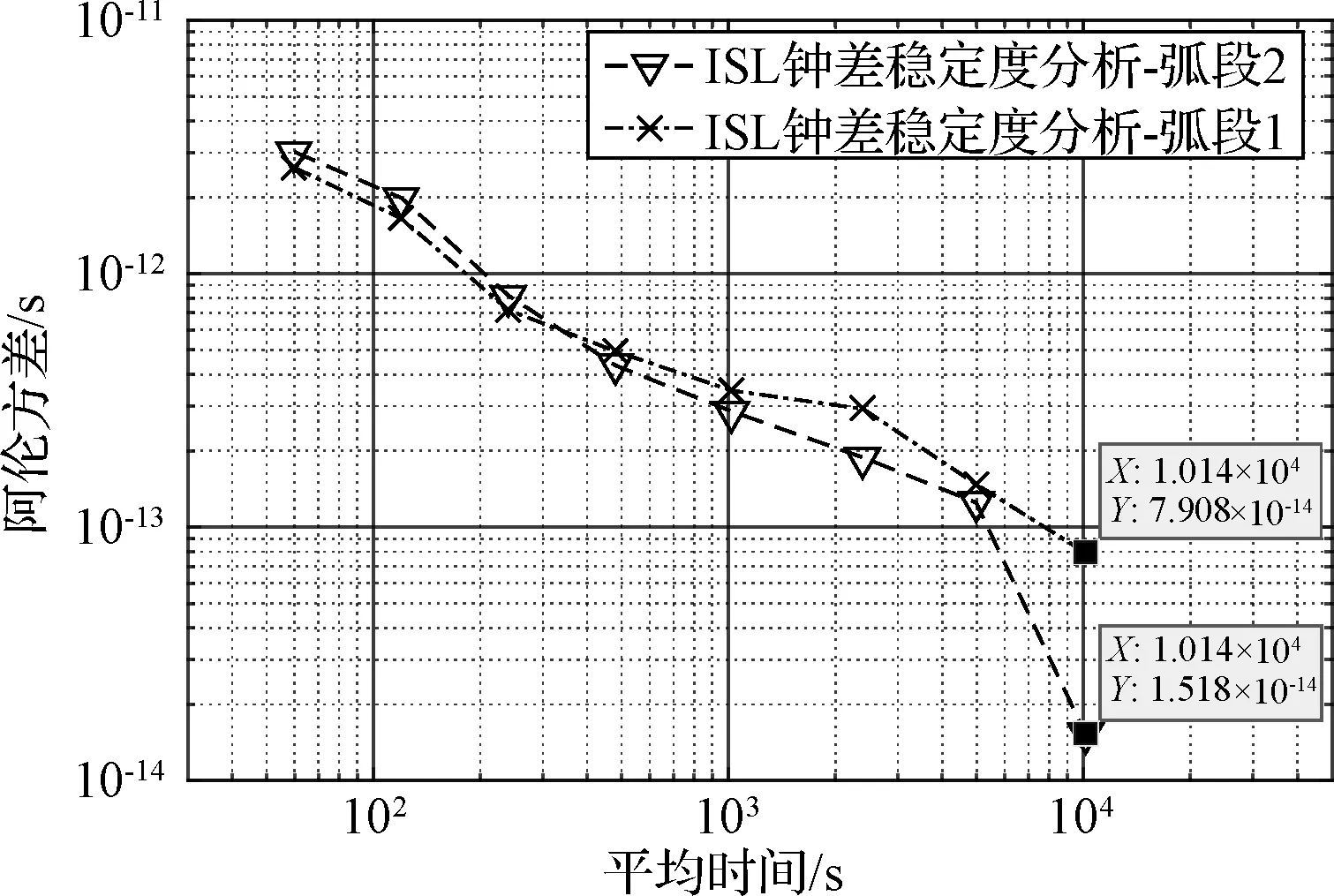
圖10 星間鏈路體制下星地雙向時間同步結果的頻率穩定度分析Fig.10 Frequency stability of satellite-ground two-way time synchronization under ISL system

弧段100s1000s10000s第1天1．6×10-123．5×10-137．9×10-14第2天2．0×10-122．9×10-131．5×10-14

目前北斗2號衛星星地雙向時間同步計算值短期頻率穩定度[14]中10000s穩約為1×10-13，與之相比本文針對I1S衛星ISL體制下的星地雙向時間同步結果較優；經過載波相位方法計算得到的北斗2號衛星鐘差的頻率穩定度[15]的10000s穩為4.3×10-14～1.5×10-13，與之相比ISL體制下星地雙向時間同步結果的10000s穩定度在同一量級。結果表明ISL體制下星地雙向時間同步結果的10000s穩優于8.0×10-14，最優可達1.5×10-14。

3 結 論

本文推導了星間鏈路體制下的星地雙向時間同步數學模型，計算了在軌試驗期間I1S衛星與地面站的相對鐘差，并對計算結果分別按1周、1天和1小時時長進行參數擬合，最后進行短期頻率穩定度分析，依據有限的數據計算結果，主要有以下結論：

1)對于1周擬合時長，ISL體制下的星地雙向時間同步結果的擬合精度達3.42ns，與L波段結果的鐘速差為-7.4×10-14，二者擬合殘差具有一致性；

2)對于1天擬合時長，ISL體制下的星地雙向時間同步結果能達到約0.30ns的擬合精度；

3)對于1小時擬合時長，ISL體制下的星地雙向時間同步結果能達到約0.15ns的擬合精度；

4)分析ISL體制下的星地雙向時間同步結果的短期穩定度，結果表明其10000s穩定度優于8×10-14。

[1] 王冬霞, 辛潔, 薛峰, 等.GNSS星間鏈路自主導航技術研究進展及展望[J]. 宇航學報, 2016, 37(11): 1279-1288. [WangDong-xia,XinJie,XueFeng,etal.DevelopmentandprospectofGNSSautonomousnavigationbaseoninter-satellitelink[J].JournalofAstronautics, 2016, 37(11): 1279-1288.]

[2] 黃波, 胡修林. 北斗 2 導航衛星星間測距與時間同步技術[J]. 宇航學報, 2011, 32(6): 1271-1275. [HuangBo,HuXiu-lin.Inter-satelliterangingandtimesynchronizationtechniqueforBD2[J].JournalofAstronautics, 2011, 32(6): 1271-1275.]

[3] 黃飛江, 盧曉春, 吳海濤, 等. 基于星間距離變化的動態雙向時間同步算法[J]. 武漢大學學報: 信息科學版, 2010,35(1): 13-16. [HuangFei-jiang,LuXiao-chun,WuHai-tao,etal.Analgorithmofdynamictwo-waytimetransferbasedoninter-satelliterangevariation[J].GeomaticsandInformationScienceofWuhanUniversity, 2010,35(1): 13-16.]

[4] 孫文超, 常青, 徐勇, 等. 星間DOWRT中的相對論效應分析與修正[J]. 北京航空航天大學學報, 2012, 38(3): 335-339. [SunWen-chao,ChangQing,XuYong,etal.Analysisandcorrectiononrelativisticeffectofinter-satellitesusingdualone-wayranging/timesynchronization[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2012, 38(3): 335-339]

[5]LiuL,ZhuLF,HanCH,etal.Themodelofradiotwo-waytimecomparisonbetweensatelliteandstationandexperimentalanalysis[J].ChineseAstronomyandAstrophysics, 2009, 33(4): 431-439.

[6] 李瑞鋒, 王元明. 星地雙向時間同步技術在COMPASS中的應用[J]. 武漢大學學報: 信息科學版, 2013, 38(7): 842-844. [LiRui-feng,WangYuan-ming.Applicationoftwo-waysatellite-groundtimesynchronizationinCOMPASS[J].GeomaticsandInformationScienceofWuhanUniversity, 2013, 38(7): 842-844]

[7] 黃飛江, 盧曉春, 劉光燦,等. 星地動態雙向時間同步與測距算法[J]. 宇航學報, 2014, 35(9):1050-1057. [HuangFei-jiang,LuXiao-chun,LiuGuang-can,etal.Analgorithmfordynamicsatellite-groundtwo-waytimesynchronizationandranging[J].JournalofAstronautics. 2014, 35(9):1050-1057].

[8]ChunhaoH,ZhiwuC,YutingL,etal.TimesynchronizationandperformanceofBeiDousatelliteclocksinorbit[J].InternationalJournalofNavigationandObservation, 2013, 2013.

[9] 謝鋼. 全球導航衛星系統原理-GPS, 格洛納斯和伽利略系統[M]. 北京: 電子工業出版社,2013:256-259.

[10] 武文俊, 李志剛, 楊旭海,等. 衛星雙向時間頻率傳遞中的Sagnac效應[J]. 宇航學報, 2012, 33(7):936-941. [WuWen-jun,LiZhi-gang,YangXu-hai,etal.Sagnaceffectontwo-waysatellitetimeandfrequencytransfer[J].JournalofAstronautics, 2012, 33(7):936-941.]

[11] 劉麗麗, 王躍科, 陳建云, 等. 導航星座自主時間基準的相對論效應[J]. 宇航學報, 2015,36(4): 470-476. [LiuLi-li,WangYue-ke,ChenJian-yun,etal.Effectsofrelativityinautonomoustimereferencefornavigationconstellation[J].JournalofAstronautics, 2015,36(4): 470-476.]

[12]WeissM,AshbyN.Globalpositioningsystemreceiversandrelativity[J].NISTtechnicalnote, 1999 (1385): 1-46.

[13] 李慶揚. 數值分析(第五版)[M]. 北京：清華大學出版社, 2008:23-26.

[14]ZhouSS,HuXG,LiuL,etal.Applicationsoftwo-waysatellitetimeandfrequencytransferintheBeiDounavigationsatellitesystem[J].ScienceChinaPhysics,Mechanics&Astronomy, 2016, 59(10): 78-86.

[15]HauschildA,MontenbruckO,SteigenbergerP.Short-termanalysisofGNSSclocks[J].GPSsolutions, 2013, 17(3): 295-307.

通信地址：陜西省西安市臨潼區書院東路3號(710600)

E-mail:lvhongchun123@163.com

A Method of Two-Way Satellite-Ground Time Synchronization Under Inter-Satellite Links System

LV Hong-chun1.2,3, LU Xiao-chun1,3,4, WU Jian-feng1,3,5

(1. National Time Service Center, Chinese Academy of Sciences, Xi’ an 710600, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. Key Laboratory of Precision Navigation and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China; 4. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 101408, China; 5. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101408, China)

The mathematical model of the two-way satellite-ground time synchronization is deduced, the method of the two-way satellite-ground time synchronization under inter-satellite links system is proposed, and the relative satellite-ground clock offset of the new-generation BeiDou navigation satellite and the Xi’an station during the orbit test is calculated. The parameters are fitted by the time length of 1 week, 1 day and 1 hour, respectively, and the short-term frequency stability analysis is performed, which verifies the accuracy and performance of the two-way satellite-ground time synchronization of inter-satellite links mode in the experimental stage, and the limited data shows that under the fitting time of 1 week, 1 day and 1 hour, the accuracy of the two-way satellite-ground time synchronization of inter-satellite links mode are up to 3.42 ns, 0.30 ns and 0.15 ns, respectively. And the 10000 s frequency stability is better than 8×10-14.

Inter-satellite links (ISL); Satellite-ground time synchronization; Time-division; BeiDou navigation satellite system (BDS)

2017-03-20;

2017-05-09

P228.4

A

1000-1328(2017)07-0728-07

10.3873/j.issn.1000-1328.2017.07.000

呂宏春(1986-)，男，博士生，主要從事衛星導航定位方法與技術的研究。