以特征值關聯項改進貝葉斯分類器正確率

蔡永泉 王玉棟

(北京工業大學計算機學院 北京 100124)

?

以特征值關聯項改進貝葉斯分類器正確率

蔡永泉 王玉棟

(北京工業大學計算機學院 北京 100124)

樸素貝葉斯分類器建立在其數據“特征值之間相互條件獨立”的基礎上，而在實際應用中該假設難以完全成立。針對這種現象提出一種算法，即通過尋找對產生錯誤分類影響最大的特征值，并依此特征值的關聯項對數據項擴充，在此基礎上對擴充項添加權重，以達到提升分類器精度的效果。最后對權重的大小加以論證，實驗分析了不同大小的權重對分類器正確率的影響。實驗結果表明，添加關聯項擴充訓練集，可以有效提升貝葉斯分類器的正確率。

樸素貝葉斯分類器 貝葉斯算法 貝葉斯分類器

0 引 言

樸素貝葉斯算法是一種在已知先驗概率與類條件概率的情況下的模式分類方法，待分類樣本的分類結果取決于各類域中樣本的全體[1]。樸素貝葉斯分類器(NBC)以貝葉斯公式為基礎，從理論上講精確度高，運算速度快[2]，但也存在以下問題：(1) 在樣本的特征提取不夠優秀時，或對于易出現干擾項的樣本，容易導致分類正確率低。(2) 樣本中有部分數據特征稀疏，會極大地降低NBC分類結果的正確率。因此NBC一般情況下的分類效果難以達到理論高度。

1993年Agrawal等率先提出關聯規則挖掘[3]，它可以對特征值之間的關系進行分析[4]。目前對關聯特征值的關聯項的研究主要是挖掘頻繁集，采集的方法有多種，如Apriori、FP-tree、LPMiner。張陽等[5]曾提出一種類似Apriori算法的冗余剔除算法和特征值篩選方法，使關聯特征值具有更好的分類能力。

本文在NBC的基礎上，在經過一次訓練后，通過訓練結果篩選容易致誤的特征值，并對所有錯誤分類的所包含的特征值進行提取，從中發掘關聯項，對原訓練過程中的樣本集進行提擴充。以0-1分類(兩類分類)為例，根據0和1兩類的先驗條件概率，考慮從樣本集中提取最有可能產生錯誤結果的特征值，并依該特征值尋找關聯點擴充原數據集，從而提高NBC的分類效果。

1 樸素貝葉斯算法

樸素貝葉斯分類方法(NB)是Maron等在1960年提出的一種基于貝葉斯定理的分類算法[6]。其“樸素”在于假設特征值之間條件獨立且位置獨立，即不同特征值之間不存在依賴關系且位置不存在依賴關系。

設T={t1,t2,…,tn}為一個未知分類的n維樣本集合，C={C1,C2,…,Cm}為類別集合，貝葉斯分類算法的目標是將任意的樣本ti分配到類別Ci則可以將貝葉斯分類算法闡述為：任取元組X，將在先驗概率的基礎上把X分類到后驗概率最高的類[7-8]，即NB預測X屬于類別Ci，當且僅當：

P(Ci|X)>P(Cj|X) 1≤j≤mi≠j

(1)

由貝葉斯定理知：

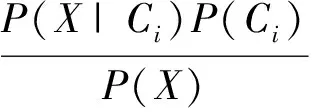
(2)

其中P(Ci|X)為事件Ci在X的情況下發生的概率，P(X|Ci)為先驗條件概率，P(Ci)為先驗類別概率。

對于事件Ci∈C和任意X則有：

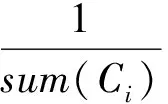
(3)

其中sum(Ci)是類別Ci在總體樣本中的數量，即無論哪個分類Ci下，X發生的概率P(X)都是相同的，因此貝葉斯公式在分類算法中可以近似地簡化為：

P(Ci|X)=P(X|Ci)P(Ci)

(4)

而求解的過程便簡化為求解P(X|Ci)和P(Ci)，其中的關鍵是計算先驗條件概率P(X|Ci)。

雖然實際生活中鑒于特征值的復雜性，特別是在類別C非常復雜的情況下，計算條件概率P(X|Ci)非常困難，然而NB算法假設了元組X中的特征值相互獨立，因此從該假設的基礎上可以得出：

(5)

設函數c為一個函數，則貝葉斯分類器的目標為：

(6)

其中c(X)為滿足argmax函數的條件，使得上式達到最大值。

2 問題分析

NB算法在實際中會遇到如下的問題，設想一個兩類分類(以下簡述為0-1分類)中，存在著0和1兩類數據，當其中的一類中(假設為0類)頻繁出現的某個特征值xi∈X，會有較高的條件概率P(xi|C=0)，而由此現象會有可能產生錯誤分類，但是這種錯誤分類產生有一定的特定條件，同樣以0-1分類為例：

(1) 某個特征值在其中一類出現非常頻繁，而在另一類中出現的幾率較低。

(2) 誤分類項本身較為稀疏。

根據式(6)可知最終分類結果取決于每P(xj|Ci)，因此當條件(1)發生時，會導致c(X)的選擇出現一定的偏差。由于在NB算法中假設了相互獨立，每個屬性對總體概率的影響權重是相同的，即使發生條件(1)并不一定會導致誤分類。

在數據預處理以及特征值提取較好的情況下，NB算法的分類效果較好。但是較好的特征值提取僅僅代表著特征值能較好地表征數據的分類歸屬，仍然不能避免上述兩個條件的情況產生。在數據本身較為稀疏的情況下，甚至會因為個別特殊的特征值而直接產生錯誤分類。下面將從上述條件的角度出發試圖分析并解決該問題。

3 尋找關聯項

在機器學習的過程中常常采用交叉驗證的方式，所謂交叉驗證指的是在訓練樣本較大的情況下，隨機地取訓練樣本的一部分作為測試集。本文在實驗過程中采用了以下方式尋找會產生誤分類的特征值。

3.1 通過結果反饋選擇關聯項

在交叉驗證的過程中，對誤分類項做標記。如果0分類項產生錯誤分類，被標記為1，則標記為錯誤項，反之同理。問題的關鍵是如何判斷在錯誤項中哪些特征值是致誤的。根據第2節中的兩個條件，錯誤分類的關鍵特征值可以從如下步驟進行提取，以0-1分類為例：

(1) 找出錯誤的項，若0類誤分為1，則可以判斷在該項中的特征值中某些或某個在類別為1的條件下的概率過高。

(2) 找出所有P(xi|C=1)>P(xi|C=0)的特征值，作為keys。

(3) 選取一個key與在這些錯誤分類中包含的特征值聯合，并擴充到全體訓練集。

(4) 以擴充后的訓練集重新訓練。

(5) 尋找P(xi=key&xj|C=0)>P(xi=key&xj|C=1)中最大的關聯特征值。

(6) 重復步驟(3)-步驟(5)選出最優的關聯特征值。

(7) 按照以上步驟對把1類誤分為0類的項執行操作，重新訓練并驗證。

給出算法偽代碼(python風格)，該算法用于處理把0類誤分為1類的項。

#val特征值列表，data2train訓練集，data2test測試集，class為分類

def naiveBayes_com(data2train, data2test, class, val):

#p0V為P(xi|C=0) ,p1V為P(xi|C=1),P(C=0)

p0V, p1V, pA = train(data2train, class) # 注釋1

#樸素貝葉斯分類結果dataSet，標記分類正誤

dataSet = naiveBayes(p0V, p1V, pA, data2test)

# 步驟1，dataSet0_1：0類誤分為1類的集合；val0_1：其中包含的特征值

# errorVals為val0_1和val1_0的并集

dataSet0_1, dataSet1_0,val0_1,val1_0, errorVals = sign(dataSet, class)

#p0V0_1是把0類誤分為1的項的P(xi|C=0), p1V0_1同理

p0V0_1, p1V0_1 = getErrorP(p0V, p1V, dataSet)

#步驟2，計算差，提取符合條件的特征值作為備選keys

differP0_1 = p1V0_1 - p0V1_0

index = 0, pIndex = [], pList = []

for(p in differP0_1): #遍歷一條中的每一項

if p>0: #P(xi|C=1)>P(xi|C=0)

pIndex.append(index)

pList.append(p)

index += 1

keysIndex= sorted(pIndex, pList) #注釋3

conL = len(data2train[0]) - 1#data2train的維度

con = -1

conList = []#最終選定的關聯項

for (errorVal in errorVals):#遍歷errorVals

for (key in keysIndex):#遍歷所有的keys

for (data in data2train):#擴充訓練集

if data[errorval] >0 && data[key]>0:

data.append( 1 ) #用關聯項進行擴充

else:

data.append(0)

conR = len(data2train[0]) - 1 #擴充后的維度

#擴充后的訓練結果

p0V_new, p1V_new, pA_new = train(data2train, class)

conIndex = 0 #記錄有效的關聯項

for (con in range(conL, conR)):

if p0V_new[con]>p1V_new:

conIndex = con # 最大的關聯項

conList.append(conIndex)

#命名新的關聯項，并加入到val

return conList, val val.append(newItem(errorval, key))

在樣本維度較大的情況下，上述算法基本不會破壞整體的“相互獨立性”，但是同樣因為其獨立性，按照以上步驟尋找關聯項必然存在著問題，具體實驗結果如表1所示。

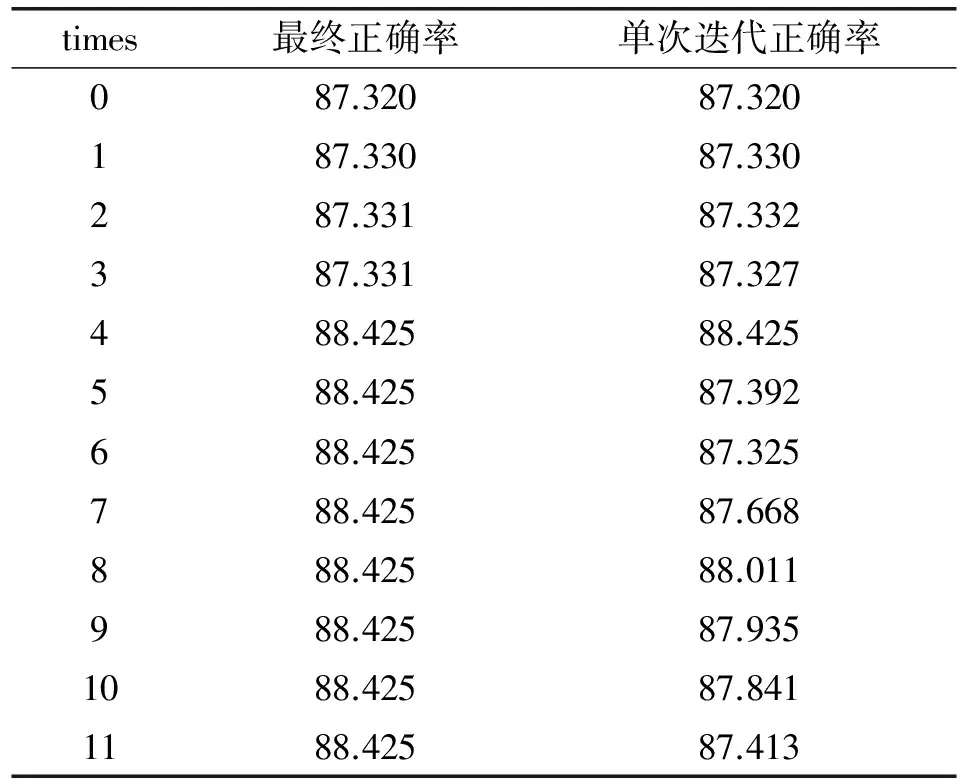
表1 naiveBayes_com算法正確率 %

該實驗只尋找把0類誤分為1類的一組最優的關聯項，單次迭代正確率是實驗過程中為了觀測每次執行步驟(5)的執行效果而加入的觀測量，第0次迭代代表著未進行關聯項選取的正確率。實驗共有11次迭代，每次迭代代表著選取了1組關聯特征值，但不一定是最優的，第11次的迭代結果代表了最終的選擇，可以看到從第4次開始已經找到了最佳的關聯項。但就實驗結果來看，無論是否尋找關聯項，實驗的效果都不好。

3.2 為關聯項設置權重

由式(5)可知P(X|Ci)的值是極小的，若對特征值的提取稍有不恰當會使得出的概率值極低。這在設置權重的時候增加了難度，如果直接使用不僅會造成數據的下溢出，所設置的權重系數可能會極大或者極小。已知f(x)=ln(x)在(0, +∞)的空間上都是單調遞增的，因此在實際操作時對P(X|Ci)取對數是可取的，即：

(7)

(8)

必須強調的是對極小的數據作處理有多種，這里選擇ln函數的目的是因為即便概率低至百萬分之一數量級也可以將權重控制在一個良好的范圍內。再采用了上述算法選取最佳關聯特征值后，將對該關聯特征值訓練后的條件概率添加權重。在設置權重的過程中將權重的范圍設定在一個以0為起點且很大的取值域，逐步縮小兩端點的范圍并計算正確率。采用兩端點的好處是可以觀測權重在一定取值范圍內的效果，避免陷入局部最優點。對權重取兩端進行多次替換和迭代，逐漸縮小范圍計算權重取兩端點時的正確率，并選取正確率最大的點，使得左右端點逼近一個點，如圖1所示。

圖1 左右端點(權重)隨迭代次數的移動

隨著迭代次數的增加，左右端點會逐漸逼近3.732，這是端點在本次實驗的最優解。實際上這是一個求解最優解的過程，存在一個權重w，使得以下兩式同時滿足。

P(C=1|X)>P(C=0|X)C=1

(9)

P(C=0|X)>P(C=1|X)C=0

(10)

在這個過程中參數的選取原則是使得正確率最大，這要求權重的選取盡可能地照顧到0-1兩類分類，即權重為0表示該關聯項不存在，權重過小時關聯項對整體的影響不明顯，反之會將本來正確的一項變成錯誤的。

4 權重選取標準的探討

權重的選擇并不能僅僅把迭代的結果就按照最后的結果，由式(9)和式(10)推測權重w的取值很有可能是一個范圍而不是一個常數，圖2對該推測給出了實驗結果。

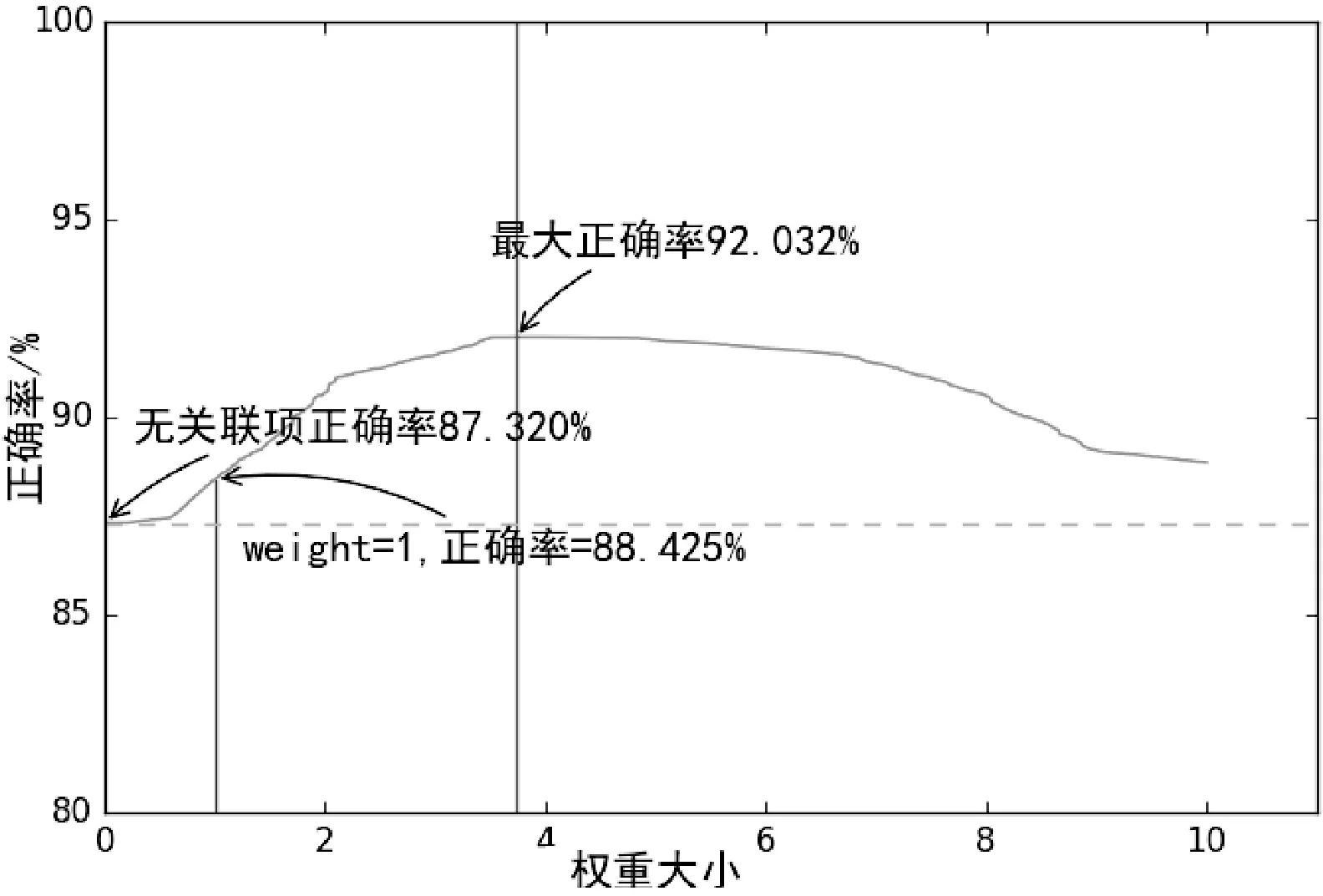
圖2 正確率隨權重改變

在權重接近于0時，關聯項的影響很小，正確率基本沒有變化，隨著權重的增大，在3.732處為92.03%。可以直觀地看到，在頂點處的一片區域內權重的變化對正確率基本沒有影響，由實驗數據得出在(3.506，3.848)之間的正確率都是92.032%，那么上述推測是可以成立的。

4.1 權重的選擇標準

對任何一條數據X其分類標準是求解式(4)，并比較其后驗條件概率P(C=0|X)和P(C=1|X)。在訓練樣本時，上述實驗中所擬合的權重3.732僅從數據上講是最佳的，但是在實際應用中應考慮到盡可能將訓練器擬合到更復雜的情況中來，因此3.732僅僅是一個理想化的取值。為了使得訓練器能適用于更多的樣本，本文將給出評價訓練的一個標準。

對于一條任意的樣本數據X=[x1,x2,…,xn]，定義其概率方差D為：

[(a1+wb1)-(a0+wb0)]2=

(a+bw)2

其中P(C=1|xi)為一條樣本中的一個特征值的概率，a1和a0為對樣本概率取對數后的不設置權重的部分(該部分的權重是1)，可以近似地歸為常數部分，b0和b1為關聯項的概率，這樣便將D近似地轉化為一個關于w的二次函數。

4.2 概率方差的意義

在方差D的式子中，對w求導數，在拐點處D得到一個極小值，反之在一定的取值范圍內，顯然越靠近該取值域的邊緣D的值越大，此時總體上P(C=1|xi)-P(C=0|xi)的絕對值是最大的，使得一條樣本在不同的分類之間的差距最大，那么權重才能更好地擬合復雜樣本。就上述實驗而言，在取值域(3.506，3.848)之間，總是靠近區間兩段的點使得方差D最大，這是權重w的最優的取值。

5 多個關聯項的選取

上述的所有實驗中，只選取了一個關聯項，即是從將0類誤分為1類的樣本中通過改進的NB_C算法中選取了一個關聯項。在多關聯項的選取中，根據NB算法的相互條件獨立的假設，本文總是每次選擇一個關聯項，并對每個關聯項設置最優的權重。這種方法在只用一個關聯項擴充訓練樣本的情況下是最優的，而多關聯項的情況下，由于每個關聯項都設置了權重，在一定程度上拉動了整體的概率，所以正確率并不是最好的。因此本文采用對所有的權重采取批量百分比下降和上升的方法，對每一次下降和上升的步長設定在一定得范圍內，通過比較兩次批量下降和上升后正確率上升的斜率來控制下一次的步幅，其中每次的斜率定義為：

k=(本次的正確率-上次的正確率)/下降步幅

通過這種方法，可以在兩端同時逼近整體最優點時逐漸縮小步伐。

在對權重作批量更新時，應該考慮到保存每一次的最優情況，當遇到最優情況時，應越過最優點，繼續下降或上升，因為整體權重的調整范圍是0至100%之間，因此總能找到一個最優點而不會進入局部最優點。

表2描述了多個selectedCom0_1(從把0類誤分為1類中提取)和selectedCom1_0下使用測試集測試的算法正確率，共選擇合格的selectedCom0_1項11個和selectedCom1_0項6個。在訓練過程中，假設關聯項之間是相互獨立的，然后分別訓練每個關聯項，并賦予權重。最后對所有的權重采取批量百分比下降和上升的方法選擇最優權重。可以明顯看出，隨著關聯項的增多，正確率是單調增加的。這是因為每個關聯項都無法覆蓋所有的樣本，更多的關聯項意味著能更好地覆蓋樣本。

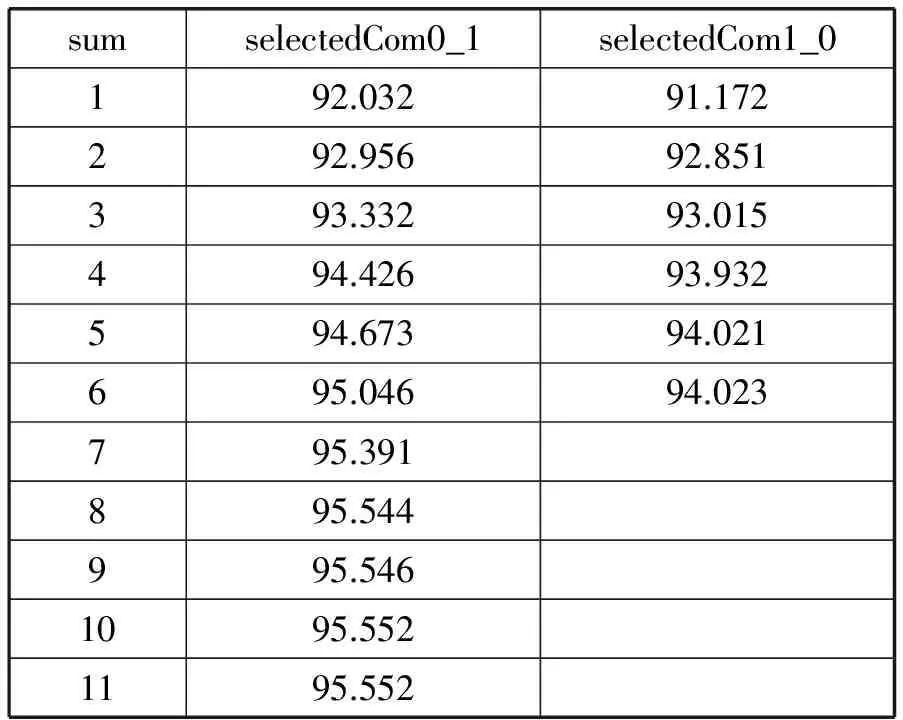
表2 多關聯項下的準確率 %

表3給出了多個關聯項下的正確率。因為本文所用的數據集的維度遠超關聯項的個數，且關聯項大多數覆蓋的是誤差項，所以統計了所能羅列的所有關聯項。可以明確地看出當關聯項增多的時候整體正確率并不是簡單的累加，并在數目達到最大的時候，算法的正確率已經收斂，這說明關聯項之間已經產生了一定的相關性，設置關聯項的數量應該控制在一定的范圍內。

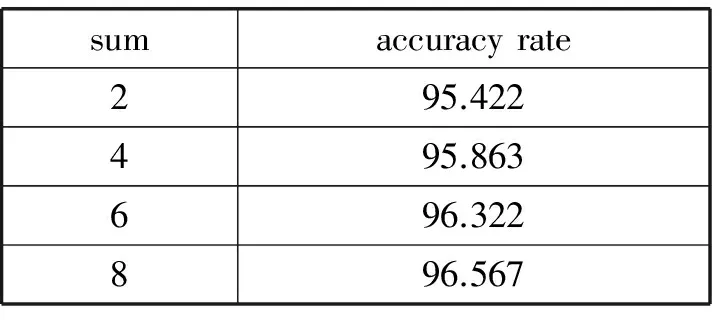
表3 多關聯項下的準確率 %

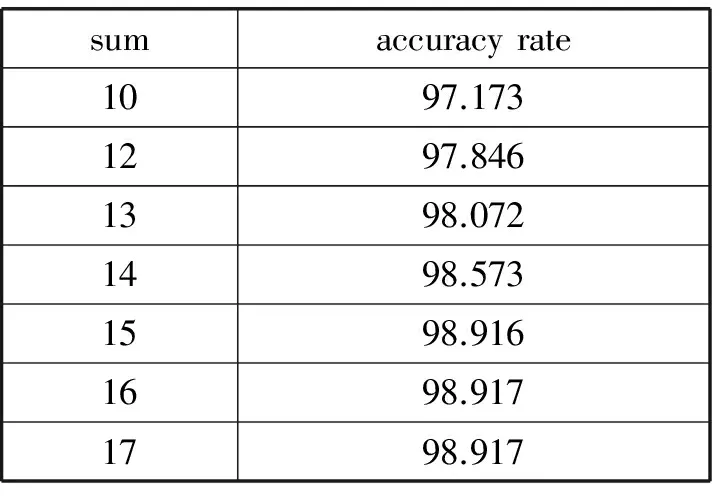
續表3 %

6 結 語

通過一次分類結果從誤分類樣本出發，尋找會產生錯誤的關鍵特征值。根據關鍵特征值選擇關聯項，為關聯項添加權重改善對整體概率的調整能力，并利用方差最大化，使得訓練更加擬合復雜樣本。通過訓練多個關聯項使其更好地覆蓋整體樣本，并且單獨為每個關聯項設置權重，最后批量調整權重。

本文在樸素貝葉斯分類器的基礎上進行研究，對分類器的問題作了分析，以誤分類樣本作為起點，對樸素貝葉斯算法進行改進。加入了一種簡單的尋找關聯項的方法，并對關聯項的權重作了深入探討，提高了樸素貝葉斯算法的分類效果。

[1] 陳凱,朱鈺.機器學習及其相關算法綜述[J].統計與信息論壇,2007,22(5):105-112.

[2] Efron B.Bayes’ theorem in the 21th century[J].Science,2013,340(6137):1177-1178.

[3] Agrawal R,Imieliński T,Swami A.Mining association rules between sets of items in large databases[C]//ACM SIGMOD International Conference on Management of Data.ACM,1999:207-216.

[4] Zhang H,Sheng S.Learning weighted naive Bayes with accurate ranking[C]//IEEE International Conference on Data Mining.IEEE Xplore,2004:567-570.

[5] 張陽,張利軍,閆劍鋒,等.基于關聯特征的樸素貝葉斯文本分類器[J].西北工業大學學報,2004,22(4):413-416.

[6] Maron M E,Kuhns J L.On relevance,probabilistic indexing and information retrieval[J].Journal of the ACM(JACM),1960,7(3):216-244.

[7] 陳新美,潘笑顏,路光輝,等.基于樸素貝葉斯的局部放電診斷模型[J].計算機應用與軟件,2016,33(9):51-55.

[8] 蔣禮青,張明新,鄭金龍,等.基于蝙蝠算法的貝葉斯分類器優化研究[J].計算機應用與軟件,2016,33(9):259-263.

[9] Zhu J,Chen N,Xing E P.Bayesian inference with posterior regularization and applications to infinite latent SVMs[J].Journal of Machine Learning Research,2014,15:1799-1847.

IMPROVENA?VEBAYESCLASSIFICATIONWITHRELATEDITEMS

Cai Yongquan Wang Yudong
(CollegeofComputerScience,BeijingUniversityofTechnology,Beijing100124,China)

Naive Bayes classifier is based on the hypothesis that parameters of the sample are mutually conditional independent. The practical application of this hypothesis is hard to established, so this paper proposes a new algorithm to improve Naive Bayes classifier through looking for properties that have the maximum influence on error classification with an effectively way, finding related items to extend the original data set, then adding weights to the related items. This paper shows the results by experiments, and related items make the classifier work better.

Na?ve Bayes classification Bayes algorithm Bayes classifier

2016-10-15。蔡永泉，教授，主研領域：信息安全。王玉棟，碩士生。

TP3

A

10.3969/j.issn.1000-386x.2017.08.051