大跨度鋼屋蓋組合結構協同工作動力性能研究

劉登明, 肖亞明, 朱飛飛

(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)

?

大跨度鋼屋蓋組合結構協同工作動力性能研究

劉登明, 肖亞明, 朱飛飛

(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)

文章以某大跨度鋼屋蓋-混凝土組合結構為研究對象,利用有限元分析軟件MIDAS/Gen對下部支承結構的3種簡化模型(鉸接支座、彈性支座、考慮下部支承結構質量及剛度的支座)進行分析,得出桁架上、下弦桿的軸力及節點豎向位移隨跨度的變化情況并與整體模型進行對比;對整體結構采用振型分解反應譜法研究不同阻尼比對整體結構抗震性能的影響。結果表明,下部支承結構的不同簡化對桁架結構動力響應影響很大,不可簡單地把下部支承簡化為鉸接支座與彈性支座,否則設計偏于不安全;結構材料阻尼不同,不能簡單地取用某一種材料的阻尼比作為整體結構的阻尼比,確定合適的結構阻尼比,可以進一步提高整體分析的準確性。

慣性效應;協同工作;動力特性;阻尼比;下部支承結構

隨著經濟的發展以及人們對于物質文化生活更高的追求,大跨度場館、展廳等工程項目越來越多,此類工程一般在上部采用大跨度鋼結構屋蓋,下部采用鋼筋混凝土結構。由于結構設計分工的緣故,常把上部結構與下部支承體系分開考慮, 用固定鉸支座模擬上部結構的支承,顯然這樣簡化是不妥的,由此造成的結果將是結構安全上的可靠性降低或者經濟上的巨大浪費[1]。近年有些研究和設計中采用了彈性支座來分析上部結構,能否代替整體分析需要進一步論證[2-3]。本文以某大跨度鋼屋蓋-混凝土組合結構為例,利用MIDAS/Gen結構有限元分析軟件對該工程的整體模型與單獨模型分別進行模態分析以及抗震性能分析,并對結果進行對比,結果表明在引入彈性支座及下部支承結構的質量時,能夠正確地反映下部結構的側向剛度及慣性作用。

1 工程實例分析模型

該工程上部結構采用鋼管桁架體系,下部支承結構采用現澆鋼筋混凝土框架結構,支承點支承在直徑1.0 m的圓柱上。上部結構平面為多邊形,平面尺寸為53.5 m×115.2 m,實際最大跨度50.0 m,高約為19.2 m,采用縱橫向正交正放主次桁架體系,主次桁架系統包括縱向托桁架、橫向主桁架、縱橫向次桁架及封邊環桁架。縱向托桁架和橫向主桁架采用倒三角立體桁架,縱向托桁架高度為3.0 m,橫向主桁架跨中矢高為3.0 m,兩端矢高分別為2.5、2.0 m;縱橫向次桁架及封邊環桁架采用平面桁架,桁架矢高分別為3.0、2.0 m;桁架布置依托屋蓋四周現有混凝土柱定位,同時在開敞端增加2根鋼管搖擺柱。

采用MIDAS/Gen有限元軟件建立的模型如圖1所示。具體模型如下:

模型1 下部支承結構簡化為鉸接支座。

模型2 下部支承結構簡化為彈性支座。

模型3 下部支承結構簡化為彈性支座,同時考慮下部支承結構附加質量。

模型4 整體模型。

建模時鋼筋混凝土框架采用梁單元,剪力墻采用墻單元,鋼結構桁架采用桁架單元。

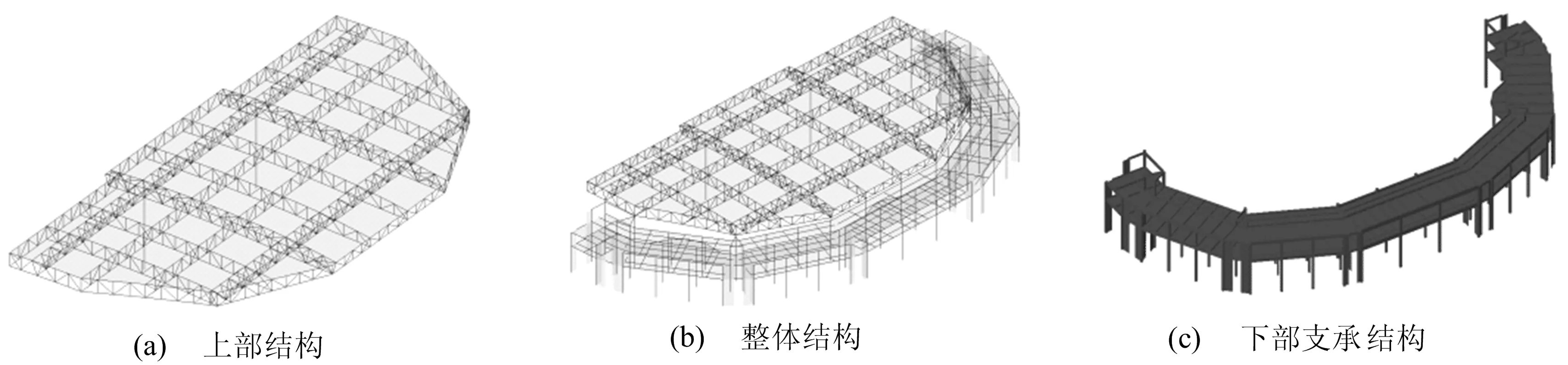
圖1 有限元分析模型

2 耦合體系簡化分析方法

2.1 下部支承結構的彈性效應

考慮下部支承結構在支座約束方向對桁架屋蓋提供的側向剛度,模擬上、下結構協同工作的作用。下部支承結構的彈性效應,可以由下部支承結構在約束方向對桁架屋蓋提供的彈性剛度來表示。彈性剛度的確定方法將依據工程實際情況分別考慮。

(1) 當桁架屋蓋下部支承是剛度較大的結構(如墩體),且桁架屋蓋的自身剛度與其相比很小時,可假定桁架屋蓋支座處為不動鉸支座。當桁架屋蓋下部支承是獨立柱時,豎向位移很小,在支座節點處的豎向約束可以定義為固定約束,其他2個方向的彈性剛度即為柱的抗側剛度,計算公式為:

其中,E為支承柱材料彈性模量;Ix、Iy分別為支承柱截面在x、y方向的慣性矩;Kzx、Kzy分別為支承柱2個水平方向的彈性抗側剛度;H為支承柱的高。

(2) 當桁架屋蓋下部支承是有邊梁的柱和框架梁時,可認為沿邊界法向的抗側移剛度較小,取沿法向抗側移剛度,沿切向邊界和豎向近似認為固定,即考慮支座有水平方向彈性約束,計算下部結構的側向剛度,作為桁架結構水平方向彈性約束的彈簧剛度[4];當桁架支座支承于非框架梁上時,豎向需要考慮其彈性剛度,沿切向和法向也應考慮其抗側剛度[5]。

實際中,梁的彈性剛度即為梁的抗彎剛度,計算公式為:

其中,E為材料彈性模量;I為截面慣性矩;l為梁的跨度。

2.2 支承結構的慣性效應

對于桁架屋蓋與下部支承結構之間具有的相互慣性作用,實際工程中不應忽視。為了定性地分析下部支承結構的慣性效應,可以將下部支承結構的附加質量分配到支座處,并與彈性效應同時考慮。

將下部支承結構的附加質量按總附加質量平均分配給桁架結構各個彈簧支座節點[6],處理方法雖然是近似的,但下部支承結構對桁架屋蓋的慣性作用在一定程度上能夠體現出來。

根據實際支承情況,考慮桁架結構與下部支承結構協同工作,屋蓋支座分布圖如圖2所示。

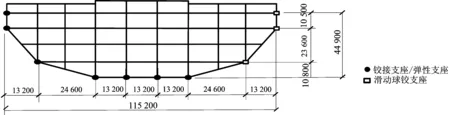
圖2 屋蓋支座分布圖

3 結構的自振特性分析

自振頻率是桁架結構動力特性的一個重要方面,通過對其自振頻率的分析,研究桁架結構不同部分之間剛度是否匹配[7]。利用Block Lanczos法對簡化后的模型及整體結構分別進行模態分析,提取前50階振型,自振頻率結果對比如圖3所示,頻率差值百分比如圖4所示,其中，頻率差值百分比為各簡化模型與整體模型的頻率差值絕對值與整體模型頻率之比。

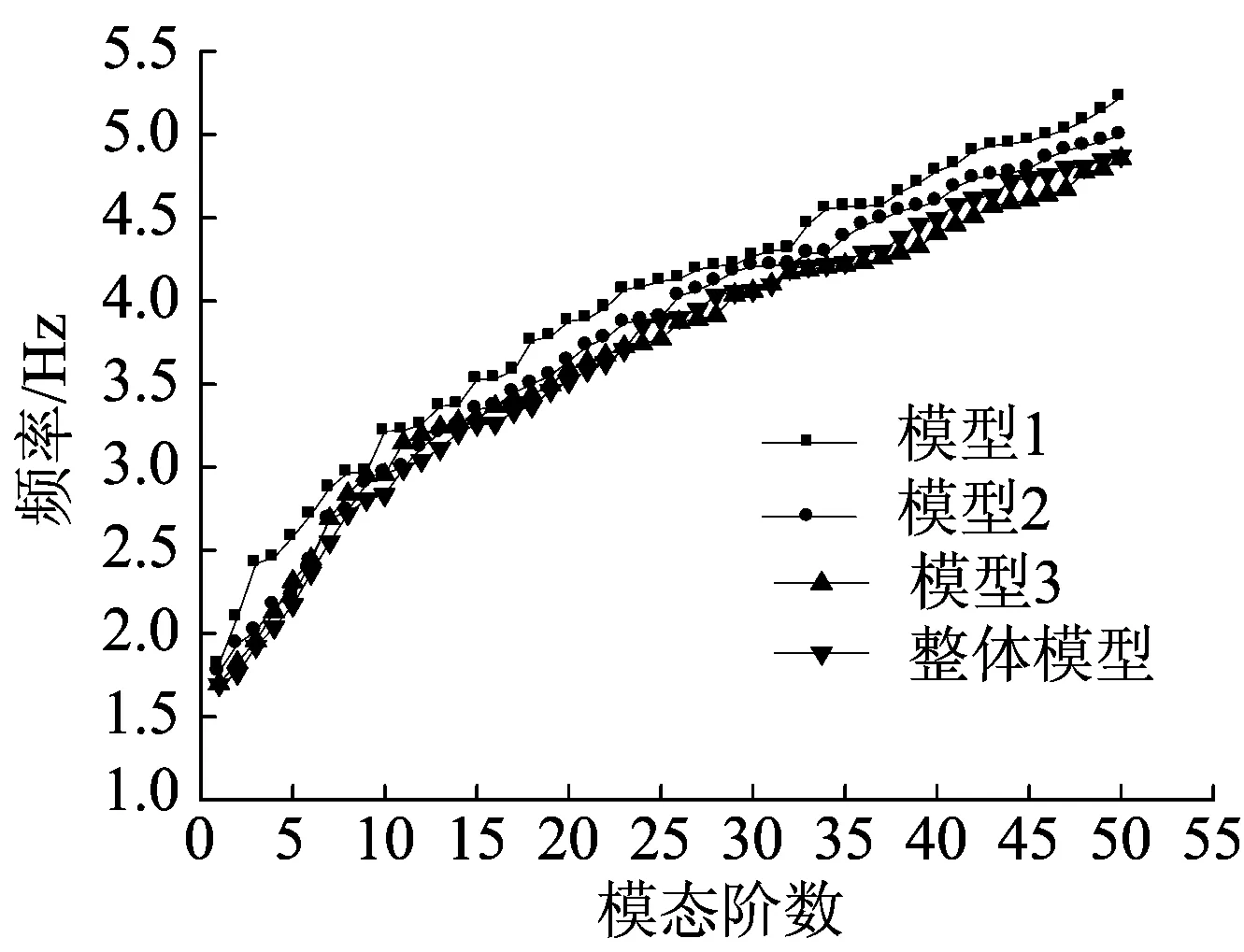
圖3 前50階自振頻率

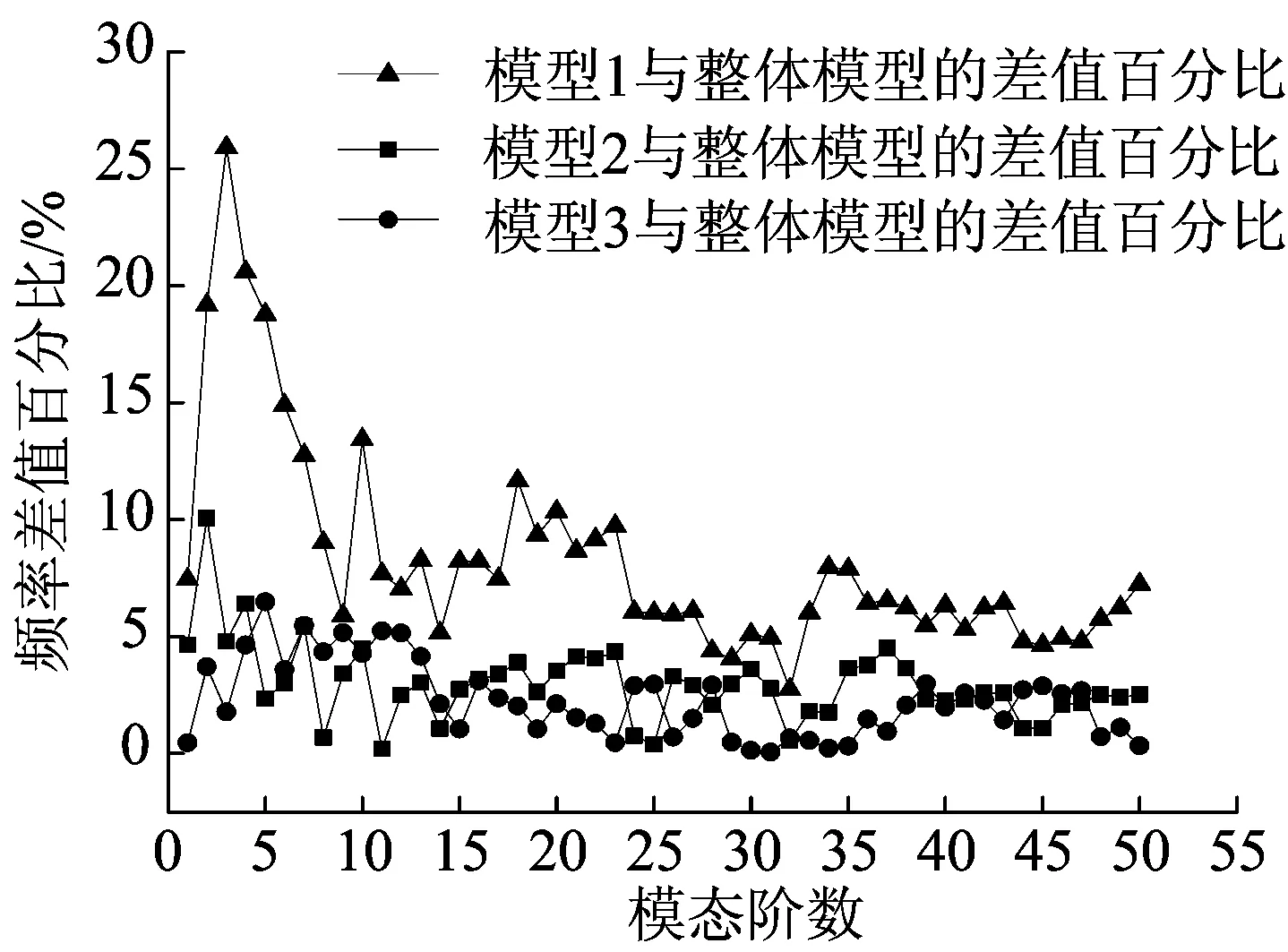
圖4 頻率差值百分比

從圖3可知,不同模型的頻率變化趨勢大體一致,上部桁架結構的基頻較低,主要原因是上部桁架剛度比下部結構剛度小,對于整體模型而言,下部混凝土框架結構剛度很大,前50階頻率基本是屋蓋的振動;同時比較前50階不同模型的振型,發現不同模型下屋蓋的振型形狀一致,頻率變化均勻,未出現頻率跳躍的現象,說明結構動力特性復雜,應考慮多階振型的影響。從圖3還可以看出,模型1的頻率值均大于其他模型,模型3的頻率值與整體模型的頻率值最接近。

從圖4可知,隨著振型階數的增加頻率差值大致呈減小的趨勢。在第3階時,模型1與整體模型頻率差值為26%,達到最大值;在第32階時,模型1與整體模型的頻率差值為3%,達到最小值。在第2階時,模型2與整體模型的頻率差值為10%,達到最大值;在第11階時,模型2與整體模型的頻率差值為0.19%,達到最小值。在第7階時,模型3與整體模型的頻率差值為5.4%,達到最大值;在第30階時,模型3與整體模型的頻率差值為0.06%,達到最小值。前50階自振頻率中,模型3與整體模型的頻率差值在3%占到95%,模型2與整體模型的頻率差值在3% 以內占到65%,模型1與整體模型的頻率差值基本上都大于3%。由此可以看出模型3的自振頻率與整體模型誤差最小。

通過觀察不同模型的前10階振型,可以看出振型可歸納為5類:縱向水平剛體平動振型、跨向水平剛體平動振型、扭轉振型、局部豎向振型及大面積豎向振型。大跨且對稱的空間結構以前2種振型為主,也有不同振型同時出現的耦合振型。

4 結構動力響應及參數分析

根據文獻[8-9],該工程所在地區抗震設防烈度為7度,屬于Ⅲ類場地,地震分組為第1組,場地特征周期值Tg=0.45 s,地震影響系數αmax=0.12;該桁架屋蓋的基頻f=1.7 Hz,相應的周期值T=0.59 s,由于T>Tg,建筑結構地震影響系數曲線出現下降段。本文主要分析雙向地震下桁架屋蓋的動力響應。

4.1 阻尼比的影響

結構阻尼是影響加速度反應譜值的一個重要參數,在結構阻尼比較小的情況下,阻尼比值的變化會大大改變反應譜值,從而影響結構所受地震力的大小。桁架結構的下部支承通常為鋼筋混凝土框架或柱,由于結構材料阻尼不同,不能簡單地取用某一種材料的阻尼比作為整體結構的阻尼比,整體結構為非經典阻尼體系[10]。現行規范[8]針對大跨度鋼屋蓋-混凝土組合結構給出了等效綜合阻尼比取值的參考值范圍,而具體取值尚需計算確定。

本文采用MIDAS/Gen結構有限元分析軟件計算該大跨度鋼屋蓋-混凝土組合結構整體等效綜合阻尼比,采用梁單元、桿單元和桁架單元等不同材料組合結構的ζ計算方法,即位能加權平均法進行計算[11]。計算中采用“組阻尼比”方式輸入,對不同材料的構件進行分組并指定不同的阻尼比,下部鋼筋混凝土ζ1=0.05,上部鋼結構ζ2=0.02。應用概率理論統計方法對結構進行可靠度分析[12],取前200階振型阻尼比,其平均值μz=0.032,標準差σz=0.007,可靠度指標β=4.6,滿足文獻[12]的規定。因此,整體結構等效綜合阻尼比應為0.025～0.039。本文ζ分別取0.020、0.032、0.039、0.050進行分析。選取的主桁架關鍵節點如圖5所示,最大位移對比見表1、表2所列。

在多遇地震作用下,按位能加權平均法計算得到整體模型綜合阻尼比約為0.032,該值在混凝土結構和鋼結構之間。

由表1、表2可知,不同的阻尼比對整體結構的動力響應有明顯影響,節點位移隨著阻尼比的增大將減小;對于這類大跨度鋼屋蓋組合結構而言,地震分析中需考慮下部支承結構協同工作的影響,選取適當的結構綜合阻尼比可以進一步提高整體分析的準確性。

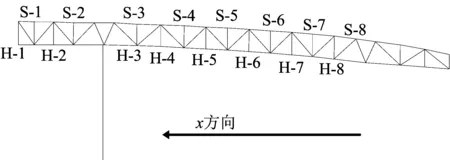
圖5 主桁架關鍵節點

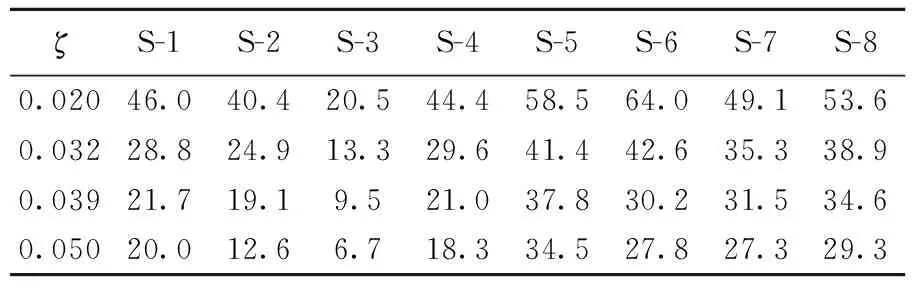
表1 主桁架上弦節點最大位移對比 mm

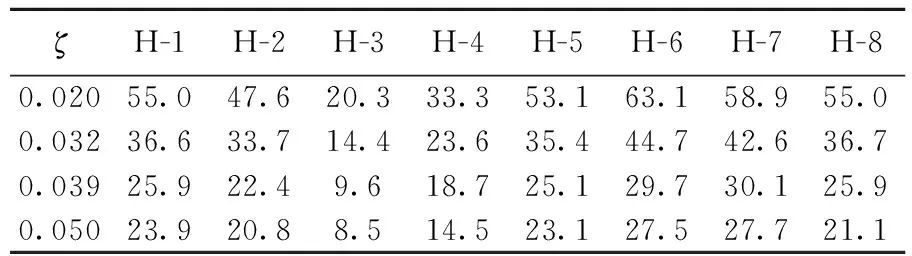
表2 主桁架下弦節點最大位移對比 mm

4.2 簡化模型動力響應分析

為進一步分析上部結構與下部結構協同工作的動力性能,對4種模型分別進行地震響應分析,主桁架上、下弦節點豎向位移計算結果如圖6所示,主桁架上、下弦桿軸力計算結果如圖7所示。在提取整體模型中鋼屋蓋支承點的位移時,發現各個支承點的最大動位移較小,為了簡化設計,將各個支承點的最大動位移簡化為靜力位移分別施加在對應的支承點上,從而在一定程度上減少因不同支座高度對地震響應所帶來的差異。

由圖6、圖7可知,地震作用下不同模型的桁架上、下弦節點的豎向位移及軸力變化趨勢相似,模型1～模型3的計算結果均小于整體模型,但模型3與整體模型的曲線變化最接近,與模型1、模型2相比計算精度有顯著提高。

整體模型與模型3的上弦桿最大桿件軸壓力之比為1.2,其中桿件軸力差值百分比在15%以內占到85%;下弦桿最大桿件軸壓力之比為1.3,其中桿件軸力差值百分比在15%以內占到83%;上弦節點最大節點豎向位移之比為1.1,其中上弦節點豎向位移差值百分比在12%以內占85%;下弦節點最大豎向位移之比為1.2,其中下弦節點豎向位移差值百分比在15%以內占到85%。但是模型3的計算結果仍然偏小,可能得出偏于不安全的結果。

因此實際使用中,對于模型3的計算結果應乘以系數1.3進行適當的修正。

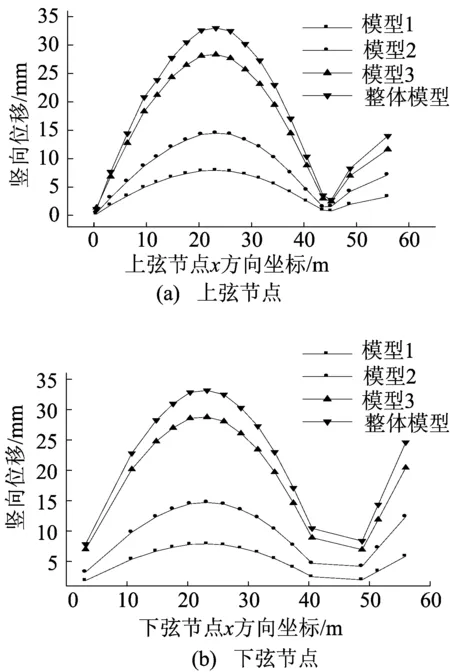
圖6 不同簡化模型下主桁架上、下弦節點豎向位移

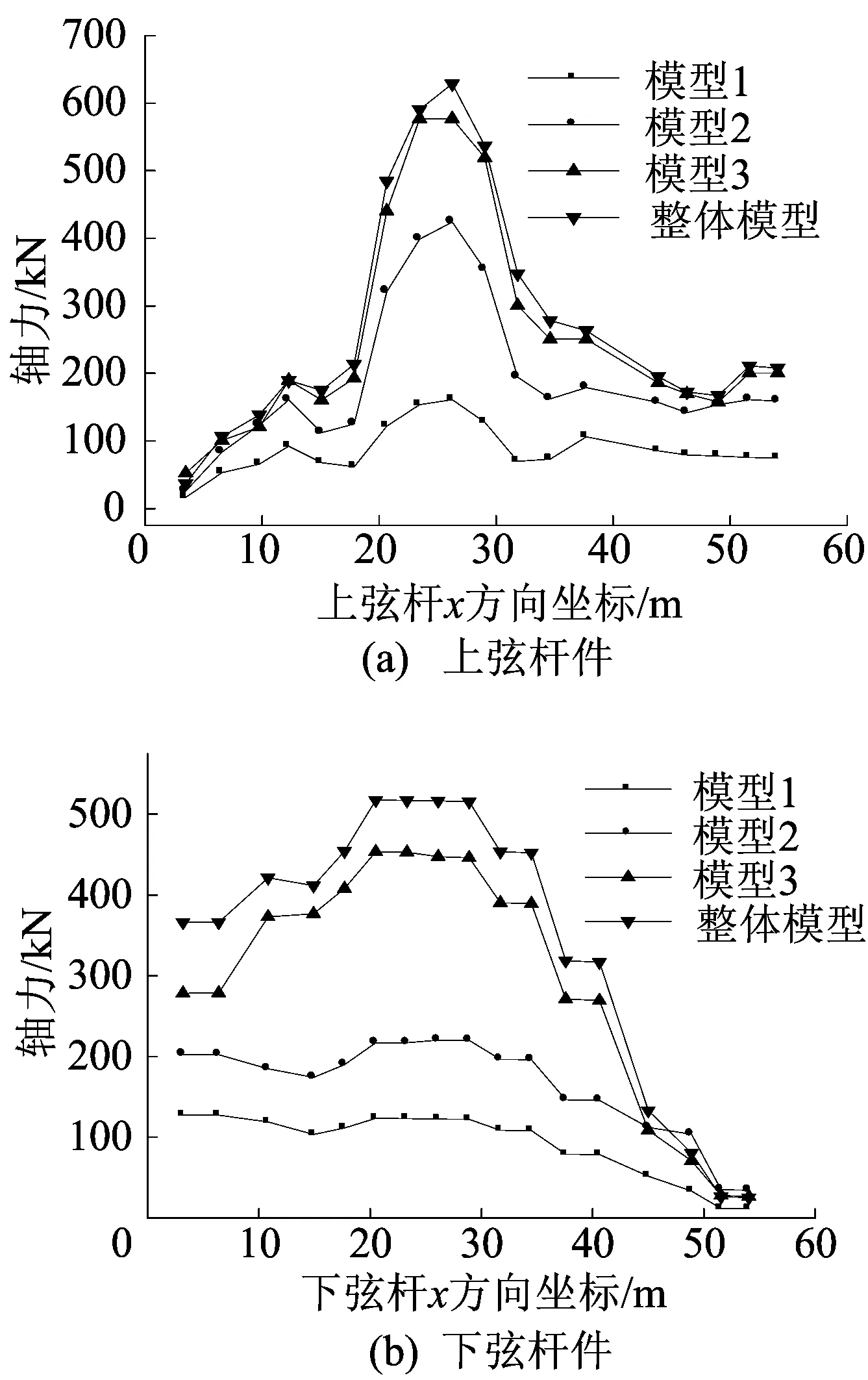
圖7 主桁架上、下弦桿軸力

5 結 論

(1) 模型1與整體模型的頻率差值最大為26%,模型3與整體模型的頻率差值總體上在3%以內,若采用下部支承結構簡化模型1、模型2代替整體模型進行地震反應分析,結構的動力特性將會極大地改變,從而改變地震力的大小及分布。

(2) 對于大跨度鋼屋蓋-混凝土組合結構,取單一阻尼比進行抗震計算會使結構節點豎向位移與實際不符,建議采用應變能阻尼比法進行抗震設計以提高整體分析的準確性。

(3) 對下部支承結構簡化時應考慮其彈性剛度及慣性作用,計算結果應乘以系數1.3進行適當地修正。

[1] 沈祖炎,嚴慧,馬克儉,等.空間網架結構[M].貴陽:貴州人民出版社,1987:30-55.

[2] 魏強,倪先光,齊政.大跨度體育館鋼-混凝土混合結構設計與分析[J].建筑結構,2014,44(15):29-35.

[3] 王秀麗,王磊,薛素鐸.大跨度復雜屋面組合結構協同工作動力性能研究[J].北京工業大學學報,2010,36(9):1215-1221.

[4] 陳應波,陳軍明.網殼結構與下部結構協同工作的研究[J].華中科技大學學報(自然科學版),2004,32(3):49-53.

[5] 邵力群,黃振民,余志祥.目前網架支座及支承框架設計存在的幾個問題[J].四川建筑工程結構,2009,29(3):98-101.

[6] 支旭東,于志偉,范峰.下部支承結構對網殼結構強震響應的影響研究[J].建筑鋼結構進展,2012,14(4):27-31.

[7] 藍天,張毅剛.大跨度屋蓋結構抗震設計[M].北京:中國建筑工業出版社,2000:25-35.

[8] 中華人民共和國住房和城鄉建設部.建筑抗震設計規范:GB 50011—2010[S].北京:中國建筑工業出版社,2010: 171-192.

[9] 郭繼武.建筑抗震設計[M].北京:中國建筑工業出版社,2011:52-71.

[10] 俞欣,陽光.鋼-混凝土混合結構阻尼分析方法[J].建筑結構,2013,43(增刊2):467-471.

[11] 曹資,張超,張毅剛,等.網殼屋蓋與下部支承結構動力相互作用研究[J].空間結構,2001,7(2):19-26.

[12] 中華人民共和國建設部.建筑結構可靠度設計統一標準:GB 50068—2001[S].北京:中國建筑工業出版社,2001:8-10.

(責任編輯 張淑艷)

Research on dynamic performance of large-span steel roof composite structure with cooperative working behavior

LIU Dengming, XIAO Yaming, ZHU Feifei

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

Taking a large-span steel roof-concrete composite structure as study object, three simplified models of the lower supporting structure including hinge support, elastic support, support considering the quality and rigidity of the lower supporting structure are analyzed by using the finite element analysis software MIDAS/Gen. The change of the axial force of upper and lower chords of the truss and the vertical displacement of nodes with the span is discussed, and the results are compared with those of the overall model. The effect of different damping ratios on the seismic behavior of the overall structure is also studied by using the mode-superposition response spectrum method. The results show that the different simplification of the lower supporting structure has a great influence on the dynamic response of truss structure. The lower bearing cannot simply be simplified as the hinge support and the elastic support, otherwise the design will be unsafe. Due to different damping of the structural materials, the damping ratio of a certain kind of material cannot simply be taken as that of the overall structure. With the determination of the appropriate structural damping ratio, the accuracy of the overall analysis can be further improved.

inertial effect; cooperative work; dynamic characteristic; damping ratio; lower supporting structure

2015-11-27；

2016-03-03

劉登明(1988-),男,安徽淮南人,合肥工業大學碩士生; 肖亞明(1960-),男,安徽合肥人,合肥工業大學副教授,碩士生導師.

10.3969/j.issn.1003-5060.2017.07.019

TU393.3

A

1003-5060(2017)07-0960-05