一類2-重量碼和兩類3-重量碼

李蘭強, 劉 麗

(合肥工業大學 數學學院,安徽 合肥 230009)

?

一類2-重量碼和兩類3-重量碼

李蘭強, 劉 麗

(合肥工業大學 數學學院,安徽 合肥 230009)

設F是含有q個元素的有限域,其中q是一個奇素數p的正整數冪。文章利用F到Fp的跡映射Tr,構造Fp上兩類3-重量線性碼和一類2-重量線性碼,并計算這些線性碼的重量分布;所構造的這三類線性碼可以用于密鑰共享體制的構造。

有限域;線性碼;指數和;重量分布;密鑰共享體制

0 引 言

線性碼是一類非常重要的碼,尤其是少重量線性碼。它們在密鑰共享體制和認證碼方面有廣泛的應用。此外，在消費電子和網絡通信以及數據存儲方面也有應用。因此,尋找有限域上的少重量線性碼是學者們研究的熱點之一。

W(Z)=1+A1Z+A2Z2+…+AnZn,

而(1,A1,A2,…,An)稱為碼C的Hamming重量分布。若(A1,A2,…,An)中不為0的Ai的個數為t,則稱碼C為t-重量碼。

通過某個Gray映射,將環上的線性碼映射為域上線性碼是構造域上線性碼的常見方法[2-4],但用這種方法很難計算出碼的重量分布。

本文是用另一種方法構造有限域上的線性碼。對于任意集合D={d1,d2,…dn}?F,可以構造一個長度為n的線性碼，即

CD={(Tr(d1x),Tr(d2x),…,Tr(dnx)):x∈F},

其中,D被稱為碼CD的定義集。文獻[5-6]用這個方法分別構造了一類3-重量二元線性碼和一類2-重量二元線性碼,這些碼可以用在密鑰共享體制和認證碼等方面。目前,已有不少學者用這個方法構造少重量線性碼[7-10]。本文在上述研究的基礎上構造少重量線性碼,給出相應參數和重量分布。

1 預備知識

F的一個加法特征是從F到非零復數集的非零函數χ,且對任意x,y∈F,有χ(x+y)=χ(x)·χ(y)。對任意b∈F,可定義加法特征為:

?c∈F,

此外F*的乘法特征定義為:

其中,0≤j≤q-2;α為F*的一個生成元。當j=(q-1)/2時,稱ψj為F*的二次特征,記為η。F上的高斯和G(ψ,χ)定義為:

其中,ψ為F*的乘法特征；χ為F的加法特征。當ψ=η,χ=χ1時,補充η(0)=0,則有:

類似地,有Fp上的高斯和為：

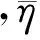
由文獻[11]可得引理1與引理2。

引理1 符號如上所述,則有:

引理2 設χ是F的一個非平凡加法特征,ψ是F的一個乘法特征,且ψ的階為d=gcd(n,q-1),n∈N,則有:

其中,a,b∈F且a≠0。

定理1 設f(x)=ax2t+bxt∈F[x],其中,gcd(q-1,t)=1且a≠0,則有:

由文獻[7]可得如下引理3。

引理4 設p是一個奇素數,q=pm且滿足gcd(t,q-1)=1,則對任意a∈Fp,有

證明 由引理2,可得:

(1) 若a=0,則

(2) 若a≠0,則

證明 由定理1可知:

若Tr(b2)=0,則有:

若Tr(b2)≠0,則有:

定理2 設na=|{x∈F:Tr(x2t)=a}|,其中,a∈Fp,gcd(t,q-1)=1,則有:

再由引理4得:定理2的結論成立。

2 主要結果

本文選取Da={x∈F*:Tr(x2t)=a},其中,a∈Fp;gcd(t,q-1)=1。由該定義集可得:

CDa={(Tr(xtd1),Tr(xtd2),…,Tr(xtdn)):x∈F},

令N(b)=|{x∈F:Tr(x2t)=a,Tr(bxt)=0}|,記碼CDa的碼字cb的Hamming重量為W(cb),則有:

W(cb)=na-N(b)

(1)

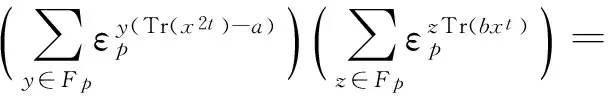
(2)

表1 m為奇數時線性碼CD0的重量分布

表2 m為偶數時線性碼CD0的重量分布

由定理3可知,當a=0時,可以得到Fp上一類3-重量線性碼和一類2-重量線性碼。這2類線性碼已經在文獻[7]中被研究,故本文僅作簡單介紹。本文主要研究a≠0的情況。

W(cb)=na-N(b)=

證明 由引理4、引理5及(2)式得:

ω1=pm-1-pm-2,

則由定理2可得:

Aω1=pm-1-1,

當a是模p的二次非剩余時,同理可證。

表3 a是模p二次剩余時線性碼CDa的重量分布

表4 a是模p二次非剩余時線性碼碼CDa的重量分布

例1 設a=1,p=5,m=3,則碼CD1是一個參數為[30,3,20]的線性碼,且其重量計數器為1+24Z20+60Z24+40Z26。

例2 設a=2,p=3,m=5,則碼CD2是一個參數為[90,5,54]的線性碼,且其重量計數器為1+80Z54+90Z60+72Z66。

證明 與定理4的證明類似。

表5 m為偶數線性碼CDa的重量分布

例3 設a=1,p=3,m=4,則碼CD1是一個參數為[30,4,18]的線性碼,且其重量計數器為1+50Z18+30Z24。

例4 設a=2,p=5,m=2,則有線性碼CD2,其參數為[6,2,4]且重量計數器為1+12Z4+12Z6。已知參數為[6,2]的線性碼的極小距離d最大可以是5,因此碼[6,2,4]是一個幾乎最優碼。

因此,本文構造的兩類3-重量線性碼和一類2-重量線性碼均可用于密鑰共享體制的構造。

3 結 論

本文取定義集Da={x∈F*:Tr(x2t)=a},其中a∈Fp,gcd(t,q-1)=1;再利用F到Fp的跡映射Tr構造Fp上的線性碼。當a=0時,所得到的線性碼與文獻[7]中定理1與定理2所述的線性碼一樣。本文主要研究a≠0的情況,得到了Fp上兩類3-重量線性碼和一類2-重量線性碼,并給出其重量分布。此外,在一定條件下,本文構造的兩類3-重量線性碼和一類2-重量線性碼均可用于密鑰共享體制的構造。

[1] HUFFMAN W C,PLESS V.Fundamentals of error-correcting codes [M].New York:Cambridge University Press,2003:1-15.

[2] 朱士信,吳波.環Fp+uFp+…+ukFp上的線性碼和常循環碼的Gray像[J].合肥工業大學學報(自然科學版),2006,29(8):1049-1052.

[3] 張付麗,開曉山,陳安順.環F2m+uF2m上常循環碼及其Gray像[J].合肥工業大學學報(自然科學版),2015,38(1):136-139.

[4] 徐露露,劉麗.環R上的一類常循環碼及自對偶碼[J].合肥工業大學學報(自然科學版),2014,37(2):253-256.

[5] DING K,DING C.Binary linear codes with three weights[J].IEEE Commun Lett,2014,18(11):1879-1882.[6] WANG Q,DING K,XUE R.Binary linear codes with two weights[J].IEEE Commun Lett,2015,19(7):1097-1100.

[7] DING K,DING C.A class of two-weight and three-weight codes and their applications in secret sharing[J].IEEE Trans.Inform.Theory,2015,61(11):5835-5842.

[8] DING C,NIEDERREITER H.Cyclotomic linear codes of order 3[J].IEEE Trans Inform Theory,2007,53(6):2274-2277.

[9] ZHOU Z,DING C.A class of three-weight cyclic codes[J].Finite Fields and Their Appl,2014,25:79-93.

[10] DING C,GAO Y,ZHOU Z.Five families of three-weight ternary cyclic codes and their duals[J].IEEE Trans.Inform Theory,2013,59(12):7940-7946.

[11] LIDL R,NIEDERREITER H.Finite field[M].New York:Cambridge University Press,1997:186-226.

[12] YUAN J,DING C.Secret sharing schemes from three classes of linear codes[J].IEEE Trans Inf Theory,2006,52(1):206-212.

(責任編輯 朱曉臨)

A class of two-weight and two classes of three-weight codes

LI Lanqiang, LIU Li

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

LetFbe a finite field withqelements, whereqis a positive power of an odd primep. In this paper, there are two classes of three-weight and a class of two-weight linear codes overFpconstructed by using the trace function Tr fromFtoFp. The weight distributions of these classes of linear codes are also determined. In addition, these classes of linear codes can be used in secret sharing schemes.

finite field; linear code; exponential sum; weight distribution; secret sharing scheme

2016-04-13

國家自然科學基金資助項目(11401154);安徽省省級質量工程專業綜合改革試點資助項目(2012zy007)和名師(大師)工作室資助項目(2015msgzs126)

李蘭強(1991-),男,安徽蒙城人,合肥工業大學碩士生; 劉 麗(1965-),女,安徽安慶人,博士,合肥工業大學教授,碩士生導師.

10.3969/j.issn.1003-5060.2017.07.027

TN911.22

A

1003-5060(2017)07-1004-05