透射邊界條件在波動(dòng)譜元模擬中的實(shí)現(xiàn):二維波動(dòng)1)
邢浩潔 李鴻晶
(南京工業(yè)大學(xué)土木工程學(xué)院,南京211816)
固體力學(xué)
透射邊界條件在波動(dòng)譜元模擬中的實(shí)現(xiàn):二維波動(dòng)1)
邢浩潔 李鴻晶2)
(南京工業(yè)大學(xué)土木工程學(xué)院,南京211816)
將邢浩潔和李鴻晶提出的多次透射公式(multi-transmitting formula,MTF)的譜元格式應(yīng)用于均勻介質(zhì)中線彈性SH波動(dòng)問(wèn)題的譜元模擬.假定緊鄰人工邊界的一層譜單元為具有直線邊界的四邊形單元,以保證每個(gè)人工邊界節(jié)點(diǎn)都唯一對(duì)應(yīng)一條指向內(nèi)域的離散網(wǎng)格線.人工邊界節(jié)點(diǎn)在某時(shí)刻的位移由該離散網(wǎng)格線上的節(jié)點(diǎn)在前若干時(shí)刻的位移確定,按照MTF譜元格式進(jìn)行計(jì)算.通過(guò)平面波以一定角度傳播的外源問(wèn)題算例和點(diǎn)源脈沖自由擴(kuò)散的內(nèi)源問(wèn)題算例,驗(yàn)證了方法的可行性以及對(duì)實(shí)際復(fù)雜波動(dòng)問(wèn)題的適用性.通過(guò)不同類型初值問(wèn)題算例,在時(shí)域內(nèi)分析了插值多項(xiàng)式階次、人工波速和透射階次三個(gè)參數(shù)對(duì)反射誤差的影響.結(jié)果表明:插值多項(xiàng)式階次較高的格式會(huì)表現(xiàn)出更好的精度,但總體上對(duì)反射誤差的影響較小;人工波速對(duì)反射誤差具有顯著影響,當(dāng)人工波速小于介質(zhì)物理波速時(shí)反射誤差較大,而當(dāng)人工波速等于或稍大于介質(zhì)物理波速時(shí)反射誤差處于較低水平;透射階次對(duì)反射誤差具有決定性影響,表現(xiàn)在不失穩(wěn)的情形下提高透射階次能夠迅速降低反射誤差,但內(nèi)源問(wèn)題從三階MTF開(kāi)始出現(xiàn)飄移失穩(wěn),外源問(wèn)題從二階MTF開(kāi)始出現(xiàn)輕微的飄移失穩(wěn).
多次透射公式,譜元法,SH波動(dòng),MTF譜元格式,飄移失穩(wěn)
引言
局部場(chǎng)地的地震波動(dòng)數(shù)值模擬是地震學(xué)和地震工程等領(lǐng)域的重要課題,這類復(fù)雜介質(zhì)中的大規(guī)模開(kāi)放系統(tǒng)問(wèn)題,對(duì)計(jì)算模型的空間離散以及人工邊界條件都有很高要求.譜元法[2](spectral element method,SEM)兼具了有限元法的靈活性和譜方法的高精度,具有高效處理復(fù)雜幾何或物理模型的能力,成為近年來(lái)備受關(guān)注的空間離散方法.從20世紀(jì)90年代開(kāi)始,譜元法被用于求解地震波傳播問(wèn)題,在地球介質(zhì)中的聲波和彈性波模擬方面取得了進(jìn)展[310].近十年來(lái)對(duì)譜元法的研究逐漸增多,在譜元法基本理論[11]、大規(guī)模地震動(dòng)模擬[1214]、三角網(wǎng)格劃分[1518]、并行計(jì)算[19]、非線性分析[20]以及與有限元法的對(duì)比[21]等方面都有成果發(fā)表.可以說(shuō),在處理大規(guī)模復(fù)雜波動(dòng)問(wèn)題方面,譜元法比傳統(tǒng)有限差分法[22]或有限元法[23]具有顯著優(yōu)勢(shì).但由于譜元法在有限單元上采用了基于不等距節(jié)點(diǎn)的高階插值格式,傳統(tǒng)的以有限元法等采用低階插值格式構(gòu)造的人工邊界條件計(jì)算公式在波動(dòng)譜元模型中無(wú)法被直接使用,因此需要專門研究適合譜元模型的人工邊界條件的具體實(shí)現(xiàn)方式.
Clayton-Engquist(CE)邊界[24]是早期在譜元法地震波動(dòng)模擬中使用最多的人工邊界條件,它與譜元法結(jié)合的方式有兩種,一種需將邊界表達(dá)式寫(xiě)成沿邊界的等效積分并納入到譜元法的等效積分方程中[4],另一種則將邊界表達(dá)式寫(xiě)成關(guān)于邊界上黏性阻尼力以及法向、切向應(yīng)力的形式[79].作為一種時(shí)、空局部化的近似邊界,它僅能吸收傳播方向與邊界法線夾角較小的外行波動(dòng).全局化的DtN邊界在譜元法中有一定應(yīng)用[2527],該邊界由波傳播的遠(yuǎn)場(chǎng)解得到,是一種精確的人工邊界.但全局邊界的計(jì)算量很大,許多實(shí)際波動(dòng)問(wèn)題的遠(yuǎn)場(chǎng)解比較復(fù)雜,而在數(shù)值計(jì)算中需要對(duì)級(jí)數(shù)表達(dá)式進(jìn)行截?cái)郲28],這些都限制了該邊界的推廣.完美匹配層(perfectly matched layer,PML)邊界是目前波動(dòng)譜元模擬中比較熱門的人工邊界[2933],其優(yōu)點(diǎn)在于外行波在內(nèi)域和吸收層的交界面上不發(fā)生反射,而且能夠迅速地被吸收層內(nèi)的衰減函數(shù)和阻尼作用消減掉.但無(wú)論是經(jīng)典PML,還是復(fù)頻移PML,形式都比較復(fù)雜,而且數(shù)值離散后的PML仍然存在精度和穩(wěn)定性問(wèn)題.最近,多次透射公式(multi-transmitting formula,MTF)[3435]被嘗試引入波動(dòng)譜元模擬中,文獻(xiàn)[36]從時(shí)間回退和空間回退兩個(gè)角度,給出了在譜元法中使用多次透射公式的方法并探討了其穩(wěn)定性問(wèn)題.
MTF通過(guò)透射階次和人工波速兩個(gè)參數(shù)控制透射精度,譜元法則通過(guò)單元階次和單元尺度來(lái)模擬復(fù)雜波場(chǎng),兼具高精度和靈活性是二者的相似之處.因此,在波動(dòng)譜元模擬中使用MTF作為人工邊界條件,可能是提高波動(dòng)模擬精度和計(jì)算效率的重要途徑之一.MTF易于與內(nèi)域離散格式結(jié)合,但關(guān)于這方面的研究不多.目前在波動(dòng)有限差分或有限元模擬中廣泛使用的是一種基于三點(diǎn)拋物線內(nèi)插和齊次內(nèi)插遞推過(guò)程的MTF數(shù)值格式[37].在文獻(xiàn)[1]中,我們?cè)敿?xì)探討了在譜元離散網(wǎng)格中施加MTF時(shí)所面臨的新問(wèn)題,提出了一組基于拉格朗日多項(xiàng)式插值和簡(jiǎn)單內(nèi)插方案的MTF譜元格式,并在一維波動(dòng)問(wèn)題中研究了這組格式的精度和穩(wěn)定性特點(diǎn).本文將根據(jù)文獻(xiàn)[1]提出的MTF譜元格式,進(jìn)一步探討在二維波動(dòng)譜元模擬中實(shí)現(xiàn)MTF的具體方法,分析方法的可行性以及復(fù)雜波動(dòng)問(wèn)題的物理特征與MTF計(jì)算參數(shù)之間的聯(lián)系,并初步探討與之相關(guān)的穩(wěn)定性問(wèn)題.
1 二維波動(dòng)譜元模型
以SH型波動(dòng)問(wèn)題說(shuō)明譜元法的基本公式以及MTF的實(shí)現(xiàn)過(guò)程.SH波動(dòng)方程為如下的二維標(biāo)量波方程
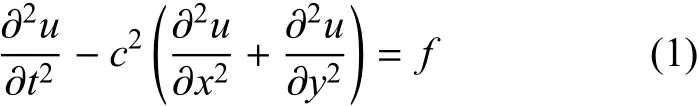
其中,u(x,y,t)為出平面波動(dòng)位移,f(x,y,t)為外荷載,c為介質(zhì)物理波速.模型所在區(qū)域?yàn)?x,y)∈Ω,計(jì)算時(shí)間t∈(0,T].
采用具有集中質(zhì)量矩陣的高精度勒讓德譜元法(Legendre spectralelementmethod,LSEM)對(duì)波動(dòng)方程進(jìn)行空間離散,通過(guò)以下3個(gè)步驟:(1)導(dǎo)出原方程的等效積分“弱”形式;(2)將整個(gè)計(jì)算區(qū)域的積分劃分為各個(gè)單元積分的疊加;(3)將各個(gè)單元的積分和微分轉(zhuǎn)換到標(biāo)準(zhǔn)的參考單元上.得到波動(dòng)方程的等價(jià)形式如下
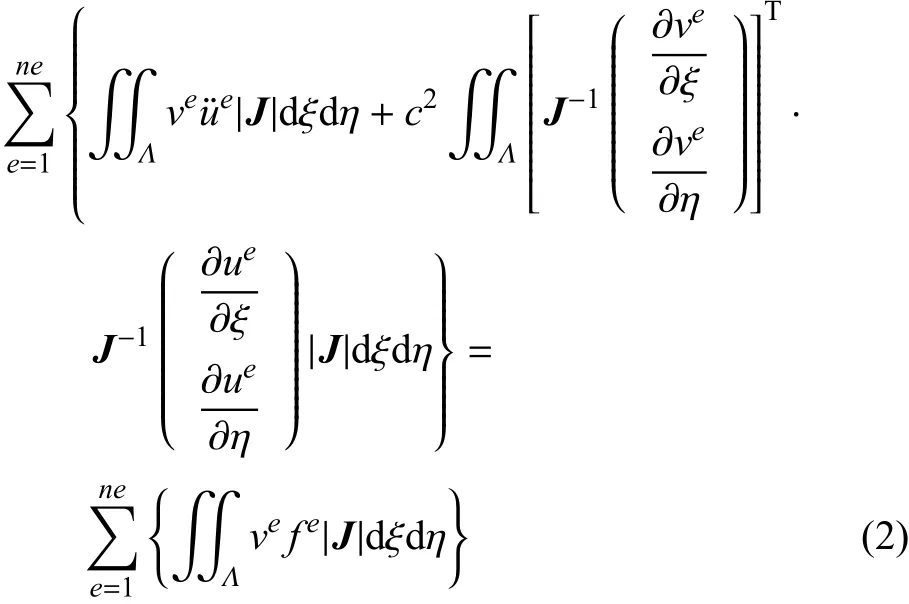
其中,ue(ξ,η),ve(ξ,η)分別為參考單元上的波動(dòng)位移函數(shù)和測(cè)試函數(shù),頂標(biāo)“¨”表示對(duì)時(shí)間的二階偏導(dǎo)數(shù),上標(biāo)T表示向量或矩陣的轉(zhuǎn)置.ne為模型的單元數(shù);Λ為參考單元,ξ,η為參考單元坐標(biāo);|J|和J-1為雅可比行列式以及雅可比矩陣的逆陣.
參考單元上的波動(dòng)位移函數(shù),即LSEM的單元位移模式由下式定義

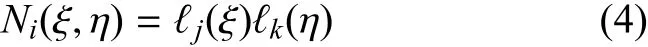
式中,單元的總體節(jié)點(diǎn)編號(hào)i以及ξ,η方向的局部節(jié)點(diǎn)編號(hào)j,k如圖1所示.單元節(jié)點(diǎn)數(shù)ng=nξ×nη,這里nξ,nη分別為ξ,η方向的節(jié)點(diǎn)數(shù).
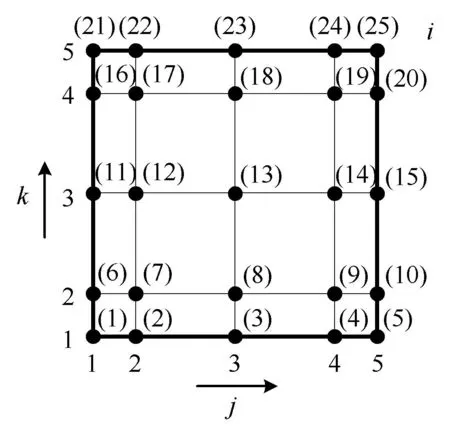
圖1 參考單元的節(jié)點(diǎn)編號(hào)Fig.1 Nodenumbering of a referenceelement
勒讓德基函數(shù)為定義在GLL(Gauss Lobatto Legendre)節(jié)點(diǎn)上的拉格朗日插值函數(shù),具有表達(dá)式
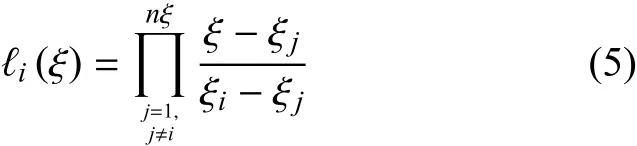
式中,GLL節(jié)點(diǎn)ξi,ξj是數(shù)值分析和工程計(jì)算中的一類重要節(jié)點(diǎn),很多文獻(xiàn)都給出了其數(shù)值,這里不再贅述.η方向的勒讓德基函數(shù)定義與上式相同.
方程(2)再經(jīng)過(guò)如下步驟:利用伽遼金原理,選取與波動(dòng)位移函數(shù)相同的測(cè)試函數(shù);將波動(dòng)位移函數(shù)、測(cè)試函數(shù)、雅可比行列式以及雅可比逆矩陣代入方程(2),根據(jù)二維GLL數(shù)值積分計(jì)算各個(gè)積分項(xiàng),得到各個(gè)單元的運(yùn)動(dòng)方程;將單元方程組裝為總體方程.得到空間離散后的譜元節(jié)點(diǎn)運(yùn)動(dòng)方程
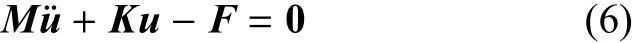
式中,M為總體質(zhì)量矩陣,K為總體剛度矩陣,F(xiàn)為外載荷向量,u為被求的節(jié)點(diǎn)位移.
這個(gè)運(yùn)動(dòng)方程是關(guān)于模型所有內(nèi)域節(jié)點(diǎn)和自由邊界節(jié)點(diǎn)的(譜元法基本公式已將自由邊界條件包含在內(nèi)),再引入物理邊界條件和人工邊界條件,就能通過(guò)時(shí)域逐步積分對(duì)上述方程進(jìn)行求解.其中,采用適當(dāng)?shù)娜斯み吔鐥l件,降低或消除人工邊界反射波的干擾,是保證波動(dòng)模擬精度的關(guān)鍵.
2 多次透射公式
有限模型人工邊界節(jié)點(diǎn)的位移由MTF進(jìn)行計(jì)算.MTF是一種直接以離散形式給出的一維化的時(shí)空外推公式,它由下式定義
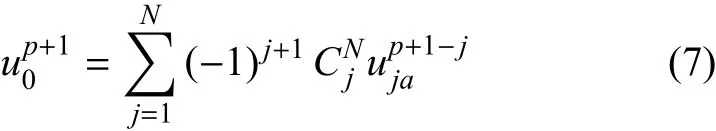
由于MTF計(jì)算點(diǎn)與內(nèi)域離散點(diǎn)位置不一定重合,上式無(wú)法直接用于波動(dòng)數(shù)值計(jì)算.只需通過(guò)適當(dāng)?shù)牟逯捣椒ǎ膳R近內(nèi)域離散點(diǎn)位移插值得到各個(gè)MTF計(jì)算點(diǎn)位移,就能得到適用于波動(dòng)數(shù)值模擬的MTF數(shù)值格式.
2.1 人工邊界附近的譜單元類型
在波動(dòng)有限元模擬中使用MTF時(shí),通常要求每個(gè)邊界節(jié)點(diǎn)的內(nèi)法線上有一系列等距分布的有限元節(jié)點(diǎn),然后利用這些節(jié)點(diǎn)進(jìn)行三點(diǎn)拋物線內(nèi)插和齊次內(nèi)插遞推方案,得到實(shí)用的MTF有限元格式[3435].其中包含兩個(gè)要點(diǎn),一是邊界法線,二是等距分布的有限元節(jié)點(diǎn).然而研究發(fā)現(xiàn):“法線”的條件不必嚴(yán)格滿足,但它必須是一條將人工邊界節(jié)點(diǎn)和一組內(nèi)域有限元節(jié)點(diǎn)串連起來(lái)的直線,這條直線通常是從邊界節(jié)點(diǎn)指向內(nèi)域的離散網(wǎng)格線;等距分布的有限元節(jié)點(diǎn)是保證齊次內(nèi)插過(guò)程得以實(shí)現(xiàn)的條件,因此在譜元不等距節(jié)點(diǎn)分布的條件下無(wú)法使用齊次內(nèi)插方案.
為了在譜元離散網(wǎng)格中實(shí)現(xiàn)一維化的MTF,首先需要確保每個(gè)人工邊界節(jié)點(diǎn)都對(duì)應(yīng)一條上述“直線”.如圖2所示的三角形譜單元和曲邊譜單元顯然不滿足這一要求,因?yàn)榍罢哂胁糠诌吔绻?jié)點(diǎn)上沒(méi)有指向內(nèi)域的離散網(wǎng)格線,而后者有大量的離散網(wǎng)格線為曲線.
如圖3所示的具有直線邊界的四邊形譜單元能夠滿足上述要求.同時(shí)由于譜單元尺寸較大,對(duì)于常用階次的MTF,其計(jì)算點(diǎn)一般不會(huì)超過(guò)一個(gè)譜單元范圍.于是對(duì)邊界附近的譜單元類型作如下假定:緊鄰人工邊界的一層譜單元為具有直線邊界的四邊形單元.

圖2 三角形譜單元和曲邊譜單元Fig.2 Triangleand curvilinear spectralelements
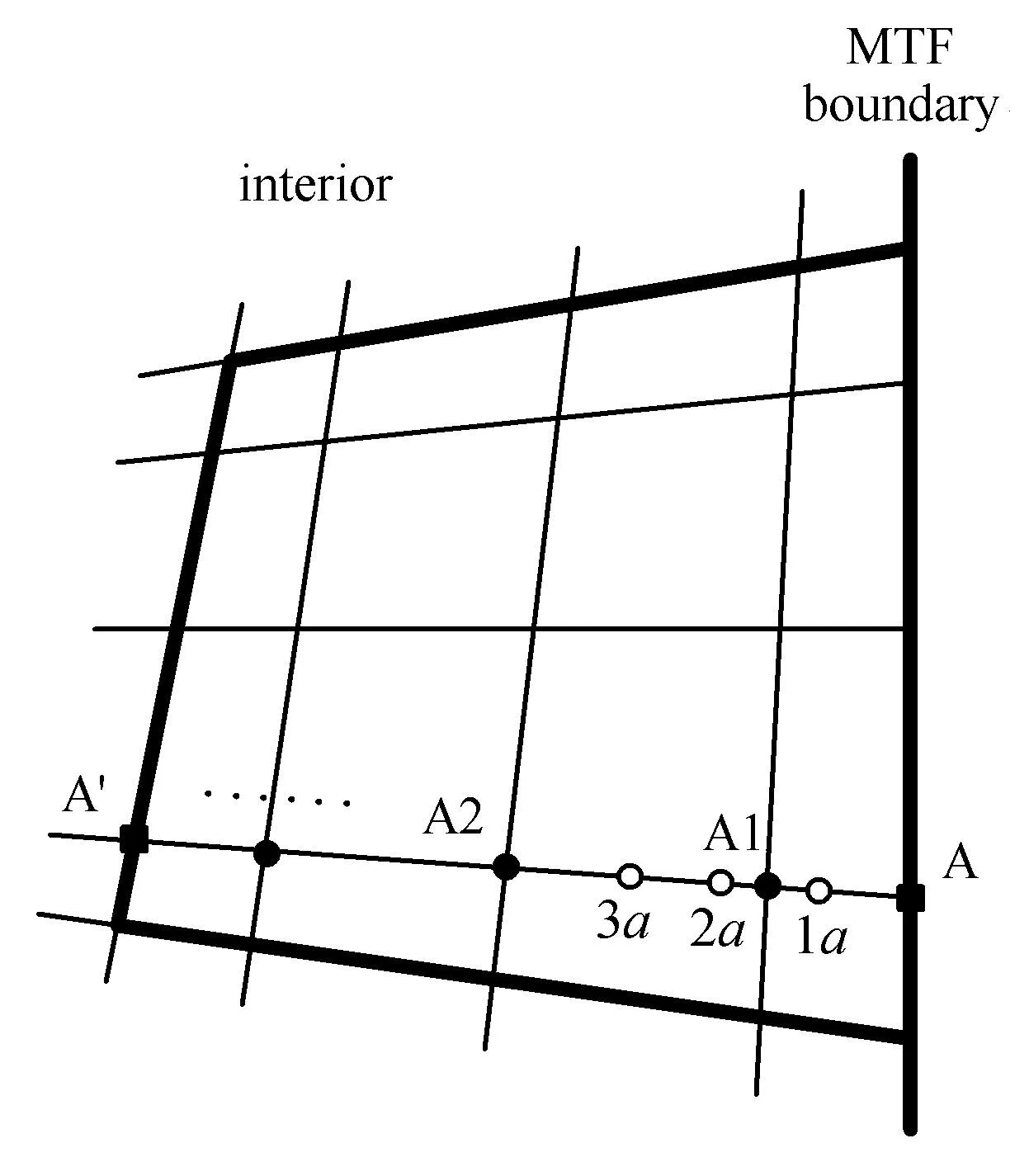
圖3 直邊譜單元中的MTF計(jì)算點(diǎn)Fig.3 Computation nodesofMTF in a spectralelementw ith straightedges
基于該假定,每個(gè)人工邊界節(jié)點(diǎn)的MTF計(jì)算點(diǎn)都位于一條指向內(nèi)域的離散網(wǎng)格線上,該點(diǎn)位移可由文獻(xiàn)[1]給出的MTF譜元格式進(jìn)行計(jì)算.
2.2 邊界位移計(jì)算公式
以圖3中A點(diǎn)為例來(lái)說(shuō)明在二維譜元離散網(wǎng)格中施加MTF的具體過(guò)程,其他人工邊界節(jié)點(diǎn)與之類似.A點(diǎn)指向內(nèi)域的離散網(wǎng)格線為一條直線,線上有不均勻分布的譜元節(jié)點(diǎn)A,A1,A2,···,A′,以及均勻分布的MTF計(jì)算點(diǎn)1a,2a,···,Na.各個(gè)MTF計(jì)算點(diǎn)分別位于不同的時(shí)刻,如圖4所示.
根據(jù)文獻(xiàn)[1]提出的MTF譜元格式,對(duì)各個(gè)MTF計(jì)算點(diǎn)的位移均采用同樣的拉格朗日多項(xiàng)式插值公式進(jìn)行計(jì)算,得到A點(diǎn)在p+1時(shí)刻的位移計(jì)算公式為
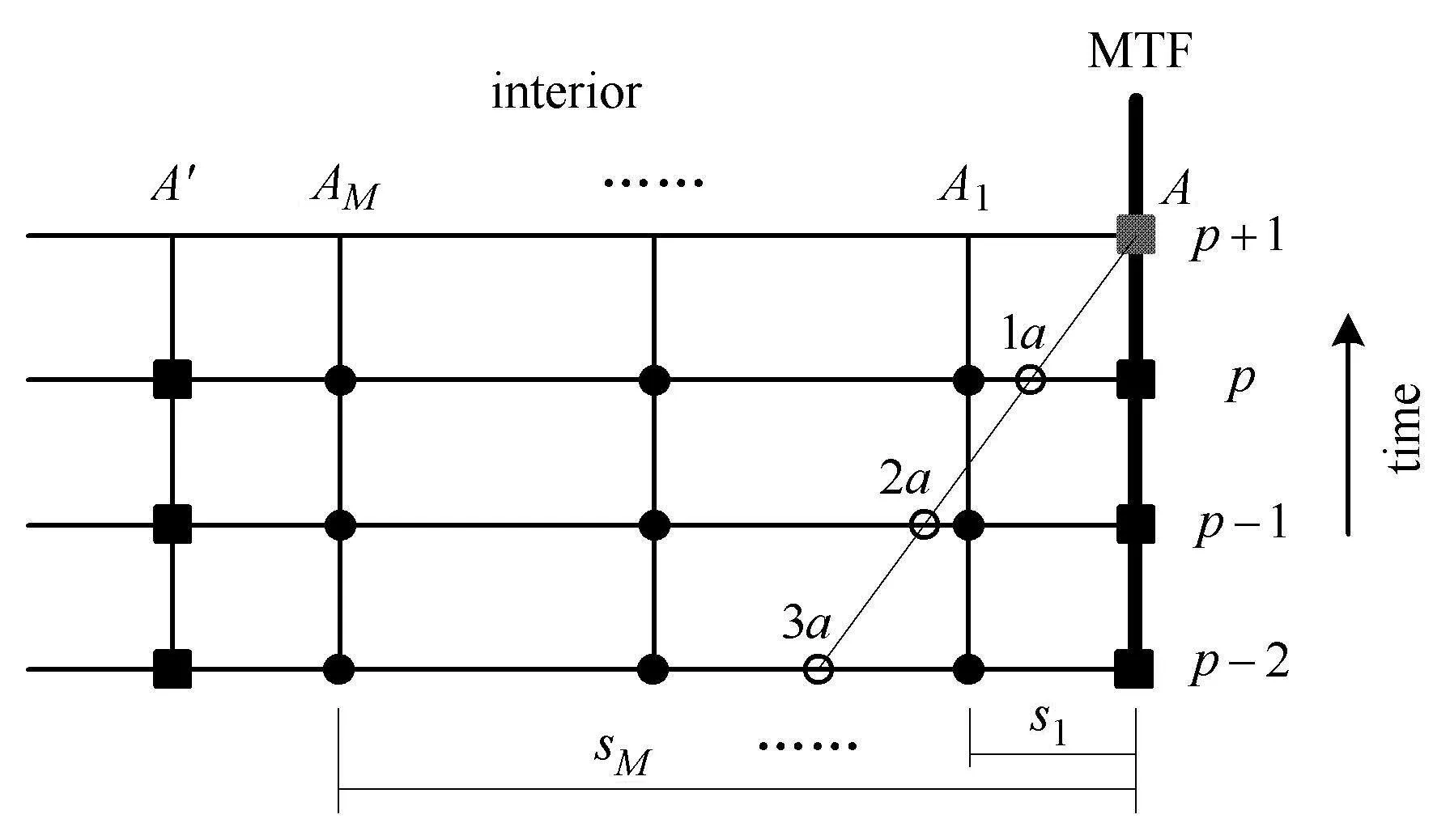
圖4 計(jì)算A點(diǎn)位移的MTF譜元格式Fig.4 SpectralelementschemeofMTF for computing the displacement of node A

式中,上標(biāo)T表示向量轉(zhuǎn)置,M為插值多項(xiàng)式階次.插值系數(shù)tj,0,tj,1,tj,2,···,tj,M與MTF計(jì)算點(diǎn)ja(j=1,2,···,N)和譜元網(wǎng)格點(diǎn)0,1,2,···,M一一對(duì)應(yīng).s0,s1,···,sM分別為節(jié)點(diǎn)A與A,A與A1,···,A與AM之間的距離.
插值多項(xiàng)式階次M的取值范圍為2,3,···,NEn;NEn為MTF計(jì)算方向的譜單元階次,因此式(8)~式(11)表示的是一系列MTF譜元格式.不同格式的區(qū)別在于采用的插值多項(xiàng)式階次M不同,即涉及的譜元離散點(diǎn)數(shù)目不同.其中,M=2時(shí)為三點(diǎn)拋物線內(nèi)插格式,M=NEn時(shí)為與譜單元位移模式一致的格式.式(8)~式(11)表示的MTF譜元格式能夠?qū)崿F(xiàn)的MTF階次范圍,由保證各個(gè)插值均為“內(nèi)插”的條件確定,為

可以看出,插值多項(xiàng)式階次M越高,能夠?qū)崿F(xiàn)的MTF階次N越高.對(duì)于最低的插值多項(xiàng)式階次M=2,通常N取為2和3,所以上式對(duì)常用的MTF階次一般不構(gòu)成限制.只有在少數(shù)極端情形下,如人工波速大大超過(guò)物理波速或透射階次很高時(shí),才需要驗(yàn)證.
上述MTF譜元格式是在較為稀疏的不等距譜元節(jié)點(diǎn)上進(jìn)行插值,用于計(jì)算各個(gè)MTF計(jì)算點(diǎn)1a,2a,···,Na位移的譜元節(jié)點(diǎn)數(shù)均為M+1個(gè);而傳統(tǒng)MTF有限元格式是在相對(duì)密集的等距有限元節(jié)點(diǎn)上進(jìn)行插值,用于計(jì)算各個(gè)MTF計(jì)算點(diǎn)1a,2a,···,Na位移的有限元節(jié)點(diǎn)數(shù)分別為3,5,7,···,2N+1個(gè).二者的主要區(qū)別在于實(shí)現(xiàn)高階MTF的方式不同,以及插值多項(xiàng)式階次不同.MTF有限元格式實(shí)現(xiàn)高階MTF的方式為齊次內(nèi)插遞推過(guò)程,這樣的好處是反射系數(shù)表達(dá)式為R=-fN,f為一階MTF的反射因子.此時(shí)各階MTF的穩(wěn)定界限相同,且在不失穩(wěn)的情況下,隨著透射階次N的增加,反射系數(shù)能夠穩(wěn)步地減小.MTF譜元格式使用簡(jiǎn)單內(nèi)插方案實(shí)現(xiàn)高階MTF,其模擬效果比齊次內(nèi)插方案有所降低,但是譜單元的高精度特性能夠較好地彌補(bǔ)這方面不足,而高階譜單元下插值多項(xiàng)式階次M的取值則是MTF譜元格式面臨的新問(wèn)題,對(duì)此文獻(xiàn)[1]已有初步討論,本文還將進(jìn)一步研究.
需要指出的是,上述MTF譜元格式和傳統(tǒng)MTF有限元格式都來(lái)源于MTF定義式(7),因此它們的模擬效果首先是由人工波速ca和透射階次N這兩個(gè)基本參數(shù)決定的.
3 方法可行性的驗(yàn)證
分別以無(wú)限均勻介質(zhì)中的外源和內(nèi)源SH波動(dòng)問(wèn)題為算例,驗(yàn)證本文方法的可行性.計(jì)算模型如圖5所示,模型所在區(qū)域?yàn)閷?00m、高400m的矩形,介質(zhì)物理波速c=400m/s,模型四邊均為MTF人工邊界.外源問(wèn)題的輸入波為從模型左下方斜入射的平面波,斜入射方向與豎軸夾角為α.內(nèi)源問(wèn)題的輸入波為作用在模型內(nèi)部某點(diǎn)的一個(gè)脈沖波源,波源位置距模型左側(cè)、下側(cè)邊界各100m.
輸入波位移時(shí)程采用Ricker型地震子波,具有表達(dá)式
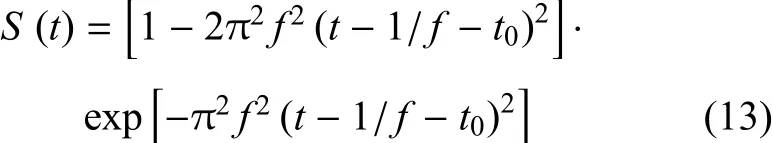
式中,f為中心頻率,t0為脈沖波形的起始時(shí)間.由此不難得出脈沖寬度為2/f,峰值頻率約為3f.計(jì)算時(shí)取f=10Hz,對(duì)應(yīng)峰值頻率約為30Hz.對(duì)于內(nèi)源問(wèn)題,上式為點(diǎn)波源的輸入波位移時(shí)程;對(duì)于外源問(wèn)題,上式僅為模型左下角點(diǎn)的輸入波位移時(shí)程,模型左側(cè)、下側(cè)邊界上其他節(jié)點(diǎn)的輸入波位移時(shí)程,需在上式的基礎(chǔ)上考慮相應(yīng)的滯后時(shí)間.
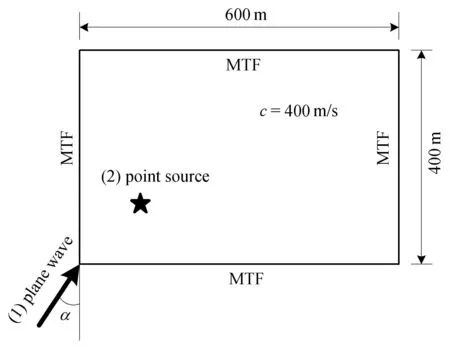
圖5 外源和內(nèi)源SH波動(dòng)問(wèn)題計(jì)算模型Fig.5 Computationmodelof SH-typewavemotion problem w ith outer or innerwave source
采用四階勒讓德譜單元對(duì)模型進(jìn)行空間離散,單元節(jié)點(diǎn)數(shù)為25,模型的單元數(shù)為1247(43×29=1247).兩個(gè)方向的譜單元尺寸分別為13.95m和13.79m,接近于λmin=400/30≈13.33m,符合譜元離散的精度要求.時(shí)間步長(zhǎng)取為0.003s,此時(shí),與時(shí)域積分穩(wěn)定性有關(guān)的庫(kù)朗數(shù)(Courantnumber)為q=c?t/?xmin=400×0.003/2.38≈0.50,小于臨界值(略小于1的某個(gè)常數(shù)),符合穩(wěn)定性要求.
3.1 外源問(wèn)題
首先進(jìn)行外源問(wèn)題的模擬.平面波入射角度設(shè)置為α=30°,此時(shí)外行波在上邊界和右邊界的透射角度(相對(duì)于邊界法線)分別為θ=30°和θ=60°.邊界條件采用式(8)~式(11)表示的MTF譜元格式,插值多項(xiàng)式階次取為M=4(與譜單元階次一致).采用不同邊界參數(shù)進(jìn)行數(shù)值模擬,選取其中比較有代表性的兩組結(jié)果,它們?cè)?.3s,0.6s,1.1s,1.4s的波場(chǎng)快照如圖6所示.
圖6(a)為第一組模擬結(jié)果,使用的邊界參數(shù)為:二階MTF,人工波速ca取為介質(zhì)物理波速c,這是MTF最常用的參數(shù)設(shè)置.前兩幅子圖顯示,在模型的左側(cè)和底部順利地實(shí)現(xiàn)了平面波的輸入,此時(shí)沒(méi)有外行波,邊界上不會(huì)發(fā)生反射.后兩幅子圖顯示,當(dāng)入射波到達(dá)右邊界和上邊界時(shí),MTF邊界能夠?qū)⒔^大部分外行波動(dòng)能量透射出去,僅有很小一部分能量被反射回計(jì)算區(qū)域.從圖中還可以看出,右邊界的反射明顯大于上邊界的反射,其原因在于右邊界為大角度透射(θ=60°),而上邊界的透射角度相對(duì)要小得多(θ=30°).這組模擬表明了本文提出的在二維譜元離散網(wǎng)格中使用MTF作為人工邊界條件的方法是可行的.對(duì)于透射角度不大的外行波,常用的MTF參數(shù)設(shè)置就能取得較好的模擬效果;對(duì)于透射角度較大的外行波,模擬效果有所降低.
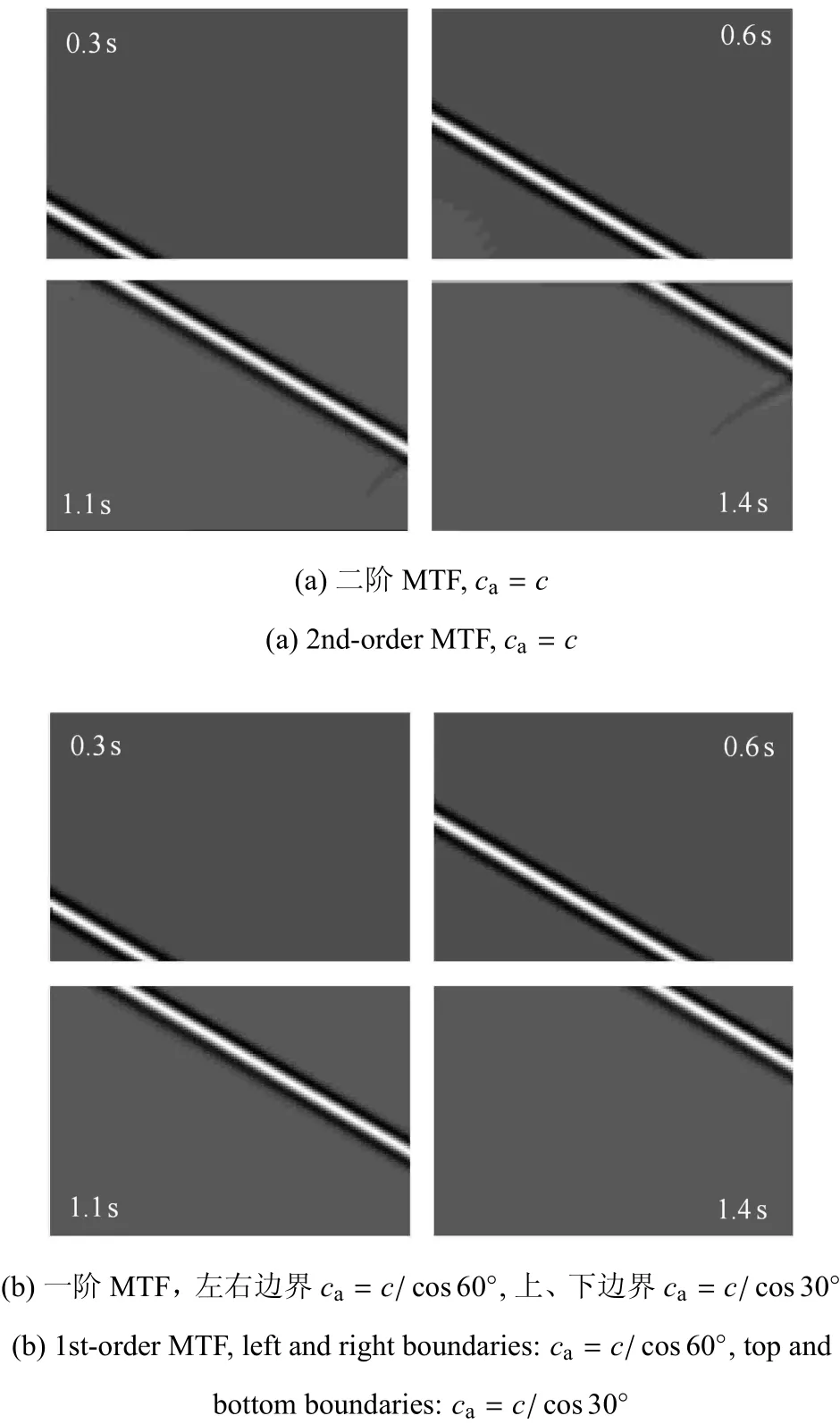
圖6外源問(wèn)題波場(chǎng)快照Fig.6 Wave fiel snapshotsof outer-source problem
圖6 (b)為第二組模擬結(jié)果,使用的邊界參數(shù)為:一階MTF,人工波速ca取為各邊的法向透射速度c/cosθ,即左、右邊界ca=2c,上、下邊界前兩幅子圖顯示平面波能夠在模型的左側(cè)和底部順利地輸入計(jì)算區(qū)域,與上一組相同.后兩幅子圖則顯示當(dāng)入射波到達(dá)模型右邊界和上邊界時(shí),能夠完全透射出去,不發(fā)生任何反射.這種近乎完美的模擬結(jié)果表明,通過(guò)調(diào)整人工波速取值,可以很好地克服僅由透射角度帶來(lái)的影響.這組模擬不僅驗(yàn)證了本文方法的可行性,還進(jìn)一步顯示了它在處理簡(jiǎn)單波動(dòng)問(wèn)題時(shí)的精確性.
平面波傳播問(wèn)題是一種理想化的波動(dòng)模型,波動(dòng)能量沿單一方向傳播的特性,使得每個(gè)人工邊界上外行波的視傳播速度都可以確定,這為設(shè)置人工邊界帶來(lái)了方便.實(shí)際波動(dòng)問(wèn)題則要復(fù)雜得多,其復(fù)雜性表現(xiàn)為由透射角度或波動(dòng)能量空間擴(kuò)散的衰減效應(yīng)導(dǎo)致的在人工邊界不同位置處,外行波的視傳播速度各不相同.對(duì)于這種復(fù)雜的實(shí)際波動(dòng)問(wèn)題,本文MTF譜元格式同樣能夠很好地模擬.
3.2 內(nèi)源問(wèn)題
接下來(lái)進(jìn)行內(nèi)源問(wèn)題的模擬.為顯示本文方法適應(yīng)復(fù)雜波場(chǎng)的能力,將波源設(shè)置在模型左下角以增加邊界附近波場(chǎng)的復(fù)雜性.此時(shí)對(duì)于左側(cè)和下側(cè)邊界,在靠近波源的位置會(huì)受到較為明顯的波場(chǎng)幾何衰減效應(yīng)的影響,遠(yuǎn)離波源的位置則存在外行波透射角度較大的問(wèn)題;上側(cè)和右側(cè)邊界受到的影響相對(duì)較小.采用式(8)~式(11)給出的MTF譜元格式,插值多項(xiàng)式階次取為M=4.由兩組不同邊界參數(shù)得到的0.3s,0.6s,0.9s,1.5s的波場(chǎng)快照如圖7所示.

圖7內(nèi)源問(wèn)題波場(chǎng)快照Fig.7 Wave fiel snapshotsof inner-source problem
圖7 (a)使用的是MTF常用的邊界參數(shù):二階MTF,ca=c,它對(duì)弱衰減、小角度透射的外行波模擬效果較好.圖中結(jié)果顯示在人工邊界各個(gè)位置處,大部分波動(dòng)能量都能夠順利透出,表明了本文MTF譜元格式模擬復(fù)雜波場(chǎng)問(wèn)題的有效性.僅有少量反射出現(xiàn)在左側(cè)、下側(cè)邊界距波源較近的波場(chǎng)衰減區(qū)和遠(yuǎn)端的大角度透射區(qū).如:0.6s子圖顯示了由于波場(chǎng)衰減效應(yīng)導(dǎo)致的未被完全透出的波;0.9s子圖中A點(diǎn)和B點(diǎn)反射波強(qiáng)度對(duì)比,表明本例的邊界參數(shù)設(shè)置對(duì)大角度外行波動(dòng)的模擬效果不如小角度外行波動(dòng);1.5s子圖中下邊界的反射波強(qiáng)度大于上邊界,因?yàn)橄逻吔绲耐干浣嵌雀?
為了保證水利工程的順利招標(biāo),我國(guó)出臺(tái)了各種法律法規(guī),以此來(lái)確保招標(biāo)工作開(kāi)展的科學(xué)性和合理性。但是,在實(shí)際的招標(biāo)過(guò)程中,仍然存在著不按照國(guó)家相應(yīng)的法律法規(guī)進(jìn)行招投標(biāo)的現(xiàn)象。尤其是有些小型企業(yè)在招標(biāo)的過(guò)程中進(jìn)行相應(yīng)的暗箱操作,這樣就在一定程度上打破了整個(gè)行業(yè)的競(jìng)爭(zhēng)平衡。而有些企業(yè)則是依靠人脈、金錢等進(jìn)行非法的招標(biāo),這樣不僅給公平、公正以及公開(kāi)的招標(biāo)環(huán)境造成了影響,而且還會(huì)影響招標(biāo)工作的順利展開(kāi)。
圖7(b)使用的邊界參數(shù)為:二階MTF,ca=c/cos45°,此時(shí)它對(duì)透射角度為45°左右的外行波模擬效果最好.由于本例中外行波在大部分人工邊界區(qū)域都是以一定角度透射的,所以不難預(yù)測(cè)采用45°角為透射中心,能夠顯著改善模型4個(gè)角點(diǎn)附近,以及左側(cè)、下側(cè)邊界上遠(yuǎn)離波源部分的透射效果.圖中結(jié)果顯示這組邊界參數(shù)的模擬效果總體上要優(yōu)于上組邊界參數(shù).如:0.9s子圖中B點(diǎn)的法向反射波依稀可見(jiàn),而A點(diǎn)附近接近45°角的反射波則幾乎被完全吸收;1.5s子圖中C點(diǎn)附近區(qū)域與上一組模擬結(jié)果相比,小角度反射波幾乎看不出差別,但是大角度反射波被吸收得更加充分.
內(nèi)源問(wèn)題算例不僅再次證明了本文方法的可行性,而且表明了它對(duì)復(fù)雜波動(dòng)問(wèn)題的適應(yīng)性,這種適應(yīng)性主要通過(guò)選取適當(dāng)?shù)倪吔鐓?shù)來(lái)實(shí)現(xiàn).就工程應(yīng)用而言,常用的MTF參數(shù)配置(N=2,ca=c)對(duì)很多實(shí)際波動(dòng)問(wèn)題已具有足夠的模擬精度.然而從研究角度看,深入研究MTF計(jì)算參數(shù)與波動(dòng)物理特征之間的聯(lián)系,根據(jù)外行波的視傳播規(guī)律有針對(duì)性地設(shè)定MTF計(jì)算參數(shù),對(duì)更好地求解復(fù)雜波動(dòng)問(wèn)題具有重要價(jià)值.
4 邊界反射誤差的時(shí)域分析
式(8)~式(11)描述的MTF譜元格式對(duì)外行波的透射效果受到插值多項(xiàng)式階次M、人工波速ca和透射階次N三個(gè)參數(shù)的影響,通過(guò)一組精心設(shè)計(jì)的SH波動(dòng)數(shù)值試驗(yàn),在時(shí)域內(nèi)定量地研究不同MTF參數(shù)取值下,本文MTF譜元格式在人工邊界上的反射誤差.
如圖8所示,采用兩個(gè)計(jì)算模型:半空間模型Ω2,左側(cè)使用式(8)~式(11)的MTF譜元格式,其余三側(cè)為自由邊界;全空間模型Ω3,四邊均為自由邊界.反射誤差的分析區(qū)域?yàn)棣?,這樣半空間模型的計(jì)算結(jié)果為受到左側(cè)人工邊界影響的數(shù)值解,全空間模型計(jì)算結(jié)果為不受任何邊界影響的大區(qū)域數(shù)值解(即精確解).介質(zhì)物理波速為1m/s,計(jì)算時(shí)間為2s,這組參數(shù)能夠保證計(jì)算時(shí)間內(nèi)自由邊界的反射波不會(huì)返回分析區(qū)域.

圖8 人工邊界反射誤差分析模型Fig.8 Numericalmodel for analyzing the reflectio errorof artificia boundary
為便于分析,本文模擬初始波場(chǎng)的自由擴(kuò)散問(wèn)題.由于沒(méi)有外部波動(dòng)能量輸入以及介質(zhì)阻尼等因素的干擾,模型中波動(dòng)能量的變化只受邊界影響.初始波場(chǎng)所在區(qū)域?yàn)閳D中圓形區(qū)域:圓心為(0.5,0),半徑為0.45m.分別采用三種具有不同傳播特征的初始波場(chǎng):圓形擴(kuò)散(circularspread)、法向透射(normal transmission)和45°角透射(45°transmission),其中圓形擴(kuò)散初始波場(chǎng)的表達(dá)式為如下高斯型脈沖
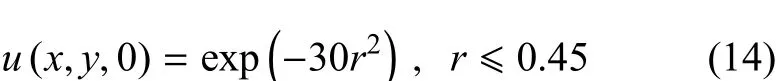
其中,r2=(x-0.5)2+y2.法向透射的初始波場(chǎng)由在上式右端乘以cos(8πx)得到,45°角透射的初始波場(chǎng)則通過(guò)在上式右端乘以cos(8πx-8πy)得到.根據(jù)公式λmin=1/kmax來(lái)確定3種初始波場(chǎng)中最短波長(zhǎng)成分,其中kmax為波數(shù)的上限值.由于初始波場(chǎng)是二維的,為簡(jiǎn)化分析,取波場(chǎng)變化最劇烈的方向進(jìn)行一維傅里葉分析,圓形擴(kuò)散情形計(jì)算exp(-30r2)的傅里葉譜,后兩種情形計(jì)算exp(-30r2)·cos(8πr)的傅里葉譜.得到圓形擴(kuò)散情形kmax的值約為4m-1,后兩種情形約為8m-1.3種情形的初始速度都為零.
x和y方向的譜單元階次均取為5,即采用36節(jié)點(diǎn)的單元.對(duì)于圓形擴(kuò)散初始波場(chǎng),單元尺寸取為1/4,對(duì)于法向透射和45°角透射初始波場(chǎng),單元尺寸取為1/7.區(qū)域Ω1內(nèi)的誤差波場(chǎng)定義為由半空間模型Ω2計(jì)算的數(shù)值解減去由全空間模型Ω3計(jì)算的精確解.衡量各個(gè)時(shí)刻MTF邊界反射誤差的指標(biāo)為:區(qū)域Ω1內(nèi)誤差波場(chǎng)的弗羅貝尼烏斯范數(shù)與初始波場(chǎng)的弗羅貝尼烏斯范數(shù)的比值.其中,各個(gè)時(shí)刻波動(dòng)位移矩陣U的弗羅貝尼烏斯范數(shù)的計(jì)算公式為
4.1 插值多項(xiàng)式階次的影響
3種初始波場(chǎng)情形下,MTF邊界上的反射誤差隨插值多項(xiàng)式階次M的變化規(guī)律如圖9所示(MTF計(jì)算參數(shù):N=2,ca=c,M=2,3,4,5).
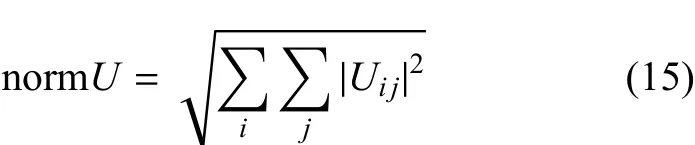

圖9 插值多項(xiàng)式階次M對(duì)反射誤差的影響Fig.9 Reflectio errorofMTFa ff ected by interpolation polynomial order M
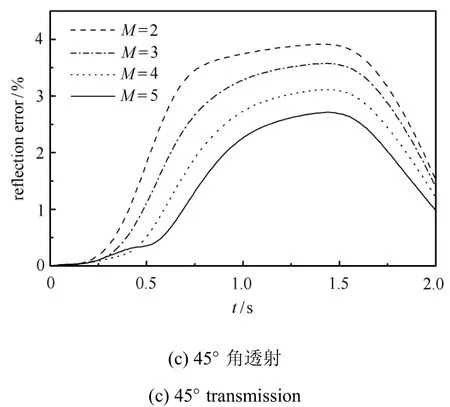
圖9插值多項(xiàng)式階次M對(duì)反射誤差的影響(續(xù))Fig.9 Reflectio errorofMTFa ff ected by interpolation polynom ial order M(continued)
圖9 結(jié)果顯示,人工邊界反射誤差隨著插值多項(xiàng)式階次M增加而逐步降低,其中,當(dāng)M=2時(shí)反射誤差最大,3種情形的峰值誤差均接近4%;當(dāng)M=5時(shí)反射誤差最小,3種情形下的峰值誤差分別為3.5%,0.9%和2.7%.顯然,當(dāng)插值多項(xiàng)式階次與譜單元階次一致時(shí),模擬效果最好.另外圖中結(jié)果還有兩點(diǎn)值得重視:一是所有反射誤差均在5%以內(nèi),這說(shuō)明如果從工程精度考慮,由插值多項(xiàng)式階次不同引起的誤差變化幾乎可以忽略不計(jì);二是不同插值多項(xiàng)式階次對(duì)透射方向比較單一的波動(dòng)問(wèn)題,如法向透射或45°角透射,具有層次較為分明的影響,而對(duì)透射方向比較豐富的波動(dòng)問(wèn)題,如圓形擴(kuò)散,其影響程度較小.
總之,插值多項(xiàng)式階次對(duì)透射效果的影響是在較高精度水平上的微小變化,它并不是決定式(8)~式(11)的MTF譜元格式模擬效果的關(guān)鍵因素.從實(shí)際使用角度出發(fā),考慮到邊界附近的譜單元階次會(huì)受到特定波動(dòng)問(wèn)題的模擬精度和計(jì)算效率的影響而有所不同,若存在多種不同插值多項(xiàng)式階次的邊界格式可供選擇,會(huì)大大增加問(wèn)題的復(fù)雜性,于是筆者建議統(tǒng)一采用插值多項(xiàng)式階次與譜單元階次一致的邊界格式.
4.2 人工波速的影響
3種初始波場(chǎng)情形下,MTF邊界上的反射誤差隨人工波速ca的變化規(guī)律如圖10所示(MTF計(jì)算參數(shù):N=2,M=5,α=ca/c,取值為0.5,0.75,1.0,1.25,1.5).
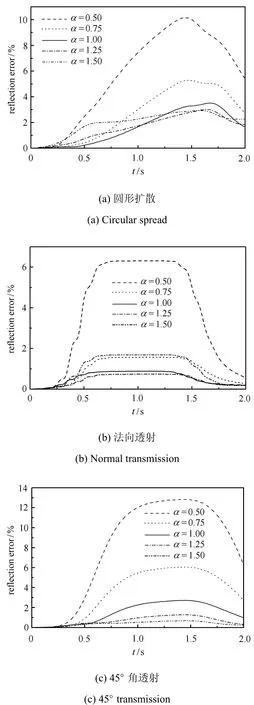
圖10 人工波速ca對(duì)反射誤差的影響Fig.10 Refection errorofMTFa ff ected by artificia wave speed ca
對(duì)比圖9和圖10結(jié)果可知,不同人工波速ca取值導(dǎo)致的邊界反射誤差變化幅度,大大超過(guò)不同插值多項(xiàng)式階次M導(dǎo)致的變化.這點(diǎn)不難理解,因?yàn)槿斯げㄋ偈荕TF定義式中的一個(gè)基本參數(shù).較大反射誤差出現(xiàn)在人工波速取值小于物理波速的情形,如ca=0.5c時(shí),峰值誤差分別達(dá)到10%,6.2%和13%,ca=0.75c時(shí),峰值誤差分別為5.3%,1.6%和6%.而當(dāng)人工波速取值等于或大于物理波速時(shí),反射誤差均處于較低水平,其峰值分別不超過(guò)3.5%,1.7%和2.7%.反射誤差越小,表明人工波速取值越接近外行波沿邊界法向的視傳播速度.
波動(dòng)問(wèn)題的復(fù)雜性在于受到透射角度、波幅衰減或多個(gè)子波疊加等因素的影響,確定外行波的視傳播速度常常比較困難,而且很多時(shí)候難以用一個(gè)值來(lái)精確地描述.但這部分研究能夠幫助我們認(rèn)識(shí)不同因素對(duì)視傳播速度的具體影響,進(jìn)而總結(jié)一些有助于優(yōu)化人工波速取值的結(jié)論.圖10(c)結(jié)果表明:外行波透射角度對(duì)視傳播速度的影響是較為確定的,以θ角透射的外行波的視傳播速度為c/cosθ.圖中模擬的是45°角透射波,其視傳播速度為α=1.5曲線與此最接近,因此反射誤差最小,其他α取值偏離越遠(yuǎn),反射誤差越大.圖10(b)模擬的是法向透射波,但反射誤差最小值沒(méi)有出現(xiàn)在α=1時(shí),這表明了初始波峰附近波動(dòng)能量幾何擴(kuò)散導(dǎo)致的波幅衰減效應(yīng)帶來(lái)的影響.從圖中結(jié)果不難看出,采用稍大于介質(zhì)物理波速的人工波速能夠有效地弱化這一影響,而本例中最優(yōu)人工波速取值在c和1.25c之間.圖10(a)結(jié)果顯示了單一人工波速的MTF譜元格式對(duì)實(shí)際復(fù)雜波動(dòng)問(wèn)題的模擬效果,它與不同時(shí)刻波動(dòng)能量在邊界上的透射區(qū)域和透射方向有關(guān).在1.0 s之前,法向和小角度透射波先到達(dá)邊界,此時(shí)人工波速等于c的模擬效果最好;在1.0s之后,大角度透射波成為主要成分,此時(shí)人工波速等于1.25c或1.5c的模擬效果要好于前者;而對(duì)于人工波速等于0.5c或0.75c的格式,其模擬效果自始至終都不理想.
以上分析表明,實(shí)際波動(dòng)問(wèn)題與理想的平面波法向透射問(wèn)題相比,存在透射角度或波幅衰減,二者都會(huì)導(dǎo)致視傳播速度增大,因此采用大于介質(zhì)物理波速的人工波速能夠達(dá)到更好的模擬效果.這一現(xiàn)象可理解為:從人工邊界節(jié)點(diǎn)的視角來(lái)看,存在透射角度或波幅衰減加速了波動(dòng)能量向人工邊界的“積聚”過(guò)程.由此可以推斷對(duì)于本例未涉及的多個(gè)子波疊加效應(yīng),其作用與前兩者相似.
至此,可將均勻介質(zhì)中標(biāo)量波問(wèn)題的人工波速取值規(guī)律總結(jié)為:不應(yīng)取小于介質(zhì)物理波速的值;對(duì)于大多數(shù)實(shí)際波動(dòng)問(wèn)題,取等于或稍大于介質(zhì)物理波速的值就能滿足要求;只有在少數(shù)特殊情形下,如透射角度較大、邊界距離點(diǎn)波源很近或較多子波場(chǎng)在邊界附近疊加時(shí),才可能需要采用大大超過(guò)介質(zhì)物理波速的值,但這往往會(huì)帶來(lái)諸如穩(wěn)定性等方面的問(wèn)題.
4.3 透射階次的影響
3種初始波場(chǎng)情形下,MTF邊界上的反射誤差隨透射階次N的變化規(guī)律如圖11所示(MTF計(jì)算參數(shù):M=5,ca=c,N=1,2,3).

圖11 透射階次N對(duì)反射誤差的影響Fig.11 Reflectio errora ff ected by transm itting order N
將圖11和圖10、圖9對(duì)比之后可以看出,透射階次N對(duì)邊界反射誤差的影響是決定性的,它大大超過(guò)了人工波速ca或插值多項(xiàng)式階次M的影響.其中,一階MTF的反射誤差較大,如圓形擴(kuò)散和45°角透射情形,峰值誤差分別為8.7%和10.2%,不滿足工程精度要求,說(shuō)明一階MTF難以用來(lái)模擬復(fù)雜波動(dòng)問(wèn)題.二階MTF的反射誤差顯著降低,三種情形下的峰值誤差分別為3.5%,0.9%和2.7%,都小于5%,滿足工程精度要求,說(shuō)明通常采用二階MTF進(jìn)行波動(dòng)模擬的做法是可取的.三階MTF的反射誤差沒(méi)有像預(yù)想的那樣進(jìn)一步降低,反而出現(xiàn)了不合理的增長(zhǎng),如圓形擴(kuò)散和法向透射情形,三階MTF的反射誤差大大超過(guò)一階MTF,45°角透射情形,三階MTF的反射誤差與二階MTF相當(dāng),但前者隨時(shí)間增長(zhǎng)的趨勢(shì)一直在延續(xù).我們還采用四階MTF進(jìn)行了模擬,其反射誤差已經(jīng)大到無(wú)法在圖中顯示的地步,更高階次的MTF同樣如此.這種現(xiàn)象表明N≥3時(shí)MTF邊界發(fā)生了某種失穩(wěn).
觀察三階MTF模擬的各個(gè)時(shí)刻波場(chǎng)變化,我們發(fā)現(xiàn)這是一種飄移失穩(wěn)[38],如圖12所示.飄移現(xiàn)象從MTF邊界中部開(kāi)始,逐漸向兩端擴(kuò)展,形成中間大、兩端小的拱形位移,拱的高度隨時(shí)間不斷上升,而實(shí)際邊界位移在主波形透過(guò)之后應(yīng)當(dāng)趨近于零.顯然,當(dāng)邊界出現(xiàn)這種嚴(yán)重的失穩(wěn)問(wèn)題時(shí),波動(dòng)模擬過(guò)程失敗.從實(shí)用角度看,不使用N≥3的MTF譜元格式就可以回避這個(gè)問(wèn)題,因?yàn)檫@里二階MTF沒(méi)有出現(xiàn)失穩(wěn),而且通常具有足夠的模擬精度.關(guān)于本文MTF譜元格式的飄移失穩(wěn)機(jī)理及其抑制措施,我們進(jìn)行了初步研究,已得到一些基本認(rèn)識(shí).
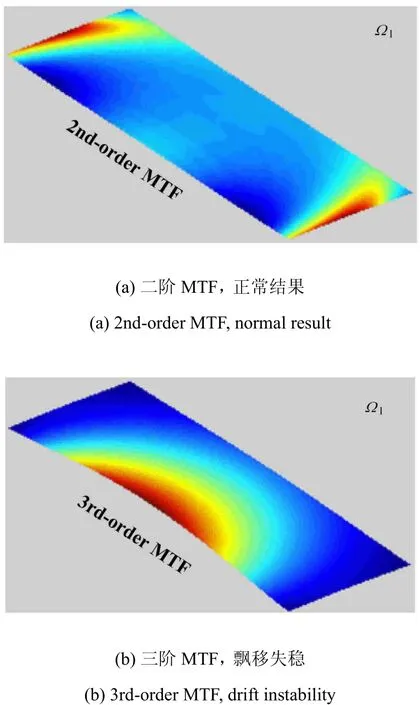
圖12 區(qū)域Ω1在2s時(shí)的波場(chǎng)Fig.12 Wave fiel of domainΩ1at2s
飄移失穩(wěn)現(xiàn)象不是本文MTF譜元格式所特有的,傳統(tǒng)MTF有限元格式可能出現(xiàn)飄移失穩(wěn)已是眾所周知[3841].而其他類型的人工邊界,如文獻(xiàn)[42]提出的幾種Higdon邊界形式,同樣可能出現(xiàn)飄移失穩(wěn).關(guān)于飄移失穩(wěn)機(jī)理目前還沒(méi)有統(tǒng)一的解釋,如:李小軍等[3839]認(rèn)為飄移失穩(wěn)是由于外源問(wèn)題采用連續(xù)介質(zhì)中的波動(dòng)理論解作為輸入波場(chǎng),而它與有限元離散解之間存在差異所造成的.周正華等[40-41]認(rèn)為是由于MTF不滿足GKS準(zhǔn)則導(dǎo)致數(shù)值解中的零頻和零波數(shù)成分可以通過(guò)邊界進(jìn)入計(jì)算區(qū),從而引起飄移失穩(wěn).Higdon[42]則將其解釋為邊界格式允許波動(dòng)模擬中出現(xiàn)關(guān)于零頻成分的廣義特征值.我們認(rèn)為這可能是由于人工邊界條件作為計(jì)算模型的支承條件本身就存在一定缺陷所致.
數(shù)值試驗(yàn)結(jié)果表明,本文MTF譜元格式可能出現(xiàn)飄移失穩(wěn)的透射階次,對(duì)于內(nèi)源問(wèn)題為N≥3,對(duì)于外源問(wèn)題為N≥2.其中,前者與文獻(xiàn)[42]的結(jié)果一致,后者則與文獻(xiàn)[38]結(jié)論相同.由此不難看出,飄移失穩(wěn)可能是邊界高階形式固有問(wèn)題,而當(dāng)邊界上存在外部波動(dòng)輸入時(shí),這一問(wèn)題更為嚴(yán)重.已有研究提出了幾種抑制MTF飄移失穩(wěn)的方法,如降低MTF階次[38]、在邊界區(qū)添加彈簧和阻尼元件[39],以及在MTF公式中增加一個(gè)微小正數(shù)[40].我們認(rèn)為這些方法都可以應(yīng)用到本文的MTF譜元格式當(dāng)中,這部分內(nèi)容值得深入探討,但已超出本文的范疇.
最后,對(duì)本文MTF譜元格式的高頻振蕩失穩(wěn)特性做一簡(jiǎn)要說(shuō)明.研究過(guò)程中我們進(jìn)行了大量SH波動(dòng)模擬,邊界均未出現(xiàn)高頻振蕩失穩(wěn).結(jié)合文獻(xiàn)[1]關(guān)于一維波動(dòng)問(wèn)題的研究,我們將其解釋為:本文MTF譜元格式的穩(wěn)定條件比內(nèi)域離散格式寬松,所以一般情況下不會(huì)發(fā)生高頻振蕩失穩(wěn),只有在人工波速大大超過(guò)介質(zhì)物理波速或透射階次很高時(shí),才有可能超出穩(wěn)定界限,在邊界上出現(xiàn)高頻振蕩失穩(wěn).
5 結(jié)論
(1)一維化的MTF公式需要通過(guò)一條直線上的離散網(wǎng)格點(diǎn)來(lái)實(shí)現(xiàn),本文通過(guò)假定緊鄰人工邊界的一層譜單元為直線邊界的四邊形單元,保證每個(gè)人工邊界節(jié)點(diǎn)都唯一地對(duì)應(yīng)一條指向內(nèi)域的離散網(wǎng)格線,用于實(shí)現(xiàn)文獻(xiàn)[1]所提出的MTF譜元格式.外源和內(nèi)源SH波動(dòng)問(wèn)題算例證實(shí)了方法的可行性以及對(duì)復(fù)雜波動(dòng)問(wèn)題的適應(yīng)性.
(2)插值多項(xiàng)式階次M對(duì)邊界反射誤差的影響較小,M取值較高的MTF譜元格式精度略好于M取值較低的格式.從使用方便的角度,我們建議M取值統(tǒng)一采用MTF計(jì)算方向的譜單元階次,這同時(shí)也是精度最好的選擇.
(3)人工波速ca取值對(duì)邊界反射誤差具有顯著影響.就本文研究的均勻介質(zhì)中SH波動(dòng)問(wèn)題而言,外行波存在透射角度、波幅衰減或多個(gè)子波場(chǎng)疊加,都會(huì)導(dǎo)致波動(dòng)能量更快地向邊界“積聚”,因此采用等于或稍大于介質(zhì)物理波速的人工波速能得到較好的模擬效果.采用小于或等于介質(zhì)物理波速的人工波速,推算邊界節(jié)點(diǎn)位移的準(zhǔn)確性較差.其他類型波動(dòng)問(wèn)題,如涉及到成層場(chǎng)地、P-SV波動(dòng),或Rayleigh面波等,情況較為復(fù)雜,可在此基礎(chǔ)上進(jìn)行專門討論.
(4)透射階次N對(duì)本文MTF譜元格式的模擬效果具有決定性影響.不發(fā)生失穩(wěn)時(shí),提高透射階次對(duì)降低反射誤差的效果最為明顯.但是,高階MTF容易出現(xiàn)飄移失穩(wěn),其中,內(nèi)源問(wèn)題和外源問(wèn)題開(kāi)始出現(xiàn)飄移失穩(wěn)的MTF階次分別為3和2.
1邢浩潔,李鴻晶.透射邊界條件在波動(dòng)譜元模擬中的實(shí)現(xiàn):一維波動(dòng).力學(xué)學(xué)報(bào),2017,49(2):367-379(Xing Haojie,LiHongjing.Implementation ofmulti-transm itting boundary condition for thewave motion simulation by spectralelementmethod:onedimension case.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(2):367-379(in Chinese))
2 Patera AT.A spectral elementmethod for flui dynam ics:Lam inar fl w in a channelexpansion.JournalofComputational Physics,1984,54(3):468-488
3 Priolo E,SerianiG.A numerical investigation of Chebyshev spectral elementmethod for acoustic wave propagation//Proceedings of the13th IMACSConferenceon Comparative Applied Mathematics,Dublin,Ireland,1991,2:551-556
4 SerianiG,Priolo E.Spectralelementmethod foracousticwavesimulation in heterogeneousmedia.Finite Elements in Analysis and Design,1994,16(3):337-348
5 Seriani G.A parallel spectral elementmethod for acoustic wave modeling.JournalofComputationalAcoustics,1997,5(1):53-69
6 SerianiG,Su Chang.Wave propagationmodeling in highly heterogeneousmedia by a ploy-grid Chebyshev spectralelementmethod.JournalofComputationalphysics,2012,20(2):345-351
7 Komatitsch D,Vilotte JP.The spectralelementmethod:an e ffi cient tool to simulate theseism ic responseof 2D and 3D geologicalstructures.Bulletin ofthe SeismologicalSociety ofAmerica,1998,88(2):368-392
8 Komatitsch D,Vilotte JP,VaiR,etal.The spectralelementmethod for elastic wave equations—application to 2-D and 3-D seism ic problems.International Journal for Numerical Methods in Engineering,1999,45(9):1139-1164
9 Komatitsch D,Barnes C,Tromp J.Wave propagation near a flui solid interface:a spectral-element approach.Geophysics,2000,65(2):623-631
10 Komatitsch D,Liu Qinya,Tromp J,et al.Simulations of ground motion in the Los Angeles basin based upon the spectral-element method.Bulletin of the Seismological Society of America,2004,94(1):187-206
11王秀明,SerianiG,林偉軍.利用譜元法計(jì)算彈性波場(chǎng)的若干理論問(wèn)題.中國(guó)科學(xué):G輯,2007,37(1):1-19(Wang Xium ing,SerianiG,Lin Weijun.Several theoretic aspects for the calculation of elasticwave fiel using spectralelementmethod.Science China(G series),2007,37(1):1-19(in Chinese))
12嚴(yán)珍珍,張懷,楊長(zhǎng)春等.汶川大地震地震波傳播的譜元法數(shù)值模擬研究.中國(guó)科學(xué):D輯,2009,39(4):393-402(Yan Zhenzhen,Zhang Huai,Yang Changchun,et al.Numerical investigation of seismic wave propagation of Wenchuan Earthquake using spectral elementmethod.Science China(D series),2009,39(4):393-402(in Chinese))
13李孝波.基于譜元法的玉田震害異常研究.[博士論文].哈爾濱:中國(guó)地震局工程力學(xué)研究所,2014(Li Xiaobo.The investigation of seism ic damage anomaly in Yutian based on spectral element method.[PhD Thesis].Harbin:Institute of Engineering Mechanics,Chinese Earthquake Adm inistration,2014(in Chinese))
14李孝波,薄景山,齊文浩等.地震動(dòng)模擬中的譜元法.地球物理學(xué)進(jìn)展,2014,29(5):2029-2039(LiXiaobo,Bo Jingshan,QiWenhao,etal.Spectralelementmethod in seism ic groundmotion simulation.Progress in Geophysics,2014,29(5):2029-2039(in Chinese))
15劉有山,滕吉文,徐濤等.三角網(wǎng)格譜元法地震波場(chǎng)數(shù)值模擬.地球物理學(xué)進(jìn)展,2014,29(4):1715-1726(Liu Youshan,Teng Jiwen,Xu Tao,etal.Numericalmodeling of seism ic wave fiel w ith the SEM based on triangles.Progress in Geophysics,2014,29(4):1715-1726(in Chinese))
16李琳,劉韜,胡天躍.三角譜元法及其在地震正演模擬中的應(yīng)用.地球物理學(xué)報(bào),2014,57(4):1224-1234(Li Lin,Liu Tao,Hu Tianyue.Spectral elementmethod w ith triangularmesh and its application in seismicmodeling.Chinese Journal ofGeophysics,2014,57(4):1224-1234(in Chinese))
17李洪建,韓立國(guó),鞏向博.復(fù)雜構(gòu)造網(wǎng)格化及高精度地震波場(chǎng)譜元法數(shù)值模擬.石油物探,2014,53(4):375-383(LiHongjian,Han Liguo,Gong Xiangbo.High precision spectral elementmethod based on grid discretization of complicated structure for seism ic wavefiel numerical simulation.Geophysical Prospecting for Petroleum,2014,53(4):375-383(in Chinese))
18曹丹平,周建科,印興耀.三角網(wǎng)格有限元法波動(dòng)模擬的數(shù)值頻散及穩(wěn)定性研究.地球物理學(xué)報(bào),2015(5):1717-1730(Cao Danping,Zhou Jianke,Yin Xingyao.The study for numerical dispersion and stability ofwavemotion w ith triangle-based finit element algorithm.Chinese JournalofGeophysics,2015(5):1717-1730(in Chinese))
19 He Chunhui,Wang Jinting,Zhang Chuhan.Nonlinear spectralelementmethod for 3D seismic-wave propagation.Bulletin of the Seismological Society ofAmerica,2016,106(3):1074-1087
20林燈,崔濤,冷偉等.一種求解地震波方程的高效并行譜元格式.計(jì)算機(jī)研究與發(fā)展,2016,53(5):1147-1155(Lin Deng,Cui Tao,Leng Wei,et al.An e ffi cient parallel spectral element scheme for solving seism ic wave equation.JournalofComputer Research and Development,2016,53(5):1147-1155(in Chinese))
21 Liu Youshan,Teng Jiwen,Lan Haiqiang,etal.A comparativestudy of finit elementand spectralelementmethods in seism ic wavefiel modeling.Geophysics,2014,79(2):T91-T104
22 Chen Yushu,Yang Guangwen,Ma Xiao,et al.A time-space domain stereo finit di ff erencemethod for3D scalarwavepropagation.Computers&Geosciences,2016,96:218-235
23 Liu Shaolin,LiXiaofan,WangWenshuai,etal.Am ixed-grid finit elementmethod w ith PML absorbing boundary conditions for seism ic wavemodelling.Journal ofGeophysics&Engineering,2014,11(5):1-13
24 Clayton R,EngquistB.Absorbing boundary conditions for acoustic and elastic waveequations.Bulletin ofthe Seismological Society of America,1977,67(6):1529-1540
25 Keller JB,Dan G.Exactnon-reflectin boundary conditions.JournalofComputational Physics,1989,82(1):172-192
26 Chaljub E,Komatitsch D,Vilotte JP,etal.Spectral-elementanalysis in seismology.Advances in Geophysics,2007,48:365-419
27 He Ying,M in M isun,Nicholls DP.A spectralelementmethod w ith transparentboundary condition for periodic layered media scattering.JournalofScientifi Computing,2016,68(2):772-802
28趙密.近場(chǎng)波動(dòng)有限元模擬的應(yīng)力型時(shí)域人工邊界條件及其應(yīng)用.[博士論文].北京:北京工業(yè)大學(xué),2009(Zhao M i.Stress-type time-domain artificia boundary condition for finite-elemen simulation ofnear-fiel wavemotion and itsengineering application.[PhD Thesis].Beijing:Beijing University of Technology,2009(in Chinese))
29 Berenger JP.A perfectlymatched layer for theabsorption ofelectromagnetic waves.Journal ofComputational Physics,1994,114(2):185-200
30 Komatitsch D,Tromp J.A perfectlymatched layerabsorbingboundary condition for thesecond-order seism icwaveequation.Geophysical Journal International,2003,154(1):146-153
31 Martin R,Komatitsch D,Gedney SD.A variational formulation of a stabilized unsplit convolutional perfectly matched layer for the isotropic or anisotropic seism ic wave equation.Computer Modeling in Engineering&Sciences,2008,37(3):274-304
32廉西猛,單聯(lián)瑜,隋志強(qiáng).地震正演數(shù)值模擬完全匹配層吸收邊界條件研究綜述.地球物理學(xué)進(jìn)展,2015,30(4):1725-1733(Kang Ximeng,Shan Lianyu,Sui Zhiqiang.An overview of research on perfectly matched layers absorbing boundary condition of seismic forward numericalsimulation.Progress in Geophysics,2015,30(4):1725-1733(in Chinese))
33 Xie Zhinan,Matzen R,Cristini P,etal.A perfectlymatched layer for fluid-soli problems:Application to ocean-acousticssimulations w ith solid oceanbottoms.Journalofthe AcousticalSociety ofAmerica,2016,140(1):165-175
34廖振鵬,黃孔亮,楊柏坡等.暫態(tài)波透射邊界.中國(guó)科學(xué):A輯,1984,(6):556-564(Liao Zhenpeng,Huang Kongliang,Yang Baipo,et al.A transm itting boundary for transientwave.Scientia Sinica(SeriesA),1984,(6):556-564(in Chinese))
35 Liao Zhenpeng,Wong Hongliang.A transm itting boundary for the numerical simulation of elastic wave propagation.International JournalofSoilDynamicsand Earthquake Engineering,1984,3(4):174-183
36戴志軍,李小軍,侯春林.譜元法與透射邊界的配合使用及其穩(wěn)定性研究.工程力學(xué),2015,32(11):40-50(Dai Zhijun,Li Xiaojun,Hou Chunlin.A combination usageof transm itting formulaand spectral elementmethod and the study of its stability.Engineering Mechanics,2015,32(11):40-50(in Chinese))
37陳少林,趙宇昕.一種三維飽和土--基礎(chǔ)--結(jié)構(gòu)動(dòng)力相互作用分析方法.力學(xué)學(xué)報(bào),2016,48(6):1362-1371(Chen Shaolin,Zhao Yuxin.A method for three-dimensional saturated soil-foundationstructure dynam ic interaction analysis.Chinese JournalofTheoreticaland Applied Mechanics,2016,48(6):1362-1371(in Chinese))
38李小軍,廖振鵬.時(shí)域局部透射邊界的計(jì)算飄移失穩(wěn).力學(xué)學(xué)報(bào),1996,28(5):627-632(LiXiaojun,Liao Zhenpeng.Thedriftinstability of local transmitting boundary in time domain.Acta Mechanica Scinica,1996,28(5):627-632(in Chinese))
39李小軍,楊宇.透射邊界穩(wěn)定性控制措施探討.巖土工程學(xué)報(bào),2012,34(4):641-645(LiXiaojun,Yang Yu.Measures for stability controlof transmitting boundary.Chinese Journal ofGeotechnical Engineering,2012,34(4):641-645(in Chinese))
40周正華,廖振鵬.消除多次透射公式飄移失穩(wěn)的措施.力學(xué)學(xué)報(bào),2001,33(4):550-554(Zhou Zhenghua,Liao Zhenpeng.A measure for eliminating drift instability of the multi-transmitting formula.Acta Mechanica Scinica,2001,33(4):550-554(in Chinese))
41廖振鵬,周正華,張艷紅.波動(dòng)數(shù)值模擬中透射邊界的穩(wěn)定實(shí)現(xiàn).地球物理學(xué)報(bào),2002,45(4):533-545(Liao Zhenpeng,Zhou Zhenghua,Zhang Yanhong.Stable implementation of transm itting boundary in numericalsimulation ofwavemotion.Chinese Journal ofGeophysics,2002,45(4):533-545(in Chinese))
42 Higdon RL.Absorbing boundary conditions for di ff erence approximations to themulti-dimensionalwave equation.Mathematics of Computation,1986,47(176):437-459
43景立平.多次透射公式實(shí)用形式穩(wěn)定性分析.地震工程與工程振動(dòng),2004,24(4):20-24(Jing Liping.Stability analysis of practical formula formulti-transm itting boundary.Earthquake Engineering and Engineering Vibration,2004,24(4):20-24(in Chinese))
44章旭斌,廖振鵬,謝志南.透射邊界高頻耦合失穩(wěn)機(jī)理及穩(wěn)定實(shí)現(xiàn)——SH波動(dòng).地球物理學(xué)報(bào),2015,58(10):3639-3648(Zhang Xubin,Liao Zhenpeng,Xie Zhinan.Mechanism ofhigh frequency coupling instability and stable implementation for transmitting boundary——SH wavemotion.Chinese Journal ofGeophysics,2015,58(10):3639-3648(in Chinese))
IMPLEMENTATIONOFMULTI-TRANSM ITTING BOUNDARY CONDITION FOR WAVEMOTION SIMULATION BY SPECTRAL ELEMENTMETHOD:TWO DIMENSION CASE1)
Xing Haojie LiHongjing2)
(College ofCivilEngineering,Nanjing Tech University,Nanjing 211816,China)
Thespectralelementschemeofmulti-transm itting formula(MTF)which proposed by Xing and Liisdeveloped and expanded to numerical simulation of SH-typewavemotion in homogeneous linearmedium.The spectral elements adjacent to the artificia boundariesare supposed to be rectilinear quadrilateralelements,in order thateach node on the artificia boundary locates on a unique grid line pointing to the interior domain,hence the displacementof a particular artificia boundary node at a certain time can be inferred from displacements of nodes on the grid line atearlier times.Two numericalexamples,the planewave propagationw ith a certain angle(outer-source problem)and the free spread ofa pulsewaveoriginated from a point(inner-source problem),areemployed for verificatio of thiswavemotion simulationprocedurewhich combines the spectral elementmethod w ith MTF boundary.Themain parameters a ff ecting reflectio error of the MTF scheme,such as order of interpolation polynom ial,artificia wave speed and transm itting order,are investigated in time domain via a seriesof initial-value problems.The results show that the order of interpolation polynomial influence the reflectio error very little,while higher interpolation ordermay lead to better accuracy.For the choice of artificia wave speed,it is preferable to choose values equal or slightly greater than the physicalwave speed,otherw ise bigger reflectio errors come about.Transm itting order exerts themost significan impacton reflectio error,which would be reduced greatly with the increase of transm itting order of MTF,but the undesired drift instabilitymay arisewhen transmitting order reaches three or two for inner-source and outer-source problems,respectively.Although thework combining MTF boundary w ith spectralelementmethod is conducted on simulation of SH wave propagation in infinit homogeneousmedium in thispaper,ithas laid the foundation of research onmore complicated situations,such as issuesof layered soilsites,propagation of P-SV waveorRayleighwave,etc.
multi-transm itting formula,spectral elementmethod,SH-type wavemotion,spectral element scheme of MTF,drift instability
P315
A
10.6052/0459-1879-16-393
2016-12-25收稿,2017-03-01錄用,2017-03-06網(wǎng)絡(luò)版發(fā)表.
1)國(guó)家自然科學(xué)基金資助項(xiàng)目(51278245).
2)李鴻晶,教授,主要研究方向:地震工程學(xué).E-mail:hjing@njtech.edu.cn
邢浩潔,李鴻晶.透射邊界條件在波動(dòng)譜元模擬中的實(shí)現(xiàn):二維波動(dòng).力學(xué)學(xué)報(bào),2017,49(4):894-906
Xing Haojie,LiHongjing.Implementation ofmulti-transm itting boundary condition forwavemotion simulation by spectral element method:two dimension case.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(4):894-906

