曲線加筋Kirchho ff-M ind lin板自由振動分析1)

劉璟澤姜東韓曉林費慶國

?(東南大學工程力學系,南京210096)?(東南大學空天機械動力學研究所,南京211189)??(南京林業大學機械電子工程學院,南京210037)

動力學與控制

曲線加筋Kirchho ff-M ind lin板自由振動分析1)

劉璟澤?,?姜東?,??韓曉林?費慶國?,2)

?(東南大學工程力學系,南京210096)?(東南大學空天機械動力學研究所,南京211189)??(南京林業大學機械電子工程學院,南京210037)

相比傳統加筋板，曲線加筋板能夠更充分地發揮材料力學性能.在加筋板力學分析中，厚板通常采用Reissner-M indlin理論，然而當板厚較薄時易出現剪切自鎖，離散的Kirchho ff-M indlin理論采用假設剪切應變場可避免該問題.針對曲線加筋Kirchho ff-M indlin板自由振動分析，采用離散的Kirchho ff-M indlin三角形單元和Timoshenko曲梁單元分別模擬板和加強筋，根據板的位移插值函數及筋板交界面的位移協調條件，建立基于板單元位移自由度的有限元方程.為了驗證方法的有效性和準確性，采用直線加筋薄板、曲線加筋薄板和厚板3種模型進行算例研究，通過收斂性和精度分析來選擇合理的有限元網格密度.直線加筋薄板前20階固有頻率均與文獻結果吻合良好；曲線加筋板算例中，本文方法滿足收斂條件的板單元數目為2469，Nastran模型板單元數目為6243；本文所得曲線加筋板固有頻率與Nastran計算結果最大誤差為3.4%.研究結果表明，本文方法無需筋板單元共節點，可使用較少的有限元網格數量，并能夠保證計算精度；在離散Kirchho ff-M indlin三角形板單元基礎上構造Timoshenko梁單元可同時適用于曲線加筋薄板與厚板自由振動分析.

曲線加筋，Kirchho ff-M indlin板，自由振動分析

引言

加筋結構在同等重量條件下具有更加出色的力學性能，已廣泛應用于航空航天、船舶、汽車等領域.傳統的加筋板/殼多采用橫向、縱向或按照特定角度鋪設筋條，并不能最大限度地發揮材料性能.Kapania等[1]提出了曲線筋的概念，曲線加筋可有效考慮局部性能，更利于結構的優化設計.

在加筋板有限元建模中，當筋條形狀發生改變時，為使筋板節點一致，必須對筋節點重新劃分單元.為了克服這種困難，許多研究者提出在有限元分析中使用等參單元對筋板分別建模，然后利用板單元的節點近似表達筋單元節點.Mukhopadhyay等[2]進行了偏心加筋板的自由振動分析.通過有限元方法中的插值函數，利用筋板接觸面的位移協調條件，使得筋的位移和幾何坐標可以用板的形式表達.因此，加強筋可以被布置在板單元內的任意位置，無需沿著板的節點線布置.Ghosh和Biswal[3-4]使用四節點矩形單元模擬板單元，加強筋單元剛度矩陣用筋節點所在的四節點板單元來表達.Kumar和Mukhopadhyay[5]使用梁單元對加強筋來建模.梁單元的節點位移和坐標被其所在板的殼單元節點位移和坐標插值得到.此模型被廣泛應用于加筋板結構的靜力分析[67]，屈曲分析[810]，自由振動分析和瞬態動力學分析[11-15].

關于加強筋的建模方法，經歷了一段時期的發展，早期線性插值函數被用來模擬加強筋，但事實證明它會導致較大的位移、應力誤差[16]，隨后，科研工作者采取增加節點自由度、增加插值函數的階數來提高模擬精度[17].近來，人們多采用3節點梁單元，對加強筋進行建模[1820].

為了對加筋板的板單元建模，基于Kirchho ff薄板理論，Barik等[21]結合四節點矩形平面應力單元和板彎曲單元進行了加筋板的靜力、自由振動和前屈曲分析.基于Reissner-M indlin厚板理論，Mukheriee和Mukhoadhyay[22]使用等參單元進行加筋板自由振動和屈曲分析.Holopainen[23]應用混合插值彎曲板單元進行加筋板的自由振動分析，可以有效避免剪切鎖死，且具有較好收斂性.Nguyen-Thoi等[24]基于平滑離散剪切間隙方法，將板單元和膜元結合，并使用厚梁單元模擬筋條進行了加筋板的自由振動分析.章向明等[2526]構造了用于復合材料偏心加筋板、殼結構大變形分析的板、殼單元，此模型將肋骨連同板、殼視為一個單元，即偏心加筋板、殼單元，同時考慮了幾何非線性和剪切變形.張志峰等[27]基于精細三角形M indlin板單元構造了21個自由度三角形復合材料加筋板、殼單元，并將其應用于加筋板、殼結構振動、屈曲的分析.

Katili[28]基于Reissner-M indlin板理論和假設剪切應變場提出了一種離散的Kirchho ff-M indlin三角形彎曲板單元DKMT，這種單元同時適用于厚板與薄板分析，可以避免剪切鎖死和零能模式.

本文使用DKMT單元作為板單元，采用網格劃分工具DistMesh[29]生成板的有限元網格，鐵木辛柯梁單元作為筋單元，利用三階B-Spline曲線對加強筋進行幾何建模.筋板單元無需共節點，加強筋可以在板內任意布置.本文首先進行了收斂性研究，將直線加筋板頻率結果與文獻結果進行對比驗證，得出了收斂的有限元模型；其次分別分析了薄板和厚板情況下的曲線加筋板固有頻率和振型，并與Nastran分析結果進行對比.

1 離散K irchho ff-M ind lin三角形單元

1.1 位移場

離散Kirchho ff-M indlin三角形單元(discreteKirchho ff-M indlin triangular,DKMT)是一種包含橫剪切效應的彎曲板單元,結合文獻[30]中對板單元內撓度場定義，單元內任意一點撓度和法線轉角可以表達為

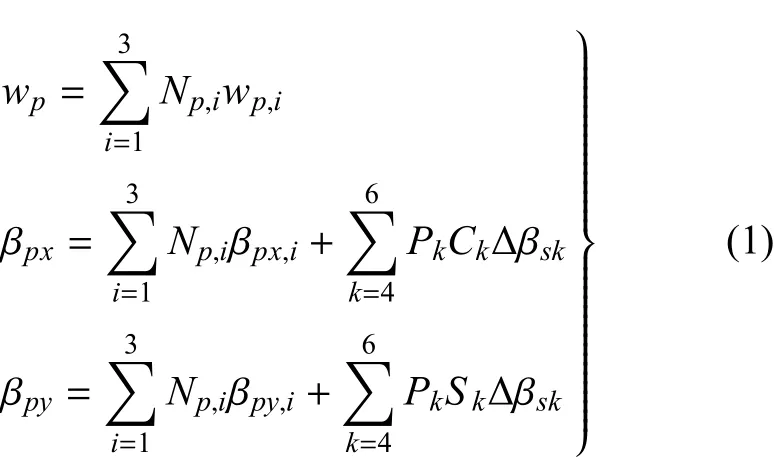
其中，Np,1=λ，Np,2=ξ，Np,3=η，Pk表示一組高階函數，P4=4λξ，P5=4ξη，P6=4λη，λ=1-ξ-η.wp,i是1,2,3節點的撓度，βpx,i和βpy,i是1,2,3節點的轉角，?βsk是中點4,5,6的轉角.Ck和Sk是三角形邊與x軸所成角度的余弦和正弦值.單元如圖1所示.

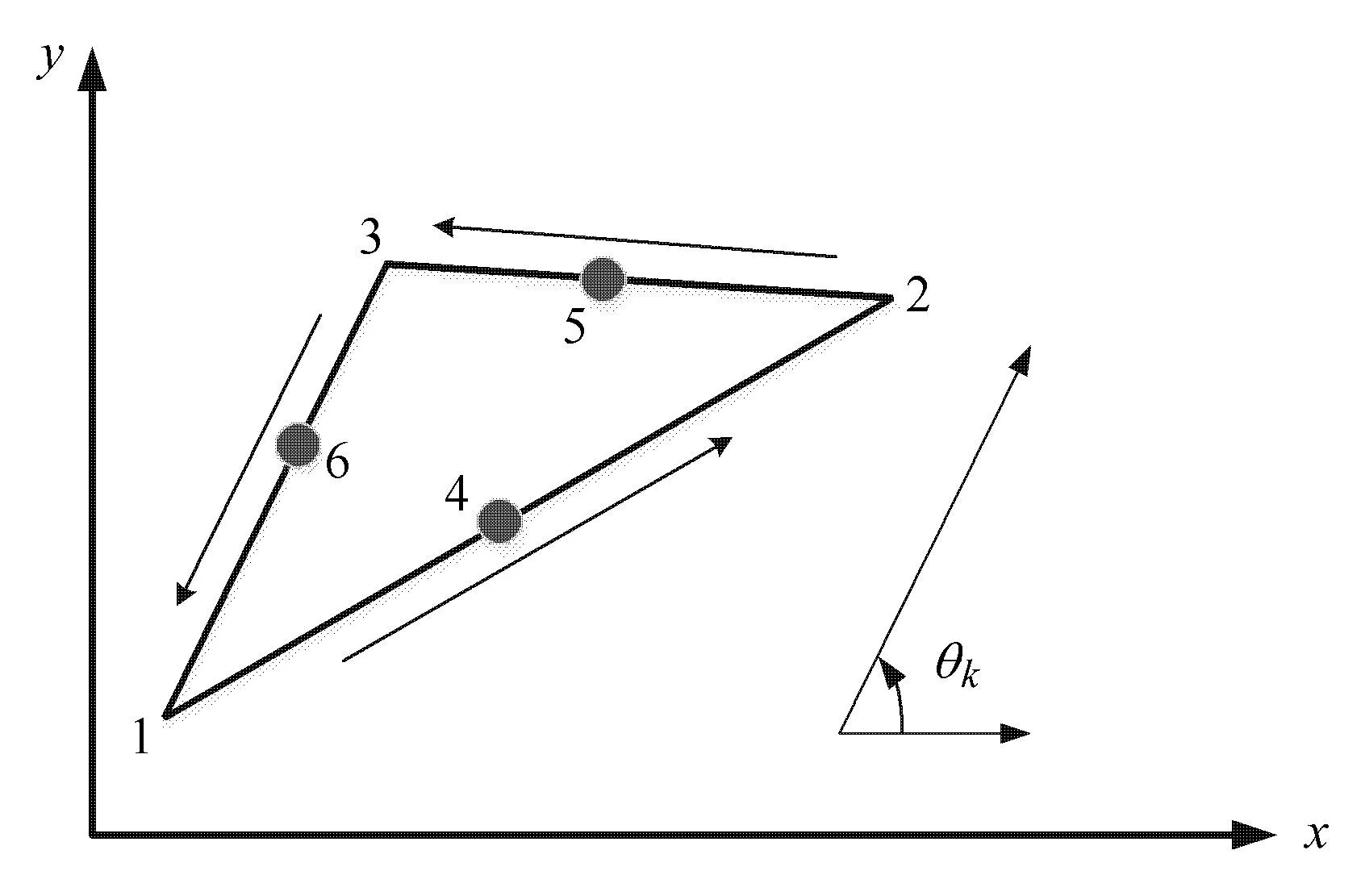
圖1 離散的Kirchho ff-M indlin三角形單元Fig.1 Discrete Kirchho ff-M indlin triangularelement

1.2 本構關系

彎曲應變為

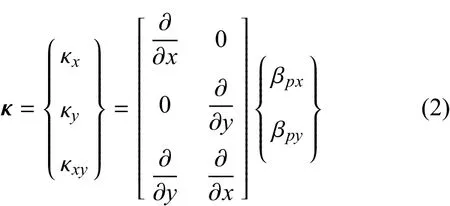
將式(1)代入式(2)，得

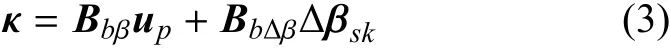
剪應變可以表示為

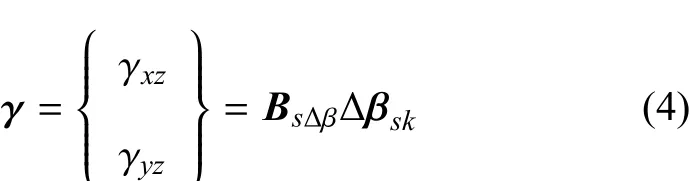
式中，up為三角形單元三個角節點位移，?βsk為三個邊中點切向轉角，?βsk與up之間有如下轉換關系

式(3)～式(5)中，Bbβ,Bb?β,Bs?β和An表達式見參考文獻[28].

對于線彈性、各向同性均勻的平板，彎矩本構方程為

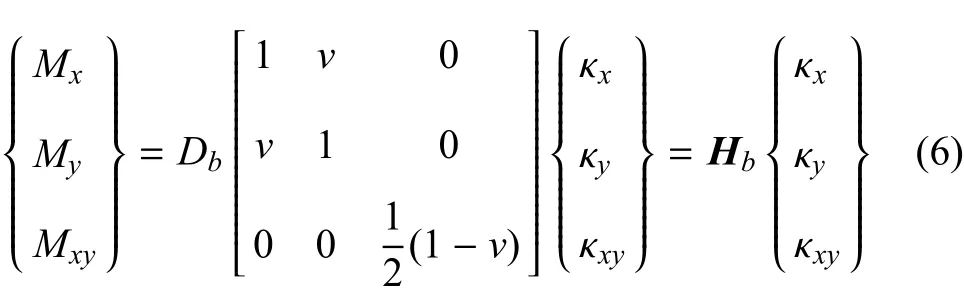
剪力本構方程為

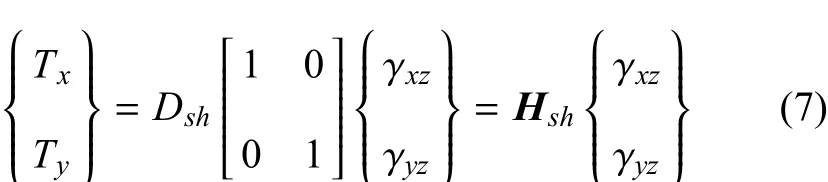
其中，Db=Eh3/12(1-v2)，Dsh=kGh，E是楊氏模量，h是平板厚度，v是泊松比，k=5/6是剪切修正系數，G是剪切模量.

1.3 單元的剛度矩陣與質量矩陣

彎曲剛度矩陣為

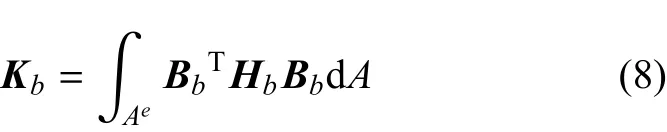
其中

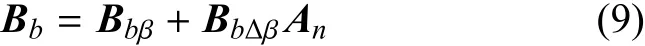
剪切剛度矩陣為

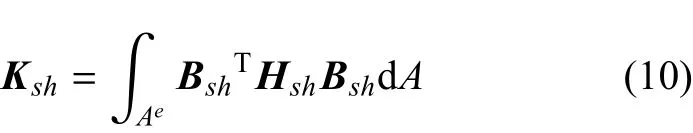
其中

則采用兩點高斯積分得到板單元的剛度矩陣為

單元的質量矩陣Mp采用集中質量矩陣，單元的每個結點上集中1/3的質量.

2 曲線加強筋理論

假設曲線加強筋具有均勻截面，由均質、各向同性、線彈性材料制成，如圖2所示.利用三節點等參梁單元模擬加強筋，其坐標可由節點坐標和插值函數表示為

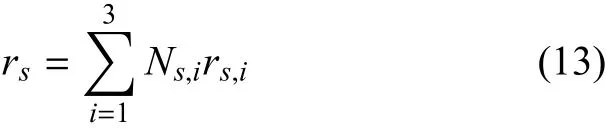
加強筋的彈性常數矩陣可以寫為

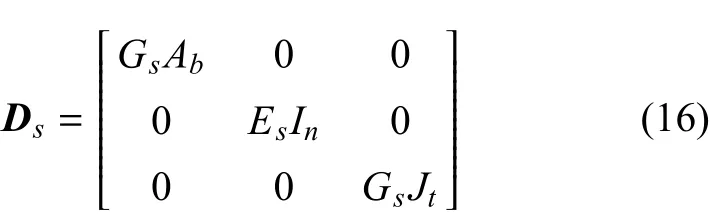
其中，rs=(xs,ys)為加強筋在整體坐標系中的坐標；Ns,i是3節點等參曲梁單元的形函數.根據曲線筋的切線方向t、法線方向n、次法線方向b建立局部坐標系,任意點的位移場可由其單元節點位移和插值函數表示為

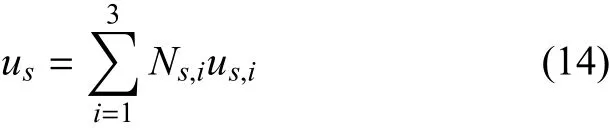
加強筋的質量矩陣可以寫成

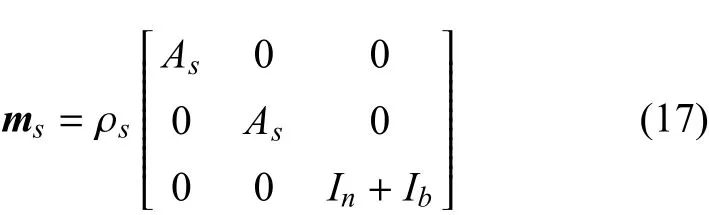
其中，usT={wb,βt,βn},us,i是局部坐標系下曲線筋單元第i個節點的位移.

線性應變可以表示為

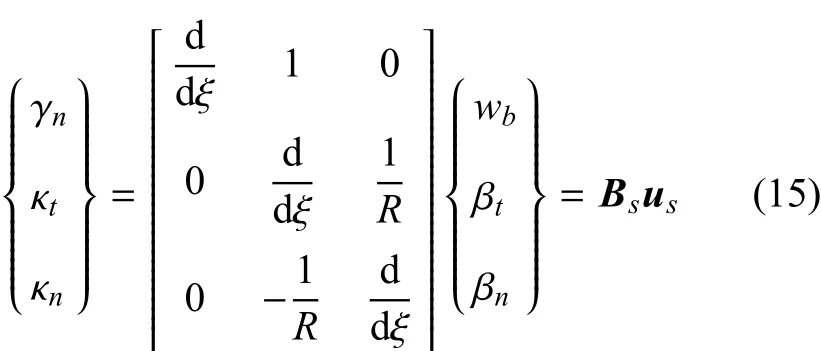
其中,1/R表示加強筋曲率[14],Es是加強筋的彈性模量；Gs是加強筋的剪切模量；A是加強筋的橫截面積；bs和hs分別是加強筋的截面寬度和高度；Ab表示b方向的剪切面積,Ab=KbA；Kb表示b方向的剪切強度因子；In和Ib表示加強筋橫截面相應于n方向和b方向的二次轉矩，In=bs/12+e2As，Ib=bs/12；Jt是加強筋截面的扭力常數，對于矩形加強筋，可以近似表示為Jt=hs/3.

3 加筋板有限元方程

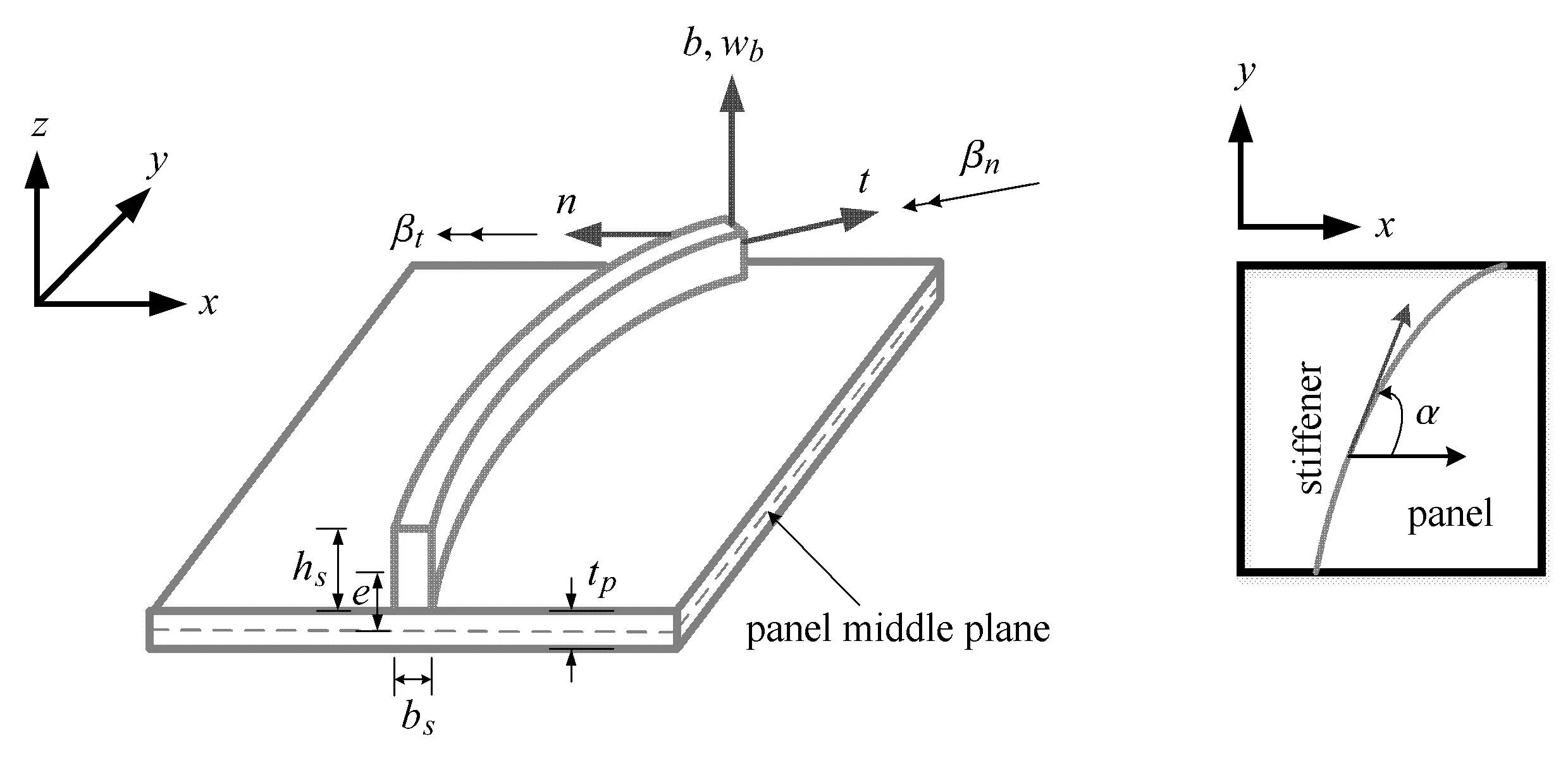
圖2 加強筋位移和局部坐標系Fig.2 Displacementand localcoordinate system for the curved sti ff eners

得到上述加強筋應變矩陣及彈性矩陣后，可通過數值積分計算加強筋剛度矩陣和質量矩陣，但此時的剛度矩陣和質量矩陣仍由加強筋的位移來表示，為建立加筋板的有限元方程，需采用板的節點位移來表示加強筋的位移.分析流程如圖3所示.

在筋板接觸位置，筋與板的坐標和位移都應是相同的，板單元內的坐標和位移可采用板單元節點插值表示，在整體坐標系下，第i個筋節點的坐標可由板節點坐標表示為

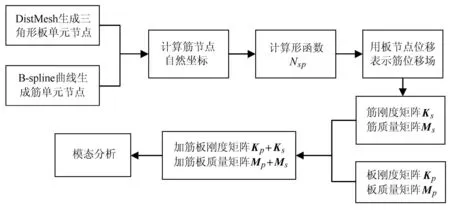
圖3 曲線加筋板模態分析流程Fig.3 Flow chartofmodalanalysis for curvilinearly sti ff ened plates

加強筋在局部坐標系下和整體坐標系下的位移可以通過轉換矩陣實現轉換

其中，usgT={ws,βsx,βsy}為加強筋在整體坐標系下的位移.轉換矩陣為

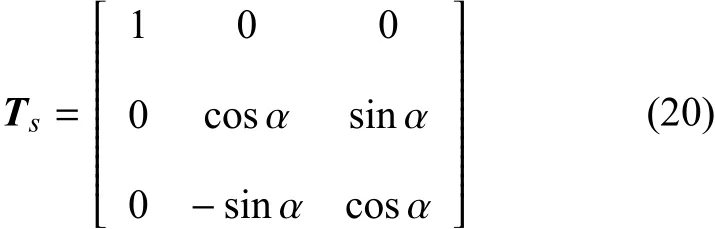
加強筋在整體坐標系下的位移可用筋節點位移插值表示為

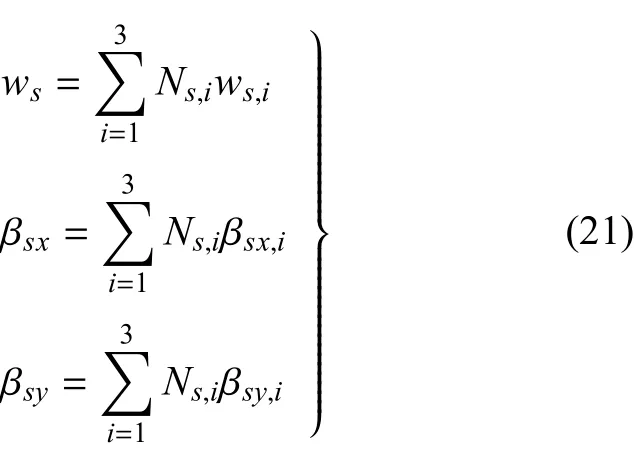
則整體坐標系下第i個筋節點的位移可由板節點位移表示為

根據式(5)可知邊中點切向轉角與板三個角節點位移之間的關系，將式(5)和式(22)代入式(21)可得

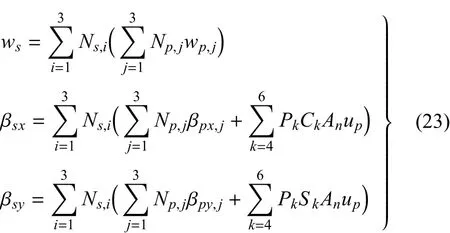
則加強筋內的位移場就可由板單元的節點位移來表示

至此，筋和板節點位移自由度轉化完成，并可以得到由板的位移自由度表示的加強筋的剛度矩陣，則加強筋的單元剛度矩陣可以表示為

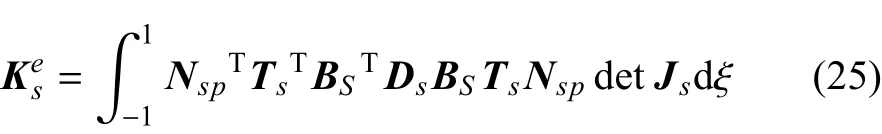
加強筋的單元質量矩陣可以表示為

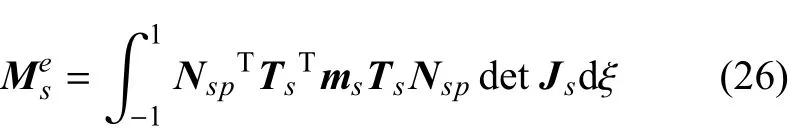
Js是筋單元的雅克比矩陣,行列式的值為

建立曲線加筋板的自由振動分析有限元方程如下

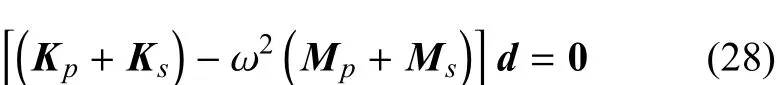
其中,Kp和Ks分別是板和筋的剛度矩陣，通過兩點高斯積分求得；Mp和Ms分別是板和筋的質量矩陣，Mp由集中質量矩陣求得，Ms通過兩點高斯積分求得；ω是固有頻率；d是板的節點位移自由度向量.

4 曲線筋參數化建模

Zhao等[10]提出一種曲線筋參數化建模方法，在參數化空間中，曲線筋的位置、曲率和筋條數目用于參數化加強筋的形狀.利用三階B-Spline曲線來生成曲線筋的形狀曲線，起始點A和結束點B位于自然空間上的邊緣，用于參數化曲線筋的位置，控制點C用來控制曲線筋的曲率.初始控制點C0是線段AB中點，d是垂直于向量AB的單位向量，控制點C的位置可以按曲率設計步長α沿方向d移動C0得到.曲線加強筋的參數化表達方式如圖4所示.邊界參數與點自然坐標的關系如表1所示.

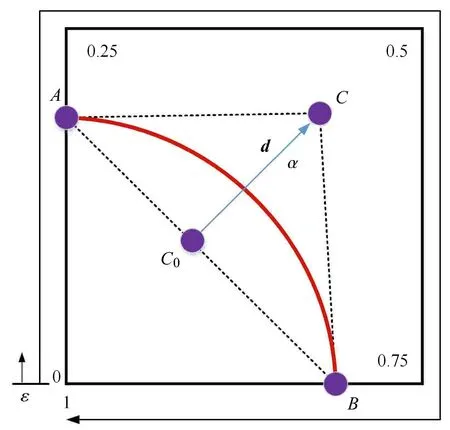
圖4 曲線加強筋的參數化表達方式Fig.4 Parametric expression of curvilinear sti ff ener

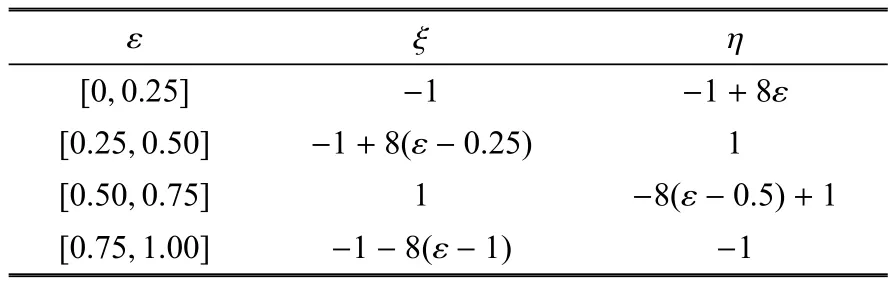
表1 邊界參數c和點自坐標(ξ,η)的關系Table1 The relationship between the perimeterparameterε and the pointnatural coordinates(ξ,η)

5 數值算例

5.1 直線加筋板自由振動分析

考慮一四周固支的直線加筋板，如圖5所示，加強筋偏心布置，材料參數E=68.9GPa，v=0.3，ρ=2670 kg/m3，進行自由振動分析.Olson等[31]對此模型進行了自由振動實驗以及有限元分析，Holopainen[23]應用一種混合插值彎曲板單元對此模型進行自由振動分析，Nguyen-Thoi等[24]基于平滑離散剪切間隙方法，將板單元和膜元結合，并使用厚梁單元模擬筋條對此模型進行了自由振動分析.

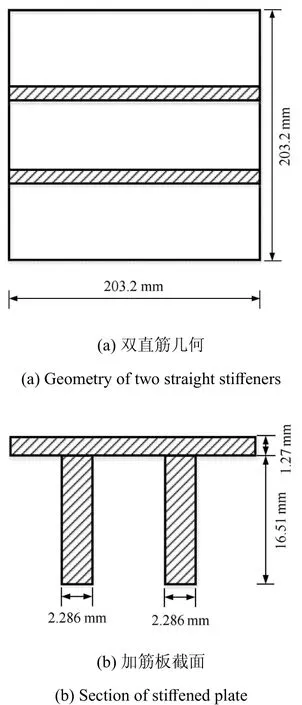
圖5 雙筋直線加筋板幾何模型Fig.5 Geometry of sti ff ened platew ith two straightsti ff eners

首先進行收斂性研究，計算無筋板固有頻率隨網格密度變化，從表2結果可知,當板網格密度為32×32時，板的自由振動頻率開始收斂.保持板網格密度為32×32，研究直線加筋板固有頻率隨筋單元數目變化的收斂性，直線加筋板固有頻率結果如表3所示.由表3可知，當筋單元數目為15時，加筋板固有頻率開始收斂.由此可見，板單元網格密度采用32×32，每條加強筋單元數目采用15時，對此模型進行自由振動分析結果是收斂的.

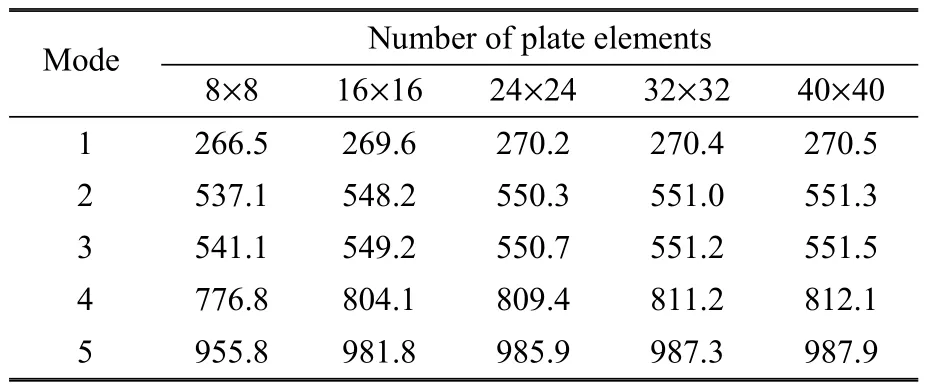
表2 無筋板固有頻率隨網格密度變化Table 2 Natural frequencies change foran unsti ff ened plate w ith the panelmesh densityHz

表3 不同筋單元數目下加筋板(32×32)固有頻率Table 3 Natural frequencies change for the sti ff ened plate(32×32)w ith di ff erentsti ff enerelementsnumber Hz

為了驗證本方法的準確性，將本文計算所得數值結果與參考文獻[23-24,31]中的試驗及仿真結果進行對比.對比結果參見表4和圖6.由對比結果可知，本方法求得的固有頻率和文獻結果吻合較好，本方法的精確性得到了驗證.

5.2 曲線加筋板自由振動分析

5.2.1 收斂性及準確性驗證

考慮一中心帶孔曲線加筋板，模型如圖7所示，材料參數E=69GPa，v=0.3，ρ=2823 kg/m3，曲線筋的位置和曲率參數分別為?ε=0.0625，α=0.5,方板邊長a=2m，厚度為t，孔半徑為r=0.4m，曲線筋截面如圖2所示，采用偏心加強筋，截面高度hs=0.1908m，寬度bs=0.0191m.邊界條件為四周簡支.

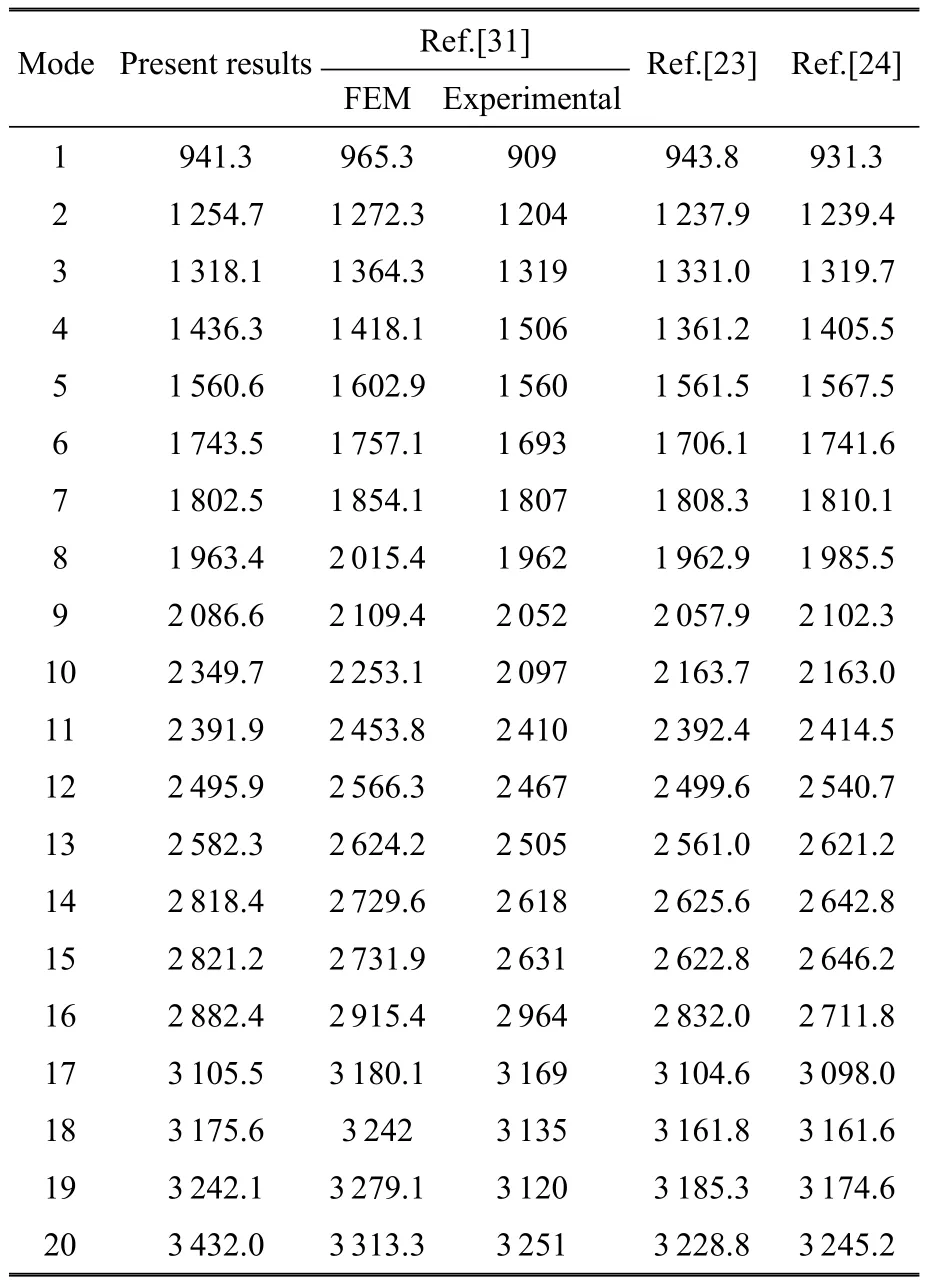
表4 直線加筋板固有頻率Table 4 Natural frequenciesof the linearly sti ff ened plate Hz

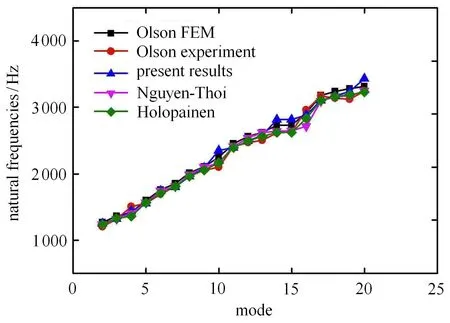
圖6 直線加筋板固有頻率對比Fig.6 Comparison ofnatural frequencies for the linearly sti ff ened plate

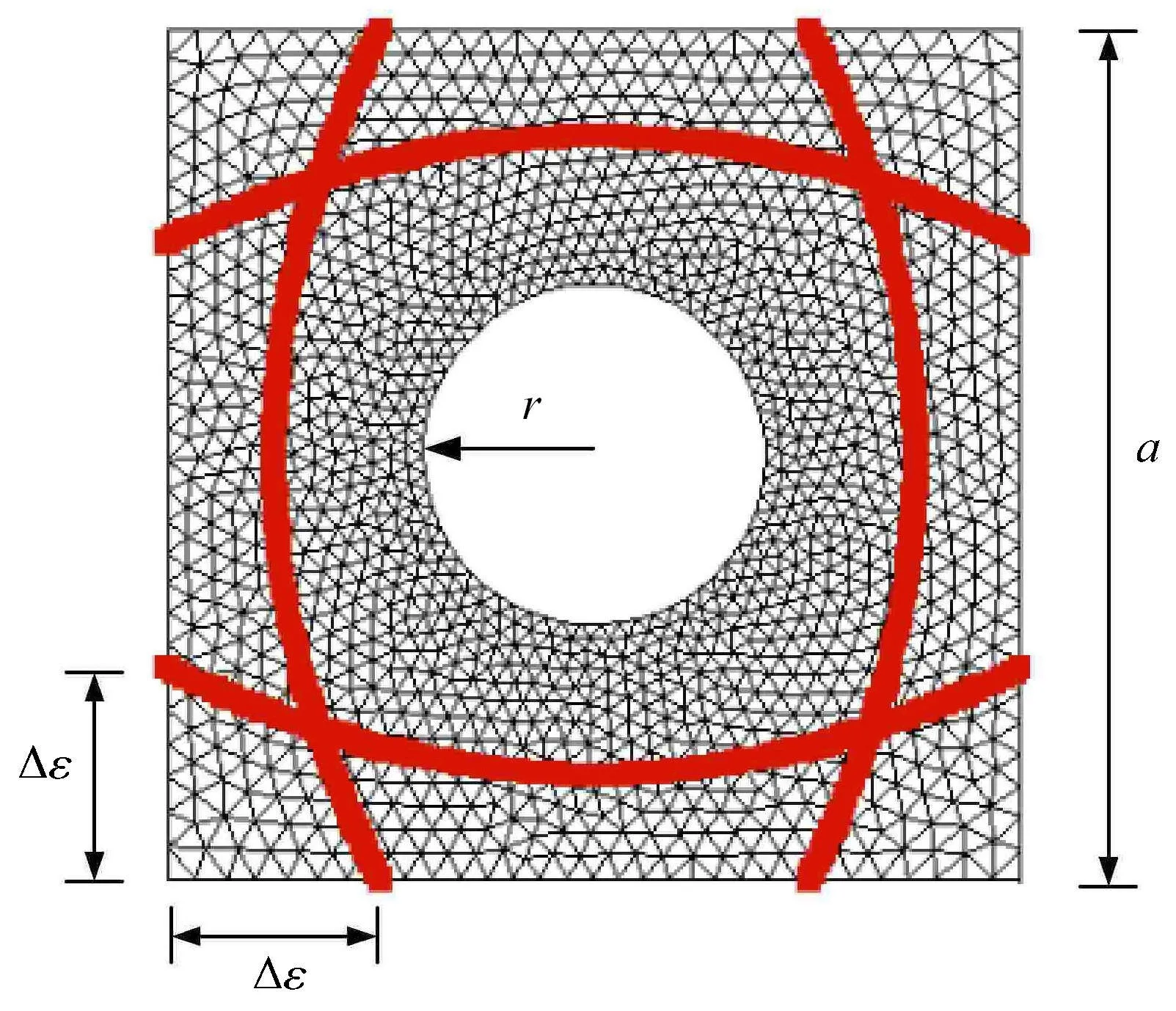
圖7 曲線加筋板有限元模型Fig.7 Finiteelementmodel for the curvilinearly sti ff ened plate

使用網格劃分工具DistMesh劃分板有限元網格，選擇固定網格密度函數，通過調節參數h0來控制板單元網格劃分[30].使用三階B-Spline曲線來生成曲線筋的形狀曲線，為保證筋條交匯處位移協調，在筋條交匯處建立節點，如圖8所示.

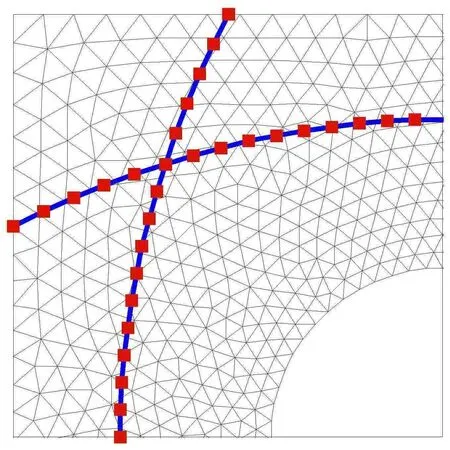
圖8 筋條交匯處有限元模型Fig.8 Finiteelementmodelof intersection of sti ff eners

首先進行收斂性驗證，選擇板厚t=0.02m，通過調節參數h0獲得5種不同密度網格，如圖9所示.對不加筋板進行自由振動分析，5種不同密度板單元網格下板的固有頻率結果如表5所示.結果表明，當h0=0.04時，板的固有頻率開始收斂.保持板單元網格為h0=0.04時不變，網格數為2469，考察了不同數目筋單元對曲線加筋板的頻率結果的影響.

圖9 板單元網格劃分Fig.9 Di ff erentmesh size for the plate

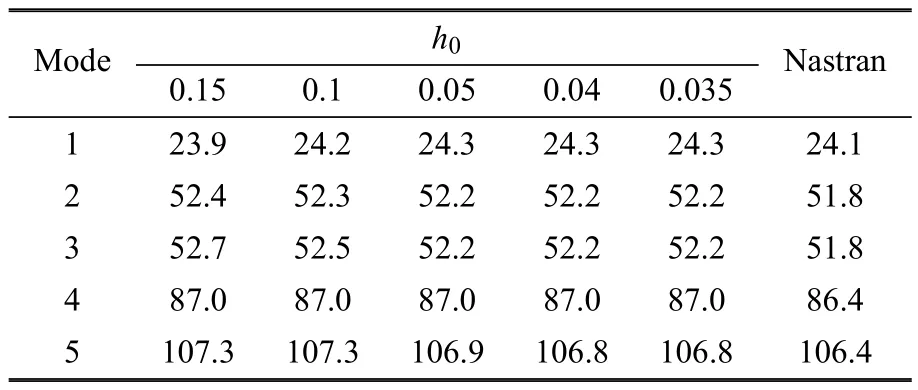
表5 無筋帶孔板固有頻率隨板的網格尺寸變化(t=0.02m)Table 5 Natural frequencies change foran unsti ff ened plate w ith aholew ith the panelmesh size(t=0.02m)Hz

曲線加筋板固有頻率隨著每條筋單元數目變化結果如表6和圖10所示.結果表明，當每條筋采用15個單元時，曲線加筋板頻率結果開始收斂，因此采用h0=0.04時的板網格和每條筋15個三節點梁單元作為本例的有限元模型，其數值結果認為是本方法的可靠結果.

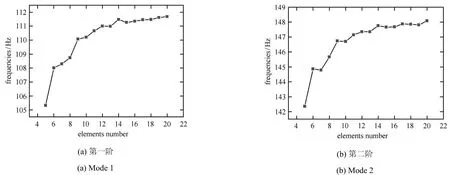
圖10 曲線加筋板固有頻率隨每條筋單元數目變化Fig.10 Natural frequencies change for the curvilinearly sti ff ened platew ith di ff erentsti ff ener elementsnumber

為驗證本方法的準確性，將數值結果與Nastran結果進行對比，結果如表6所示.在Nastran建模中，采用6243個CTRIA3板單元，每條曲線加強筋采用50個CBAR梁單元.對比結果顯示誤差較小，本文方法準確性得到了驗證.

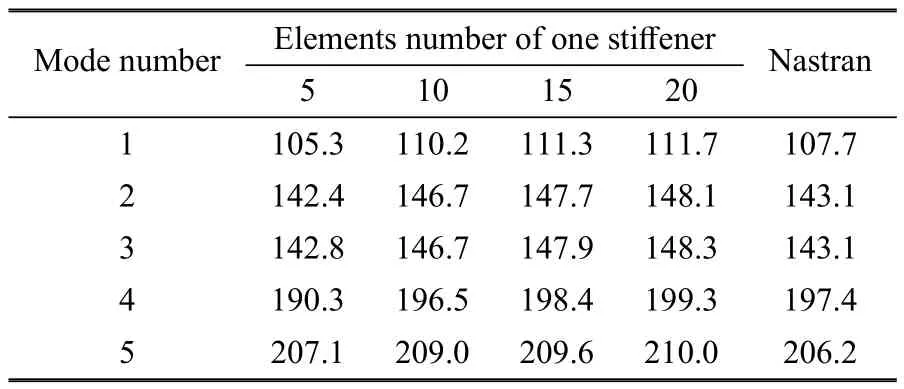
表6 曲線加筋板固有頻率隨筋單元數目變化(t=0.02m)Table 6 Natural frequencieschange for the curvilinearly sti ff ened platew ith the sti ff enerelementsnumber(t=0.02m)Hz

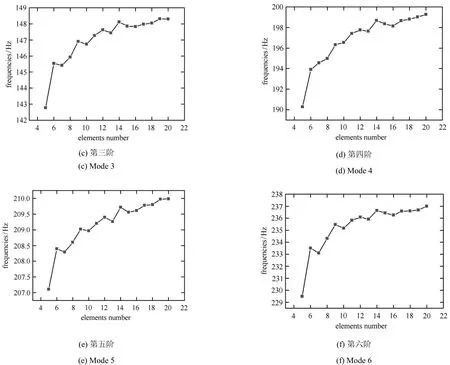
圖10 曲線加筋板固有頻率隨每條筋單元數目變化(續)Fig.10 Natural frequencieschange for the curvilinearly sti ff ened platew ith di ff erentsti ff enerelementsnumber(continued)

5.2.2 振型分析結果

除了固有頻率的驗證，振型的驗證也是必要的，振型的精確與否可以反映本文方法所求特征向量的準確性.利用圖7模型，選擇t=0.02m和t=0.2m兩種板厚，兩種情況下的前五階振型及頻率分別如圖11和圖12所示.從圖11和圖12可以看出,本文方法所獲得振型及頻率與Nastran結果吻合較好.

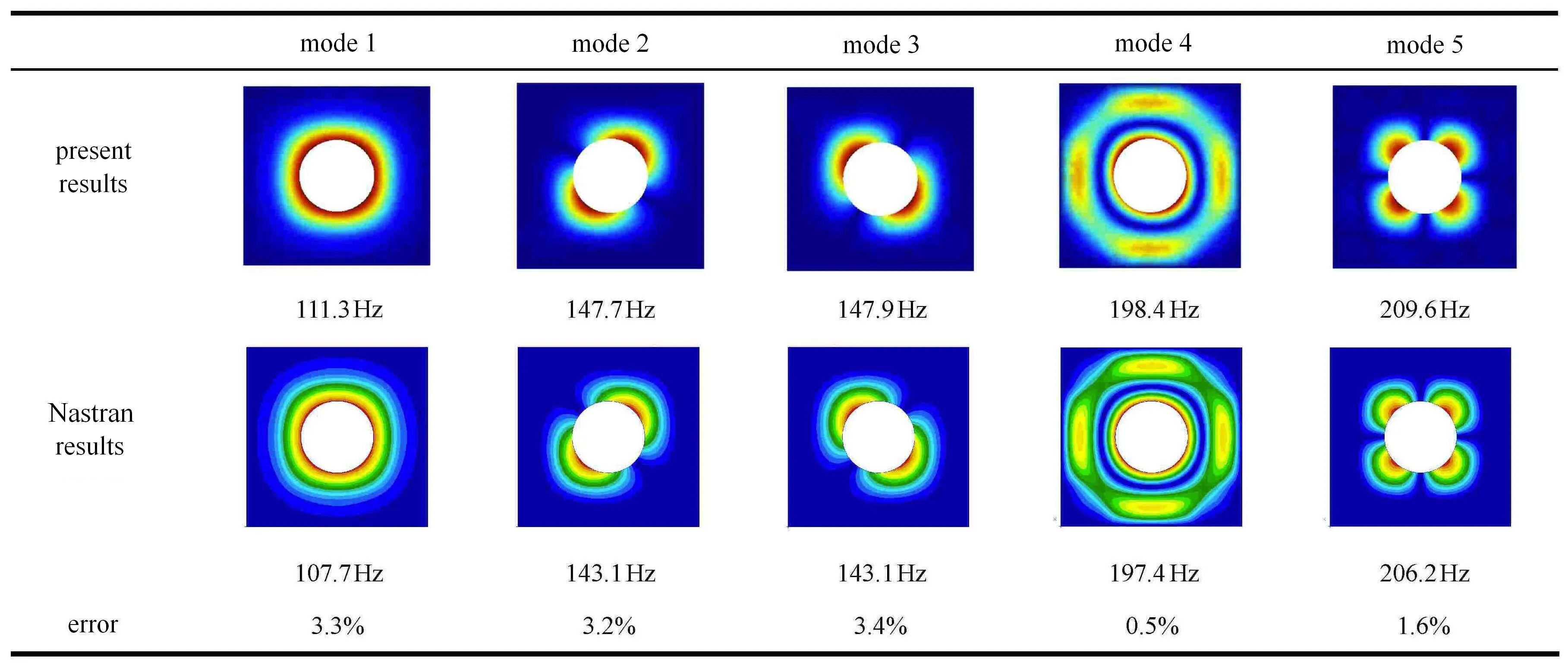
圖11 曲線加筋板振型(t=0.02m)Fig.11 Mode shapesof the curvilinearly sti ff ened plate(t=0.02m)

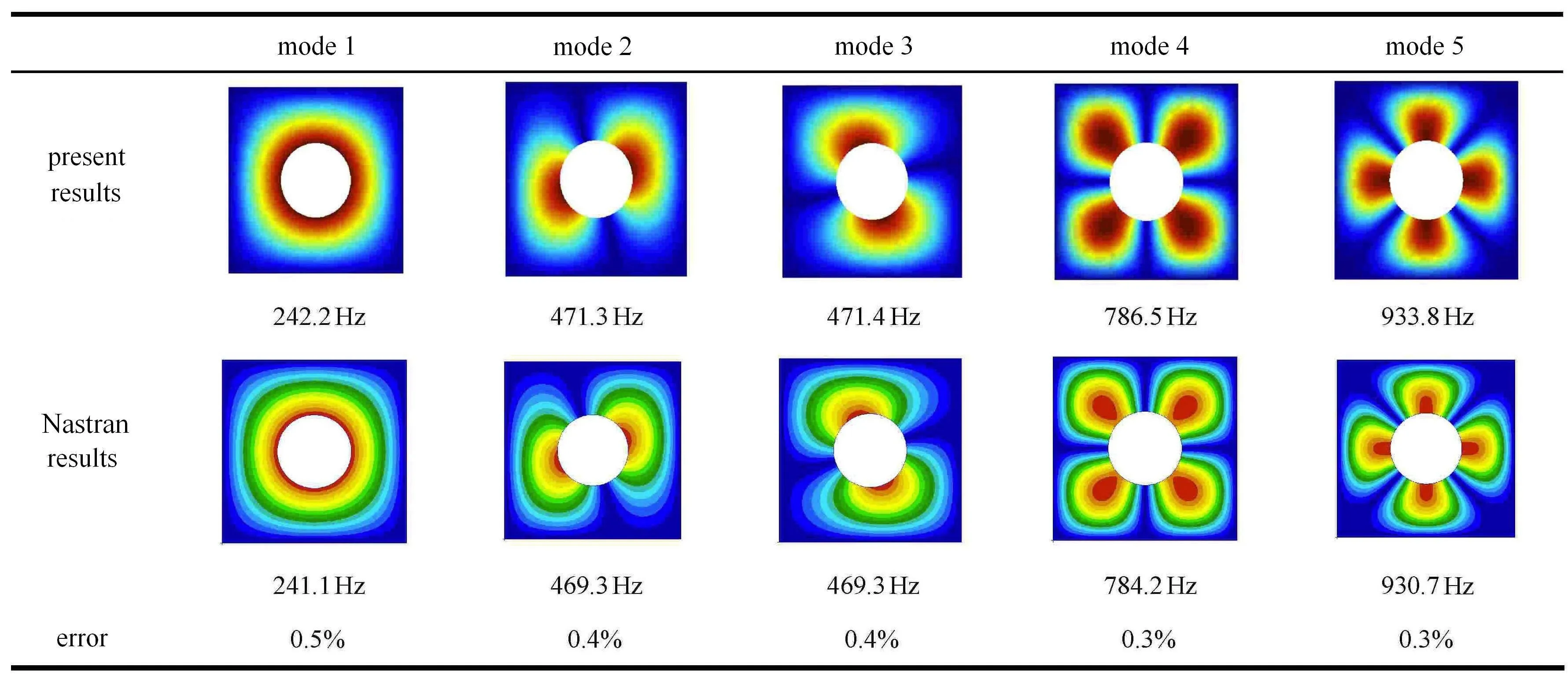
圖12 曲線加筋板振型(t=0.2m)Fig.12 Mode shapesof the curvilinearly sti ff ened plate(t=0.2m)

6 結論

本文以離散的Kirchho ff-M indlin三角形單元為板單元，Timoshenko梁單元為筋單元，建立了直線與曲線加筋板有限元模型，分別對雙直筋加筋板與4條加強筋曲線加筋板進行模態分析，將計算結果與文獻及Nastran仿真結果進行對比分析.得到如下結論：

(1)采用離散的Kirchho ff-M indlin三角形單元和Timoshenko梁單元分別為加筋板的板單元和梁單元，實現了一種曲線加筋板有限元分析方法.筋板單元無需共節點，當加強筋單元發生改變時，板網格無需進行改變.有限元分析結果表明,本文方法可同時適用于薄板和厚板情況下的曲線加筋板分析.

(2)通過收斂性研究表明,本文方法對于分析直線和曲線加筋板問題收斂性較好.通過與文獻結果及Nastran結果對比表明,本文方法所得固有頻率及特征向量精度較高，且本文方法可以采用比商業有限元軟件更少的網格獲得精度相近的結果.

(3)采用離散的Kirchho ff-M indin三角形單元模擬板單元進行加筋板分析時，板單元內撓度場可以通過單元角點撓度線性插值來表示，筋的位移自由度可以通過板的位移插值函數及筋板交界面的位移兼容條件，與板的位移自由度建立起映射關系，進而建立起基于板的位移自由度的結構有限元方程.

(4)可以通過改變曲線筋的數目、位置和曲率參數來得到不同的曲線加筋板模型進行分析，從而對曲線加筋板結構的力學性能進行改變，為曲線加筋板結構優化設計提供了基礎.

1 Kapania RK,Li J,Kapoor H.Optimal design of unitized panels w ith curvilinear sti ff eners//AIAA 5th ATIO and the AIAA 16th Lighter-than-Air Systems Technology Conferenceand Balloon SystemsConference,2005,3：1708-1737

2 Mukherjee A,Mukhopadhyay M.Finite element free vibration of eccentrically sti ff ened plates.Computers&Structures,1988,30(6)：1303-1317

3 Biswal KC,Ghosh AK.Finite element analysis for sti ff ened lam inated platesusing higherordersheardeformation theory.Computers&Structures,1994,53(1)：161-171

4 Ghosh AK,Biswal KC.Free-vibration analysis of sti ff ened laminated platesusing higher-order shear deformation theory.Finite Elements in Analysisand Design,1996,22(2)：143-161

5 Kumar YVS,Mukhopadhyay M.A new triangularsti ff ened plateelement for laminate analysis.Composites Science and Technology,2000,60(6)：935-943

6 Kumar YVS,Srivastava A.First ply failure analysis of lam inated sti ff ened plates.Composite Structures,2003,60(3)：307-315

7 Peng S,Kapania RK,Dong CY.Finite Element Approach to the Static,Vibration and Buckling Analysis of Curvilinearly Sti ff ened Plates//56th AIAA/ASCE/AHS/ASC Structures,StructuralDynamics,and MaterialsConference,2015

8 Kumar YVS,Mukhopadhyay M.A new finit element for buckling analysis of lam inated sti ff ened plates.Composite Structures,1999,46(4)：321-331

9 Shi P,Kapania RK,Dong CY.Vibration and buckling analysis of curvilinearly sti ff ened plates using finit elementmethod.AIAA Journal,2015,53(5)：1319-1335

10 Zhao W,Kapania RK.Buckling analysis of unitized curvilinearly sti ff ened composite panels.Composite Structures,2016,135：365-382

11 Prusty BG,Satsangi SK.Analysis of sti ff ened shell for ships and ocean structures by finit elementmethod.Ocean Engineering,2001,28(6)：621-638

12 Prusty BG,Satsangi SK.Finite element transient dynam ic analysisof lam inated sti ff ened shells.JournalofSound and Vibration,2001,248(2)：215-233

13 KumarYVS,Mukhopadhyay M.Transientresponseanalysisof laminated sti ff ened plates.Composite Structures,2002,58(1)：97-107

14 ZhaoW,Kapania RK.Vibration analysis of curvilinearly sti ff ened composite panel subjected to in-plane loads.AIAA Journal,2017,55(3)：981-997

15 Shi P,Kapania RK,Dong CY.Free vibration of curvilinearly sti ffened shallow shells.Journal of Vibration and Acoustics,2015,137(3)：031006

16 M iller RE.Dynamic aspects of the error in eccentric beam modelling.International Journal for Numerical Methods in Engineering,1980,15(10)：1447-1455

17 M iller RE.Reduction of the error in eccentric beam modelling.International Journal for Numerical Methods in Engineering,1980,15(4)：575-582

18 Rikards R,Chate A,Ozolinsh O.Analysis for buckling and vibrationsof compositesti ff ened shellsand plates.Composite Structures,2001,51(4)：361-370

19 Bhar A,Phoenix SS,Satsangi SK.Finite elementanalysis of lam inated compositesti ff ened platesusing FSDT and HSDT：A comparative perspective.Composite Structures,2010,92(2)：312-321

20 Thinh TI,Quoc TH.Finite element modeling and experimental study on bending and vibration of laminated sti ff ened glass fibe/polyester composite plates.ComputationalMaterials Science,2010,49(4)：S383-S389

21 Barik M,Mukhopadhyay M.A new sti ff ened plate element for the analysis of arbitrary plates.Thin-Walled Structures,2002,40(7)：625-639

22 Mukhopadhyay M,Mukherjee A.Finite elementbuckling analysis of sti ff ened plates.Computers&Structures,1990,34(6)：795-803

23 Holopainen TP.Finite element free vibration analysis of eccentrically sti ff ened plates.Computers&Structures,1995,56(6)：993-1007

24 Nguyen-Thoi T,Bui-Xuan T,Phung-Van P,et al.Static,free vibration and buckling analysesof sti ff ened platesby CS-FEM-DSG3 using triangularelements.Computers&Structures,2013,125：100-113

25章向明,王安穩.復合材料大變形任意加筋板單元.工程力學,2001,18(3)：131-135(Zhang Xiangm ing,Wang Anwen.Geometrically nonlinearplateelement forarbitrarily sti ff ened laminated composite plates.Engineering Mechanics,2001,18(3)：131-135(in Chinese))

26章向明,王安穩,梅炎祥.復合材料大變形任意加筋殼單元.工程力學,2003,20(5)：134-138(Zhang Xiangm ing,Wang Anwen,Mei Yanxiang.A large deformation shell element for eccentrically arbitrary sti ff ened composite shells.Engineering Mechanics,2003,20(5)：134-138(in Chinese))

27張志峰,陳浩然,白瑞祥.一種分析AGS結構的三角形加筋板殼單元.工程力學,2006,23(A01)：203-208(Zhang Zhifeng,Chen Haoran,Bai Ruixiang.A new triangular sti ff ened plate/shell element for compositegrid structureanalysis.Engineering Mechanics,2006,23(A01)：203-208(in Chinese))

28 Katili I.A new discrete Kirchho ff-M indlin element based on M indlin-Reissner plate theory and assumed shear strain fields—par I：An extended DKT element for thick-plate bending analysis.International Journal for Numerical Methods in Engineering,1993,36(11)：1859-1883

29 Persson PO,Strang G.A simplemesh generator in MATLAB.SIAM Review,2004,46(2)：329-345

30 Katili I,Maknun IJ,HamdouniA,etal.Application of DKMQ element for composite plate bending structures.Composite Structures,2015,132：166-174

31 Olson MD,Hazell CR.Vibration studies on some integral ribsti ff ened plates.JournalofSound and Vibration,1977,50(1)：43-61

FREE VIBRATION ANALYSISOFCURVILINEARLY STIFFENED KIRCHHOFF-M INDLIN PLATES1)

Liu Jingze?,?Jiang Dong?,??Han Xiaolin?FeiQingguo?,2)?(DepartmentofEngineering Mechanics，SoutheastUniversity，Nanjing 210096，China)?(Institute ofAerospace Machinery and Dynamics，SoutheastUniversity，Nanjing 211189，China)??(College ofMechanicaland Electronic Engineering，Nanjing Forestry University，Nanjing 210037，China)

Comparedw ith traditionalsti ff ened plates,curvilinearly sti ff ened plates can deliver themechanicalproperties ofmaterialsmoreadequately.Inmechanicalanalysisof sti ff ened thick plates,Reissner-M indlin theory isusually adopted.However,di ffi culties are encountered in connection w ith shear locking when the plate thickness approaches zero.In order to avoid the above problem,the discrete Kirchho ff-M indlin theory was investigated by employing the assumption of shear strain field An e ffi cient finit elementapproach for free vibration analysis of curvlinearly sti ff ened Kirchho ff-M indlin platesispresented in thispaper.ThediscreteKirchho ff-M indlin triangular(DKMT)elementand the Timoshenko curved beam element are employed formodeling the plate and the sti ff eners,respectively.The finit element equation is established through the displacement interpolation function of plate and the displacement compatibility conditions atthe plate-sti ff ener interfaces.In order to verify the e ffi ciency and accuracy of the presentmethod,linearly sti ff ened thin plateand curvilinearly sti ff ened thin and thick platesareused asnumericalexamples.The reasonable finit elementmesh density isselected by convergenceand accuracy analysis.The firs 20 natural frequenciesof the linearly sti ff ened plateare in good agreementw ith the literature.In the examplesof the curvilinearly sti ff ened plate,the number of plate elements satisfying the convergence condition is 2469,while the number in Nastranmodel is 6243.Themaximum error of the natural frequency between the presentmethod and Nastran is3.4%.Resultsshow thatpresentapproach can guarantee the accuracy of calculationw ith lessnumberofelements.Thepresentmethod can beapplied to the freevibration analysisof both sti ff ened thin and thick plates.

curvilinearly sti ff ener,Kirchho ff-M indlin plate,freevibration analysis

V214.3

A

10.6052/0459-1879-17-041

2017-02-16收稿，2017-05-27錄用,2017-06-01網絡版發表.

1)國家自然科學基金(11572086,11602112)及教育部新世紀優秀人才支持計劃(NCET-11-0086)資助項目.

2)費慶國，教授，主要研究方向：動力學與控制.E-mail：qgFei@seu.edu.cn

劉璟澤,姜東,韓曉林,費慶國.曲線加筋Kirchho ff-M indlin板自由振動分析.力學學報,2017,49(4)：929-939

Liu Jingze,Jiang Dong,Han Xiaolin,FeiQingguo.Free vibration analysisof curvilinearly sti ff ened Kirchho ff-M indlin plates.Chinese JournalofTheoreticaland Applied Mechanics,2017,49(4)：929-939