高超聲速飛行器磁控熱防護霍爾電場數值方法研究?

李開 柳軍 劉偉強

(國防科學技術大學航天科學與工程學院,長沙410073)

高超聲速飛行器磁控熱防護霍爾電場數值方法研究?

李開?柳軍 劉偉強

(國防科學技術大學航天科學與工程學院,長沙410073)

(2016年9月16日收到;2017年1月22日收到修改稿)

作為一種新概念高超聲速熱防護手段,磁控熱防護系統在實際應用中往往需要考慮霍爾效應的影響.為了在真實氣體環境下求解霍爾電場,采用交替隱式近似因子分解法建立并驗證了熱化學非平衡流體域電場數值求解方法.分析了電場虛擬步進因子和收斂性的關系以及影響步進因子取值的因素,提出了當地變步進因子加速電場收斂方法.研究表明,存在一個最優的步進因子ap使得霍爾電場收斂速度最快,并且隨網格尺度的減小和霍爾系數的增加,最優步進因子ap變大,電勢場收斂速率變慢.對于局部加密網格而言,當地變步進因子法的電勢收斂性明顯優于常規的定步進因子法.

磁流體控制,熱防護,霍爾效應,泊松方程

1 引言

熱防護系統是保護高超聲速飛行安全的關鍵子系統,一直以來都是高超聲速飛行器系統設計的關鍵一環[1].由于電磁流動控制技術近年來得到了飛速發展[2?4],作為其在高超聲速熱防護領域的一個應用,磁控熱防護技術顯示出了巨大的潛在應用價值,得到了各國科研機構的廣泛關注[5?7].

對于高超聲速飛行器前緣磁控熱防護而言,其核心在于在高超聲速飛行器鼻錐內部添加磁鐵,通過外加磁場和波后帶電流體的相互作用,感應產生洛倫茲力推出激波、減速流體、偏轉流線,從而降低到達壁面的熱流,實現熱防護.由于存在霍爾效應,磁場對電子的作用會使流動的法向和流向存在電勢差,即感應霍爾電場.根據通用歐姆定律,感應電場的存在會使得電流出現三維效應,進而改變洛倫茲力,影響磁控熱防護系統的效率.為分析霍爾效應對磁控熱防護系統的影響,必須耦合求解熱化學非平衡流場和霍爾電場.高超聲速條件下,由于波后電離度較低,低磁雷諾數假設往往可以得到滿足[8].此時,電磁場與非平衡流場的耦合計算可以通過求解電勢泊松方程和包含電磁源項的非平衡流動方程實現[9].流體域霍爾電場求解的關鍵在于求解電勢泊松方程.由于作為系數的電導率在激波位置存在間斷,并且在大霍爾系數條件下系數矩陣剛性問題嚴重[10],高超聲速流體域電勢泊松方程的求解存在魯棒性差、收斂性差等問題.Gaitonde等[11]和Wan等[12]分別基于有限差分法和有限體積法,采用虛擬時間步長以及近似因子分解-交替隱式方法實現了三維電勢泊松方程的數值離散與求解.Bisek[13]基于有限體積法采用連續超松弛算法(successive over-relaxation,SOR)完成了三維電勢泊松方程的迭代求解.呂浩宇等[14]、彭武等[15]同樣基于有限差分法采用超松弛算法求解了二維電勢泊松方程.Fujino等[16]采用基于Galerkin有限元素法求解二階半離散電勢泊松方程,與實驗結果符合良好.胡海洋等[10]采用無虛擬時間步的LUSGS預處理BI-CGSTAB算法解決了大霍爾系數下泊松方程病態矩的求解效率低的問題.綜上,目前見于文獻的霍爾電場求解方法主要有三種:1)超松弛迭代顯式算法;2)近似因子分解-交替隱式方法;3)有限元方法,如BI-CGSTAB,Galerkin方法等.相比而言,SOR算法為顯式算法,應用簡單且利于并行計算,但收斂效率低于隱式格式.有限元方法收斂性好,但在處理復雜壁面條件時存在困難.

目前關于霍爾電場的研究往往僅限于Poisson方程求解方法的構建,對霍爾電場收斂性的研究較少.針對霍爾電場收斂性和步進因子ap的關系,Wan等[12]給出了其建議取值范圍0.001—0.01;Gaitonde[11]則采用了Holst[17]提出的步進因子根據其上下限隨時間步過渡變化的指數公式.但是,Wan給出的范圍只針對其所采用的網格,不具有普適性.Holst的方法也必須首先確定步進因子的上下限,實際操作困難.因此,本文首先構造三維霍爾電場的隱式數值方法,而后進行霍爾電場收斂性的影響因素研究,以便為高超聲速飛行器前緣磁控熱防護系統的電磁場流場耦合計算分析提供參考.

2 數學模型

2.1 控制方程

高超聲速飛行器定常繞流條件下,由于波后等離子體電離度往往低于1×10?4[18,19],此時,低磁雷諾數假設通常可以得到滿足,并且外加穩定磁場時,磁場和感應電場的變化通常都可以忽略不計.因此,可以對安培-麥克斯韋公式、法拉第定律進行簡化,將對感應場強矢量E以及感應電流密度J的求解轉化為對標量電勢?的求解,結合廣義歐姆定律

可以得到關于?的電勢泊松方程

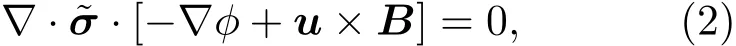
其中u為流體速度矢量,B為磁感應強度矢量,電導率張量?σ可以由下式求出:

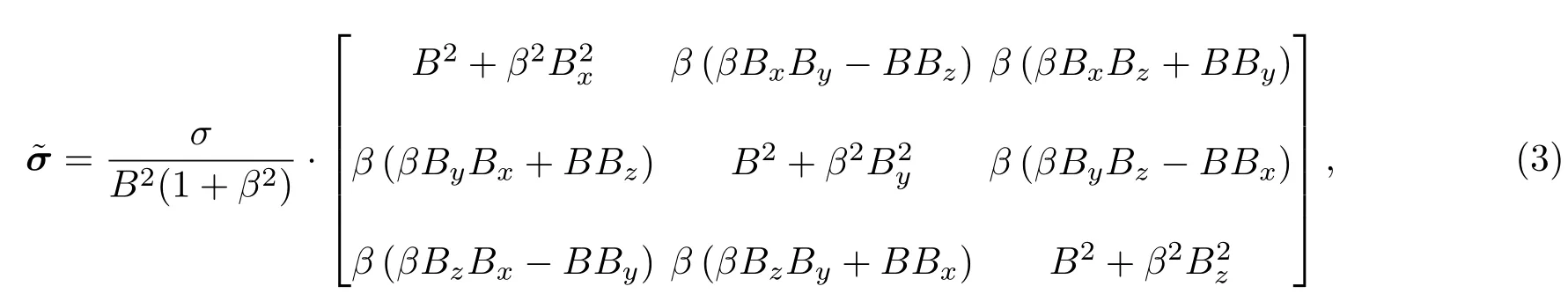
其中,β為霍爾系數,并且為分析霍爾系數對步進因子取值、電場計算收斂性的影響,采用均布霍爾系數模型.σ為標量電導率,采用Fujino電導率模型計算[16]:

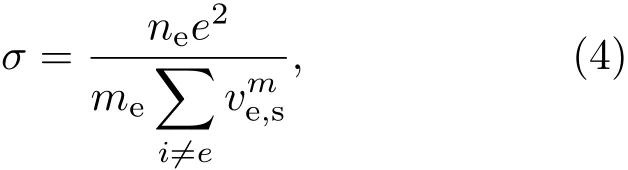
其中,e,ne,Me分別為電子電量、電子數密度、電子質量.為電子和其他組元的有效動量傳輸碰撞頻率[20].

2.2 數值方法

由于電導率σ在激波處存在間斷,作為系數的電導率張量在激波處也同樣存在間斷,這使得上述電勢泊松方程(2)在求解時穩定性差.特別是在大霍爾系數條件下,系數矩陣很有可能會出現對角不占優的情況,使得方程剛性嚴重,影響迭代計算的收斂性.為此,我們采用能有效抑制剛性的近似因子分解-交替隱式方法.并且為了保證三維多分區網格在數值離散中的幾何守恒性,將基于單元中心有限體積法對上述泊松方程進行離散.過程如下.

對于特定體積V,(1)式可以化為

將(6)式中右側展開,可得到

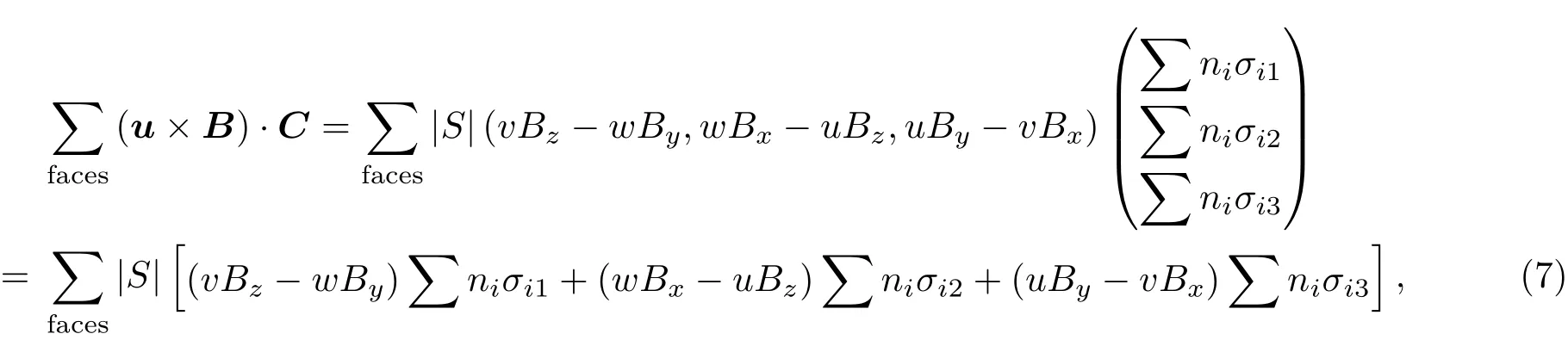
其中|S|和(n1,n2,n3)分別是單元面的面積及法向矢量.令

(i=1,2,3).則有

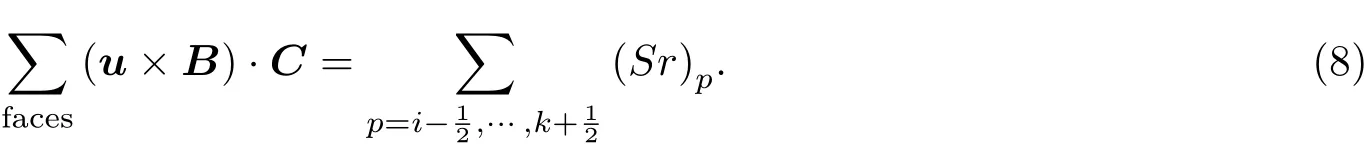
對??在三個計算坐標方向做分解并應用鏈式法則,則有

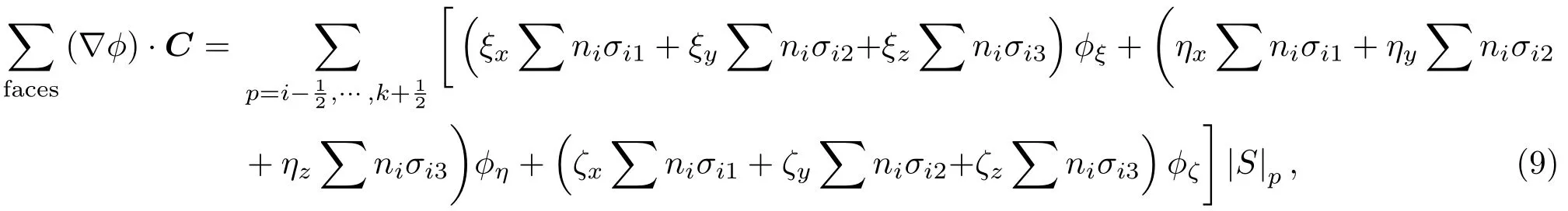
其中,ξ,η,ζ分別是i,j,k三方向的坐標變換系數.令XIC,ETC,ZTC如(10)式所示:

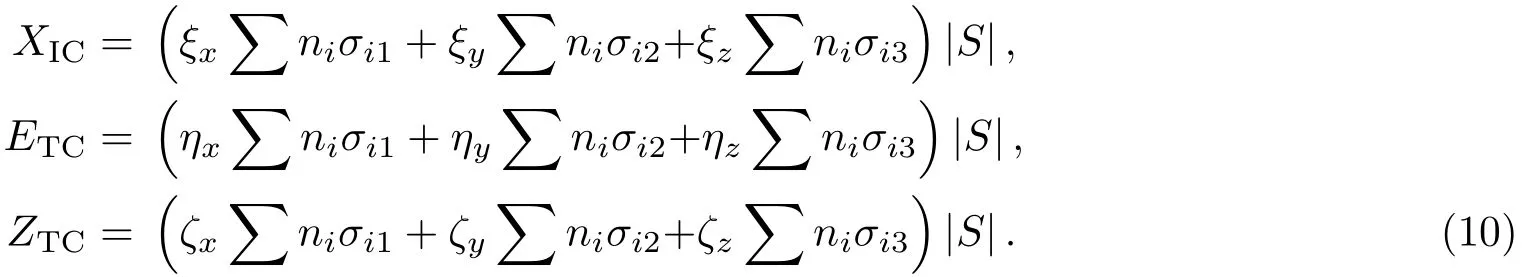
采用虛擬時間推進法進行迭代求解,則(6)式可以化為

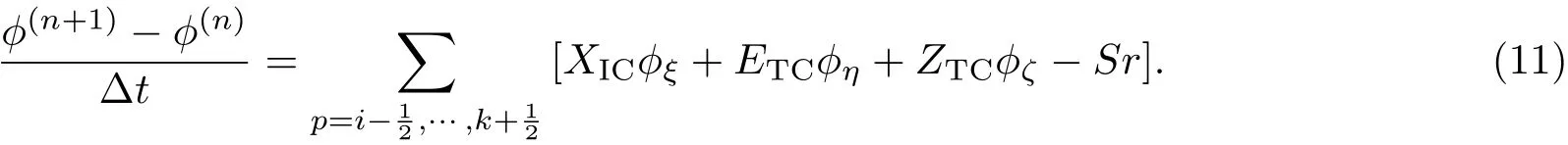
應用中心差分對(6)式進行離散,得到(i,j,k)及其周圍十八點的差分表達式.對于?i,j,k及臨近的六個點?i+1,j,k,?i?1,j,k,?i,j+1,k,?i,j?1,k,?i,j,k+1,?i,j,k?1進行隱式處理?(n+1)=?(n)+??(n),并令

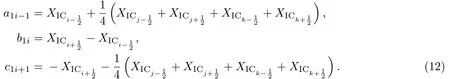
a2j?1,b2j,c2j+1,a3k?1,b3k,c3k+1形式類似,不再贅述.令步進因子ap=1/?t,則(11)式可以化為

令(13)式中右端項為RE,左端項采用交替隱式-近似因子分解法(ADI-AF),并定義算子Ai,Bj,Ck如(14)式所示:

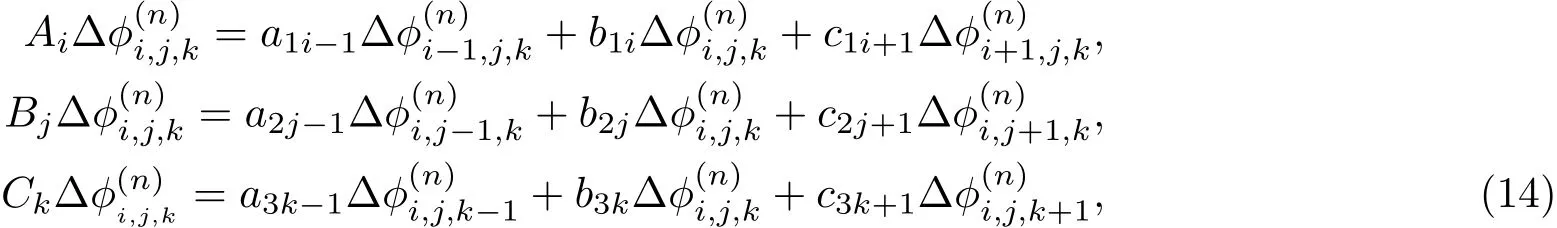
則最終的電勢方程迭代計算式為

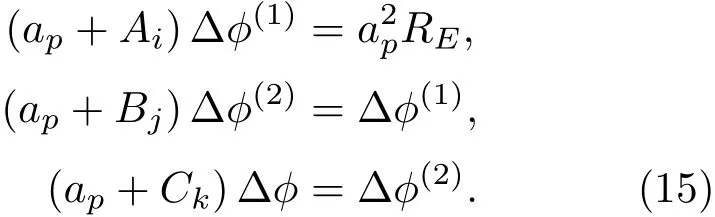
霍爾電場邊界條件為:絕緣壁面,J·n=0;導電壁面,?=0;其余邊界為NeuMann邊界,??·n=0.

3 數值驗證

驗證算例1取自參考文獻[13],其控制方程為??=xez.該方程擁有解析解?=xez.若令則其控制方程可以化為和(2)式同樣的簡化形式.給定Dirichlet邊界條件:?=xez.圖1給出了兩套計算網格:單分區正方體網格和三分區球頭網格.其中,正方體網格計算域為x=[0,1],y=[0,1],z=[0,1],球頭半徑為0.5m.從圖2中兩種網格數值解和解析解的對比可以看出,二者符合良好,驗證了數值方法對不同網格的適應性.

驗證算例2為間隔電極霍爾效應算例,如圖3所示[13].±Y的通道邊界內通入+X方向的導電流體,電導率σ=1??1·m?1.有限寬度的平行電極沿周期性重復布置在通道兩側壁面上.由于通道無限長,圖3中的Inlet和Outlet邊界設置為周期性邊界.為使通道內流體速度場對電勢場結果無影響,則必須滿足?×(u×B)=0,因此可假定u=f(y),B=f(z),且通道內流動為充分發展的Poiseuille流動,如(16)式所示:

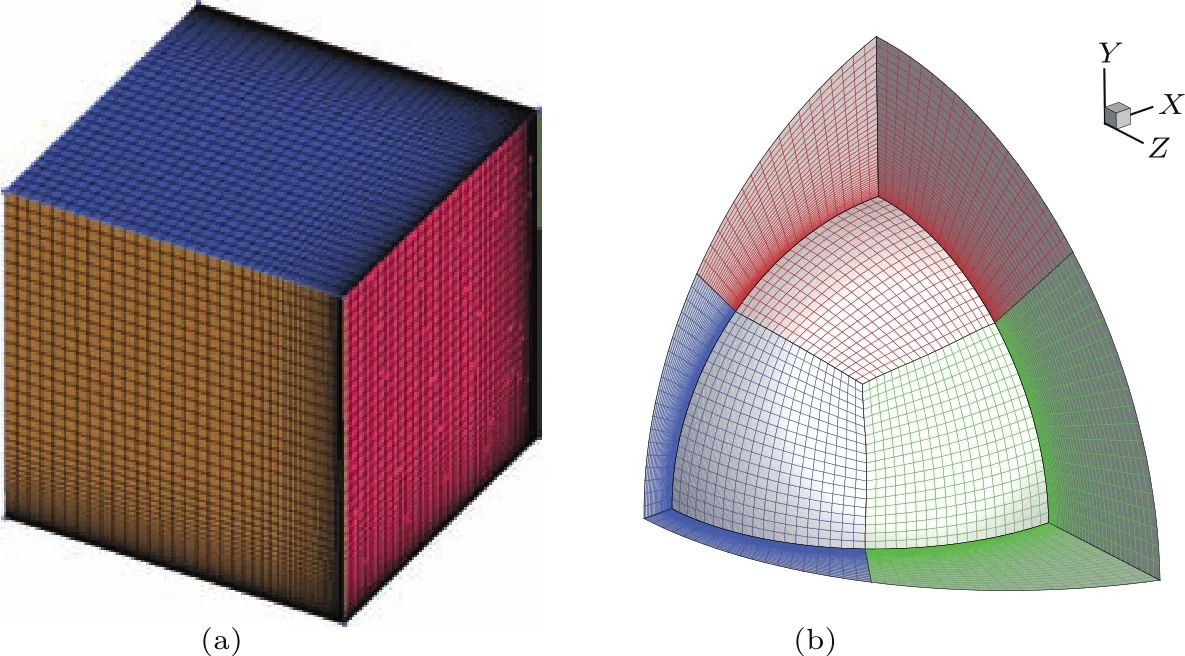
圖1 (網刊彩色)驗證算例1的兩套網格(a)單分區立方體;(b)三分區1/4球頭Fig.1.(color on line)Two Meshes for validation case 1:(a)Cube of single segMent;(b)quarter sphere head of th ree segMents.

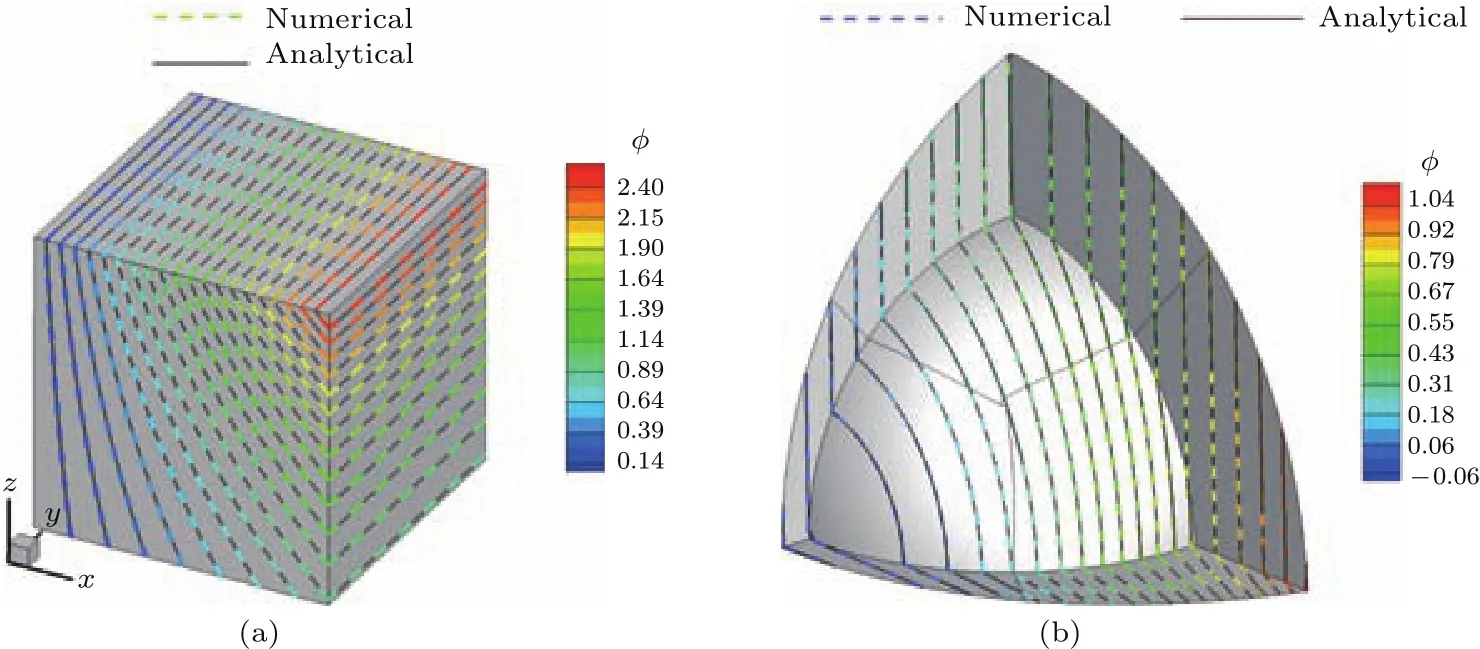
圖2 (網刊彩色)驗證算例1的數值解和解析解對比(a)立方體網格;(b)球頭網格Fig.2.(color on line)CoMparison of nuMerical and analytical resu lts:(a)Cube Mesh;(b)quarter sphere head Mesh.

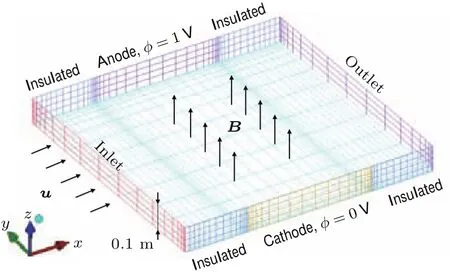
圖3 (網刊彩色)間隔電極霍爾效應算例示意圖Fig.3.(color online)ScheMatic view of segMented electrodes.

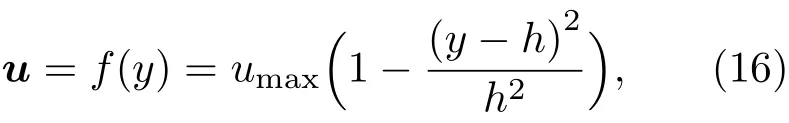
其中,umax為通道中心線上的流體速度,umax=1m/s.h為通道半寬,h=0.5m.

當B=0 T時,兩電極間只存在靜電場.圖4和圖5分別給出了無霍爾效應時本文和文獻[17]的電勢等值線、電流流線對比.圖6給出了有霍爾效應時(β=1.0,B=1 T)時的本文與文獻[13]的電流流線對比.可以看出,兩種情況下,本文計算結果與文獻[13]的結果符合良好.

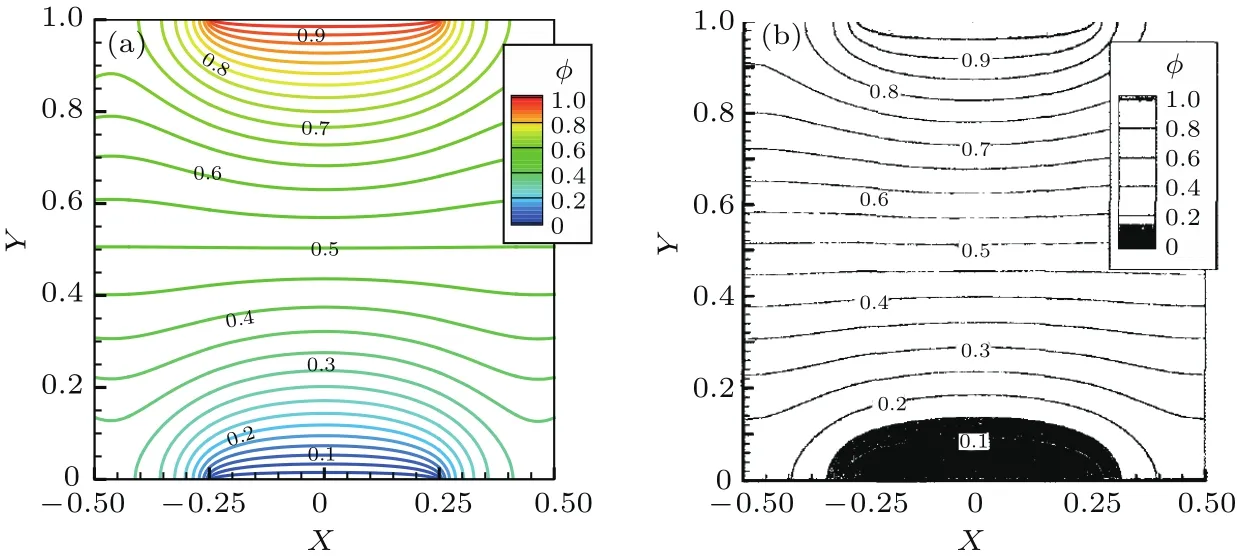
圖4 (網刊彩色)無霍爾效應時靜電場電勢等值線對比圖(a)本文結果;(b)文獻[13]結果Fig.4.(color on line)E lectric potential contou rs for the segMented electrode channelw ithou tMagnetic field:(a)Our results;(b)Ref.[13].

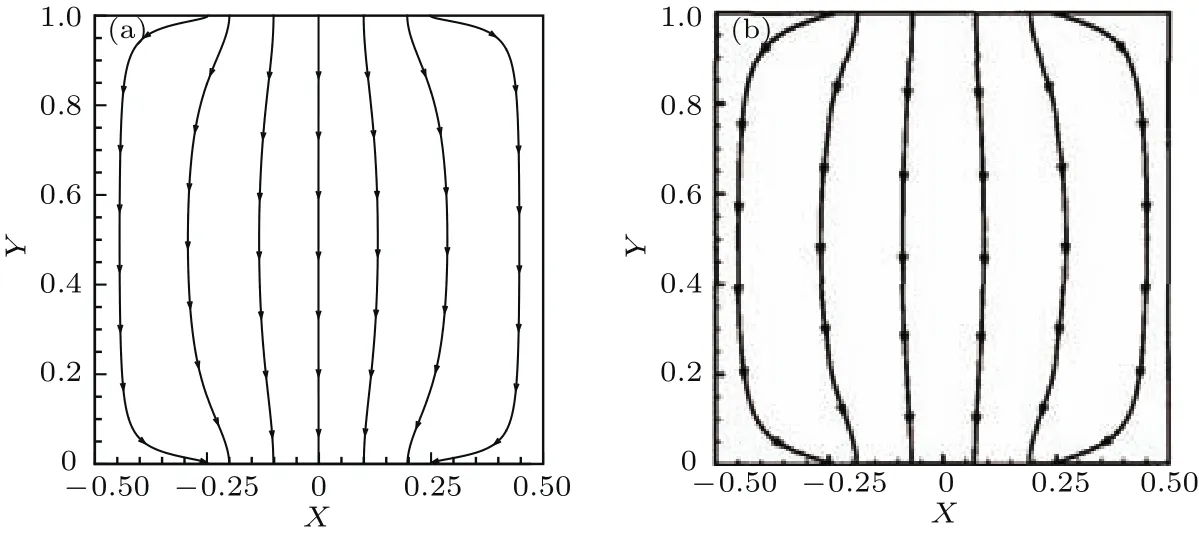
圖5 無霍爾效應時靜電場電流線對比圖(a)本文結果;(b)文獻[13]結果Fig.5.E lectric cu rrent streaMlines w ithout Magnetic field:(a)Ou r resu lts;(b)Ref.[13].

圖6 有霍爾效應(β=1.0)時靜電場電流線對比圖(a)本文結果;(b)文獻[13]結果Fig.6.E lectric current streaMlines w ith Hall eff ect(β=1.0):(a)Our resu lts;(b)Ref.[13].

4 霍爾電場收斂性分析

4.1 步進因子a p

由(15)式可以得到i向的系數矩陣如(7)式所示.可以看出,步進因子ap在迭代計算中的主要作用是保證迭代矩陣對角占有.因此,ap的合適取值應和a,b,c三個系數的大小有關.ap取值過大會造成收斂速度緩慢;過小則無法保證系數矩陣對角占優,使得計算發散.

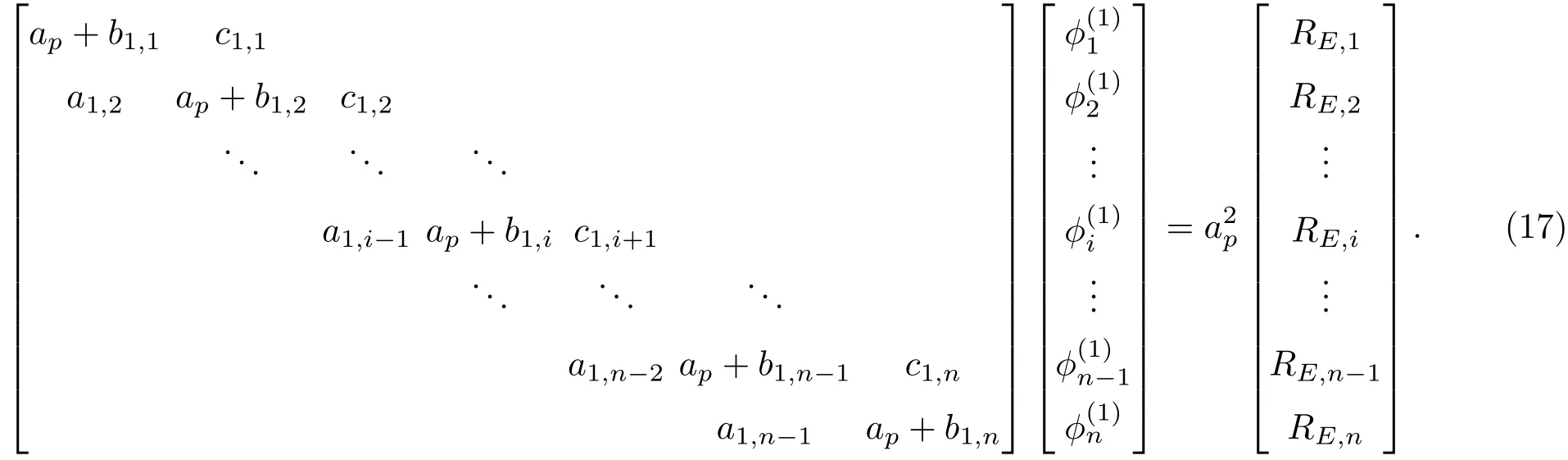
根據(10)式和(12)式可以看出,系數b1∝ξnσ1i,n=x,y,z;i=1,2,3.因此ap的取值與網格尺度以及電導率、霍爾系數都有關系.網格越密,ξn越小,相應的系數a,b,c越小,ap可以取值更小.這里選用驗證算例1立方體網格進行計算,分析不同網格尺度下ap的取值對電場收斂性的影響.

圖7為三套網格下(10×10×10,30×30×30,50×50×50)不同ap取值對應的電勢收斂曲線.可以看出,對應每套網格都存在一個最優的步進因子ap使得電勢收斂速度最快;隨著網格尺度的減小,最優步進因子減小,三套網格對應的最優步進因子分別約為0.125,0.015,0.006,與之前理論分析一致.

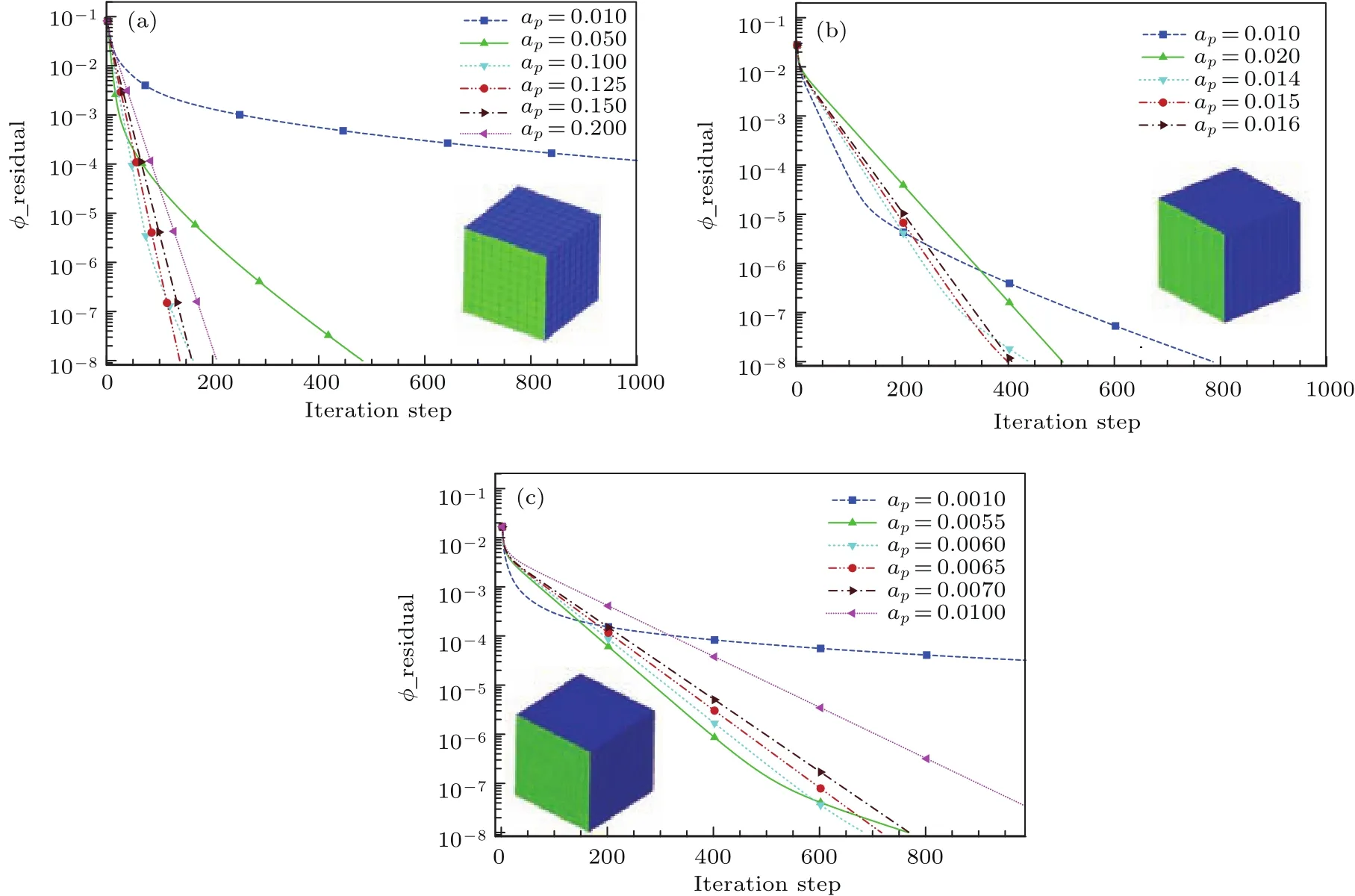
圖7 (網刊彩色)不同網格尺度下不同a p取值的電場收斂曲線(a)10×10×10;(b)30×30×30;(c)50×50×50Fig.7.(color on line)Residual cu rves of electric potential under various stepping factors for diff erent grid densities:(a)10×10×10;(b)30×30×30;(c)50×50×50.

4.2 霍爾系數的影響

選用日本1996年發射的軌道再入試驗飛行器(orbital reentry experimental,OREX)返回艙前體作為計算模型.計算域和網格分別如圖8所示.選取再入飛行時間在7461.5 s飛行工況(Ma=20.04,H=63.60 km).駐點磁感應強度B0=0.2 T,霍爾系數β=1.0,5.0,10.0.采用全催化、絕緣壁面條件.

圖9給出了不同霍爾系數下不同ap的電勢收斂曲線.ap取值小于圖中的最小值時即發散.可以看出,霍爾系數β=1.0,5.0,10.0對應的最優ap分別約為1.0×10?3,2.0×10?3,4.0×10?3,并且當收斂至電勢殘差為1.0×10?4時,需要的虛擬迭代步數分別為900,8900,31000步.可見,網格一定,對應某個霍爾系數存在一個最優的步進因子ap,并且隨著霍爾系數的增加,最優步進因子ap增加,電勢場收斂速率變慢.

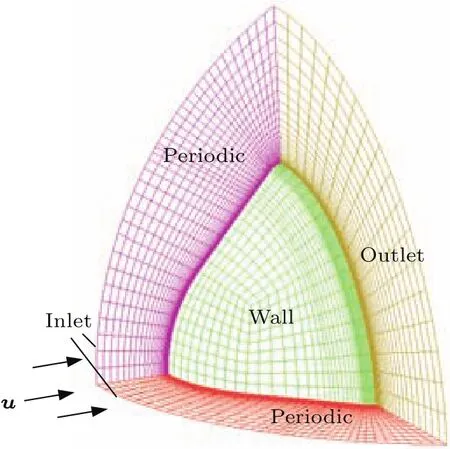
圖8 (網刊彩色)軌道再入試驗飛行器的幾何模型、網格及邊界示意圖Fig.8.(color online)GeoMetry and boundary conditions of OREX.

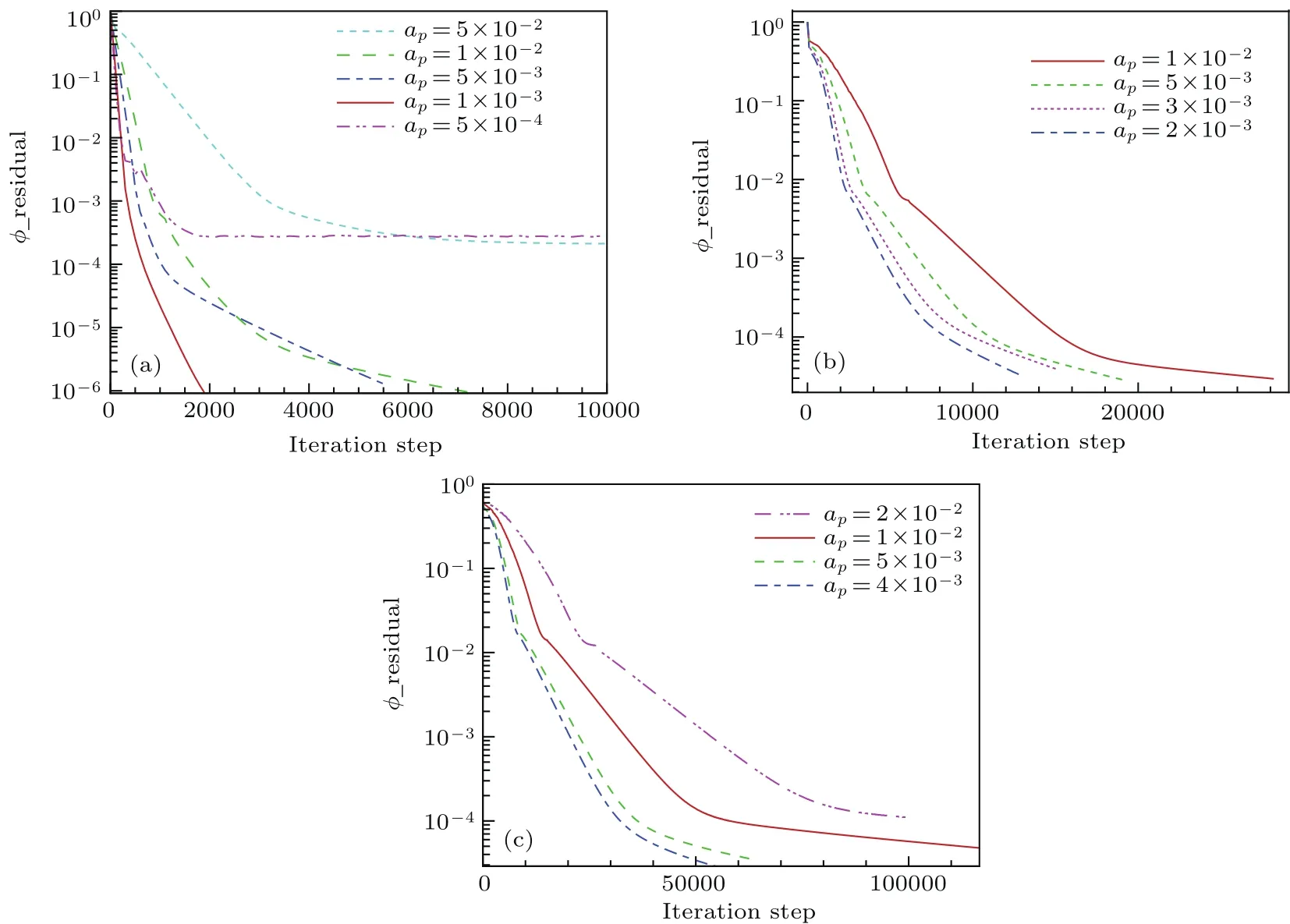
圖9 (網刊彩色)不同霍爾系數下不同a p的電勢收斂曲線(a)β=1.0;(b)β=5.0;(c)β=10.0Fig.9.(color on line)Residual curvesunder variousstepping factors for diff erent HallparaMeters:(a)β=1.0;(b)β=5.0;(c)β=10.0.

5 變步進因子加速法

由上節分析可知,步進因子的最優取值和網格尺度、霍爾系數相關.不同網格尺度、霍爾系數下,最優步進因子差別較大.氣動熱計算網格不均勻程度高并且霍爾系數也隨著外加磁感應強度、飛行狀態的改變變化較大,這些都給固定步進因子的取值帶來困難.因此,實際流場各點的ap可以取不同值,以在當地網格尺度和當地霍爾系數下都達到較優的收斂效果.由于ap的主要作用是在計算中保證元素b1,b2,b3對角占優,故參考計算流體力學中當地時間步長的做法,令

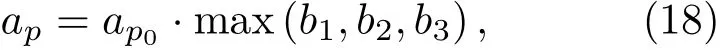
其中,ap0為常系數.圖10給出了驗證算例1局部加密立方體網格不同ap0下的電勢收斂曲線.其中,圖10(a)為X向加密網格,圖10(b)為三向均加密網格.圖中實心和空虛曲線分別代表全局定ap和當地變ap收斂曲線.可以看出,對于局部加密網格而言,變ap條件下的電勢收斂性明顯優于定ap.盡管變ap條件下同樣需要確定最優的步進因子系數ap0,但其范圍相對比較固定.較優的取值范圍位于0.01—0.50之間,具體取值要根據實際網格和霍爾系數確定.

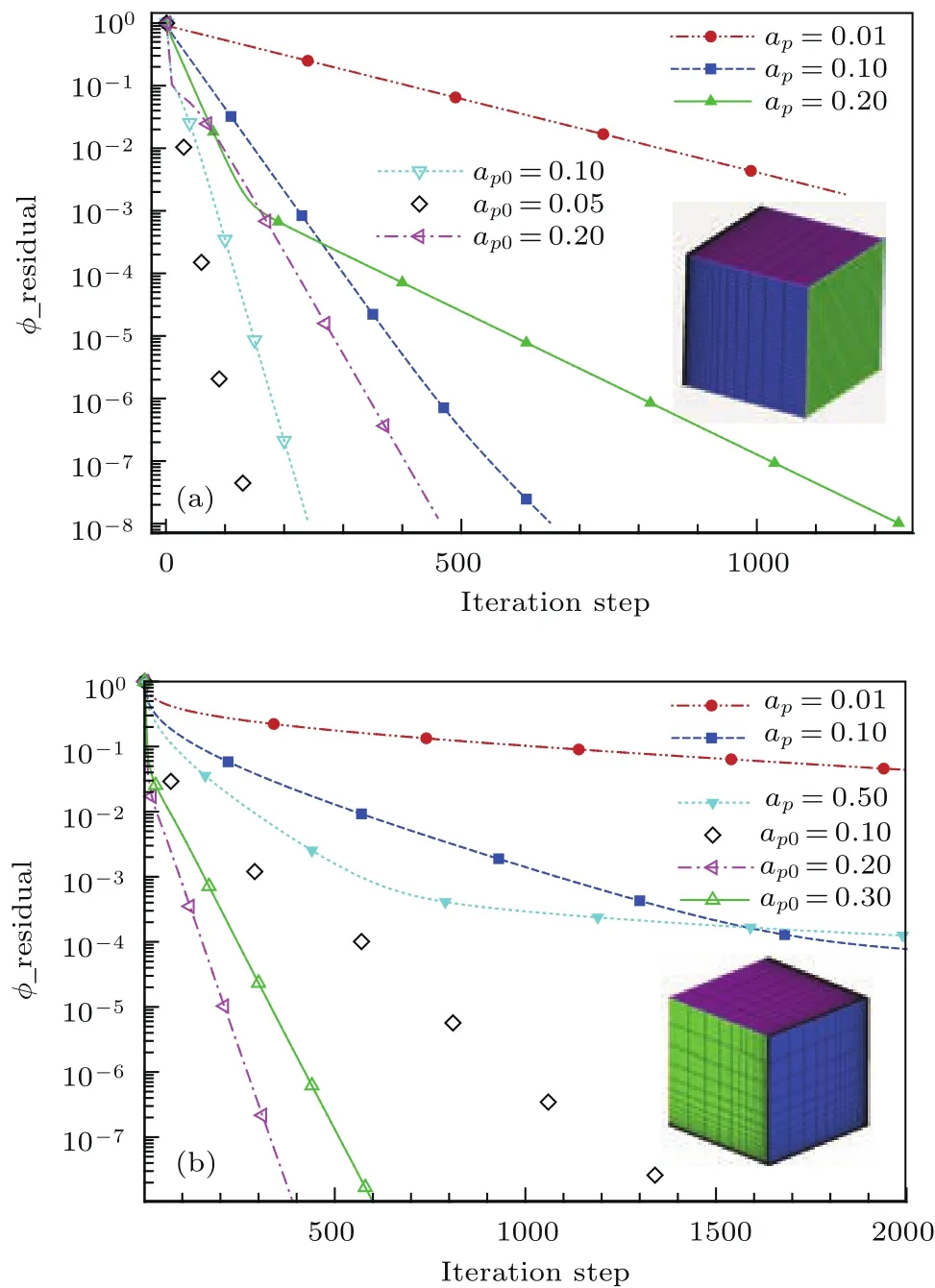
圖10 (網刊彩色)不同步進因子下的電勢收斂曲線(a)X向加密;(b)三個方向加密Fig.10.(color on line)Residual curves under various stepp ing factor for d iff erent refined Meshes:(a)Refined in the X direction;(b)refined in three directions.

6 結論

針對高速飛行器磁控熱防護系統霍爾電場的求解問題,采用交替隱式近似因子分解法,建立了熱化學非平衡條件下的電勢Poisson方程數值方法,并采用標準算例完成了程序驗證.而后從迭代矩陣性質出發,分析了步進因子ap和電場收斂性的關系以及影響步進因子取值的因素(網格尺度、霍爾系數),并參考計算流體力學中當地時間步長加速收斂的方法,提出了當地變步進因子加速電場收斂方法.研究表明:

1)在網格和霍爾系數一定的情況下,存在一個最優的步進因子ap使得霍爾電場收斂速度最快;

2)隨網格尺度的減小和霍爾系數的增加,最優步進因子ap變大,電勢場收斂速率變慢;

3)對于局部加密網格而言,當地變步進因子方法的電勢收斂性明顯優于常規的定步進因子法.

[1]Zhu Y J,Jiang Y S,Hua H Q,Zhang C H,X in C W 2014 Acta Phys.Sin.63 244101(in Chinese)[朱艷菊,江月松,華厚強,張崇輝,辛燦偉2014物理學報63 244101]

[2]Y in J F,You Y X,LiW,Hu T Q 2014 Acta Phys.Sin.63 044701(in Chinese)[尹紀富,尤云祥,李巍,胡天群2014物理學報63 044701]

[3]Zhao G Y,Li Y H,Liang H,Hua W Z,Han MH 2015 Acta Phys.Sin.64 015101(in Chinese)[趙光銀,李應紅,梁華,化為卓,韓孟虎2015物理學報64 015101]

[4]Yu H Y 2014 Acta Phys.Sin.63 047502(in Chinese)[于紅云2014物理學報63 047502]

[5]Bityu rin V A,Bocharov A N 2014 52nd Aerospace Sciences Meeting National Harbor,Mary land,January 13–17,2014

[6]Bisek N J,Gosse R,Poggie J 2013 J.Spacecraft Rockets 50 927

[7]C ristofolini A,BorghiC A,NerettiG,Battista F,Schettino A,Trifoni E,Filipp is F D,Passaro A,Baccarella D 2012 18th A IAA/3AF In ternational Space P lanes and Hypersonic SysteMs and Techno logies Conference Tours,France,Sep teMber 24–28,2012

[8]Lv H Y,Lee C H 2010 Chin.Sci.Bu ll.55 1182(in Chinese)[呂浩宇,李椿萱2010科學通報55 1182]

[9]Li K,Liu W Q 2016 Acta Phys.Sin.65 064701(in Chinese)[李開,劉偉強2016物理學報65 064701]

[10]Hu H Y,Yang Y J,Zhou W J 2011 Chin.J.Theo.App.Mechan.43 453(in Chinese)[胡海洋,楊云軍,周偉江2011力學學報43 453]

[11]Gaitonde D V,Poggie J 2002 40th A IAA Aerospace Sciences Meeting and Exhibit Reno,Nevada,January 14–17,2002

[12]W an T,Cand ler G V,Macheret SO,Shneider MN 2009 A IAA J.47 1327

[13]Bisek N J 2010 Ph.D.D issertation(Michigan:University of Michigan)

[14]Lv H Y,Lee C H,Dong H T 2009 Sci.Sin.Phys.Mechan.Astron.39 435(in Chinese)[呂浩宇,李椿萱,董海濤2009中國科學G輯39 435]

[15]Peng W,He Y G,Fang G F,Fan X T 2013 Acta Phys.Sin.62 020301(in Chinese)[彭武,何怡剛,方葛豐,樊曉騰2013物理學報62 020301]

[16]Fu jino T,MatsuMoto Y,Kasahara J,Ishikawa M2007 J.Spacecraft Rocket 44 625

[17]Holst T 2000 Progress in Aerospace Sci.36 1

[18]Zhang K P,D ing G H,T ian Z Y,Pan S,Li H 2009 J.National Univ.Defense Tech.31 39(in Chinese)[張康平,丁國昊,田正雨,潘沙,李樺2009國防科技大學學報31 39]

[19]T ian Z Y,Zhang K P,Pan S,Li H 2008 Chin.Quar.Mechan.29 72(in Chinese)[田正雨,張康平,潘沙,李樺2008力學季刊29 72]

[20]Gnoff o P A,Gup ta R N,Shinn J L 1989 NASA TP–2867

(Received 16 Sep teMber 2016;revised Manuscrip t received 22 January 2017)

PACS:47.40.Ki,47.85.L–,52.30.Cv,41.20.GzDOI:10.7498/aps.66.084702

*Project supported by the Natural Science Foundation of Hunan Province,China(G rant No.13JJ2002)and the National Natu ral Science Foundation of China(G rant No.90916018).

?Corresponding author.E-Mail:LiKai898989@126.com

N uMerical so lu tion p rocedu re for H all electric fi eld of the hyperson ic Magnetohyd rodynaMic heat sh ield system?

Li Kai?Liu Jun Liu Wei-Qiang

(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)

MagnetohydrodynaMic(MHD)heat shield systeMis a novel-concept thermal protection technique for hypersonic vehicles,which hasbeen proved by lotsof researchersw ith both nuMericaland experiMentalMethods.Most of researchers neglect the Hall eff ect in their researches.However,in the hypersonic reentry process,the Hall eff ect is soMetiMes so significant that the electric current distribution in the shock layer can be changed by the induced electric field.Consequently,the Lorentz force aswellas the Joule heat is varied,and thus the effi ciency of the MHD heat shield systeMis aff ected.

In order to analyze the influence of Halleff ect,the induced electric field must be taken into consideration.According to the weakly-ionized characteristics of hypersonic flow post bow shock,the Magneto-Reynolds number is assuMed to be sMall.Therefore,the Maxwell equations are siMp lified w ith the generalized Ohm’s law,and the induced electric field is governed by the potential Possion equation.Numericalmethods are hence established to solve the Hall electric field equations in the therMocheMical nonequilibriuMflow field.The electric potential Poisson equation is of significant rigidity and diffi cult to solve for two reasons.One is that the coeffi cientmatrix may not be diagonally doMinant when the Hall parameter is large in the shock layer,and the other is that thismatrix including the electric conductivity is discontinuous across the shock.In this paper,a virtual stepping factor is included to strengthen the diagonal doMinance and iMp rove the coMputational stability.Moreover,approximate factor and alternating direction iMp licit method are eMp loyed for further iMp roving the stability.W ith these Methods,a FORTRAN code is w ritten and validated by coMparing the nuMerical resultsw ith the analytical ones aswell as results available froMprevious references.A fter that,relation between the convergence property and the virtualstepping factor is revealed by theoreticalanalysisand numerical simulations.Based on thesework,a local variable stepping factorMethod is p roposed to accelerate the iterating process.Resu lts show that the convergence property is closely related to theMesh density and Hall paraMeter,and there exists a best stepping factor for a particu larmesh aswell as a particular Hall parameter.Since the best stepping factor varies a lot for diff erentMeshes and diff erent Hall paraMeter,its appropriate value is hard to choose.The best value of stepping factor coeffi cient still exists in the local step factor Method,but its value range is relatively sMaller.More iMportantly,the local stepping factor method yields better convergence property than the regular constant one when eMp loying a locally refined Mesh.

magnetohydrodynaMic flow control,thermal protection,Hall eff ect,Poisson equation

10.7498/aps.66.084702

?湖南省自然科學基金(批準號:13JJ2002)和國家自然科學基金(批準號:90916018)資助的課題.

?通信作者.E-Mail:LiKai898989@126.com

?2017中國物理學會C h inese P hysica l Society

http://w u lixb.iphy.ac.cn