基于改進的集對分析方法在河流健康評價中的應用

舒持愷,楊 侃

(河海大學水文水資源學院,江蘇南京210098)

基于改進的集對分析方法在河流健康評價中的應用

舒持愷,楊 侃

(河海大學水文水資源學院,江蘇南京210098)

考慮到河流健康評價系統中存在的不確定性問題,引入集對分析理論(SPA),并改進其聯系度的計算,以灰色聚類理論中的不同灰類的聚類系數取代相應的聯系度分量；同時針對傳統灰色聚類理論中的白化函數覆蓋范圍小的問題,用改進的指數型白化函數建立樣本等級對應關系,并利用兩階段層次分析法(AHP)進行指標權重的計算。以某市河流H為例對建立的評價指標、評價標準和評價方法進行了驗證應用,結果顯示該方法能夠很好地處理評價體系中的不確定性和復雜性因素,適用于河流健康評價。

河流健康評價；改進白化權函數；集對分析理論；層次分析法；不確定信息

0 引 言

健康的河流不僅需要保持生態學意義上的完整性,還應強調對社會服務功能的發揮[1-2]。當前河流健康評價方法很多,各有各的利弊。鑒于河流本身存在的許多不確定性因素,引入集對分析理論(SPA),可以很好地處理河流評價系統中不確定性問題[3]。但傳統的集對分析理論中聯系度計算過于簡單,本文引入灰色聚類理論,以不同灰類的聚類系數表示相應的聯系度分量。同時，針對傳統灰色聚類法的白化函數覆蓋范圍小的問題,做出改進,用指數型白化函數建立樣本值與各等級之間的對應關系,充分利用已知信息淡化未知信息,客觀真實地反映系統本質[4]；并用改進層次分析法(AHP)進行指標權重的計算；最后，通過實例驗證了該方法的可行性和合理性。

1 構建河流健康評價指標體系

在進行河流健康評價之前,需篩選出評價指標,要求能夠準確客觀地反映出河流生態環境狀況及變化趨勢。主要從三方面考慮：①評價指標的獨立性；②從定性方面最能反映河流健康的程度指標(專家咨詢、群眾問訪)；③指標數據可以實測取得。本文依照相關原則,經綜合考慮某市河流基本情況,從自然環境子系統和社會服務子系統進行評價指標篩選,從而建立了四層指標體系[1-2,5](見表1)。

表1 河流健康評價體系層次劃分

準則層部分指標含義的說明如下：

(1) “河岸穩定性”指標D1定義為穩定無明顯侵蝕的河岸線長度占河岸線總長度的比例,；“穩定無明顯侵蝕的河岸”包括有良好植被覆蓋的自然土質岸坡及人工護坡如漿砌石、混凝土岸坡。

(2)“生態流量滿足程度指數” D3是指河流控制斷面或特征斷面對河流最小生態需水量的滿足程度。

(3)“公眾滿意度”D9是指公眾對評價河流景觀、美學價值及其他綜合服務功能的滿意程度。采用公眾參與調查統計方法進行。

(3)“水功能區水質達標率” D11這一指標可以反映河流對飲用水水源地、漁業養殖、工業、農業、景觀娛樂等供水功能的水質滿足情況。

本文將指標等級分為優、良、中、差4個級別(見表2)。等級標準以文獻[5]為參考。

2 引入灰色聚類理論改進集對分析方法

2.1 集對分析理論(SPA)

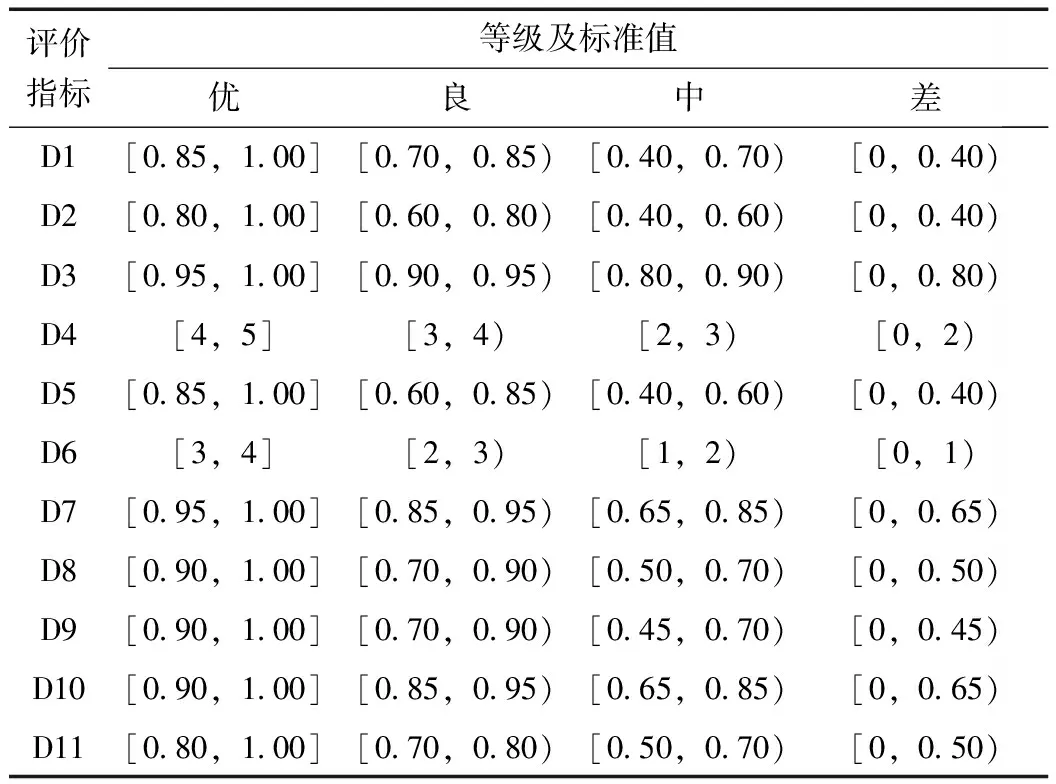
表2 評價指標等級劃分標準

集對分析理論是我國學者趙克勤于1989年提出的一門處理不確定性問題的系統理論方法。它把研究的問題構建具有一定聯系的兩個集對,對集對中兩集合的特性進行同一、差異、對立的系統分析,然后用聯系度μ表達式定量刻畫[6-7]。對于各評價指標,可用下述公式計算聯系數。即

μk=ak+bki1+cki2+dkjk=1,2,…,n

(1)

ak+bk+ck+dk=1ak、bk、ck、dk∈[0,1]

(2)

式中,ak、bk、ck、dk稱為聯系度分量；ak反映了指標k對等級優的偏向度；bk反映了對等級良的偏向度；ck反映了對等級中的偏向度；dk反映了對等級差的偏向度。可取i1=0.33,i2=-0.33、j=-1,則各指標k的四元聯系數μk取值在[-1,1]之間,評判標準如表3。

表3 聯系數 μk的評價標準

對于河流健康評價中n個指標體系,分析步驟如下：

(1)根據樣本數據,按式(3)計算各個指標的四元聯系數μk,并按照表3的標準進行判斷,得到河流各個指標k的評價等級

ak=μk1,bk=μk2,ck=μk3,dk=μk4

(3)

式中,μk1、μk2、μk3、μk4分別是指標k對應的4種不同灰類等級下的聚類系數。

(2)結合各個指標的權重,對n個指標的聯系數μk進行加權平均,按下式計算得到總體聯系數μ,再對其進行分析總結。即

(4)

式中,ωk為指標k的權重。本文通過改進的層次分析法計算得到。

2.2 改進集對分析方法

結合集對分析理論與灰色聚類法,采用優、良、中、差4個灰類分級標準,并將指標相應的聚類系數按式(3)取代聯系度分量。

傳統聚類白化函數采用“升降半梯形”結構,只考慮了相鄰等級評價值的影響,如果評價值在相鄰等級以外,其白化函數值便為零,當樣本數據過于分散時,可能會丟失很多重要信息,使評價結果出現誤差[8-10]。因此,本文構造指數型白化函數,改進后的函數曲線是平滑的,擴大了函數覆蓋范圍,有效解決了零權重問題。

定義ykp是指標k隸屬于灰類等級p的評價標準值,每個指標有m個灰類等級,xqk是樣本q對應于指標k的樣本數據值,fkp(xqk)是樣本q的指標k隸屬于灰類等級p的白化函數,則相應的白化函數值計算式

(5)

(6)

(7)

對應的白化函數圖像如圖1所示。其中,圖 a、b、c分別對應于白化函數表達式(5)、(6)、(7)。

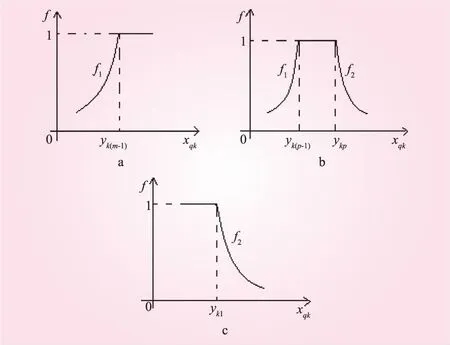
圖1 指數型白化函數圖像

利用式(5)～(7)計算得到各指標在不同灰類等級下的聚類系數,再對其進行歸一化處理。即

(8)

再由式(3)即可得到改進后的聯系度分量。由于引入指數型白化函數,使得聯系度分量的計算更為合理,比較好地體現了各個指標等級間的相互聯系。

2.3 計算指標權重

本文通過二階段層次分析法(AHP)進行指標權重的計算。傳統的(1～9)九標度法,專家和決策者很難掌握標度的標準,尤其是當比較指標過多時,更容易產生混亂,從而判斷矩陣一致性效果較差。因此,本文采用構造矩陣的兩階段法[11]：第一階段,采用容易判斷的的(0,1,2)三標度法來對每一個元素進行兩兩比較后,建立一個比較矩陣；第二階段,通過變換將比較矩陣轉化為判斷矩陣,并進行一致性檢驗。具體步驟如下：

(1)將研究問題進行分層,建立遞階層次結構,清楚地表明各層次之間的關系。

(2)用三標度法對同一層元素進行兩兩比較后建立比較矩陣An×n。

(4)由判斷矩陣得出權重ω,并檢查判斷矩陣Cn×n的一致性是否可以接受。

2.4 改進集對分析方法計算流程圖

為了直觀地描述計算方法過程,繪制了改進集對分析方法計算流程圖(見圖2)。

圖2 計算流程示意

3 實例應用

河流H貫穿某市南北,河道長約23.6 km,是省水系規劃中確定的區域骨干4級河道,是該市主要航道之一；同時對南北河道水位起著很重要的調節作用。隨著上游地區和該市相關鎮區工業化和城市化步伐加快,在自然與人類活動雙重脅迫作用下,該河流健康狀況受到一定程度的影響,需要對其健康情況做出評價。數據資料來自現場調研、采樣以及當地水利農機局部門提供。在實地調研過程中,將河流分段,設置檢測取樣斷面,全程踏勘,一定程度上保證了資料的可靠性。將獲取到的數據資料,應用上述指數型白化函數方法計算,得到2015年該河流11項指標的四元聯系數,并進行分析,結果見表4、圖3和圖4。

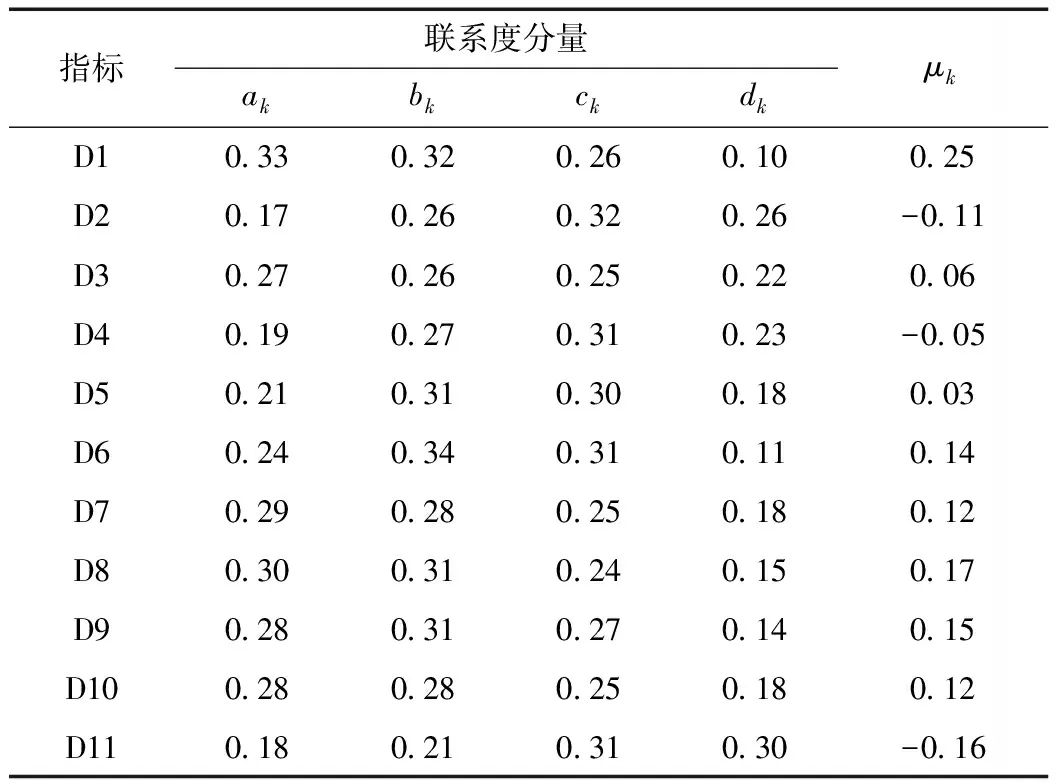
表4 河流健康指標評價結果

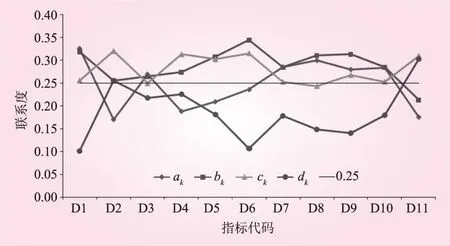
圖3 各指標四元聯系度分量

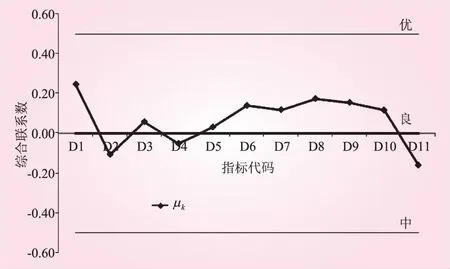
圖4 各指標綜合聯系數 μk

由表4、圖3、4可以看出：

(1)各指標的聯系度分量ak,它體現的是該指標偏向等級優的程度。其中河岸穩定性指數(D1)、生態流量滿足程度指數(D3)、防洪工程達標率(D7)、岸線利用管理指數(D8)、公眾滿意度(D9)、供水量保證率(D10)的ak值達到0.25(四元聯系數的平均值)以上,表明該河流在這些方面狀況優良。

(2)各指標的聯系度分量dk,它體現的是該指標偏向等級差的程度。其中,河流流動性指數(D2)、水功能區水質達標率(D11)的dk值超過了0.25,生態流量滿足程度指數(D3)、水質綜合指數(D4)的dk值接近0.25,說明河流的流動性較差；同時水質存在污染情況。這也體現了河流的流動性與水體污染的關系,即流動性較差的河流往往容易受到污染。

(3)各指標的聯系數μk,它體現的是該指標的總體水平。其中,河流流動性指數(D2)、水質綜合指數(D4)、水功能區水質達標率(D11)的μk值小于零(等級良標準值),其余的指標均大于零。根據表3的標準劃分,雖然河流的D2、D4、D11為中等水平,但對比其余的指標,也說明了該河流在流動性和水質方面有待改善。

根據改進的層次分析法進行11項指標權重的計算,得到權重值ω為[0.028,0.024,0.130,0.182,0.040,0.066,0.028,0.028,0.078,0.215,0.182]。結合表4中各指標的μk值,由式(3)求得河流總體的四元聯系數μ值為0.029,由表3得到評價等級為中,與實際情況相符。

綜上所述,H河2015年的評價等級為中等,健康狀況較差,雖然能夠較好地滿足周邊區域居民用水需求,但河流水質較差,流動性也不好,存在污染。今后,應當加大監管力度,控制河流污染,改善水質,恢復良好的水生態環境。同時河流兩岸的防洪工程建設較好,應當充分利用好河流的防洪設施抵御洪水災害。

4 結 語

(1)本文引入改進的指數型白化函數進行聯系度的計算,克服了傳統白化函數覆蓋等級范圍窄問題,準確包含了更多評價指標中的不確定信息；同時,利用二階段層次分析法進行權重的計算,也比較方便合理。應用實例表明,該方法適用于河流健康評價。

(2)指數型白化函數雖然覆蓋等級廣,但函數曲線在相鄰等級內下降較快,而在相鄰等級之外趨于平緩,不知這樣是否合理,還有待研究。

(3)河流健康評價的指標有很多,本文篩選的11個指標可能存在不足,今后還需深入研究探討,逐步加以完善。

[1]耿雷華, 劉恒, 鐘華平, 等. 健康河流的評價指標和評價標準[J]. 水利學報, 2006, 37(3)： 253- 258．

[2]卞錦宇, 耿雷華, 方瑞. 河流健康評價體系研究[J]. 中國農村水利水電, 2010(9)： 39- 42．

[3]王穎, 邵磊, 楊方廷, 等. 改進的集對分析水質綜合評價方法[J]. 水力發電學報, 2012, 31(3)： 99- 106．

[4]鄧聚龍. 漢英對照灰色系統基本方法[M]. 2版. 武漢： 華中科技大學出版社, 2005．

[5]李浩, 楊侃, 陳靜, 等. 灰色三角白化權集對分析模型在河流健康評價中的應用[J]. 水電能源科學, 2015, 33(8)： 33- 36．

[6]趙克勤. 集對分析對不確定性的描述和處理[J]. 信息與控制, 1995, 24(3)： 62- 166．

[7]趙克勤, 宣愛理. 集對論——一種新的不確定性理論方法與應用[J]. 系統工程, 1996, 14(1)： 18- 23．

[8]馬艷琴, 楊紅艷, 潘平奇. 灰色聚類關聯分析法的改進及其應用[J]. 數學的實踐與認識, 2013, 43(19)： 166- 172．

[9]胡軍, 許麗忠, 張江山. 基于改進灰色聚類法的大氣環境質量綜合評價[J]. 福建師范大學學報： 自然科學版, 2012, 28(1)： 49- 54．

[10]閆濱, 孫友良, 于保慧. 基于改進白化權函數灰色聚類法的水閘安全評價[J]. 沈陽農業大學學報, 2015, 4(2)： 245- 249．

[11]朱茵, 孟志勇, 闞叔愚. 用層次分析法計算權重[J]. 北京交通大學學報, 1999, 23(5)： 119- 122．

(責任編輯陳 萍)

RiverHealthAssessmentBasedonImprovedSetPairAnalysisMethod

SHU Chikai, YANG Kan
(College of Hydrology and Water Resources, Hohai University, Nanjing 210098, Jiangsu, China)

Considering the uncertainty problem in the assessment system of river health, the Set Pair Analysis (SPA) theory is introduced, and its connection degree calculation is improved by using the clustering coefficients of different grey classes in grey clustering theory to replace corresponding connection degree. At the same time, for solving the problem of small sample coverage of Definite Weighted Function in traditional grey clustering theory, the improved Definite Weighted Function of exponential type is used to set up sample level corresponding relation, and two-phase Analytic Hierarchy Process (AHP) is used to calculate index weight. The application of above method in River H verifies the index, criteria and method of assessment. The results show that the method can handle the uncertainty and complexity factors in assessment system well, and so it is suitable for river health assessment．

river health assessment; improved Definite Weight Function; Set Pair Analysis theory; Analytic Hierarchy Process; uncertain information

2016- 06- 14

國家重點基礎研究發展973計劃(2012CB417006)；“十一五”國家科技支撐計劃(2009BAC56B03)

舒持愷(1992—),男,安徽安慶人,碩士研究生,研究方向為水資源與水環境；楊侃(通訊作者)．

X826

：A

：0559- 9342(2017)06- 0001- 04