一種簡單的短時輻照度預測研究

鐘志峰，張 藝，張田田，楊晨茜，蘇 勇

(1.湖北大學 計算機與信息工程學院，武漢 430062；2.華中科技大學 光學與電子信息學院，武漢 430074 )

一種簡單的短時輻照度預測研究

鐘志峰1，張 藝1，張田田1，楊晨茜1，蘇 勇2

(1.湖北大學 計算機與信息工程學院，武漢 430062；2.華中科技大學 光學與電子信息學院，武漢 430074 )

準確的輻照度預測是光伏發電系統預測輸出功率的關鍵，而輻照度受緯度、天氣類型、海拔等因素的影響巨大，不同地區差異較大；目前對輻照度的短時預測研究中復雜的氣象數據獲取難度大，因此提出了一種利用便于獲取氣象數據進行輻照度短時預測的簡單方法；根據武漢市特有的地理位置特點，將天氣類型分為四類，將環境監測儀實時測量的溫度、輻照度數據及不同時刻的太陽高度角作為網絡的輸入，用多變量BP神經網絡模型對05:00到20:00時的每小時輻照度進行短期預測；將得到的預測結果與僅用歷史輻照度數據作為輸入得到的預測結果進行對比，該模型準確性有很大的提高；最終以持續性方法為基準得出預測技能；結果顯示該模型在A、B類天氣時預測技能均在0.75以上，大部分分布在0.80～0.85，表明該模型在僅利用便于獲取的氣象信息的基礎上能夠較準確地對短時輻照度進行預測。

輻照度短時預測；太陽高度角；BP神經網絡模型；預測技能

0 引言

太陽能是一種綠色無污染、潛能巨大、可持續發展的新型能源。目前對太陽能的利用主要是進行光伏并網發電，而光伏發電系統中輻照度是影響發電量的決定性因素。以往預測輻照度的算法大體可以分為兩類，一類是直接用歷史輻照度的數據進行單變量的預測，另一類是用溫度、氣壓、濕度、云層信息等氣象數據進行單變量或多變量的預測。其中復雜的氣象信息的搜集難度大，運算過程復雜，本文利用便于獲取的實時溫度數據和歷史輻照度數據，再結合整點時刻太陽高度角，以這3個量為輸入變量來預測05:00時到20:00時的輻照度。對輻照度進行預測的方法較常用的幾種模型有神經網絡算法模型[1-2]，經驗模型和統計分析[3]、小波變換算法模型[4-5]，支持向量機[6]，遺傳算法[7]模型等。每種算法模型都有各自的優勢和缺陷。由于輻照度的影響因素很多，能夠測得的影響因素與輻照度的關系是無法用特定函數描述的非線性關系。而BP神經網絡擁有強大的非線性擬合能力，在樣本充足的情況下，對內部機制復雜的系統進行求解十分方便,本研究正是利用該優勢來建立預測模型。將最終預測結果與持續性方法對比得出預測技能。

1 影響輻照度的因素

影響輻照度測量值大小的因素一般可以分為兩大類：一類是固有因素，如測試儀器自身的精確度及擺放的地理位置，儀器擺放角度等；另一類是外界環境因素，包括太陽高度角、天氣類型、總云量等。針對前一類因素，對輻照度預測的影響已經包含在歷史輻照度數據中；對于后一類因素，在某一特定地區，太陽高度和入射角是主要因素，天氣類型和云量是輻照度的反映量，為間接因素。由于云量信息很難獲取，考慮到輻照度的多少對環境溫度的高低有直接的影響，而實測溫度數據便于獲取，因此本文將太陽高度角和環境溫度作為預測輻照度的主要考慮因素。

1.1 太陽高度角

太陽光線與地平面的夾角即為某地點的太陽高度角，用e表示。地球的運動分為自轉和公轉，以地球為參照物，自轉造成了太陽高度角在一天之內不停的發生變化；公轉造成了太陽以年為周期在南北回歸線之間移動，因此太陽高度角的變化有日變化規律和年變化規律。其的計算公式為：

cos(90°-e)=sin(90°-δ)sin(90°-φ)cost+

cos(90°-δ)cos(90°-φ)

(1)

化簡可得：

sine=sinδsinφ+cosδcosφcost

(2)

式中，φ為本地的緯度值，δ為太陽赤緯角，t為太陽時角。φ、δ的取值均為北正南負；當e>0時，表示太陽在地平面之上(白天)；當e<0時，太陽在地平線之下(夜晚)。正午時t=0，上午為負，下午為正[8]。

太陽赤緯角δ的計算公式為：

(3)

其中：N為日期序號，1月1日為1，以此類推。本文地理緯度φ取北緯30.5°，太陽時角的計算公式為：

t=15×(ST-12)

(4)

式中，ST為真太陽時，以24小時計。

由本地實測數據得到的太陽高度角和輻照度的關系如圖1。

圖1 太陽高度角和輻照度的關系

從圖中可以看出輻照度和太陽高度角的變化趨勢相同，當太陽高度角增加時，輻照度也增加；太陽高度角減小時，輻照度也減小；太陽高度角到達峰值的時間略早于輻照度到達峰值時間。

1.2 溫度與輻照度的關系

輻照度是單位時間內投射到單位面積上的輻射能量，是影響環境溫度的主要因素。本文可通過環境監測儀獲得每一時刻該地環境溫度數據，輻照度與溫度的關系如圖2。

圖2 輻照度與溫度的關系

從圖中可以看出，兩者曲線變化趨勢相同，走勢雖不是完全對應，但輻照度增加時溫度增加，輻照度降低時溫度降低，因此溫度的高低可以在一定程度上反映該時刻的輻照度。

2 實現輻照度短時預測的模型

2.1 BP神經網絡模型的基本原理

BP神經網絡模型[9]采用信號正向傳播以及誤差反向傳播方式對網絡進行訓練。網絡可包含多變量輸入層，多個隱含層，多變量輸出層。BP神經網絡采用數據流的前向傳播和誤差信號的反向傳播機制，正向傳播時，每層神經元的狀態只影響下一層神經元。其中每個神經元的基本功能為加權、求和及轉移。每個神經元的輸入輸出如圖3。

圖3 每個神經元的輸入輸出示意圖

神經元輸出為式：

yj=f(Sj)

(5)

其中：

(6)

式中，x1,x2,…xi…xn分別代表來自前一層神經元1,2,…i…n的輸入；wj1,wj2,…wji…wjn則分別為上層對應神經元與該神經元的連接權值，令X=[x1,x2,…xi…xn]T，Wj=[wj1,wj2,…wji…wjn]，bj為閾值，f(·)為有界單調上升的傳遞函數，yj為第j個神經元的輸出。若令x0=1,wj0=bj，將這兩個量加入X和Wj向量中，則X=[x0,x1,x2,…xi…xn]T，Wj=[wj0,wj1,wj2,…wji…wjn]。

則節點j的凈輸入Sj可表示為：

(7)

該凈輸入量通過傳遞函數f(·)后，便得到此神經元的輸出yj為：

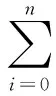
(8)

本文輸入變量有3個，輸出變量有16個，輸入樣本有800組，即n的值為3，m的值為16，s的值為800，每組樣本用a1,a2,…aq…as來表示，輸入第q個樣本時的輸出誤差為：

(9)

對于s個樣本，全局誤差為：

(10)

輸出層各神經元的權值調整公式為：

(11)

其中：wjk為隱含層與輸出層之間的權值，η表示學習率。

隱含層各神經元的權值調整公式為：

(12)

式中，vki為輸入層與隱含層之間的權值，η表示學習率。

4）低度相關指標：男女生肺活量分別與體重、身高、立定跳遠、坐位體前屈4項指標；立定跳遠分別與身高、坐位體前屈、50m、1000m或800m4項指標；50m分別與1000m或800m、引體向上或仰臥起坐2項指標；肺活量體重指數與坐位體前屈。除此之外，女生身高與50m、立定跳遠與仰臥起坐、坐位體前屈與體測總分，男生體重分別與50m、1000m、立定跳遠、引體向上、體測總分5項指標，男生坐位體前屈分別與1000m、引體向上2項指標，男生肺活量體重指數與所有身體素質測試指標都呈低度相關。

前向傳播與反向傳播交替進行，在權向量空間執行誤差函數梯度下降策略，動態迭代搜索一組權向量，使網絡誤差函數達到最小值，最終逼近期望輸出，進而完成信息提取和記憶過程。

2.2 BP神經網絡理論模型算法實現

通過對影響輻照度的相關因素的分析，結合多變量BP神經網絡模型綜合考慮太陽高度角和實測溫度數據建立預測模型，取一部分數據對神經網絡進行訓練，另外一部分數據用來驗證神經網絡預測精度。訓練階段，通過對樣本的學習，建立輸出與輸入之間的映射關系；在測試階段，利用該映射關系對新的輸入產生新的輸出，從而完成預測功能。本文模型的建模過程如下：

1)從數據庫讀取輻照度、溫度的所有歷史數據；

2)計算不同日期的每一時刻對應的太陽高度角；

3)設置訓練樣本和測試樣本；

4)設置神經網絡初始化參數，本文將神經網絡的訓練參數分別設置為目標誤差1e-6，學習速率0.05，最大訓練次數1000；

5)可以通過劃窗方式進行連續幾天的輻照度預測；

6)計算均方誤差和預測技能skill；

根據算法步驟得出流程圖如圖4。

圖4 算法流程圖

3 實驗結果及分析

本文所用到的軟件為MATLAB R2012b，數據取自武漢國際博覽中心光伏電站，共獲得2015年10、11、12月以及2016年1、2、3月共6個月的輻照度及溫度數據。數據庫中的數據是每隔兩分鐘一場，且每天的輻照度數據是從零開始的累積量，所以需要對數據進行預處理。從原始數據中整理出每天05:00到20:00每個整點時刻的溫度和輻照度數據，用后一時刻的輻照度測量值減去前一時刻的輻照度測量值的差值表示該時刻內的累計輻照度，并計算出每一時刻對應的太陽高度角。同時從網絡獲取以上六個月的天氣類型，進行分類[10]，見表1。

表1 廣義天氣類型

4種廣義的天氣類型在這6個月中的分布見表2。

表2 廣義天氣類型分布

由表2可以看出，在這6個月中A、B兩類天氣占大多數，C、D兩類天氣所占比例不到25%，因此在本研究中A、B兩類天氣的輻照度預測準確度為主要研究對象。

用第二部分的模型對輻照度進行訓練和預測。A、B類天氣的預測結果如圖5。

圖5 A、B類天氣預測結果對比圖

圖中帶圓圈的實線是每一時刻輻照度的實際測量值，帶點的虛線為僅通過歷史輻照度數據得到的預測結果，帶三角的虛線為該文提出的模型得到的輻照度預測結果。由圖可以看出，僅通過歷史輻照度數據預測的輻照度與實際值有較大的偏差，其中12月18日的正午時段預測曲線與原始數據的曲線趨勢明顯不符，預測失效。本文模型雖利用最易于獲取的氣象數據——環境溫度，但是得到的預測結果與實際值保持相同的變化趨勢，且每一時刻的預測值與實際值基本吻合，總體貼合程度較理想，這在一定程度上表明加入了環境溫度這一氣象數據比只用歷史輻照度數據進行預測準確性提高。

本文模型得到的預測值與實際值的相關性散點圖如圖6。

圖6 預測值與實際值的相關性散點圖

圖中可以看出，通過本文提出的模型得到的預測值與實際值相關性點都在y=x的直線附近，即相關性接近1，表明本文模型得出的預測值與實際值的相關性非常大。

為了進一步通過數據來說明該算法的可行性，下面將該算法與持續性方法(persistence method，以下簡稱PM)得到的均方根誤差(RMSE)進行對比分析。

PM是一種最早也是最簡單的預測算法，依賴于經驗值，也就是已經獲取的信息。該算法假設下一時刻的值與上一時刻相同，也就是用當前值作為下一時刻的預測值。該算法原理簡單操作簡便，常作為一個基準，來計算其他算法的預測技能skill，計算公式為：

(13)

其中：Es為本文算法的均方根誤差，Ep為PM的均方根誤差，skill為本文算法的預測技能。而均方根誤差(RMSE)的計算公式為：

(14)

其中：Bi(i=1,2,…m)為真實值，bi(i=1,2,…m)為預測值。

skill的值越接近1說明該算法與PM相比預測性能越好。一般情況下，skill值在0.8左右時是最理想也是最現實的狀態，此時該算法有一定的工程應用價值。

A、B類天氣預測值與實際值的均方根誤差(RMSE)以及skill值見表3。

表3 A、B類天氣預測技能

由表3可以看出12月16日到19日四天的skill值均在0.8以上，表明該算法在A、B類天氣時可以很好的對輻照度進行預測。

用上面的預測方法對C、D類天氣的輻照度進行預測，效果不是很理想，因此將這兩類天氣單獨提出，單獨訓練，同時通過改變隱含層數量，最終得到適合C、D類天氣輻照度預測的各項參數值，結果如圖7。

圖7 C、D類天氣預測結果

圖7中帶圓圈的實線為輻照度的實際測量值，帶三角的虛線為本文算法得到的輻照度預測值。從圖中可以看到，C、D類天氣預測結果偏差略大。究其原因，主要為雨雪天氣云層變化較為復雜，到達地面的太陽輻射瞬息萬變，因此導致這類天氣的輻照度預測準確性低，但從預測結果曲線可以看出，預測值與實際測量值的變化趨勢基本保持一致，且峰值基本上出現在相同的時刻，因此C、D類天氣時用該算法得到的預測值有一定的參考價值。C、D類天氣預測值與實際值的RMSE以及skill值見表4。

表4 C、D類天氣預測技能

從表4可以看出，在C、D類天氣時skill值均在0.5以上。由于A、B類天氣在該研究中所占的天數比重超過百分之七十五，因此為本文主要研究對象，由以上預測曲線和表格數據可以看出該模型在A、B類天氣時具有良的預測效果，與PM相比均方根誤差大幅度減小，同時skill值基本在0.8～0.85之間；在大雨雪天時預測值與實際測量值有一定的誤差，但整體趨勢保持一致，且skill值均在0.5以上。因此該優化模型在綜合考慮實測溫度數據和太陽高度角，且沒有考慮云量等復雜氣象信息的條件下可以較好地預測05:00到20:00時每小時輻照度，在實際的預測中，歷史輻照度值可以從數據庫中調取，溫度數據根據設備所在地區相應氣象站的天氣預報信息即可，不同時刻的太陽高度角根據第一小節的公式計算得出。

4 結論

本文運用多變量BP神經網絡算法根據武漢市特有的地理位置特點，將天氣類型進行分類，通過便于獲取的實測溫度數據和歷史輻照度數據，結合不同時刻的太陽高度角來對05:00到20:00時每小時輻照度進行預測。對得到的最終預測結果的分析可知，采用該模型對每小時輻照度進行預測時，A、B類天氣skill值在0.80～0.85之間，預測效果良好；若天氣情況復雜，由于云層變化迅速且很難預測，則導致預測結果與實際值之間有一定的誤差，但整體趨勢一致。考慮到本研究階段A、B類天氣所占比重大，對此兩類天氣情況下輻照度的預測精度高，算法的輸入變量獲取便捷，算法簡單，因此該模型可以較好的應用于光伏系統中輻照度的預測。

[1] 胥 芳，張 任，吳樂彬，等.自適應BP神經網絡在光伏MPPT中的應用[J].太陽能學報，2012，33(3)：468-472.

[2] Amrouche B，Pivert X L. Artificial neural network based daily local forecasting for global solar radiation[J]. Applied Energy，2014，130(5)：333-341.

[3] Besharat F，Dehghan A A，Faghih A R. Empirical models for estimating global solar radiation: A review and case study[J]. Renewable & Sustainable Energy Reviews，2013，21(21)：798-821.

[4] Zhou H，Sun W， Liu D，et al. The Research of Daily Total Solar-Radiation and Prediction Method of Photovoltaic Generation Based on Wavelet-Neural Network[A]. Asia-Pacific Power and Energy Engineering Conference[C]. IEEE Computer Society，2011：1-5.

[5] Zhang P，Takano H，Murata J. Daily solar radiation prediction based on wavelet analysis[A]. Sice Conference[C]. 2011：712-717.

[6] Mohammadi K，Shamshirband S，Tong C W，et al. A new hybrid support vector machine-wavelet transform approach for estimation of horizontal global solar radiation[J]. Energy Conversion & Management，2015，92(3)：162-171.

[7] Wang S，Liu C，Li Q. On the use of niching genetic algorithms for variable selection in solar radiation estimation[J]. Renewable Energy，2013，50(3)：168-176.

[8] 錢允祺. 關于任意緯度太陽高度角的查算[J]. 氣象，1978(10)：31-33.

[9] 王 飛，米增強，楊奇遜，等. 基于神經網絡與關聯數據的光伏電站發電功率預測方法[J]. 太陽能學報，2012，33(7)：1171-1177.

[10] 米增強, 王 飛, 楊 光,等. 光伏電站輻照度ANN預測及其兩維變尺度修正方法[J]. 太陽能學報, 2013, 34(2):251-259.

Reasearch on a Simple Short-term Forecast of Irradiation

Zhong Zhifeng1, Zhang Yi1, Zhang Tiantian1, Yang Chenxi1，Su Yong2

(1.School of Computer Science and Information Engineering, Hubei university, Wuhan 430062, China;2.School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China)

The precise prediction of irradiation is the critical factor of predicting the output power of photovoltaic power generation system, yet the irradiation vary from region to region because of the different latitude, weather types and altitude etc. Because complicated meteorological data in currently research about the forecast of short-term irradiation is hard to be collected, this paper proposes a simple method for short-term prediction of irradiance only using the meteorological data which easy to obtain. In consideration of the unique geographical location of Wuhan, the weather is classified to four types. The input variables are temperature, irradiance measured by real-time environmental monitoring and solar elevation angle at different times. Then the irradiation is calculated per hour from 05:00 to 20:00 using the multivariate backward feedback neural network model. Contrasting the result obtained from the model mentioned above and that only taking historical irradiation data as input, the former has a better outcome. At last, the forecasting skills is calculated based on the Persistence Method. The final results show that all the skills of the proposed model are greater than 0.75, almost distributed between 0.80 and 0.85 for the weather type A and B, which demonstrates the model proposed in this paper is capable of predicting short-term irradiation accurately based on the meteorological information which easy to be obtained.

forecast of short-term irradiation; solar elevation angle; BP neural network model; forecasting skills

2017-01-03；

2017-02-06。

鐘志峰(1971-)，男，湖北黃岡人，副教授，碩士研究生導師，主要從事雷達系統和信號處理以及光伏發電和系統集成等方向的研究。

張 藝(1992-)，女，河南安陽人，碩士研究生，主要從事信號處理及光伏發電方向的研究。

1671-4598(2017)07-0181-05

10.16526/j.cnki.11-4762/tp.2017.07.045

TP391.9

A