基于IMPSCO和改進Newmark-β算法的結構系統及激勵辨識研究

麻勝蘭， 姜紹飛， 陳志剛

(福州大學 土木工程學院，福州 350108)

基于IMPSCO和改進Newmark-β算法的結構系統及激勵辨識研究

麻勝蘭， 姜紹飛， 陳志剛

(福州大學 土木工程學院，福州 350108)

基于振動的土木工程結構系統識別中，常用的識別方法如基于Newmark-β算法的方法，常常需要已知激勵，而事實上激勵和完整的輸出響應是很難測得的。基于此，在現有的Newmark-β算法中引入多項式擬合來解決結構系統識別誤差帶來的漂移現象，進而提出了改進的Newmark-β算法，并結合改進協同粒子群算法(IMPSCO)，給出了僅用部分結構響應的系統識別和激勵辨識方法。最后，通過一七層鋼框架數值算例和實驗室模型試驗驗證了方法的有效性和可行性，并探討了噪聲、輸出響應完整性的影響。研究表明，所提方法能準確地實現未知激勵和部分實測響應狀態下的結構系統和未知激勵的識別，而且具有較強的容噪性和魯棒性。

未知激勵；系統識別；改進的Newmark-β算法

結構系統參數識別是結構健康監測的核心部分，因此國內外專家提出了很多系統識別方法[1-4]。其中，時域下基于結構振動響應的識別方法受到了廣泛關注，通過直接識別結構系統的物理參數，如剛度、質量或阻尼等，可以有效確定損傷位置、損傷程度和評估結構狀態。這些方法如最小二乘法(Least Square,LS)[5]、卡爾曼濾波(Kalman Filter,KF)[6]和遺傳算法(Genetic Algorithm,GA)[7]等。但分析發現，這些方法大多僅適用于輸入與輸出都已知的情形，而實際工程中，由于環境的復雜性，一般難以測得結構實際受到的激勵大小，甚至也難以測得完整的結構輸出響應。因此，研究未知激勵及部分實測輸出響應狀態下的結構系統辨識方法，意義重大。

國內外專家學者開展了一系列研究，取得了一定成果。Chen等[8]利用改進的迭代最小二乘法同時識別結構系統參數和未知輸入力；此后，Chen等[9]又提出利用蟻群算法同時識別結構系統參數和未知激勵，并通過試驗驗證了方法的有效性；此外，Sun等[10]將改進Newmark-β算法與人工蜂群算法結合，來同時識別未知激勵及結構系統參數。但研究發現Chen的方法并不適用于僅有部分實測響應的情形；而Sun的方法通過將加速度積分成速度和位移，進而根據動力方程求得未知激勵，但實際工程中，加速度積分會由于“平移項”和“趨勢項”的影響[11]使速度、位移和識別激勵發生漂移，導致識別錯誤。

因此，本文的目的在于研究一種未知激勵及部分實測響應下，能同時識別激勵與結構系統參數的時域下的辨識策略。時域下的結構系統識別通常需要與各種數值積分方法相結合，其中最常用的數值方法為Newmark-β算法[12-13]，但是常規Newmark-β算法需要已知激勵，為此，通常做法是通過易測得的加速度積分得到速度和位移響應，再根據結構動力方程求得激勵，然后進行系統參數識別。但如上所述，加速度積分存在趨勢項誤差，會使速度、位移和識別激勵發生漂移，并導致系統參數識別錯誤。鑒于此，本文借鑒多項式去趨勢的思想，對常規Newmark-β算法進行改進，利用多項式擬合來修正加速度積分導致的識別激勵的漂移現象；在此基礎上，結合改進協同粒子群算法(IMPSCO)，提出了一種適用于未知激勵及部分實測響應下的結構系統參數識別與激勵辨識方法，并通過一7層框架數值仿真和試驗研究驗證了方法的有效性和可行性。

1 改進的Newmark-β算法

本文對Newmark-β算法進行了改進，具體步驟如下：

步驟1 初始計算加速度、速度、位移和力：

①確定結構的質量、阻尼和剛度矩陣M,C,K,及時間步長Δt；

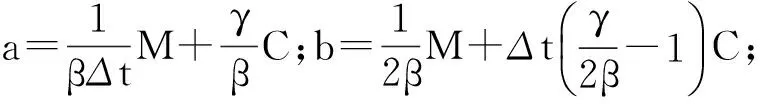
步驟2 由每個時間步p計算第p+1個時間步的結構響應和激勵：

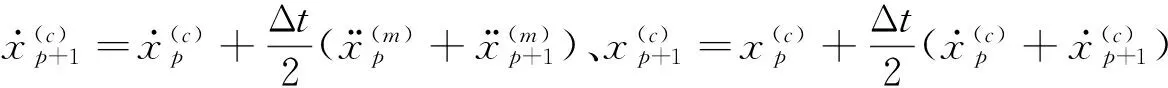
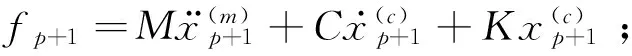
③按照傳統Newmark-β算法計算結構響應：

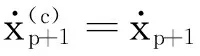
步驟3 對下一個時間步進行循環令p=p+1，重復步驟2中的①～④；

步驟6 識別激勵修正：fiden=f-ffit。

步驟7 將fiden作為已知激勵，并重復執行步驟2中的③步驟直到所有時間步循環結束。

總體而言，改進的目的在于解決以下兩個問題：

(1) 激勵未知下，程序的執行問題及未知激勵的識別；

(2) 修正可能發生的識別激勵的漂移現象。對于前者，本文借鑒Sun的方法，利用已知的實測加速度積分成速度和位移，進而根據動力方程求得未知激勵。然而，Sun在計算下一時間步的速度響應時采用的上一時間步得到的速度和位移經常規Newmark-β算法公式(類似本文所提算法步驟步驟2步驟中的①～③)計算得到的數值加速度，這無疑會增加計算誤差，因而本文將其改用為實測加速度(步驟2步驟中的①～②)；此外，本文在計算中加入了識別激勵的更新(步驟2步驟中的④)，以進一步減少可能存在的由于積分引起的識別誤差。對于后者，本文利用多項式擬合去除可能發生的激勵漂移現象，得到修正的識別激勵，并將其作為已知值重新計算結構響應(步驟5～8)。

2 系統識別與激勵辨識策略

如上所述，本文將IMPSCO與改進Newmark-β算法結合起來，提出了一種適用于未知激勵及部分實測響應狀態下的結構系統識別與激勵辨識策略，其流程如圖1所示；IMPSCO是對MPSCO的改進，通過對局部最優粒子的替換處理，提高了算法的穩定性和魯棒性，具體過程可詳見文獻[14]。此外，考慮到加速度相較容易獲得，本文基于加速度響應進行研究。因此，在激勵位置、激勵部位及其相鄰部位加速度已知時，即可利用本策略識別結構系統參數和未知激勵。具體步驟如下：

(1) 對結構系統參數進行編碼并確定參數搜索范圍，本文考慮質量已知情形，對于阻尼，則采用Rayleigh阻尼模型，因此需要編碼的結構系統參數θ為剛度ki(i=1,2,…,n)和阻尼比ξj(j=1,2)；

(2) 設置IMPSCO的基本算法參數，本文設置如下：子種群數量為Ns=3；子種群大小為ms=30；進化代數me=500；學習因子c1=c2=2；最差次數限值Ie=6；w=[0.4,0.9]，線性遞減，且當迭代次數大于45時，取0.4；

(3) 在各參數搜索范圍內隨機產生若干隨機粒子(即不同參數值的組合)，并按第一節，利用改進Newmark-β算法計算每個隨機粒子下的結構響應及未知激勵(fiden)；

(4) 以實測加速度響應和計算所得加速度響應為基礎建立適應度函數F，如式(1)所示，并計算每個隨機粒子的適應度值；

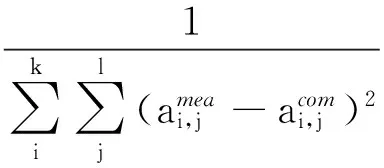
(1)

式中，amea和acom分別為結構實測加速度響應和數值計算的加速度響應;k是結構測點數;l為加速度響應數據的個數。適應度計算值越大，識別結果越接近實際值。

(5) 替換掉適應度值最差的粒子，并對每個粒子按IMPSCO的設定進行粒子進化；

(6) 同樣按第一節，利用改進Newmark-β算法計算每個進化粒子組合下的結構響應及未知激勵(fiden)，并重復步驟(4)和(5)；

(7) 重復步驟(6)，進行粒子循環迭代進化，直到達到設定的最大迭代次數，迭代結束，輸出適應度值最高的粒子，即最優系統參數和未知激勵(fiden)。

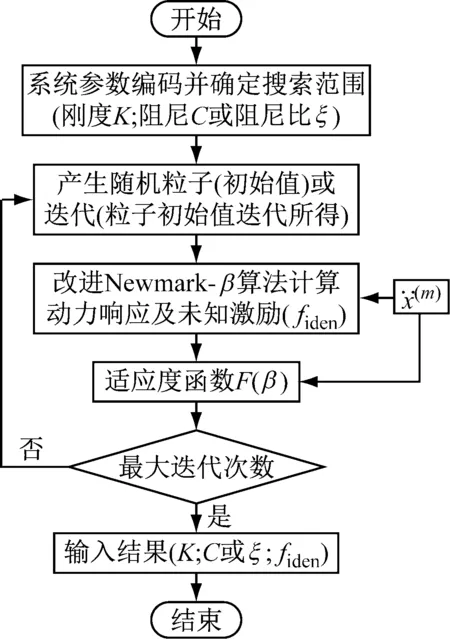
圖1 結構系統識別與激勵辨識策略流程圖

3 數值算例

3.1 結構模型

圖2為一7層剪切型框架結構，剛度為k1=…=k7=375 kN/m;質量為m1=…=m6=3.78 kg和m7=3.31 kg;采用Rayleigh阻尼模型，前兩階阻尼比為ξ1=ξ2=2%。頂層受隨機激勵，采用常規Newmark-β算法計算結構動力響應，并取加速度響應用于分析，采樣頻率1 000 Hz，采樣時間5 s。

3.2 識別過程與結果

本例中，質量已知，以結構各層層間剛度及阻尼比為未知，進行編碼識別，即θ=[k1,k2,…,k7,ξ1,ξ2]。參數搜索范圍取理論值的0.5倍～2倍，即ki∈[187.5,700]kN/m,i=1,2,…,7;ξj∈[0.01,0.04],j=1,2。按圖1流程，識別結構參數θ及未知激勵fiden，改進Newmark-β算法中多項式擬合階數取n=4。識別時，僅考慮第2,3及5～7層加速度響應以模擬響應不完整情形。無噪聲下，阻尼比的識別值分別為2.05%和2.09%，結果較為精確；剛度識別結果如表2所示；激勵識別結果如圖3所示，為簡便，圖中僅給出0～0.5 s識別結果。

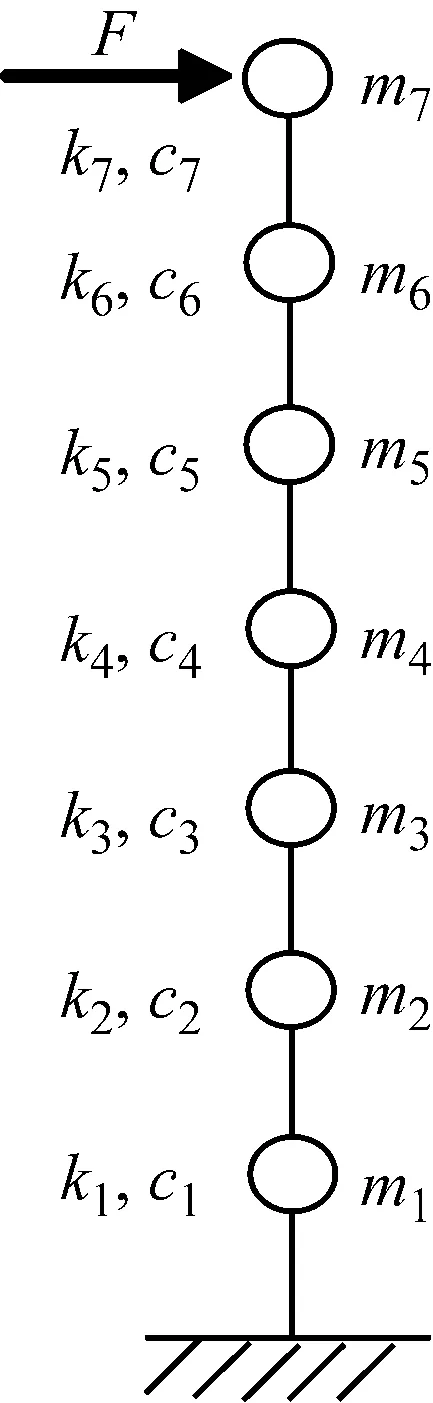
圖2 結構模型

從表2可以發現，結構剛度的識別結果與理論值非常接近，最大誤差僅為0.20%；而從圖3(a)可以發現，激勵的識別值也與理論值非常吻合。此外，圖4為未經多項式修正時的激勵識別結果(即識別過程沒有加入第一節中步驟5～8)，可以發現即使未利用多項式進行修正時，識別激勵也沒有明顯發生漂移，這是由于本例為數值算例，在正向計算結構數值響應與反向識別結構物理參數時，實際上都是基于Newmark-β算法的基本假設進行的，因此識別中不會出現明顯的激勵漂移現象，因此，識別時多項式的修正值為0，但實際工程中，結構響應是實際測得的，并不完全滿足這一假設，因而容易產生趨勢誤差，導致識別激勵發生漂移，這將在下一節試驗中得到驗證。以上分析表明，無噪聲下，本文所提策略可以精確識別結構系統參數和未知激勵。

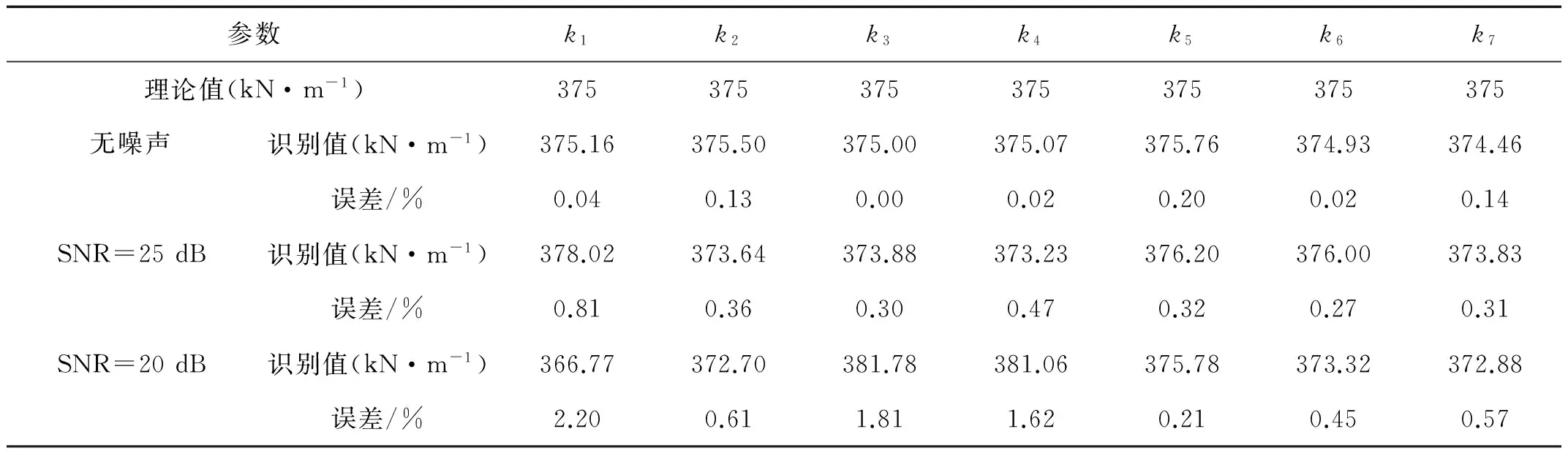
表2 剛度識別結果

(a) 無噪聲

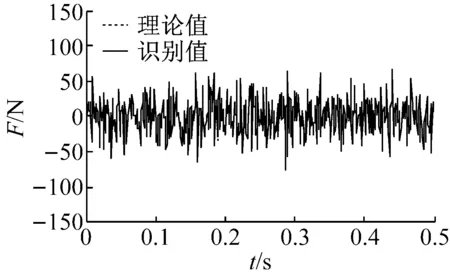
(b) SNR=20 dB

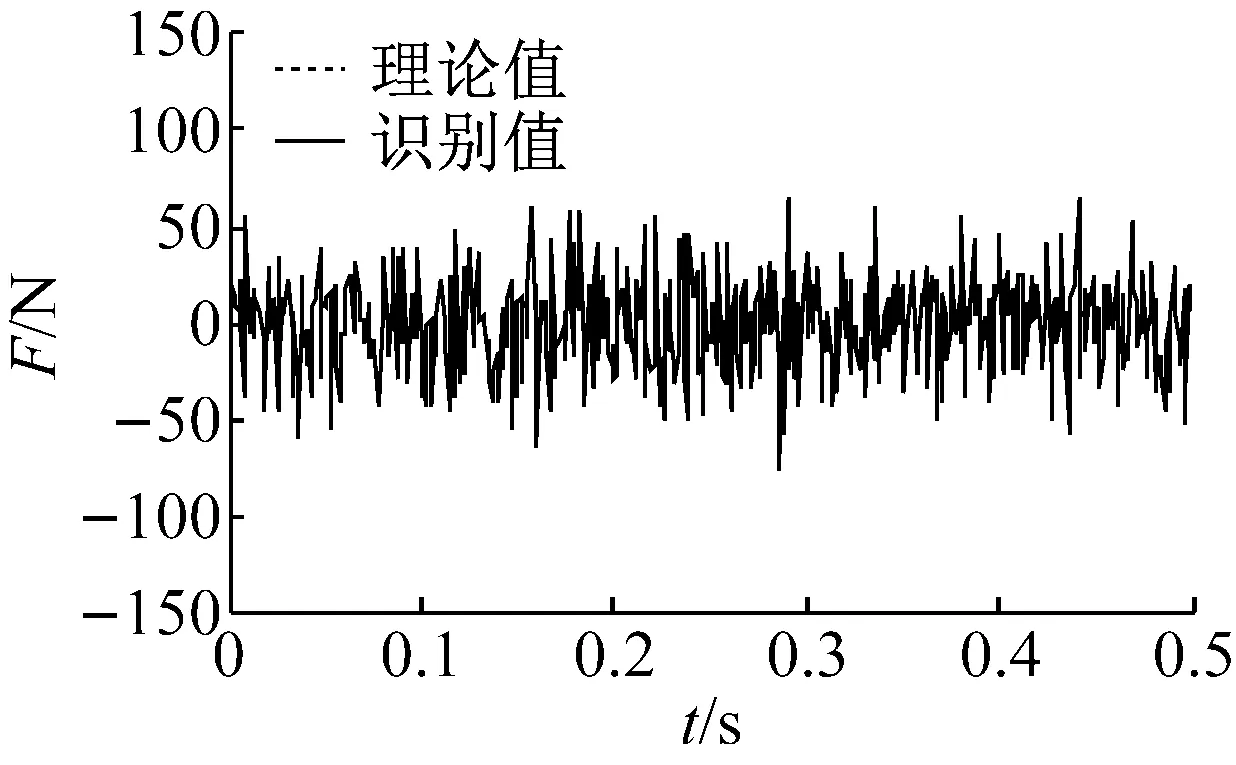
圖4 未修正下激勵識別結果

3.3 比較與討論

為驗證本文方法的適用性和魯棒性，從噪聲水平和輸出響應的完整性兩個方面進行分析討論。

(1) 噪聲影響

按式(2)向原始加速度響應中添加噪聲，信噪比(SNR)分別為25 dB和20 dB。

SNR=20lg(1/ε)=20lg(Asignal/Anoise)

(2)

式中:yia和yi分別代表原始位移響應信號和噪聲污染后的信號;R是均值為0，偏差為1的正態分布隨機數;ε為噪聲水平;A為信號幅值。

同樣，按圖1流程進行識別, 剛度和激勵的識別結果如表2和圖3所示。可以看出，SNR=25 dB和20 dB時，剛度的最大識別誤差也僅為0.81%和2.20%，而激勵的識別結果也仍然非常精確。此外，SNR=25 dB時，阻尼比的識別值分別為2.12%和2.17%；SNR=20 dB時，則分別為2.24%和2.25%；實質上Rayleigh阻尼比為2%。可見阻尼比的識別誤差與剛度識別一致，隨噪聲增加，其中阻尼比誤差更大一些，這是由于本例為小阻尼結構，阻尼對系統響應影響較小所致，但總體上其誤差尚在可接受范圍內。這些表明，本文所提策略具有較好的容噪性和魯棒性。

(2) 輸出響應的完整性

為驗證輸出完整性對本文方法的影響，無噪聲下，分別利用第5～7層、第2,3,5～7層和第1～7層的加速度響應進行識別。剛度和激勵識別結果如表3和圖5所示。

1～7層加速度都參與識別時，阻尼比分別為2.08%和2.02%，最大誤差4.00%，而僅有5～7層的加速度響應參與識別時，其值分別為2.19%和2.25%，最大誤差為12.50%。可見參與識別的加速度響應個數對于阻尼比的識別影響較大，但從表3可以發現，其對剛度的識別影響較小。當只有5～7層的加速度響應參與識別時，剛度的最大識別誤差也僅增大到0.74%，激勵的識別結果也仍然非常精確(圖6(b))。這些表明，雖然加速度響應的完整性會影響參數及激勵識別結果，但影響較小，本文策略仍具有較高識別精度。

表3 不同測點組合下的辨識結果

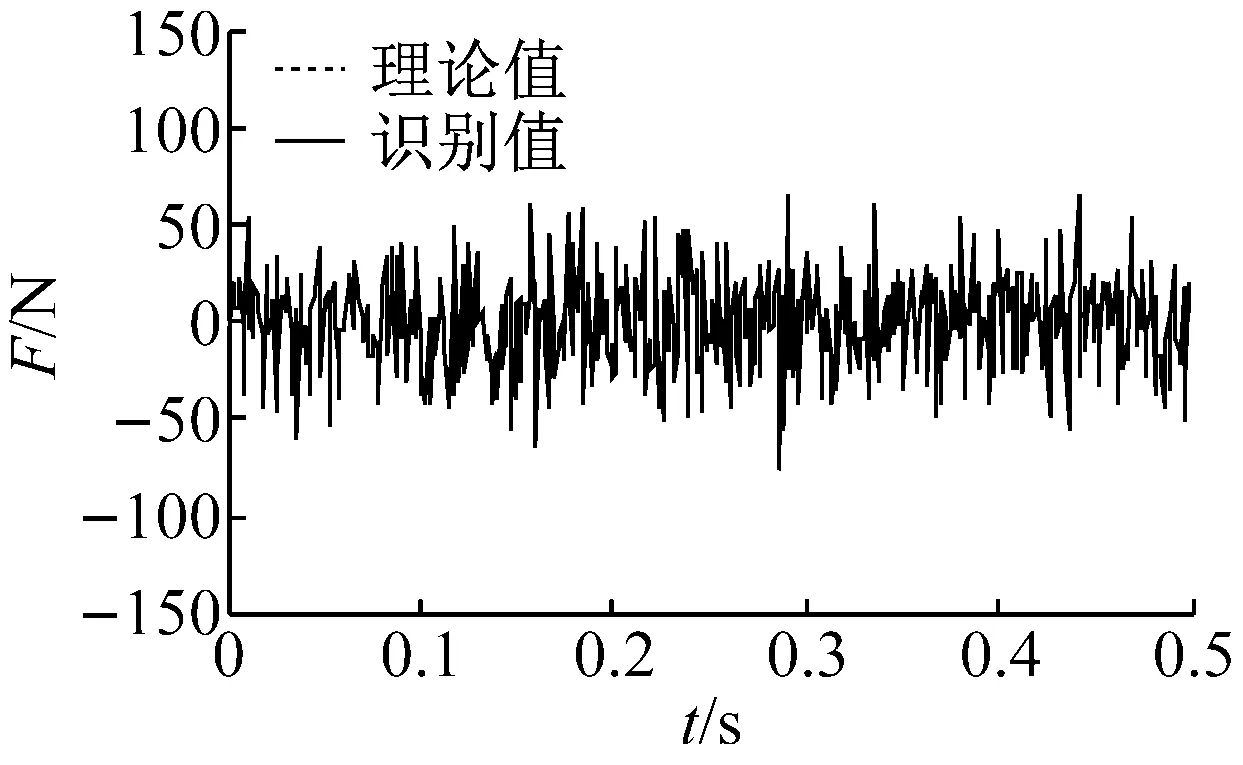
(a) 第1～7層

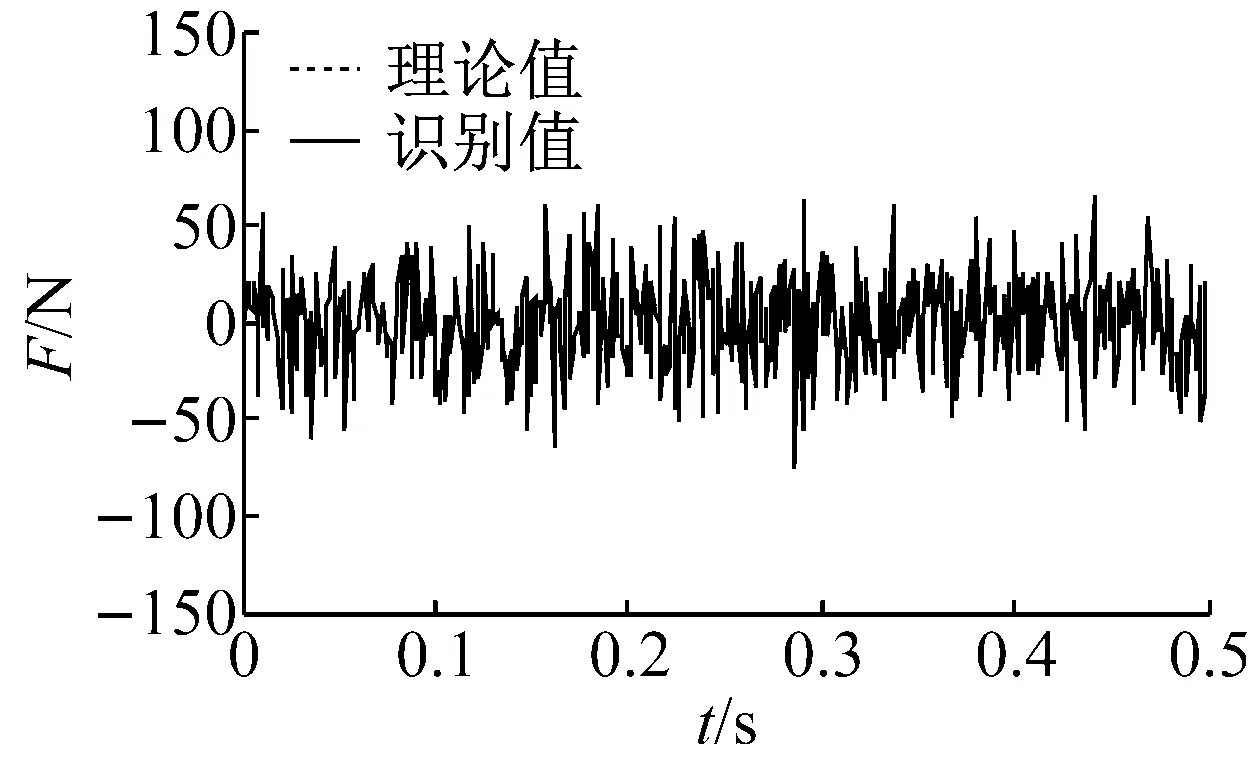
(b) 第5～7層

4 試驗驗證

4.1 試驗模型

如圖6所示，為2跨×1跨的7層鋼框架縮尺模型，相應的數學簡化模型如圖2所示。梁、柱間距均為200 mm。梁為空鋼管，柱為薄鋼板，且均為300 W級鋼材。構件特性如表4所示,據此可求得結構各層質量為m1=m2=…=m6=3.78 kg，m7=3.31 kg，完整狀態下結構各層理論剛度均為375 kN/m。利用激振器在結構頂層施加隨機激勵，并利用力傳感器記錄激振力大小，采樣頻率5 000 Hz。在結構各層布置傳感器以測量各層加速度響應。

圖6 實驗室鋼框架模型

參數梁柱截面尺寸/mm25×25×325×4.6截面面積A/m2286×10-6115×10-6慣性矩I/m42.41×10-87.78×10-10楊氏模量E/Pa206×109206×109體密度ρ/(kg·m-3)78507850

4.2 結構系統修正

利用結構剛度理論值計算出結構的理論頻率并與試驗中測得實測頻率進行對比，如表5所示。

表5 結構固有頻率

從表5可以看出，理論頻率與實測頻率偏差較大，可見理論剛度值不符合結構實際條件，這是由于試驗材料自身的缺陷、焊接的影響、試驗設備的測量誤差、試驗人員人為的因素及測量時噪聲的影響等多種因素引起的，因此需要對其進行修正。

為此，在激勵已知下，利用IMPSCO進行剛度識別與修正。首先對結構各層層間剛度及阻尼比進行編碼，即θ=[k1,k2,…,k7,ξ1,ξ2]。參數搜索范圍為ki∈[187.5,700]kN/m,i=1,2,…,7;ξj∈[0,1],j=1,2。剛度的識別結果如表6所示。而后利用識別剛度計算結構的固有頻率，如表5所示，可以看出，識別頻率與實測頻率更加吻合，從而表明識別的剛度值更符合實際結構狀況。因此，后文分析時以此剛度識別值作為激勵未知下的剛度基準值，以便對比。

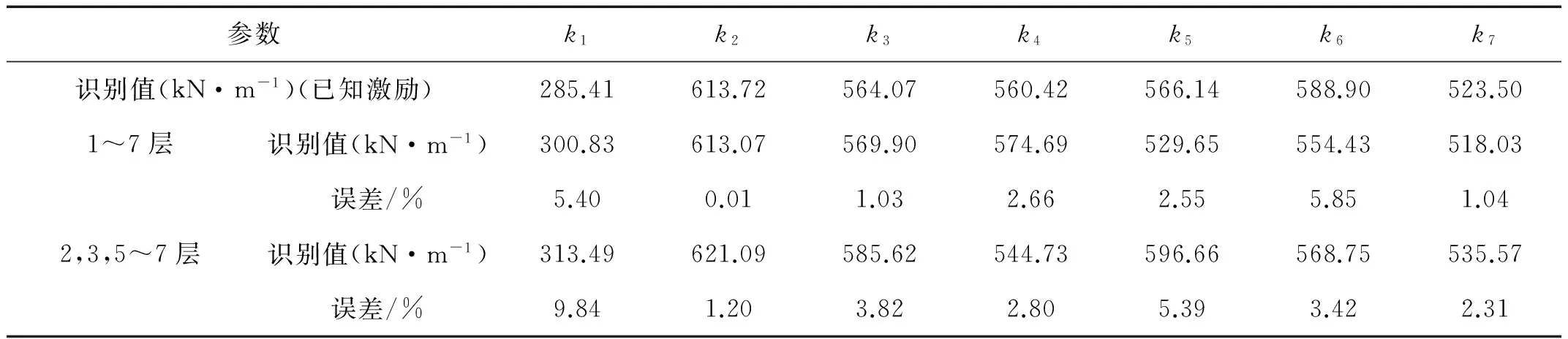
表6 不同測點組合下的剛度識別結果

4.3 識別過程與結果

以第2，3及5～7層的加速度響應作為已知輸出響應，以模擬響應不完整情形，對各層剛度及阻尼比進行編碼，搜索范圍與4.2節一致，并按圖1流程進行識別，多項式階數同樣取n=4。阻尼比的識別結果分別為0.68%和2.02%；剛度和激勵的結果分別如表6和圖7(b)所示。圖7(a)為未經多項式修正時的激勵識別結果(第一節中步驟5～8步)。

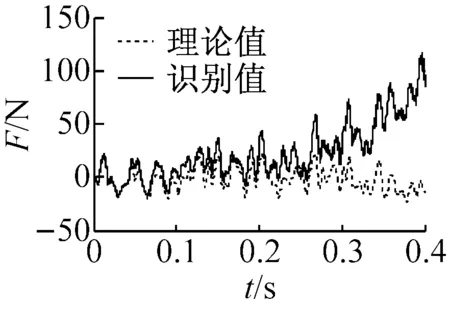
(a) 未修正(不完整響應,第2,3,5～7層加速度)

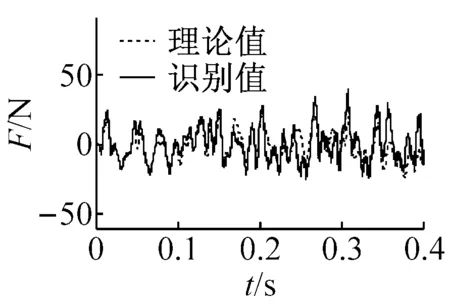
(b) 修正(不完整響應,第2,3,5～7層加速度)

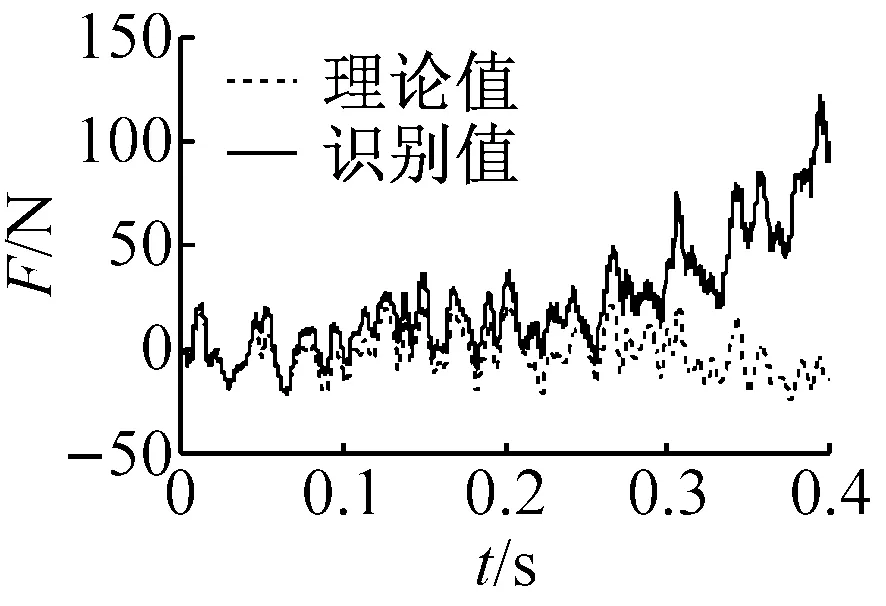
(c) 未修正(完整響應,第1～7層加速度)

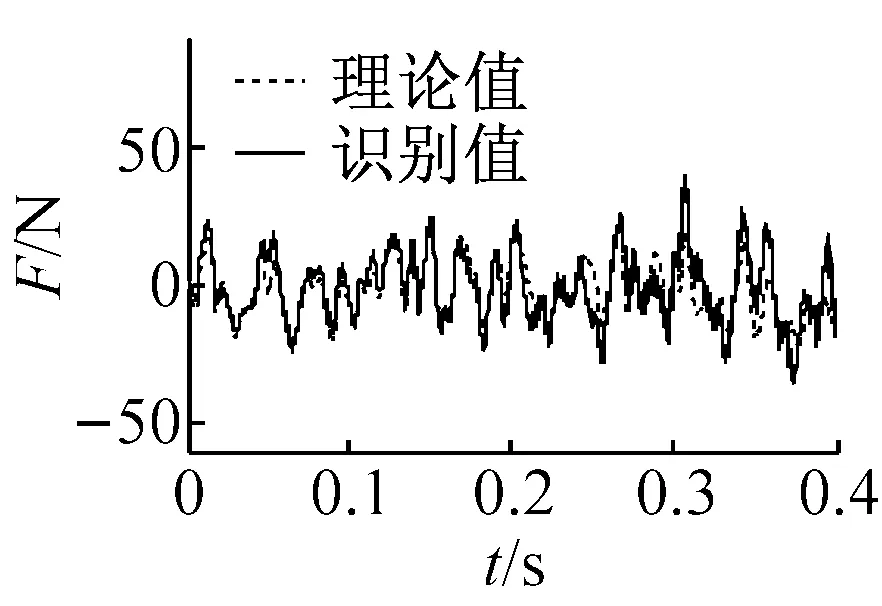
(d) 修正(完整響應,第1～7層加速度)

圖7 激勵識別結果

Fig.7 The identified results of excitation

從表6可以看出，激勵未知下，剛度的識別結果與激勵已知時的識別結果較為接近,最大誤差僅為9.84%；此外，從圖7(a)可以發現，識別激勵由于加速度積分的趨勢誤差發生了明顯漂移；但經本文所提策略修正后，激勵的識別結果明顯沒有了漂移現象，且與實測值較為吻合，如圖7(b)所示。以上分析表明，本文策略可以有效識別結構系統參數和未知激勵，并消除激勵的漂移現象。

4.4 比較與討論

為了驗證本文方法的魯棒性和有效性，對同樣的結構模型進行了激勵未知及完整響應狀態(7層加速度都已知)下的系統辨識。首先對結構各層層間剛度及阻尼比進行編碼，參數搜索范圍與4.2節一致，同樣按圖2流程進行識別，多項式擬合階數同樣取n=4。阻尼比的識別值分別為0.52%和1.86%，與4.3節的識別結果較為接近，且都比較小；剛度和激勵的結果如表6和圖7(d)所示，圖7(c)同樣為未經多項式修正時的激勵識別結果。

從表6可以發現，相較完整輸出響應情形，僅有部分實測響應時，剛度的最大誤差從5.85%增加到9.84%，可見識別誤差雖有所增大，但仍有較高的識別精度；此外，從圖7(b)和圖7(d)對比發現，相較完整輸出響應情形，部分實測響應下激勵識別值與激勵實測值的吻合度雖有所不如，但總體上仍然較為吻合。以上對比表明，雖然加速度響應的不完整性對參數和激勵的識別有所影響，但本文所提策略仍表現出較高的識別精度和魯棒性，能滿足工程需要。

5 結 論

本文通過研究，得出了以下結論：

(1) 通過改進常規Newmark-β算法并結合IMPSCO，提出了系統辨識策略，有效解決了僅有部分實測輸出響應下的結構系統識別和激勵辨識問題。

(2) 響應完整性確會影響識別結果，但本文策略對于僅有部分實測輸出響應下的系統參數識別仍具有較高的識別精度和較強的魯棒性。

(3) 研究表明，所提改進Newmark-β算法確實能有效消除識別激勵的漂移現象，保證了系統識別結果的準確性。

數值模擬和試驗研究表明，所提策略能有效識別結構系統參數和激勵，初步驗證了該方法的可行性和有效性，且具有較好的容噪性，但仍需要更多的試驗和工程實踐來進一步檢驗。此外，本文策略僅適用于激勵位置已知的情形，對于激勵位置未知情形，還有待進一步研究和擴展。

[1] 張延年, 范鶴, 董錦坤. 基礎隔震結構的系統參數優化設計[J]. 沈陽建筑大學學報, 2006,22(4):529-533.

ZHANG Yannian, FAN He, DONG Jinkun. Parameter optimization of base-isolated structure[J]. Journal of Shenyang Construction University, 2006,22(4):529-533.

[2] TANG H, ZHANG W, XIE L, et al. Multi-stage approach for structural damage identification using particle swarm optimization[J]. Smart Structures and Systems, 2013, 11(1): 69-86.

[3] WANG F G, LING X Z, XU X, et al. Structural stiffness identification based on the extended kalman filter research[J].Abstract and Applied Analysis, 2014(2):267-290.

[4] YANG J N, HUANG H, LIN S. Sequential non-linear least-square estimation for damage identification of structures[J]. International Journal of Non-Linear Mechanics, 2006, 41(1):124-140.

[5] LIN J W, BETTI R, SMYTH A W, et al. On-line identification of non-linear hysteretic structural systems using a variable trace approach[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(9):1279-1303.

[6] HOSHIYA M, SAITO E. Structural identification by extended Kalman filter[J]. Journal of Engineering Mechanics, 1984,

110 (12):1757-1770.

[7] PERRY M J, KOH C G, CHOO Y S. Modified genetic algorithm strategy for structural identification[J]. Computers & Structures, 2006, 84(8/9):529-540.

[8] CHEN J, LI J. Simultaneous identification of structural parameters and input time history from output-only measurements[J]. Computational Mechanics, 2004, 33(5): 365-374.

[9] CHEN J, CHEN X, LIU W.Complete inverse method using ant colony optimization algorithm for structural parameters and excitation identification from output only measurements[J]. Mathematical Problems in Engineering, 2014, 18(1):249-269.

[10] SUN H, BETTI R. Simultaneous identification of structural parameters and dynamic input with incomplete output-only measurements[J]. Structural Control and Health Monitoring, 2014, 21: 868-889.

[11] JUNHEE K, KIYOUNG K, HOON S. Autonomous dynamic displacement estimation from data fusion of acceleration and intermittent displacement measurements[J]. Mechanical Systems and Signal Processing, 2014,42(1/2):194-205.

[12] MAUNG T S, CHEN H P, ALANI A M. Real time structural damage assessment from vibration measurements[J]. Journal of Physics: Conference Series, 2011, 305(1):12096-12103.

[13] SHIN S B, OH S H. Damage assessment of shear buildings by synchronous estimation of stiffness and damping using measured acceleration[J]. Smart Structures and Systems, 2007, 3(3):245-261.

[14] JIANG S F, WU S Y, DONG L Q.A time-domain structural damage detection method based on improved multi-particle swarm coevolution optimization algorithm[J].Mathematical Problems in Engineering, 2014, 44(1):77-85．

Identification of a structural system and its excitation based on IMPSCO and modified Newmark-βalgorithm

MA Shenglan, JIANG Shaofei, CHEN Zhigang

(College of Civil Engineering, Fuzhou University, Fuzhou 350108, China)

In vibration-based structural system identification (SI) of a civil structure, the commonly used SI method, such as, the one based on Newmark-βalgorithm usually needs the known excitation. In fact, it is difficult to measure the actual excitation and full output responses of a structure system. Here, a modified Newmark-βalgorithm was proposed through introducing polynomial fitting into Newmark-βalgorithm to effectively solve the drift phenomenon brought by the error of SI. Furthermore, combining the modified Newmark-βalgorithm with the improved multi-particle swarm co-evolution optimization (IMPSCO), an identification approach of SI and excitation adopting responses of parts of a structure system was presented. Finally, numerical simulation for a seven-story steel frame and its model tests were conducted to verify the effectiveness and feasibility of the proposed method. The effects of noise and completeness of structural response were also discussed. The results showed that the proposed method can be used to effectively identify a structural system and its excitation only adopting responses of parts of the structure system; it has stronger noise tolerance and robustness．

unknown excitation; system identification; modified Newmark-βalgorithm

國家十二五科技支撐計劃(2015BAK14B02)國家自然科學基金(51278127)

2015-09-22 修改稿收到日期：2016-06-28

麻勝蘭 女，博士,1986年生

姜紹飛 男,閩江學者特聘教授，博士，博士生導師,1969年生 E-mail：cejsf@fzu.edu.cn

TU317

A

10.13465/j.cnki.jvs.2017.15.004