雙電荷在勻強磁場中的運動軌跡①*
楊 潔
(湖州師范學院理學院 浙江 湖州 313000)
姜付錦
(武漢市黃陂一中 湖北 武漢 430300)
邱為鋼
(湖州師范學院物理視覺工作室 浙江 湖州 313000)

雙電荷在勻強磁場中的運動軌跡①*
楊 潔
(湖州師范學院理學院 浙江 湖州 313000)
姜付錦
(武漢市黃陂一中 湖北 武漢 430300)
邱為鋼
(湖州師范學院物理視覺工作室 浙江 湖州 313000)
給出了質量和電荷值相等的雙電荷在勻強磁場中的運動方程,討論了運動守恒量和軌跡特性;數值求解方程,給出了軌跡封閉時軌跡曲線.
雙電荷 勻強磁場 軌跡
點電荷在勻強電場和磁場中運動,隨著初始條件的不同,軌跡可以為拋物線、螺旋線、擺線等[1,2];作為推廣,我們考慮點電荷產生的電場和勻強磁場復合電磁場中點電荷的軌跡問題,分為三種模型.三種模型都是在起始時刻加上一個勻強磁場, 磁場垂直于點電荷運動平面. 第一種模型是一個負電荷固定,一個正電荷做勻速圓周運動,加上勻強磁場后正電荷的運動軌跡;第二個模型是自由異號雙電荷,起始靜止,在勻強磁場中的運動軌跡;第三個是自由同號雙電荷,起始靜止,在勻強磁場中的運動軌跡.
1 第一種模型對應的電荷運動軌跡
設固定電荷電荷量為-q,運動電荷為+q,質量為m,原先繞固定電荷做勻速圓周運動,半徑是L.以加入勻強磁場時刻記時,以固定電荷為原點,設運動電荷的位移為r,那么運動方程是
(1)
無論為了解析分析還是數值計算方便,要把以上方程量綱歸一化.設長度量綱是L,時間量綱是T0,磁場量綱是B0.式(1)中的3項量綱相等,都是力的量綱,得到
(2)
由此得到
采用極坐標,設磁場強度為B=kB0ez,其中k是磁場相對強度,即磁場強度與磁場量綱B0的比值.運動電荷位移為r=ρeρ.
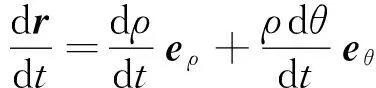
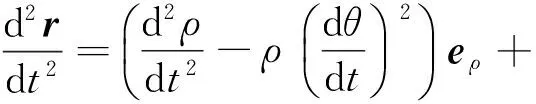
(3)
把以上各式代入式(1),得到量綱歸一化后的運動方程
(4)
(5)
(6)
(7)
這個守恒量其實就是量綱歸一化后的能量.式(6)中解出角速度的表達式,然后代入式(7),化簡得到
(8)
利用數學軟件分析發現,式(8)右邊有兩個實根,一個是ρ=1,還有一個就是矢徑極值.電荷從矢徑為1的地方運動到矢徑極值處,然后繼續運動到矢徑為1的地方,形成一個運動周期,這也為數值計算結果所驗證.但是周期轉動角不再是2π的有理數倍,一般不會返回到原處.
我們用數值求解式(4)和式(5)的方法來求軌跡.數值計算給出,當磁場相對強度k取適當值時,周期轉動角是2π的有理數倍,電荷的運動軌跡封閉且有對稱性.磁場正方向時,對稱封閉軌跡如圖1所示.
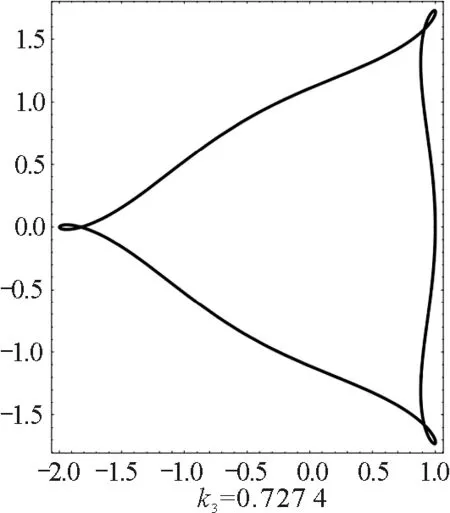
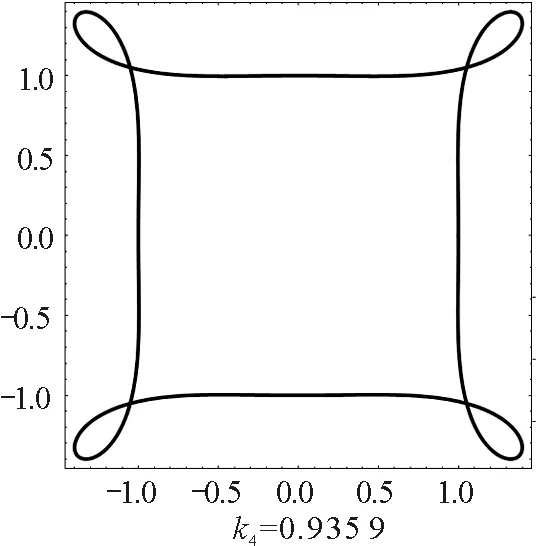
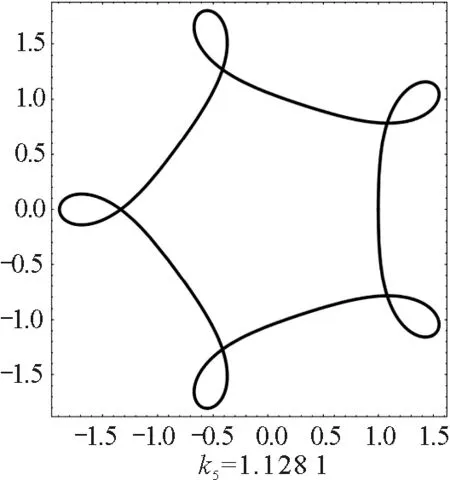
圖1 磁場正方向時正電荷的對稱封閉軌跡
磁場反方向時,對稱封閉軌跡如圖2所示.
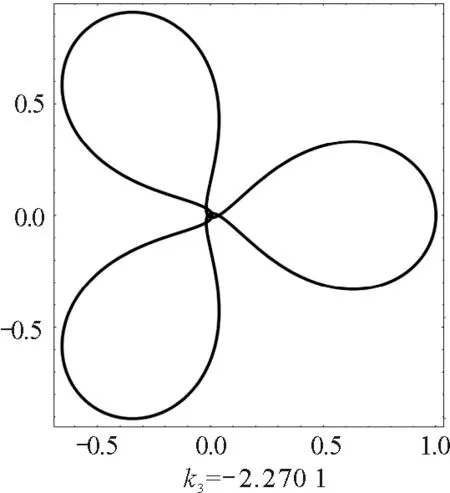
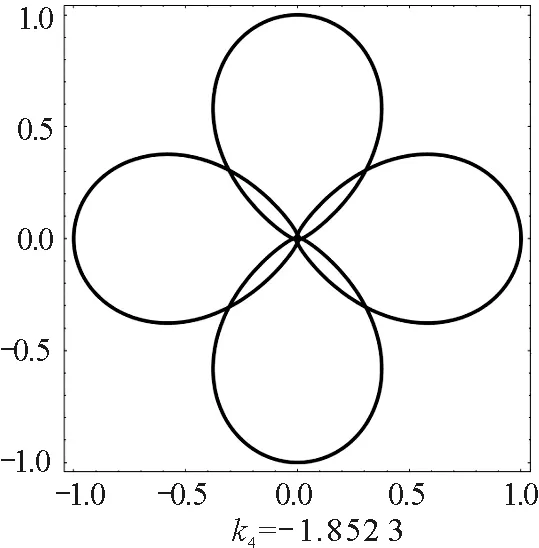
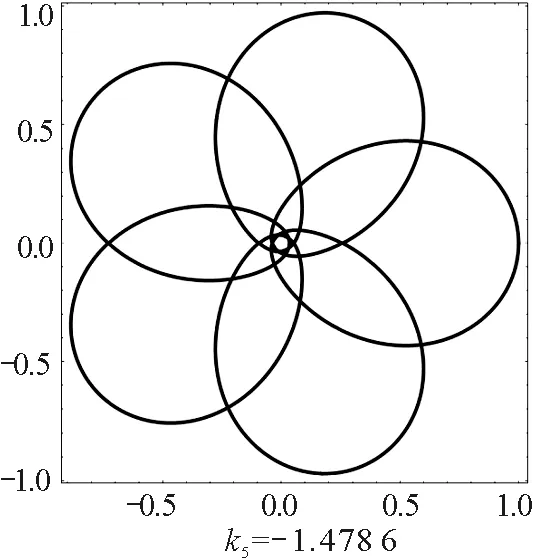
圖2 磁場反方向時正電荷的對稱封閉軌跡
2 第二種模型對應的電荷運動軌跡
設起始時候正電荷在坐標(1,0)處,負電荷在(-1,0)處,兩個電荷起始速度都為零.設正電荷的坐標是(x1,y1),負電荷的坐標是(x2,y2).由對稱性可知
x1(t)=-x2(t)=x(t)
y1(t)=y2(t)=y(t)
那么兩個電荷的量綱歸一化后的4個運動方程簡化為以下兩個方程
(9)
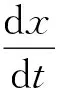
(10)
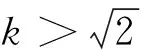
(11)
那么右邊正電荷在(xmin,1)區間做周期運動.
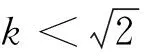
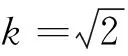
當磁場相對強度k分別等于0.6,0.9,1.2時,兩個電荷的運動軌跡如圖3所示.
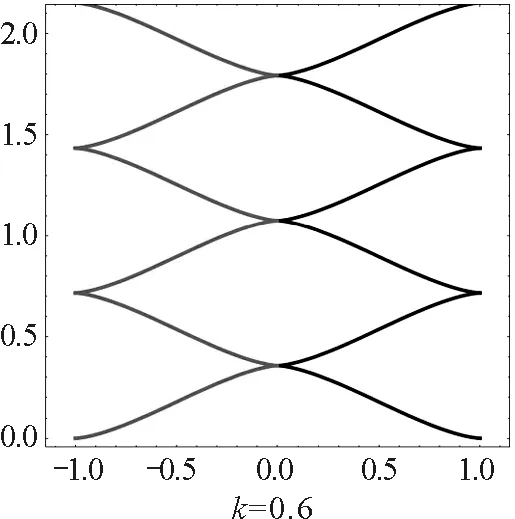
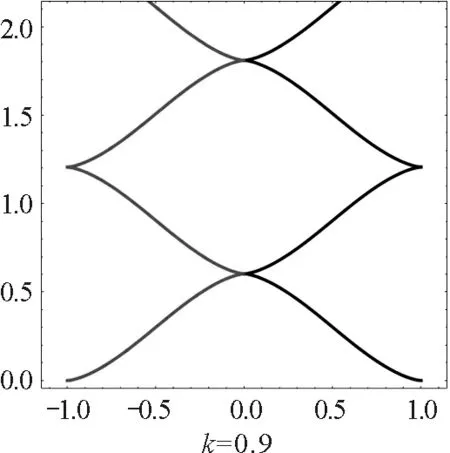
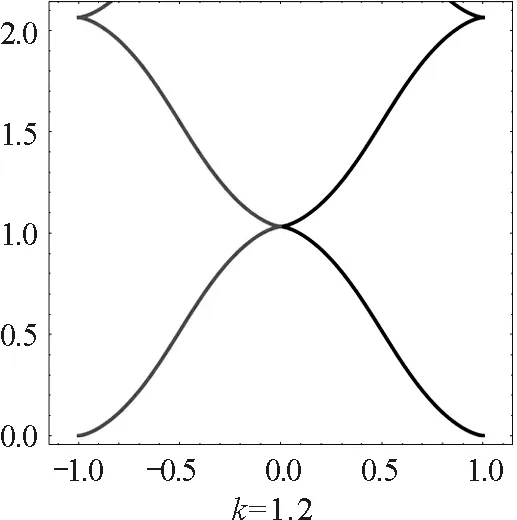
圖3 小于臨界值時不同相對強度磁場下的異號雙電荷軌跡
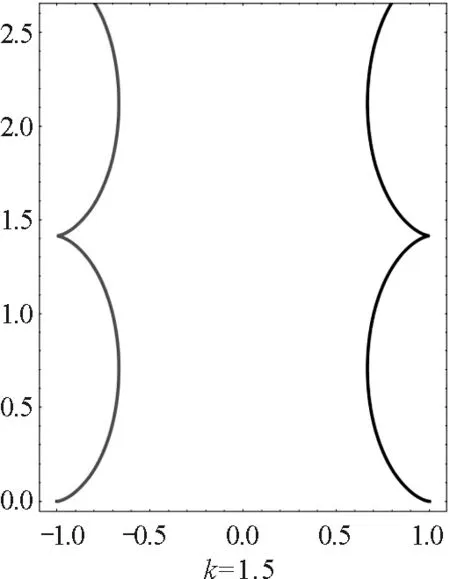
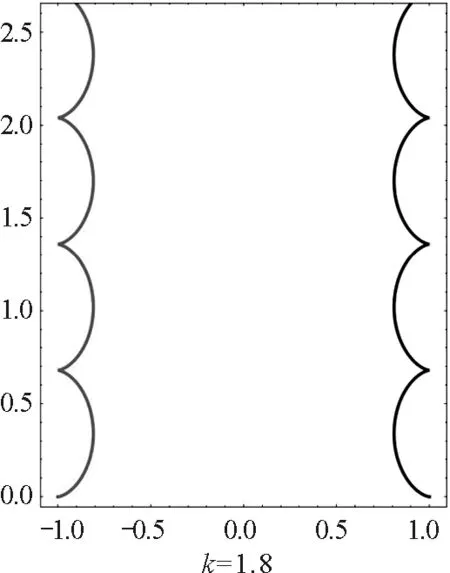
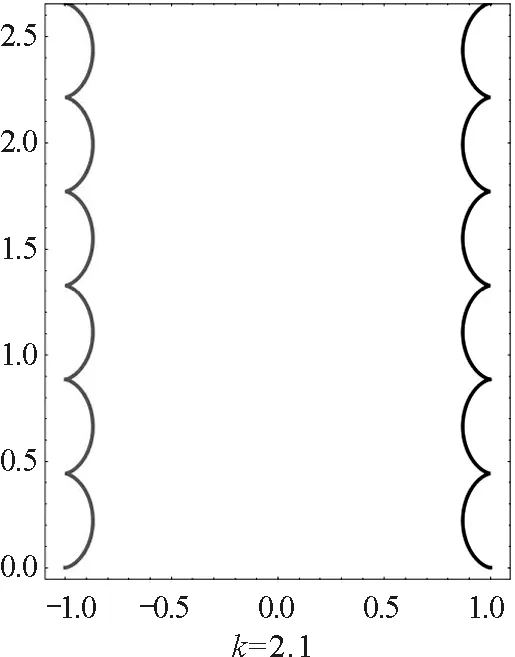
圖4 大于臨界值時不同相對強度磁場下 異號雙電荷周期運動軌跡
3 第三種模型對應的電荷運動軌跡
設起始時候一個正電荷在坐標(1,0)處,另一個正電荷在(-1,0)處.采用極坐標,由對稱性,兩個電荷的坐標分別是(ρ,θ)和(ρ,θ+π).仿照第一種情況的推導,得到量綱歸一化后的運動方程
(12)
(13)
由對稱性,磁場正方向和反方向的軌跡一樣,只是運動方向相反,所以我們只考慮正方向的磁場.數值求解式(12)和式(13),當磁場相對強度k取適當值時,周期轉動角是2π的有理數倍,電荷的運動軌跡會封閉且有對稱性,如圖5所示.
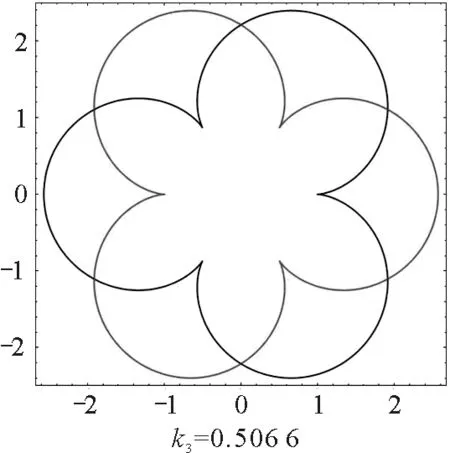
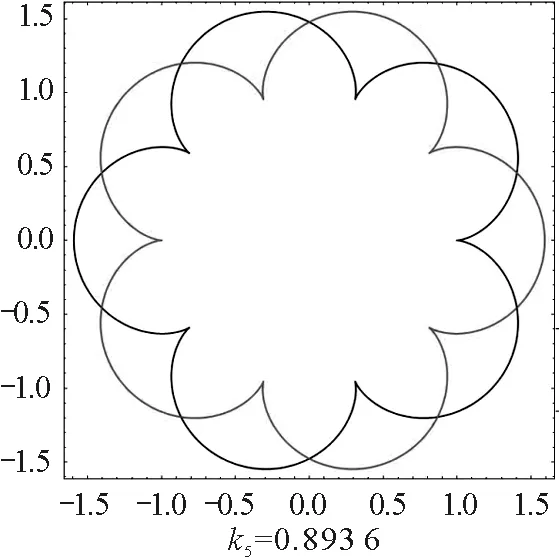
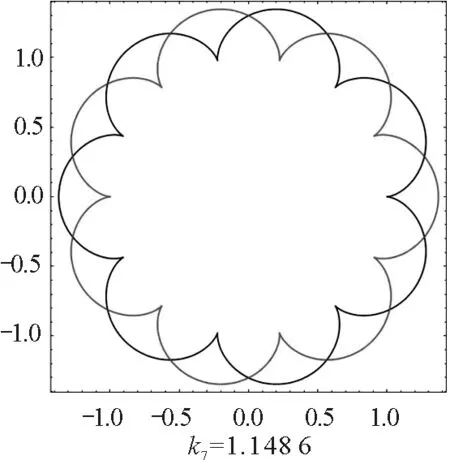
圖5 不同相對強度磁場下同號雙電荷周期運動軌跡
4 結束語
通過數值求解雙電荷在勻強磁場中的運動方程,發現繞固定電荷運動的電荷軌跡具有周期性,磁場相對強度取適當值時,軌跡具有封閉對稱性;自由異號雙電荷存在一個臨界磁場,小于這個臨界值,它們會相遇;大于這個臨界值,它們會做對稱的周期運動.自由同號雙電荷則做對稱的周期運動,當磁場相對強度取適當值時,軌跡具有封閉對稱性.以上3種軌跡,推廣了文獻中電荷運動軌跡,給物理中的運動軌跡曲線寶庫增加了新成員.
1 汪靜誼.電子在相互垂直的電場和磁場中運動軌跡的討論.大學物理,1988,7(9):43~45
2 佘守憲,唐瑩.重力場和正交均勻電磁場中的旋輪線(擺線).物理與工程,2001,11(6):12~18
TheMotionTrajectoryofDoubleChargeintheUniformMagneticFields
YangJie
(SchoolofScience,HuZhouTeachersCollege,HuZhou,ZheJiang313000)
JiangFujin
(TheFirstHighSchoolofHuangpiDistrictinWuhan,Wuhan,Hubei430300)
QiuWeigang
(PhysicsVisualStudio,HuZhouTeachersCollege,HuZhou,ZheJiang313000)
The equations of motion of double-charge in the uniform magnetic field are given. The constants of motion and the characteristics of orbits are discussed. The closed symmetric orbits are drawn from the numerical solution.
double charge;uniform magnetic field;orbit
*高等學校力學課程教學研究項目,編號:JZW-15-LX-15;湖州師范學院教改項目,編號:JGB16022;浙江省高校物理教學研究項目,編號:w201709;國家自然科學基金,編號:11475062
楊潔 (1996- ),女,在讀本科生.
2017-02-02)
①《物理通報》湖州工作室、武漢工作室供稿.

