基于AUV垂直面運動控制的狀態增減多模型切換
周煥銀,李一平,劉開周,封錫盛
(1.東華理工大學 機械與電子工程學院,江西 南昌 330013; 2.中國科學院沈陽自動化研究所 機器人學國家重點實驗室, 遼寧 沈陽 110016)
基于AUV垂直面運動控制的狀態增減多模型切換
周煥銀1,2,李一平2,劉開周2,封錫盛2
(1.東華理工大學 機械與電子工程學院,江西 南昌 330013; 2.中國科學院沈陽自動化研究所 機器人學國家重點實驗室, 遼寧 沈陽 110016)
自主水下機器人(autonomous underwater vehicle, AUV)系統垂直面運動具有強耦合性、非線性等特點導致AUV系統垂直面難以精確控制,且其縱傾角需控制在某一閾值內,以保證系統安全。根據以上控制要求與AUV垂直面運動模型特點,提出將其解耦為深度控制子模型與縱傾角控制子模型,構建AUV系統垂直面運動控制模型集, 根據模型集所含兩子模型特點,提出了狀態變量增減的多模型切換的概念。基于切換系統穩定判據——共同Lyapunov函數法,提出了變加權多模型切換策略,實現了切換過程的穩定性,避免了切換過程的抖動問題。多次湖泊試驗證明,加權多模型切換策略避免了由于期望深度變化而造成的執行機構飽和、深度和縱傾角超調量過大等問題,且改善了AUV系統深度運動的靜動態控制品質。
自主水下機器人; 加權多模型切換控制; 共同Lyapunov函數; 垂直面控制模型; 縱傾角控制模型; 切換系統
自主水下機器人(autonomous underwater vehicle, AUV)系統是一種復雜的非線性耦合系統,且外界環境干擾較難精確描述,這增加了AUV系統運動控制策略設計的難度[1-2]。多模型控制法能夠根據被控對象的控制特點設置多個子模型逼近被控對象的全局動態特性,根據各子模型特點設計相應控制策略,建立控制器集,通過模型間的穩定切換達到快速響應外界控制需求的目的[3]。 多模型切換控制的控制優勢逐漸得到水下機器人運動控制領域的關注。針對復雜環境下AUV系統的運動控制特點,AGUIAR A P等構建了多模型控制技術,解決了多模型間的平滑切換問題,實現了系統全局穩定性[4],解決了欠驅動AUV定深、定向、回轉等運動控制和路徑跟蹤問題[5]。Cavalletti M等針對ROV系統運載模式不同,采用基于神經網絡的切換控制策略法,通過仿真驗證了切換系統的魯棒性[6]。文獻[7]采用基于頻段模型切換的多控制器法,通過仿真驗證了此控制算法在4種不同海況下所具有的良好定位控制性能。 文獻[8]延拓了多模型控制法中的相關理論,提出了在線選取最佳控制策略的控制庫法,采用基于能量函數的直接切換法,實現了控制策略的穩定轉換,并實現了近水面水下機器人系統的航向控制。 文獻[9]通過對船舶航向模型的研究設置了多個航向控制子模型,根據這些模型設置了PID控制庫,采用基于系統縱向速度、外界環境的直接切換法選取控制策略,由于采用的是直接切換法,從系統輸出曲線可以看出系統在切換瞬間運動狀態有較大的抖動。文獻[10]通過船舶試驗證明了采用PID控制、滑模控制兩種控制策略相對一種控制策略具有更強抗干擾能力。基于多模型切換的多控制策略研究不僅簡化了控制策略設計的難度,且針對不同控制模式設置不同控制策略,提高了系統運動控制性能。
傳統多模型切換系統的研究多集中于狀態空間一致的研究[11-12],而對于狀態空間不一致的多模型切換問題的研究較少。WANG P K C等提出了狀態空間縮放法(dilation and contraction)將子系統統一到相同維數下,對非同維線性多模型切換系統的穩定問題進行研究,然而,此方法增加了切換系統的維數,增加了切換策略設計的難度[13]。
為了解決AUV系統垂直面運動狀態間的強耦合性,本文設置了基于狀態變量增減的多模型切換控制法。根據所研究AUV系統運動控制特點推導了相關切換控制理論,以平緩切換過程控制執行機構以及狀態變量的抖動。
1 AUV垂直面運動控制模型集
AUV系統垂直面控制模型是由垂向力方程、縱傾力矩方程以及從運動坐標系到固定坐標系間的轉換方程組成。文獻[14]將水平面的相關狀態量忽略,縱向速度作為系統的模型參數進行處理,獲得AUV系統垂直面的控制模型。
假設1:縱向速度變化平緩;
假設2:為了避免所研究AUV系統在執行任務期間出現危險,通常限制縱傾角變化范圍為弧度,此條件滿足:sinθ≈θ;
假設3: 垂向速度w很小或可忽略不計。
根據以上三條假設構建垂直面控制模型集。
若假設1~3都滿足,垂直面控制模型可設置為
(1)
當任務執行過程中滿足預設條件1、2,垂直面控制模型為
(2)
縱傾角控制模型為
(3)
式中:Mz、Mw與Mθ分別代表深度控制、垂向速度控制與縱傾角控制子模型;z為垂向軸位移,m,θ為縱傾角,rad;u為縱向速度,m/s;w為垂向速度,m/s;q為縱傾角速度,rad/s;δs為驅動AUV系統垂向運動的水平舵舵角,rad。其中h為載體的穩心高,G為載體自身的重量,hG≈zGW-zBB系統入水后所受的靜力矩。其他未描述符號為水動力參數,具體含義請參見文獻[14]。
由于所研究被控對象AUV系統縱傾角約束于(-25°,25°),所以假設2成立,本文所研究AUV系統控制執行機構為水平舵,垂向速度w很小滿足假設3,所研究垂直面模型集由方程(1)與方程(3)組成。
2 非完全同態多模型切換策略
本文所研究AUV系統垂直面控制模型集主要為狀態變量增減的非完全同態多模型切換問題,本文將以此為主,研究多模型切換策略的設計。
說明:1) 本節所涉及的下標含有i,j標號的符號或變量為模型集中所含的第i個或第j個子模型相關的符號或變量; 2) 同態是切換前后各子系統具有完全相同的狀態變量。
2.1 非完全同態多模型切換系統相關定義
本節基于線性與非線性多模型穩定切換的定義,延拓了非完全同態多模型穩定切換的概念。
設非完全同態多模型切換系統描述形式為
(4)
模型切換順序為從子模型Mi切換到Mj記作Mi|→Mj(其中|→表切換的方向),切換后系統狀態空間發生變化,由狀態向量空間xi切換到向量空間xj,即系統從某一運動控制模式切換為另一運動控制模式后系統狀態變量發生變化。
定義1:多模型控制策略根據系統運動狀態所構建的各子模型的階次(維數)不完全相同或狀態變量不完全相同稱為非完全同態多模型切換系統。水下機器人系統垂直面控制模型集:
(5)
其包含運動子模型Mz與子模型Mθ,其狀態變量空間不完全相同。
定義2:當系統由模型Mi切換到模型Mj后,若系統的狀態向量空間xi包含于狀態向量空間xj,即切換后的狀態空間在原狀態空間的基礎上增加,則稱為狀態變量增加的非完全同態多模型切換,如式(5),由Mθ切換為Mz。狀態變量增加的多模型逆向切換即切換后的狀態空間在原狀態空間的基礎上縮減,則稱為狀態變量減少的非完全同態多模型切換,如式(5),由Mz切換為Mθ。
定義3[15]:多模型切換過程中,若其輸出信號連續無抖動現象,則稱切換控制輸出信號平穩。
定義4[15]:若系統所含狀態量在運行中無抖動且在預設范圍內連續平滑運行,則稱切換系統穩定。若切換過程中,各狀態量在預設范圍內逐漸趨近于某一定值,則稱切換系統漸近穩定。
為了研究方便,本文延拓了非完全同態多模型切換控制策略。
設子模型所采用的控制律為
(6)
模型Mj的控制律為
(7)
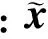
2.2 基于狀態變量減少的多模型切換策略
定義狀態變量減少的多模型切換系統,設切換前子模型MiD為
(8)
其對應控制律為
(9)
式中:下標D表示切換后系統狀態變量減少,A**為子模型系統矩陣所含的各子矩陣。子模型MiD的控制律如式(6)。
切換后子模型MjD為
(10)
(11)
下面根據多模型切換系統的穩定判據共同Lyapunov函數法推導關于狀態變量減少的非完全同態多模型穩定切換策略。
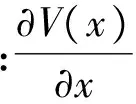
推論1:(狀態變量減少的共同Lyapunov函數穩定判據):
若切換系統MiD|→MjD各子系統在其對應控制律作用下滿足如下兩條件:
則稱多模型系統具有共同Lyapunov函數Vj。
證明:由條件1知:
(12)
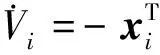
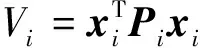
推論2:若切換系統MiD|→MjD滿足如下條件:
2)模型MjD在控制律δj(式(11))作用下穩定。
則基于狀態變量減少的多模型切換系統穩定。
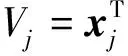
構建子模型MiD的Lyapunov函數Vi:
(13)
(14)
切換系統的Lyapunov函數滿足條件:
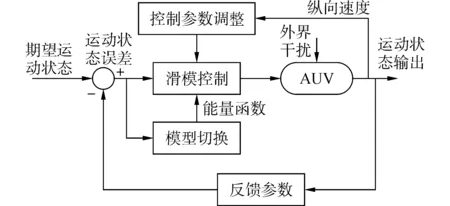
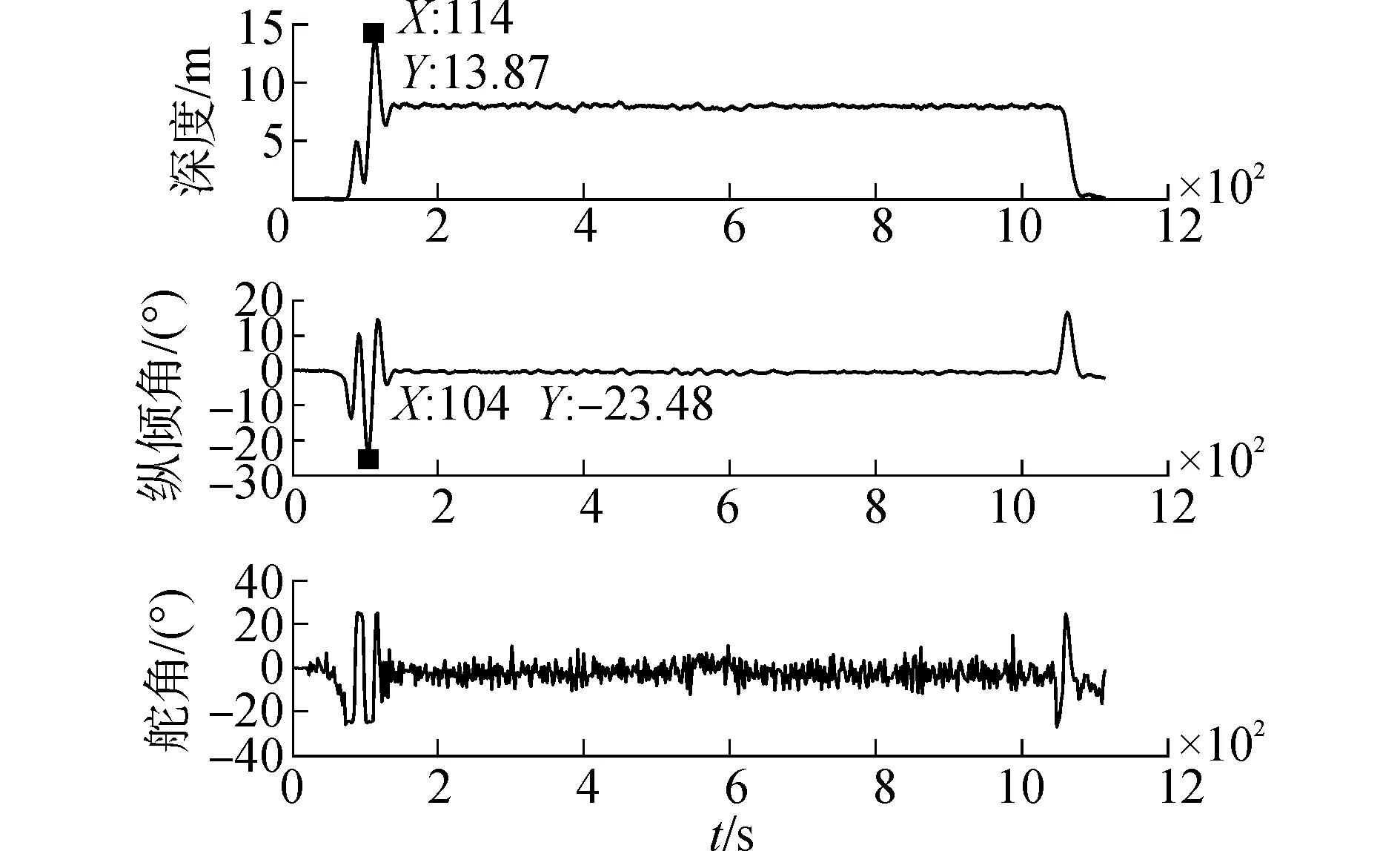
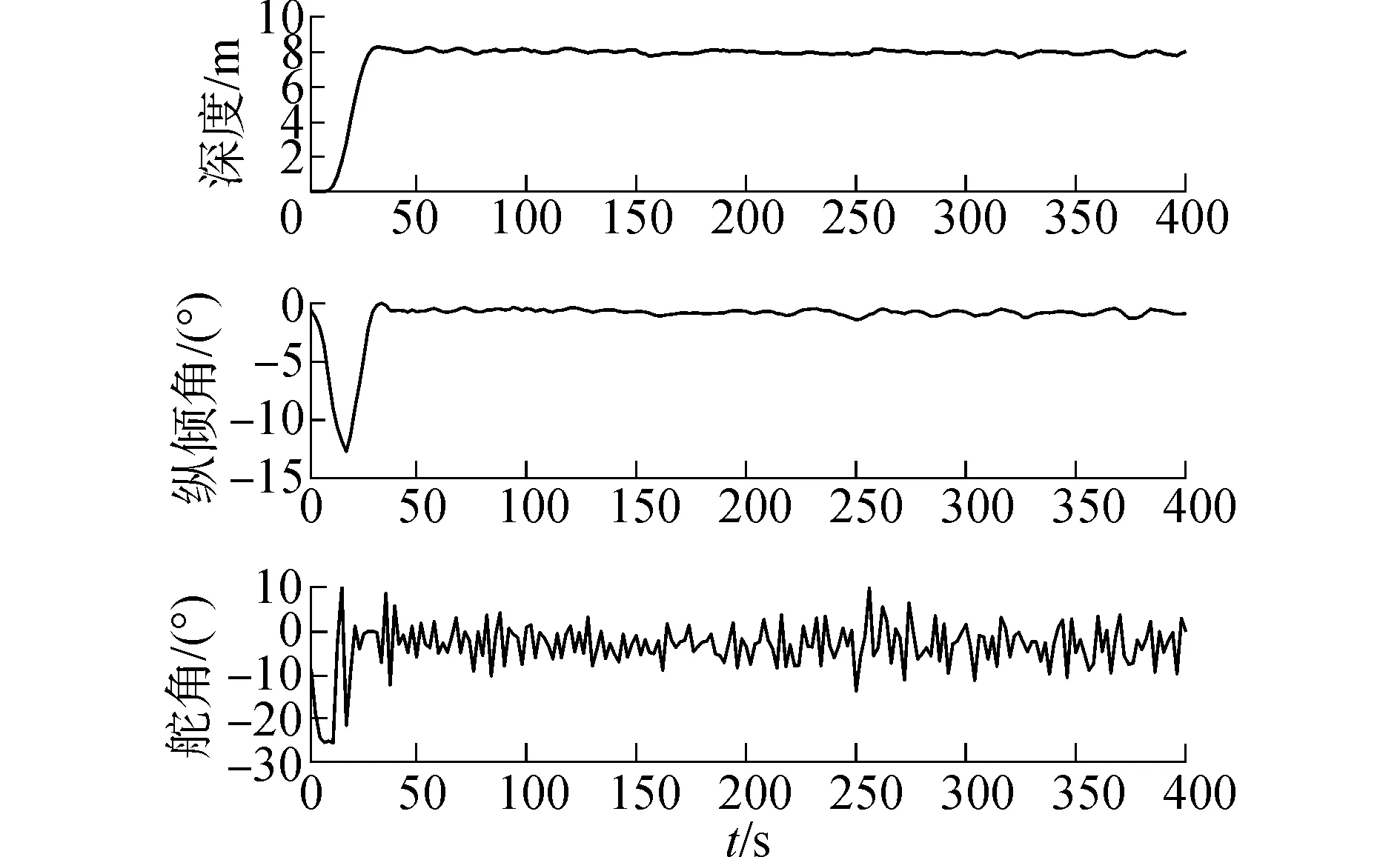
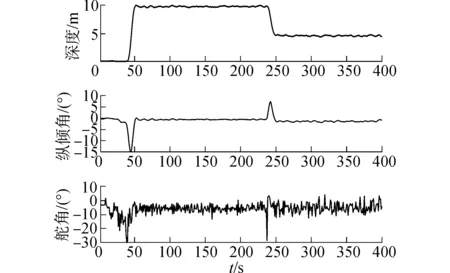
Vj (15) 沿模型MjD對函數(13)求導,有 (16) 推論3:若切換系統MiD|→MjD切換瞬間滿足: 1)子模型MiD(方程(8)),MjD(方程(10))在對應控制律δi,δj作用下穩定,且系統切換前后控制執行機構不變(對于本文所研究AUV系統深度控制而言,控制執行機構是指系統的水平舵舵角); 3)系統能量函數 切換過程所采用加權多模型切換控制律為 (18) 式中:α(t)與β(t)分別為切換前后對應的加權因子。 若切換系統滿足以上條件,則切換瞬間穩定。 證明:切換系統控制律為式(18),切換過程可描述為 (19) 由于系統切換前后控制執行機構不變,故切換前后各子系統控制律所代表的量相同,在根據條件1與加權因子所滿足的條件α(t)+β(t)=1,式(19)可描述為 (20) 切換后系統模型為 (21) (22) 根據推論2可知系統在切換過程中的能量函數漸近衰減,模型切換瞬間穩定。 為了避免直接切換導致系統控制執行機構控制量的瞬間巨變問題,實現切換系統的平穩切換,本文擬設置加權多模型切換控制律(18)。 2.3 狀態變量增加的多模型切換 狀態變量增加的多模型切換系統是指切換后有新的狀態變量增加的切換系統。 設切換前的模型MiI為 (23) 式中:下標I表示切換后系統變量增加,切換后的模型為MjI: (24) (25) 模型MjI在控制律(26)作用下穩定。 (26) 推論4:若切換系統MiD|→MjD所含各子系統在其對應控制律作用下滿足如下兩條件: 則稱基于狀態變量增加的非完全同態多模型切換系統具有共同Lyapunov函數Vj。 證明過程為推論1的逆推導。 3.1 AUV系統垂直面運動模型 圖1 AUV系統深度控制方框圖Fig.1 The block diagram of AUV depth control 3.1.1AUV系統三階深度控制模型及其控制策略 深度控制模型采用方程組(1),將其整理為狀態空間表達式為 (27) S=q-c1θ-c2ez (28) 構建滑模面控制模型: (29) 根據狀態反饋控制法[16]配置模型(29)的期望閉環極點為λz與λθ,獲取狀態反饋控制律: (30) (31) 其中,構建狀態變量誤差ez=z-zd,eθ=θ-θd,eq=q-qd,(zd、θd、qd分別為期望深度、縱傾角、縱傾角速度,均為標量),其中d為期望達到的量。 由于通常期望縱傾角θd=0與期望縱傾角速度qd=0,將eθ=θ,eq=q,故狀態方程(27)的狀態誤差表達式為 (32) (33) 構建含有滑模面S變量的狀態方程,將式(33)代入模型(27),基于滑模面(式(27))的狀態方程可表述為 (34) 設期望滑模面微分方程為 (35) 則由式(33)、(35)得: (36) 即 b1δs=-0.01S (37) 根據式(37)推導三階深度控制模型的控制律δs3: (38) 將相關的水動力參數、系統靜力矩等代入控制律(38),由于系數a1、a2、b1含有狀態變量縱向速度(此狀態變量變化平穩),控制律δs3的控制參數根據縱向速度的變化而動態變化,試驗證明此方案可以有效避免耦合狀態項間的相互干擾。 3.1.2AUV系統二階深度控制模型及其控制律 為了解決當深度偏差過高而造成縱傾角迅速變大或超出閾值問題,采用二階縱傾角控制模型(3)進行縱傾角θ的控制,控制律采用動態反饋法,設期望極點為λθ與λq。根據式(32)可知,其狀態誤差方程描述形式為 (39) 根據狀態反饋控制法[16],獲取二階模型的控制律δs2為 (40) 其中:c3=λθ+λp,c4=λθλp。 3.2 AUV垂直面兩子模型切換控制策略設計 由于AUV系統兩控制子模型在各控制律作用下具有漸近穩定性,根據推論1與推論4可知模型(32)與模型(39)構建的控制模型集,滿足狀態變量增加或減少的共同Lyapunov函數穩定判據條件,故兩子模型控制律可實現兩模型間的任意切換。 本文所采用的基于狀態變量空間縮減的非完全同態多模型切換控制策略如下: 2) 當能量函數V≤4時,切換到三階深度控制律δs=δs3,實現AUV系統的深度控制。 4)從控制律(40)切換到控制律(38)瞬間,根據推論4的相關條件設置相似于第3)條所描述的加權因子α(t)、β(t),其中切換控制律為δ=β(t)δs3+α(t)δs2,α(t)+β(t)=1。 3.3 湖泊試驗數據分析 本文通過AUV系統深度控制的湖泊試驗數據,分析基于狀態變量增減的多模型切換法的控制優勢。湖試安排:1)檢驗三階滑模控制試驗效果,分析在三階模型控制策略下系統運動控制品質;2)驗證狀態變量增加的多模型切換效果;3)通過增加下潛深度與變深試驗驗證多模型切換控制的控制品質;4)通過變化AUV系統下潛深度,驗證切換策略。 基于三階深度模型的定深控制結果分析,此次湖試AUV系統下潛深度為8 m。從湖試數據曲線(如圖2)分析AUV系統垂直面相關狀態量與控制量的輸出,其中深度控制出現了較大的超調量δp=73%,分析其原因是由于AUV系統縱傾角過大所引起、多次達到閾值±0.44rad即±25°、且震蕩等控制品質問題;系統控制執行機構水平舵長時間(50s)處于滿舵狀態,這些都是不期望的現象。 圖2 三階深度控制策略δs3控制下輸出曲線Fig.2 Curves under the three-dimension depth controller δs3 基于狀態變量增減的非完全同態多模型切換在AUV系統定深控制試驗中的驗證,仍采用定深8m的試驗,試驗結果 (如圖3)表明:AUV系統深度控制品質得到改善,深度控制超調消失;縱傾角控制品質得到改善無震蕩現象;通過多模型切換策略的設置使得水平舵滿舵時間大大縮短。 圖3 基于狀態變量增加的多模型切換垂直面輸出曲線Fig.3 Curves under the multi-model switching control with increasing dimensions 為了驗證基于狀態變量增減的多模型切換控制律能否保證切換過程的平穩性,本文采用AUV系統的變深控制試驗,任務為AUV先定深10m,450s后定深5m,湖試結果如圖4所示。AUV系統深度控制試驗表明,AUV系統深度與縱傾角的控制具有調節時間短、無超調、無靜態誤差等良好動靜態品質。在變深為5m的控制過程中狀態變量減少的切換有效地控制了水平舵舵角的變化。 圖4 基于狀態量增減的多模型切換變深控制輸出曲線Fig.4 Curves under the multi-model switching control with decreasing dimensions 1)所提出的狀態變量增減的非完全同態多模型切換法將復雜的垂直面運動控制問題分解為深度控制與縱傾角控制兩類方式。 2)多次AUV湖試驗證了基于狀態變量增減的多模型切換控制策略,可消除AUV系統深度控制的超調量,避免了縱傾角過大現象。 3)加權多模型切換控制策略可以避免由于深度突然變化而造成控制執行機構的抖動,提高了AUV系統的深度控制的動、靜態品質。 [1] 封錫盛,李一平,徐紅麗. 下一代海洋機器人-寫在人類創造下潛深度世界紀錄10912米50周年之際[J]. 機器人, 2011, 33(1): 113-118. FENG Xisheng, LI Yiping, XU Hongli. The next generation unmanned marine vehicles dedicated to the 50 anniversary of the human world record diving 10912 m[J]. Robot, 2011, 33(1): 113-118. [2] 徐玉如,李彭超. 水下機器人發展趨勢[J]. 自然雜志, 2011, 33(3): 125-133. XU Yuru, LI Pengchao. Developing tendency of unmanned underwater vehicles[J]. Chinese journal of nature, 2011, 33(3): 125-133. [3] 周煥銀,劉開周,封錫盛. 基于權值范圍設置的多模型穩定切換控制研究[J]. 控制與決策, 2012, 27(3): 349-354. ZHOU Huanyin, LIU Kaizhou, FENG Xisheng. Stability switching of multiple models based on weighting setting[J]. Control and decision, 2012, 27(3): 349-354. [4] AGUIAR A P, PASCOAL A M. Regulation of a nonholonomic autonomous underwater vehicle with parametric mod- eling uncertainty using Lyapunov functions[C]//Proceedings of the IEEE Conference on Decision and Control. Orlando, 2001: 4178-4183. [5] AGUIAR A P, PASCOAL A M. Global stabilization of an underactuated autonomous underwater vehicle via logic-based switching[C]//Proceedings of the IEEE Conference on Decision and Control. Las Vegas, 2002: 3267-3272. [6] CAVALLETTI M, IPPOLITI G, LONGHI S. Lyapunov-based switching control using neural networks for a remotely operated vehicle[J]. International journal of control, 2007, 80(7): 1077-1091. [7] 林孝工,謝業海,趙大威,等.基于海況分級的船舶動力定位切換控制[J].中國造船,2012, 53(3): 165-174. LIN Xiaogong, XIE Yehai, ZHAO Dawei, et al. Switching control for dynamic positioning vessels based on sea states classificaiton[J]. Shipbuilding of China, 2012, 53(3): 165-174. [8] 周煥銀, 封錫盛, 胡志強, 等. 基于多辨識模型優化切換的USV 系統航向動態反饋控制[J]. 機器人, 2013, 35(5): 552-558. ZHOU Huanyin, FENG Xisheng, HU Zhiqiang, et al. Dynamic feedback controller based on optimized switching of multipleidentification models for course control of unmanned underwater vehicle[J]. Robot, 2013, 35(5): 552-558. [9] HAMMOUD S, MOHAMED D. Ship motion control using multi-controller structure[J]. Ocean engineering, 2012, 55: 184-190. [10] NGUYEN T D, SORENSEN A J, QUEK S T. Design of hybrid controller for dynamic positioning from calm to extreme sea conditions[J]. Automatica, 2007, 43(5): 768-785. [11] XIA Chiyun. Optimal control of switched systems with dimension-varying state spaces[D]. Los Angeles: University of California, 2007. [12] BALDI S, BATTISTELLI G, MARI D,et al. Multi-model unfalsified switching control of uncertain multivariable systems[J]. International journal of adaptive control and signal processing., 2012, 26(8) SI: 705-722. [13] WANG P K C, HADAEGH F Y. Stability analysis of switched dynamical systems with state-space dilation and contraction[J]. Journal of guidance, control, and dynamics, 2008, 31(2): 395-401. [14] 蔣新松, 封錫盛, 王棣棠. 水下機器人[M]. 沈陽:遼寧科學技術出版社, 2000: 150-183. JIANG Xinsong, FENG Xisheng, WANG Ditang. Underwater vehicles[M]. Shenyang:Liaoning Publisher Science and Technology, 2000: 150-183. [15] LIBERZON D. Switching in systems and control [M]. Boston: Birkhauser, 2003. [16] 劉豹. 現代控制理論[M].3版.北京:機械工業出版社, 2006: 188-200. 本文引用格式: 周煥銀,李一平,劉開周,等. 基于AUV垂直面運動控制的狀態增減多模型切換[J]. 哈爾濱工程大學學報, 2017, 38(8): 1309 -1315. ZHOU Huanyin, LI Yiping, LIU Kaizhou, et al. Multi-model switching control laws for the vertical plane control of an autonomous underwater vehicle[J]. Journal of Harbin Engineering University, 2017, 38(8): 1309-1315. Multi-model switching control laws for the vertical plane control of an autonomous underwater vehicle ZHOU Huanyin1, LI Yiping2, LIU Kaizhou2, FENG Xisheng2 (1.School of Mechanical and Electronic Engineering, East China University of Technology, Nanchang 330013, China; 2.State Key Laboratory of Robotics, Shenyang Institute of Automation Chinese Academy of Sciences, Shenyang 110016, China) System vertical plane motion states have strong coupling and nonlinear characteristics, thereby making precise vertical plane control of an autonomous underwater vehicle (AUV) system difficult. Moreover, the pitch angle, which is one of the state variables of vertical plane control, should not exceed a threshold; otherwise, the AUV system might encounter damage issues, such as deep/over control and even more serious situations. In accordance with the motion characteristics of an AUV system with different control requirements on a vertical plane, the vertical plane motion model was decoupled into two mathematical sub-models (depth control model and pitch angle control model) to build the vertical plane dynamic model set of an AUV system. A corresponding control strategy was adopted according to the sub-model characteristics of the model set. Given that the system state variables and the number of dimensions will change before and after switching of sub-models, the concept of multi-model switching is based on an increase and decrease of state variables. To avoid chattering due to switching between the two sub-models, the variable weighting multi-model switching strategy was proposed on the basis of common Lyapunov function, which is the stability theory for switched systems, thereby ensuring stability during the switching process. Lake trials for the vertical plane of a type of AUV prove that the weighted multi-model switching strategy avoids saturating the executor as a result of a change in expected depth and overshooting of depth and pitch angle, among others. The weighted multi-model switching strategy improves the static and dynamic control quality of the deep movement of AUV systems. autonomous underwater vehicle; multi model switching control law with weighting values; common Lyapunov; vertical plane model; pitch control model; switching control system 2016-07-08. 日期:2017-06-02. 國家自然科學基金項目(51409047);機器人學國家重點實驗室開放基金項目(2016-O05). 周煥銀(1975-), 女, 副教授; 封錫盛(1941-), 男, 研究員,博士生導師,中國工程院院士. 周煥銀,E-mail:hyzou@ecit.cn. 10.3969/j.issn.1006-7043.201607021 TP273 A 1006-7043(2017)08-1309-07 網絡出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20170602.2003.008.html
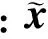
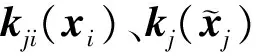
3 AUV湖試驗證分析
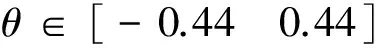
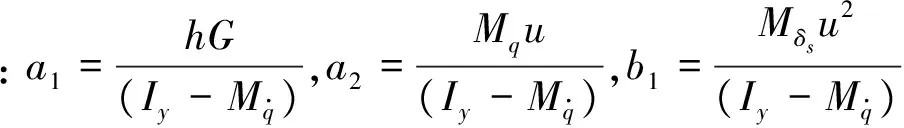
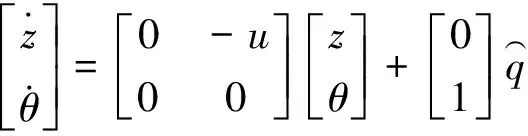
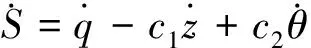
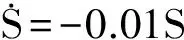
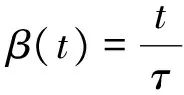
4 結論

