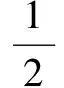函數單調性的應用
杜紅全
(甘肅省康縣教育局教研室,甘肅 隴南 746500)
函數單調性的應用
杜紅全
(甘肅省康縣教育局教研室,甘肅 隴南 746500)
單調性是函數之“魂”,是函數的重要性質之一,文章舉例說明它在比較大小、解不等式、解方程、求參數的值或取值范圍、求函數的最值或值域、求值、證明不等式等方面得一些應用,希望起到拋磚引玉之功效.
函數;單調性;應用
函數單調性是函數的重要性質之一,也是平常考試和高考中數學的重點和熱點內容之一.它在高中數學的各個分支中都有著極為重要的應用,在解題過程中如果應用得好,常能起到事半功倍的效果,下面舉例說明.
一、比較大小
例1設函數f(x)是(-∞,+∞)上的減函數,則( ).
A.f(a) C.f(a2+a) 分析 由減函數的定義可知,只需比較各組函數值的自變量的大小. 點評 本題還可以用排除法解之.利用單調性比較大小時,必須將其轉化為同一單調區間內的兩個函數值,否則不能比較其大小. 例2 已知f(x)在它的定義域[-17,+∞)上是增函數,且f(3)=0,解不等式f(x2-7x-5)<0. 分析 解本題只需要利用函數的單調性去掉函數關系符號“f”, 使抽象的不等式問題轉化為具體的不等式問題. 點評 利用單調性解不等式就是利用函數在某個區間內的單調性,推出兩個變量的大小,然后去解不等式;去掉函數關系符號″f″的主要依據是函數的單調性,同時要特別注意函數的定義域,否則可能產生增解. 例3 解方程(x2-x+1)5-x5+4x2-8x+4=0. 解析 由原方程變形為(x2-x+1)5+4(x2-x+1)=x5+4x.由于函數f(t)=t5+4t在R上單調遞增,又f(x2-x+1)=f(x),所以x2-x+1=x,解得x=1.故原方程有唯一實數解x=1. 點評 解本題的關鍵是對原方程進行變形,與函數f(t)=t5+4t產生聯系,再根據函數的單調性列出方程即可. 例4 若函數f(x)=|2x+a|的單調遞增區間是[3,+∞),則a=____. 點評 本題考查的是函數的單調性.做本題的關鍵是將原函數化為分段函數,然后根據單調遞增區間列出關于a的方程即可.本題還可通過畫出函數圖象來求解. 例5 已知函數f(x)=x2+2(1-a)x+2在(-∞,4]上是減函數,求實數a的取值范圍. 分析 二次函數是我們最熟悉的函數,只要遇到二次函數畫圖象,也可以不將圖象畫出,而在大腦中出現,這樣就給我們研究問題帶來了很大的方便.對于不熟悉的函數,可以利用單調函數的定義去研究與單調性有關的問題. 點評 二次函數問題要注意三點:一是開口方向;二是對稱軸;三是頂點坐標. 分析 當所給的函數圖象不易作出時,可考慮利用函數的單調性求函數的最值,即先判斷函數的單調性,再求最值. 點評 函數f(x)在區間[a,b](a 例7 設實數a,b滿足條件a3-3a2+5a=1,b3-3b2+5b=5,求a+b的值. 分析 待求代數式的值,可視為相應函數的一個特殊值,再利用該函數的單調性,把函數值的相等轉化為自變量的相等,從而巧妙獲解. 解 由已知條件式的特征,構造函數f(x)=x3-3x2+5x,則有f(a)=1,f(b)=5.而f(x)=(x-1)3+2(x-1)+3.令u=x-1,則g(u)=u3+2u是單調增函數,還是奇函數,則有f(a)=g(a-1)+3=1,f(b)=g(b-1)+3=5,即g(a-1)=-2,g(b-1)=2,則g(a-1)=-g(b-1)=g(1-b).由g(u)=u3+2u是單調增函數可得a-1=1-b,因此有a+b=2. 點評 求解本題的關鍵是構造函數f(x)=x3-3x2+5x,利用函數的單調性和奇函數的性質,列出關于a,b的方程,把a+b整體解出,屬于整體求值. 分析 通過構造函數轉化為比較單調函數的兩個函數值問題. 點評 把證明的不等式問題轉化為函數問題,關鍵在于轉化為什么樣的函數,這就要求從被證的不等式的形狀、特點去入手,產生聯想去尋找相應的基本函數,然后利用函數的單調性加以證明. 當然,利用函數的單調性還可以判斷復合函數的單調性以及畫函數的圖象,在這里就不舉例說明了. 鏈接高考 1(2015江蘇,文理7)不等式2x2-x<4的解集為 .(答案:{x|-1 2(2016全國Ι卷,理8)若a>b>1,0 A.ac C.alogbc [1]杜紅全.別忘了讓平面向量與三角形談“心”[J].中學生數學,2014(3). [2]杜紅全.求三角函數值域的常用方法[J].中學生數學,2014(5). [責任編輯:楊惠民] 2017-05-01 杜紅全(1969.9-), 男,甘肅康縣人,中學高級教師,西北師范大學本科畢業,從事中學數學教育. G632 B 1008-0333(2017)19-0002-02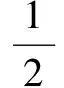
二、解不等式

三、解方程
四、求參數的值或取值范圍

五、求函數的最值或值域


六、求值
七、證明不等式