高中數學核心素養之數學抽象能力的培養實踐初探
周先華
(四川省成都市玉林中學,四川 成都 610000)
高中數學核心素養之數學抽象能力的培養實踐初探
周先華
(四川省成都市玉林中學,四川 成都 610000)
數學抽象是高中數學核心素養的6大組成部分之一.在課堂教學中,要讓學生實質性地參與數學抽象的每一個過程,認識數學抽象這種創造性活動的一般性原則與方法.在均值不等式教學中,通過對其幾何意義與證明、三個相鄰平均值之差的大小比較的探究,發現不等式與平面幾何、三角、函數、導數之間的聯系,進行了一堂成功的數學抽象核心素養培養的嘗試,轉變數學知識學習觀,尊重學生的個體知識,嘗試進行深度學習與協作學習.
數學抽象;高中數學核心素養;均值不等式;深度學習
我國數學教學已經從20世紀50年代的“數學知識的教學”發展到今天的“數學素養的教學”階段,即數學教學不僅要傳授知識和培養能力,而且更要掌握核心素養,發展情感與態度,立德樹人.而普通高中數學課程標準(修訂稿)的一個重要特點就是“把學生發展為本,落實立德樹人根本任務,培養和提高學習的數學核心素養”作為高中數學課程的宗旨,并明確了高中數學核心素養的6個方面:數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析.而數學抽象作為六大核心素養之首,它既是數學的基本思想,也是形成理性思維的重要基礎,它反映了數學的本質特征并貫穿于數學的產生、發展與應用的整個過程中.因此,數學抽象能力在2016年全國高考考試大綱(數學)中也被明確列為高考七大“能力要求”之一.
但是,怎樣在高中數學教學過程中進行數學抽象能力的培養呢?
一、數學核心素養下的數學抽象能力
數學抽象是通過觀察、分析,撇開數學對象的外部的、偶然的東西,抽象出其本質、內在、必然的東西,從空間形式和數量關系上揭示數學對象的本質和規律的一種數學研究方法.它通過對具體而生動的數學問題進行分析與提煉,發現其本質,進而再概括出一些結論,并將其應用于解決新的問題之中,這就是數學抽象概括能力.
在數學核心素養下的數學抽象能力,主要表現在四個方面:1.形成數學概念和規則;2.形成數學命題與模型;3.形成數學方法與思想;4.形成數學結構與體系.
數學抽象是一種創造性的活動.這種創造性活動有其常用的、一般性的原則與方法:概念意義上的一定層次上的普遍性和概括性、表達形式上無歧義的邏輯精確性和簡潔性、弱抽象與強抽象方法、類比聯想、對偶化、悖向思維和美學方法等等.下面通過均值不等式的教學,對高中數學核心素養之數學抽象能力的培養進行實踐探究.
二、均值不等式≤≤≤(a>0,b>0)的探究
(一)問題提出


結合歷年高考和全國高中數學聯賽試題,提出了下列探究問題:

5.你還能提出相關的探究問題嗎?請提出問題并嘗試解決.
(二)問題探究

由上圖1可以得到a2+b2≥2ab.由此聯想到可以由完全平方公式證明此結論:

點評 這一步看似簡單,但它是均值不等式證明的基石.它在教材給出的方法基礎上進行類比聯想思維,是一種同向思維方法,同時也是數學抽象方法的常用方法.

有了前面的探究過程,可以順利地得到這個擴展的均值不等式的代數證明方法:

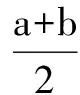
(3)顯然,三個不等式都是當且僅當a=b時取等號.


上述探究過程讓學生很有成就感,極大地提升了學習興趣.但怎樣得到此式中另兩個代數式的平面幾何解釋,卻需要更深入的探究.
我們把這個問題分成兩個小步驟:






(2)在平面幾何表示中證明均值不等式

三、比較兩個相鄰平均數的差的大小



(2)利用函數思想比較P,Q,R的大小

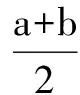

①證明Q≥P



②證明P≥R


由表2、表3可知,藥后30 d,各藥劑處理小區內雜草株防效相對于藥后15 d整體略有降低,可能是由試驗小區內新增雜草較多所導致。1%甲基二磺隆·雙氟磺草胺可分散油懸浮劑各劑量處理對雀麥、播娘蒿、薺菜的株防效、鮮質量防效均在80%以上,總體防除效果較好;單劑30 g/L甲基二磺隆可分散油懸浮劑對雀麥的株防效、鮮質量防效仍高于90%,對播娘蒿、薺菜的防效略差;單劑50 g/L雙氟磺草胺懸浮劑對播娘蒿、薺菜的株防效、鮮質量防效仍高于90%,但由于對雀麥無效,總體防效較差。
結合(1)(2)知,Q≥P≥R.
點評 本探究從不等式到平面幾何、再到平面三角、解析幾何、函數與導數,尋求在各大知識板塊的交匯點處研究問題的內在聯系,提出并解決問題.
在比較P,Q,R的大小時,以角度為自變量,構造出函數,再利用研究函數最值的一般性方法——導數法求得函數的最值,從而比較大小.不等式判斷(或證明)本質上就是函數的最值問題.
四、探究收獲與反思
1.轉變數學知識學習觀,讓知識學習過程成為數學抽象核心素養形成過程
素養不是知識,知識的積累是素養形成的必要而不充分條件.知識不是被儲存的一堆事實,而是觀念與思維方式;倘若秉持僵化、凝固的知識觀,并以灌輸、訓練的方式教授知識,知識的積累反而會導致素養的衰減甚至冺滅.本探究就是讓均值不等式的結形成與證明、平均數的差的大小比較的過程作為教學的核心,同時從不同知識點之間尋求交匯,從而形成數學抽象能力,進而培養成為學生的數學核心素養.
2.尊重學生的個體知識
尊重學生的個體知識,在教學中表現為預留足夠的時間,把數學概念的形成、方法的產生、思想的提煉等等機會全部留給學生,讓學生感悟出來.并遵循循序漸進的原則,分層推進,發現并肯定學生的閃光點,把成功的機會給予學生.這會極大地鼓勵學生繼續學習數學的勇氣與信心,從而形成數學學習能力,進而培養成為終身學習的能力.
3.轉變數學知識學習的方法,進行深度學習與協作學習
數學知識+數學實踐=數學素養.一切知識,只有成為學生探究與實踐的時候,其學習過程才有可能成為素養發展過程.因此,轉變數學知識的學習方式是素養發展的前提.讓數學知識學習過程實現批判性思維與社會協作的連接.為此,一方面是進行深度學習,讓數學知識學習成為批判性思維和數學問題解決的過程; 另一方面是要進行協作學習,讓知識學習成為交往與協作,即集體創造知識的過程.
[1]羅增儒.從數學知識的傳授到數學素養的生成[J],中學數學教學參考,2016(07):2.
[2]周先華.高中數學解題方法[M].成都:電子科技大學出版社,2015:209
[3]林崇德.對未來基礎教育的幾點思考[J].課程 教材 教法,36(03):3.
[4]張華.論核心素養的內涵[J].全球教育展望,2016(4):10.
[責任編輯:楊惠民]
2017-06-01
周先華(1972.7-),男,四川廣安人,中學高級,大學本科,從事中學數學教學.
G632
B
1008-0333(2017)19-0039-03

