甲醇汽車來了

蘇更林

近日，工信部等八部門聯(lián)合發(fā)布了《關(guān)于在部分地區(qū)開展甲醇汽車應(yīng)用的指導(dǎo)意見》，標志著我國甲醇汽車將逐步走進人們的生活。甲醇，這種無色透明易揮發(fā)的液體化學物質(zhì)，既是一種基本的化工原料，又是一種很有吸引力的替代清潔燃料。甲醇汽車就是甲醇應(yīng)用于車用燃料的一個方向。

甲醇來自哪里

甲醇原本就存在于自然環(huán)境中，是通過多種細菌的厭氧代謝自然產(chǎn)生的。人類何時發(fā)現(xiàn)和利用甲醇已無法考證，但最初分離出純凈甲醇的是英國人羅伯特·波義耳。波義耳是近代化學的開創(chuàng)者。他于1661年從干餾黃楊木中分離獲得了甲醇，因此，甲醇又被稱為“木醇”或“木精”。這也是工業(yè)上制取甲醇的最古老的方法。

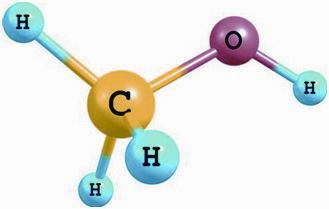
1834年，法國化學家杜馬和皮里哥分析了甲醇的元素構(gòu)成，并確定其化學組成為CH3OH。1905年，法國化學家薩巴蒂爾首先提出由合成氣，即一氧化碳和氫氣的混合物合成甲醇的觀點。1913年，艾尼林和法布里克提出了從煤炭合成氣中合成甲醇，開啟了煤制甲醇的歷史。1923年，德國建成世界上第一座年產(chǎn)3000噸的高壓合成甲醇裝置。目前，世界上的甲醇生產(chǎn)大多采用低壓工藝。

生產(chǎn)甲醇的合成氣來源十分廣泛，包括煤炭、天然氣、焦爐氣、煤層氣等。根據(jù)我國“富煤缺油少氣”的國情，采用煤基甲醇的原料技術(shù)路線，利用低質(zhì)煤、煤層氣、焦爐煤氣等制備甲醇，可以充分發(fā)揮我國煤炭資源的優(yōu)勢。

何為甲醇汽車

甲醇汽車并不是指只能燒甲醇的汽車，而是以甲醇作為主要燃料，也可以燒汽油或者甲醇與汽油混合燃料的汽車。甲醇在汽車上的應(yīng)用主要有摻燒和純甲醇替代兩種方式。

所謂摻燒，是指把甲醇添加在汽油里并用甲醇燃料助溶劑復(fù)配的甲醇汽油混合燃料，通常用甲醇的英文名稱（Methanol）的第一個字母M和甲醇的含量（一般為體積分數(shù)）來表示。如M15、M30、M85、M100分別代表甲醇汽油混合燃料中甲醇的摻入量為15%、30%、85%和100%（純甲醇燃料）。

使用低比例甲醇的甲醇汽油混合燃料，無須對發(fā)動機和裝置進行改造就能直接使用。使用高比例的甲醇汽油混合燃料，由于受到甲醇燃燒特性的限制，需要對發(fā)動機進行改造才能使用。

甲醇混合燃料具有良好的熱效率、動力性、啟動性和經(jīng)濟性，并具有節(jié)能環(huán)保等優(yōu)勢。因此，甲醇汽車的推廣應(yīng)用，將有利于保護藍天白云，對保障國家能源安全也具有重要的意義。

甲醇底氣何在

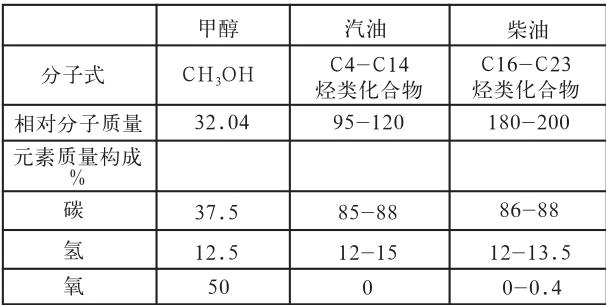
甲醇作為一種高性能、高效率的車用替代燃料，具有低碳、氧含量高、辛烷值高等特性，有利于燃料的充分燃燒，有效提升發(fā)動機的功率，并且具有排放量低的優(yōu)勢。

低碳高氧：甲醇的分子結(jié)構(gòu)為CH3OH，僅含有一個碳原子，因此甲醇燃料可以比汽油少排放15%～20%的碳。甲醇分子中的含氧量高達50%，在氣缸內(nèi)完全燃燒時所需的空氣量遠少于汽油，因此燃燒得更為充分。這樣不僅可以提高發(fā)動機的熱效率，而且還能減少汽車運行時的尾氣（如一氧化碳和碳氫化合物）排放。同時，由于甲醇在燃燒時所需的空氣量少，因此氮氧化物（NOx）生成量會比汽油和柴油少得多。甲醇的燃燒速度很快，一般不會產(chǎn)生顆粒物。

高辛烷值：辛烷值是表征燃料抗爆性的重要指標，其值高表示抗爆性好。抗爆性是指燃料在一定壓縮比發(fā)動機中不產(chǎn)生爆震燃燒的性能。所謂爆震燃燒，是指燃燒性能差的燃料在氣缸內(nèi)發(fā)生爆炸燃燒的一種不正常工作狀態(tài)。通常會使氣缸溫度劇升，燃料燃燒不完全，機器發(fā)生強烈震動，使得輸出功率下降，機件受損。

辛烷值是指在標準實驗條件下，把試油與已知辛烷值的參比燃料（標準燃料）在爆震實驗室實機上進行比較。如果爆震強度相當，那么就說明參比燃料的辛烷值即為試油的辛烷值。參比燃料由異辛烷（辛烷值定為100）和正庚烷（辛烷值定為0）混配而成，兩者按不同體積比進行混配就可以得到辛烷值從0到100的各種參比燃料了。

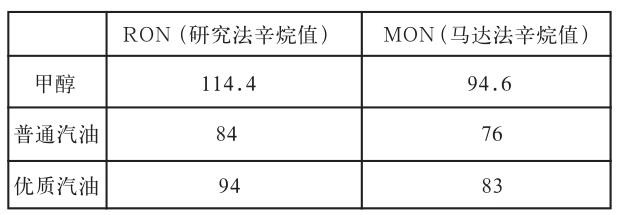
辛烷值分為馬達法（MON）和研究法（RON）兩種，馬達法辛烷值反映燃料在重負荷、高轉(zhuǎn)速時的抗爆性，研究法辛烷值表示燃料在低轉(zhuǎn)速時的抗爆性。辛烷值還有一個意義，就是車用汽油的牌號是按辛烷值來劃分的，如90號汽油就說明該汽油的辛烷值不低于90。

目前，提高汽油辛烷值的主要措施是采用先進的煉制工藝以及使用高辛烷值的調(diào)和劑，如加入甲基叔丁基醚、乙基叔丁基醚或醇類燃料等。甲醇的辛烷值為114.4，遠高于汽油和柴油，抗爆性很好。使用甲醇后可以提高發(fā)動機的壓縮比，進而提高熱效率。

防火安全性：甲醇的自燃溫度為500℃，高于汽油（350℃～468℃）和柴油（270℃～350℃），因此甲醇燃料比汽油和柴油更安全。甲醇燃料在空氣中的著火極限為6.0%～36.5%（體積分數(shù)），也高于汽油（1.4%～6.7%）和柴油（1.5%～8.2%），說明甲醇蒸汽在空氣中的濃度需達到4倍于汽油時才能著火。

碳化工的基石

甲醇一向被譽為是碳化工的基石，是碳一化工的骨干分子。所謂碳一化工，是指以含有一個碳原子的物質(zhì)（如一氧化碳、二氧化碳、甲醇、甲烷等）為原料合成化工產(chǎn)品或液體燃料的有機化工工藝。

在基本有機化工產(chǎn)品中，甲醇的地位僅次于乙烯、丙烯和苯，其下游產(chǎn)品廣泛應(yīng)用于工農(nóng)業(yè)生產(chǎn)、交通運輸以及國防工業(yè)。

在甲醇下游產(chǎn)品樹中，甲醛是一個主干產(chǎn)品，可由甲醇氧化法制得。甲醛作為一種大眾化化工產(chǎn)品，可用作酚醛樹脂、脲醛樹脂、維綸、染料、農(nóng)藥和消毒劑等的原料。

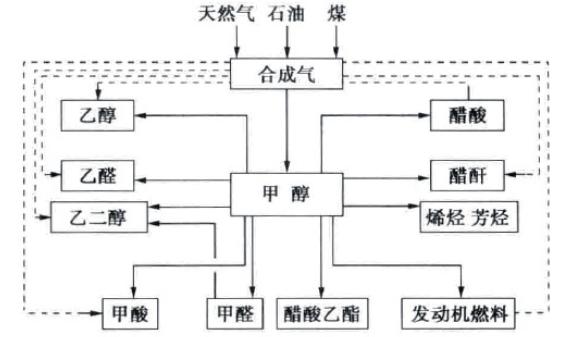
用甲醇和異丁烯作原料催化合成的甲基叔丁基醚，為一種高辛烷值的汽油添加劑，不僅能提高汽油的辛烷值，而且還能改善汽車的性能，降低污染物排放。

采用甲醇脫水法生產(chǎn)的二甲醚，主要用作有機合成的原料，也可用作溶劑、氣霧劑、制冷劑和麻醉劑等，并在制藥、燃料、農(nóng)藥等化學工業(yè)中有許多獨特的用途。