基于NARMA?L2控制器的電力系統穩定性分析

薛蕊+曾實現+馮飛

摘 要： 基于人工神經網絡提出一種新的非線性自回歸移動平均控制器（NARMA?L2），將其用于電力系統的穩定性分析。該控制器應用于同步發電機勵磁系統中能產生相應的輔助控制信號，可以改善阻尼低頻振蕩和電力系統的動態性能。將NARMA?L2控制器用于對單機無窮大電力系統（SMIB）的分析，與傳統電力系統穩定器（CPSS）中的遺傳算法分析相比較， 得到了更好的控制效果。

關鍵詞： 遺傳算法； NARMA?L2控制器； 非線性分析； 電力系統穩定器

中圖分類號： TN915.853?34； TP183 文獻標識碼： A 文章編號： 1004?373X（2017）17?0141?03

Power system stability analysis based on NARMA?L2 controller

XUE Rui， ZENG Shixian， FENG Fei

（Qingdao Huanghai University， Qingdao 266427， China）

Abstract： A new nonlinear auto regressive moving average?L2 （NARMA?L2） controller based on artificial neural network is proposed， and applied to the stability analysis of power system. The controller used in the excitation system of synchronous generator can generate the appropriate assist control signal to improve the dynamic performance of the power system and dam?ping low?frequency oscillation. The NARMA?L2 controller is adopted to analyze the single machine infinite bus （SMIB） system. In comparison with the genetic algorithm analysis for conventional power system stabilizer （CPSS）， this analysis has better control effect.

Keywords： genetic algorithm； NARMA?L2 controller； nonlinear analysis； power system stabilizer

0 引 言

干擾和高增益一直影響著動態電力系統的穩定性，在各種操作條件和配置下都會出現低頻振蕩，限制了電力傳輸能力和系統的分解[1]。電力系統穩定器（PSS）可用于抑制勵磁系統的輔助控制信號產生的低頻振蕩，有助于提高電力系統的穩定性[2]。傳統電力系統穩定器的設計多以電力系統的線性化模型為基礎，并廣泛應用于相位補償技術和傳統電力系統穩定器（CPSS）參數的計算[3]。PSS用來改進小信號振蕩和電力系統中長傳輸線路的動態穩定性，生成高增益和速效勵磁的系統單元[4?5]。

本文對單機無窮大電力系統進行增強分析，分析發電機主磁場繞組和阻尼繞組的動態模型。基于非線性自回歸平移神經網絡的PSS控制器已經在非線性動力學領域發展起來。基于CPSS和NARMA?L2 PSS的遺傳算法已經應用于不同運行條件下的電力系統和非線性動力系統中，用來對各種干擾信號和系統故障進行測試[6]。本文提出一種新的非線性自回歸移動平均控制器主要用于改進低頻振蕩和提高長輸電線路電力系統的動態穩定性，能得到較好的控制效果。

1 電力系統模型分析

SMIB模型主要由同步發電機勵磁系統和電力系統穩定器組成，用來評估電力系統穩定器的性能，并通過傳輸線連接到無窮大系統中。同步發電機勵磁系統用非線性方程表示[7]，可以分解為式（1）～式（9）。其中，和分別為發電機端電壓和無窮母線電壓；和分別是傳輸線路電抗和變壓器電抗。

（1）

（2）

（3）

（4）

勵磁系統可以表示為：

（5）

電轉矩可表示為：

（6）

其中，可分別表示為：

（7）

（8）

（9）

（10）

（11）

2 NARMA?L2控制器設計

人工神經網絡（ANN）控制器可以用來改善非線性控制系統的性能。它不同于傳統的控制器，不需要精確的數學模型，但在穩定時間、延遲時間、尖峰值和魯棒性等時間響應參數方面能得出更好的測量結果[8?9]，再用不同的方法來調試ANN控制器后最終確定一組合適的權數[10]。

NARMA?L2控制器的執行通常分為兩個階段：第一階段是識別階段，通過產生的輸入輸出數據來控制神經網絡模型的發展；第二階段是控制器設計，用神經網絡控制器開發神經網絡模型。該神經網絡識別模型通過使用非線性乘法實現非線性系統到線性系統的轉換。圖1為系統識別階段圖，由兩組輸出模型組成，分別是模型延遲輸出值和控制器延遲輸出值。模型識別公式可以表示為：

（12）

式中：是系統輸入；是系統輸出；是系統延遲。

識別階段中為了逼近非線性函數要對神經網絡進行反向傳播訓練。如果該系統按照期望的參考軌跡運行，則非線性控制器可以寫成：endprint

（13）

使用反向傳播訓練算法可以確定最小化均方誤差函數反向傳播訓練的速度比較緩慢，并且要求模型有一定的計算能力[6，11]。為了實現更快的響應，提出了使用NARMA?L2控制器，其近似模型可表示為：

（14）

由于在同一時間用輸出來控制輸入是不現實的，控制器模型如下所示：

（15）

式中。

控制器結構如圖2所示。

3 電力系統穩定器設計

3.1 神經網絡識別碼

利用NARMA?L2 PSS對電力系統穩定性進行改善設計，用非線性自回歸移動平均模型開發出神經網絡基礎模型的識別，該系統中的速度偏差為神經網絡控制器輸出為神經網絡識別碼輸出為整個神經網絡識別的訓練過程如圖3所示。

把隨機輸入信號加載到模型中生成輸入輸出數據，從CPSS中模擬出來的隨機信號值分布在-0.04～0.04之間。神經網絡模型中有兩種輸出延遲，即控制器輸出延遲和模型輸出延遲。在此期間神經網絡識別碼的輸入為：

（16）

優化后的神經網絡識別碼如下：

（17）

式中為神經網絡NN識別碼的輸出。

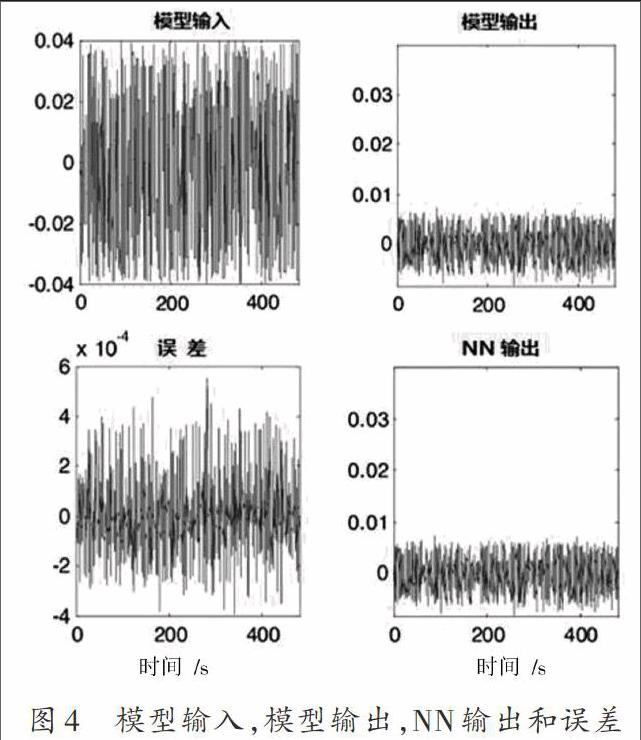
神經網絡識別碼是一個多層前饋網絡，在前饋網絡中已經開發了在隱藏層和輸出層的神經元，以及在第一層，隱藏層和輸出層的線性傳遞函數。圖4為實際模型的輸入數據，模型輸出和NN模型輸出以及兩模型之間的誤差。

3.2 神經網絡控制器

設計該神經網絡控制器的核心思想是通過改變系統的非線性狀態使系統具備動態特性。該控制器的結構如圖5所示，控制器也可由下面的等式被寫入：

（18）

4 結 論

NARMA?L2 PSS是為了改善電力系統的動態穩定性而設計的。本文利用NARMA?L2 PSS對電力系統進行非線性分析，與傳統的遺傳算法比較可以得到更好的效果。通過改變系統時間響應參數可以大幅減小功率角和轉子速度，顯著改善了低頻振蕩，快速提高了電力系統的穩定性。

參考文獻

[1] 田野，沈愛弟，王良秀，等.小型電力系統穩定性分析的改進算法及其應用[J].計算機工程，2015（1）：296?302.

[2] 厲文秀.隨機時滯電力系統穩定性分析[J].電網與清潔能源，2015（3）：29?34.

[3] 賀開華，魏建勛.大規模綜合電力系統穩定性分析[J].船電技術，2013（5）：27?30.

[4] 吳冰.電力系統穩定性分析以及電網可靠性提高方案探究[J].科技風，2010（14）：71.

[5] 浦挺.電力系統穩定性分析研究[J].科技資訊，2011（34）：111.

[6] GANDHI P R， JOSHI S K. GA based conventional and PID power system stabilizer for stability analysis of SMIB system [J]. Elixir international journal， 2011， 40： 5229?5233.

[7] 齊洪鐘，杜衛軍.電力系統穩定性分析研究[J].內蒙古石油化工，2014（12）：15?17.

[8] HASSAN L H， MOGHAVVEMI M， ALMURIB H A F， et al. Damping of low?frequency oscillations and improving power system stability via auto?tuned PI stabilizer using Takagi?Sugeno fuzzy logic [J]. International journal of electrical power and energy systems， 2012， 38（1）： 72?83.

[9] GANDHI P R， JOSHI S K. Design of PID power system stabilizer using GA for SMIB system： linear and non?linear approach [C]// Proceedings of 2011 IEEE International Conference on Recent Advancement in Electrical， Electronics and Control Engineering. [S.l.]： IEEE， 2011： 319?323.

[10] JANG J S R， SUN C T， MIZUTANI E. Neuro?fuzzy and soft computing [J]. IEEE transactions on automatic control， 2002， 42（10）： 1482?1484.

[11] ZHANG Shaoru， LUO Fanglin. An improved simple adaptive control applied to power system stabilizer [J]. IEEE transactions on power electronics， 2009， 24（2）： 369?375.endprint