基于改進同步擠壓小波變換識別信號瞬時頻率*

劉景良 ，鄭錦仰 ,鄭文婷 ，黃文金

(1.福建農林大學交通與土木工程學院 福州，350002)(2.福建工程學院土木工程學院 福州，350118)

基于改進同步擠壓小波變換識別信號瞬時頻率*

劉景良1，鄭錦仰1,鄭文婷2，黃文金1

(1.福建農林大學交通與土木工程學院 福州，350002)(2.福建工程學院土木工程學院 福州，350118)

提出了改進同步擠壓小波變換。首先，采用解析模態分解定理將非平穩響應信號分解為多個單分量信號；其次，通過頻率轉換將分解后的單分量信號從低頻區域轉換到高頻區域以提高時間分辨率；然后，對頻率重點關注區域的時頻代表值進行局部擠壓，提高時頻曲線的頻率精度；最后，通過兩個數值算例和一個拉索試驗驗證了改進同步擠壓小波變換方法的有效性和準確性。研究結果表明，改進同步擠壓小波變換能夠提高信號在特定區域內的瞬時頻率識別精度，是一種可行的時變結構參數識別方法。

改進同步擠壓小波變換；瞬時頻率；時變結構；時頻分析；非平穩信號

引 言

實際土木工程結構在承受極限荷載或長期工作荷載時，本質上是時變和非線性結構系統，其響應信號呈現非平穩性。時頻分析方法能夠有效處理非平穩信號，因而在時變結構參數識別領域受到廣泛關注，主要方法有短時傅里葉變換、二次型時頻分布[1]、小波變換[2]、以經驗模態分解為主的Hilbert-Huang變換(Hilbert-Huang transform，簡稱HHT)[3-4]、集合經驗模態分解[5]和解析模態分解(analytical modal decomposition,簡稱AMD)[6]等，其中以HHT和小波變換方法研究最為深入。HHT本質上是一種經驗的局域分析方法，它無法分離密集的模態響應，特別是模態頻率疊混的信號[7]。Yan等[8]將HHT變換與連續小波變換進行對比，結果表明小波變換在識別密集模態時優于HHT。

小波變換能夠自適應調整時窗跟頻窗大小并實現多分辨率分析，十分適合非平穩信號的分析處理。孫鵬等[9]使用Morlet小波變換識別懸索橋模型的固有頻率和阻尼比。許鑫等[10]基于狀態空間和小波理論提出了時變系統的參數識別方法。王超等[11]提出一種基于動態規劃提取信號小波脊線和瞬時頻率(instantaneous frequency,簡稱IF)的方法，該方法具有較強的抗噪性和較高的計算效率。盡管小波變換在時變結構參數識別領域中取得成功，但如何提取清晰的時頻曲線目前仍沒有得到很好的解決。Daubechies等[12]提出同步擠壓小波變換(synchrosqueezing wavelet transform,簡稱SST)，通過重組小波變換后的時頻圖獲得較高頻率精度的時頻曲線。劉景良等[13]將同步擠壓小波變換引入土木工程領域，識別了時變結構響應信號的瞬時頻率。但是，同步擠壓小波變換方法只能處理信號頻率不變時尺度方向的擴散，對于時間維度上的擴散無能為力。Li等[14]針對標準同步擠壓算法存在小波系數擴散的問題，提出了廣義的同步擠壓小波變換算法。該方法能夠獲得較高精度的時頻曲線，但前提條件是響應信號的數學解析表達式必須已知，而實際工程中的響應信號并不滿足這一先決條件。汪祥莉等[15]針對混沌干擾背景下多個諧波信號的提取問題，提出一種基于同步擠壓小波變換的諧波信號抽取方法，但該方法無法對非平穩諧波信號進行有效處理。可見，同步擠壓小波變換作為一種以小波變換為基礎的全新的時頻分析方法，目前雖有相關的理論研究，但其算法的改進和在實際工程中的應用還十分缺乏。因此，如何對同步擠壓小波變換進行改進并使其能夠同時處理時間和頻率兩個維度方向的擴散是一個急需解決的關鍵問題。

筆者提出的改進同步擠壓小波變換方法首先通過解析模態分解定理將多分量響應信號分解為單分量信號；其次，通過頻率轉換將原始信號的瞬時頻率值從低頻區域轉換到高頻區域，達到了提高時間分辨率的目的；然后，對重點關注區域的時頻代表值進行重組，提高了該區域瞬時頻率識別值的頻率精度。改進同步擠壓小波變換摒棄了標準同步擠壓小波變換沿整個頻率軸對連續小波變換后的時頻代表值進行擠壓的做法，對重點區域的時頻代表值進行時頻重組[16]，使該區域的頻率精度得到提高。因此，改進同步擠壓小波變換同時提高了重點關注區域瞬時特征參數在頻率和時間兩個維度上的識別精度。為驗證該方法的有效性，將其應用于兩個多分量信號數值算例和一個拉索試驗。結果表明，改進同步擠壓小波變換能夠有效提取非平穩響應信號的瞬時頻率，是一種可行的時變結構參數識別方法。

1 標準同步擠壓小波變換

一個典型的多分量信號可以表達為N個本征函數和一個余量之和。

(1)

其中：xi(t)=Ai(t)cos(φi(t))為第i個本征函數，其幅值的變化率A′(t)遠小于相位對時間的變化率φ′(t)；r(t)為噪聲或者觀測誤差。

對于給定的母小波函數ψ(t)，信號x(t)的連續小波變換定義為

(2)

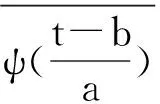
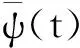
(3)

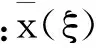
通過對小波系數求導，初步求得式(4)的瞬時頻率為

(4)

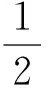
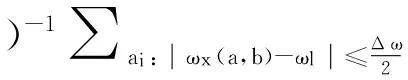
(5)

若尺度a及頻率ω為連續變量，式(5)可改寫為

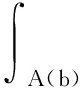
(6)

2 改進同步擠壓小波變換

2.1AMD定理提取多分量信號

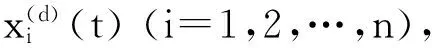
(7)

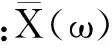
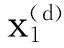
(8)

si(t)=sin(ωbit)H[x(t)cos(ωbit)]-

cos(ωbit)H[x(t)sin(ωbit)]

(i=1,2,…,n-1)

(9)

其中：H[·]為希爾伯特算子。

在進行AMD分解之前，對信號進行連續小波變換，得到其小波量圖并以此作為選取截止頻率的依據，從而將兩個截止頻率之間的分量信號提取出來。

2.2 頻率轉換

標準同步擠壓小波變換提高了信號瞬時頻率的頻率精度，卻沒有提高其時間精度。為了獲取更高的時間分辨率，頻率轉換把信號的瞬時頻率從低頻區域轉到高頻區域。

單分量信號x(t)=cos[2π(f1+f0)t+sin2πf0t]可改寫為

x(t)=cos[2πf1t+sin2πf2t]cos(2πf0t)-

sin[2πf1t+sin2πf2t]sin(2πf0t)

(10)

根據式(10)，給定信號x(t)的頻率轉換定義為

x*(t)=x(t)cos(2πf0t)-H[x(t)]sin(2πf0t)

(11)

其中：H[·]為希爾伯特算子。

信號x*(t)的瞬時頻率ω*(a,b)為

ω*(a,b)=ω(a,b)+ω0

(12)

其中：ω(a,b)為信號x(t)通過時頻分析方法得出的瞬時頻率；ω0=2πf0。

在改進同步擠壓小波變換算法中，為得到更好的時間分辨率，需預先設定f0>0，即正頻率轉換。若f0<0，則為負頻率轉換，目的是為了得到更好的頻率分辨率，將信號的中心頻率從高頻轉到低頻。

2.3 時頻重組

在時頻重組階段，改進同步擠壓小波變換在重點關注頻率區間[fm,fM]內對時頻代表值進行擠壓，提高了瞬時頻率識別精度，同時也降低了計算量。定義兩個中間變量lfm,lfM分別為

(13)

通過改進同步擠壓小波變換得到的頻率序列為

(14)

其中：n為重點關注區域離散頻率點的個數。

得到信號的圓頻率序列為

用ωis替換式(5)的ωl，得到同步擠壓小波變換系數值Tx(ωis,b)為

(16)

2.4 改進同步擠壓小波變換算法流程

改進同步擠壓小波變換算法通過AMD定理分解多分量信號、頻率轉換和時頻重組，同時提高了重點關注區域瞬時特征參數在頻率和時間兩個維度上的識別精度，其計算流程如圖1所示。

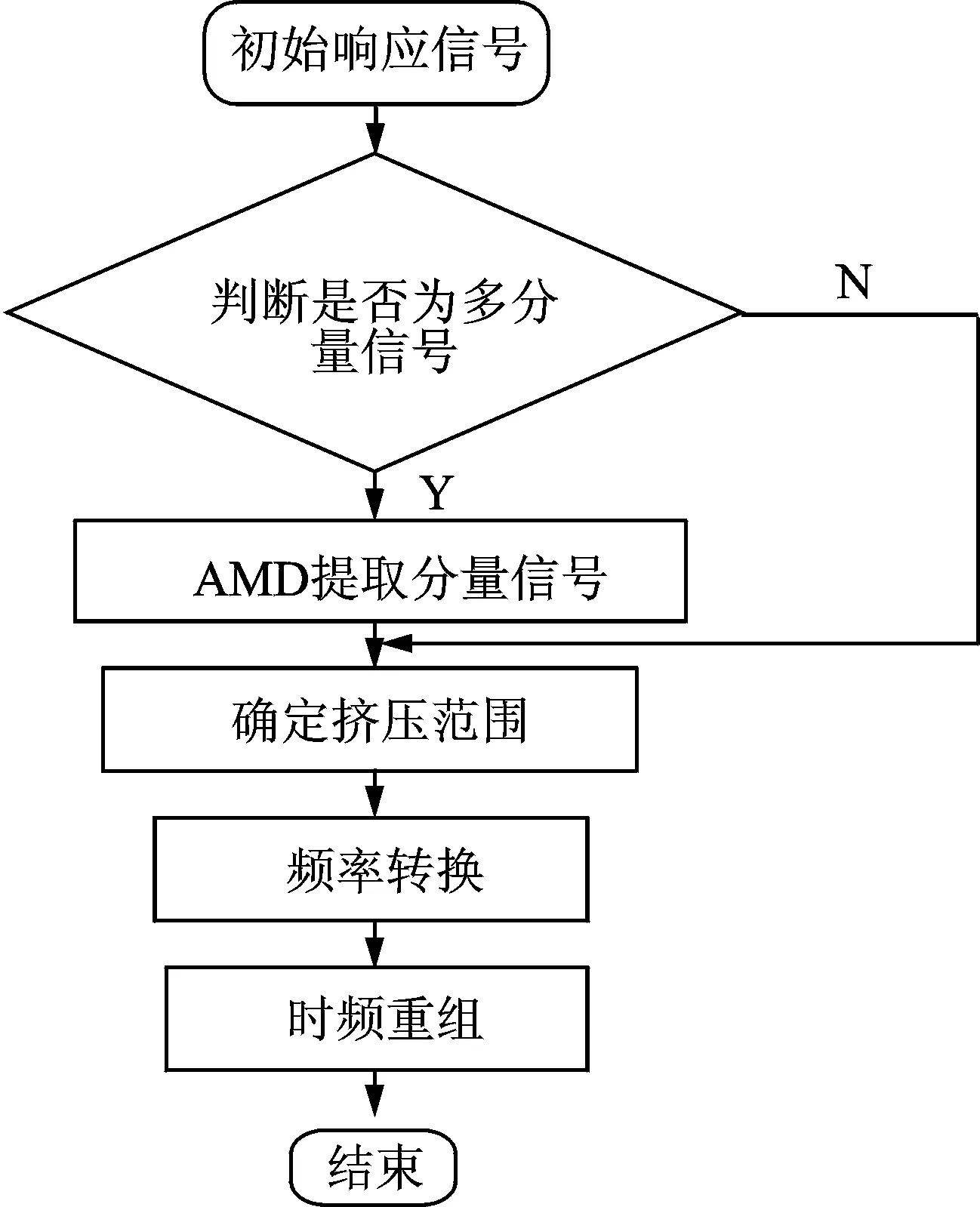
圖1 改進同步擠壓小波變換算法流程圖Fig.1 The flowchart of the improved synchrosqueezing wavelet transform algorithm

由圖1可知，改進同步擠壓小波變換算法共分為5個步驟。

1) 判斷初始響應信號是否為多分量信號。將響應信號進行連續小波變換并得到其小波量圖。從小波量圖中可以觀察得出分量信號的數目及每個分量信號瞬時頻率的大致范圍，并以此作為選取截止頻率的依據。

2) AMD定理提取分量信號。在選取合適的截止頻率之后，可通過AMD及其拓展定理將多分量信號中的各個分量信號解析地提取出來。

3) 確定擠壓范圍。單分量信號的擠壓范圍可根據小波量圖中的頻率分布情況以及分量信號的截止頻率進行選取。

4) 頻率轉換。將提取出的單分量信號進行周期延拓以減小端點效應對信號的影響，然后確定轉換頻率，并對周期延拓后的信號進行正頻率轉換以提高時域分辨率。

5) 時頻重組。對完成頻率轉換步驟的單分量信號進行連續小波變換，將小波變換系數進行時頻重組得到改進同步擠壓小波變換系數并提取其瞬時頻率，根據式(12)將瞬時頻率轉換到原來位置。

3 數值算例驗證

為驗證改進同步擠壓小波變換的有效性和準確性，考慮多分量調頻(frequency modulated,簡稱FM)信號，即

x(t)=x1(t)+x2(t)

(17)

其中：信號采樣頻率為1 kHz；采樣時間為1 s；x1=sin[2π(100t+t2)]；x2=sin[2π(150t+20t3)]。

兩個分量信號所對應的瞬時頻率理論值分別為f1(t)=100+2tHz，f2(t)=150t+60t2Hz。為考慮信號噪聲影響，對信號添加20%水平的高斯白噪聲，噪聲強度由信噪比定義(單位dB)。

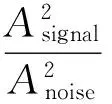
(18)

其中：Asignal和Anoise分別為信號和噪聲的均方根值；噪聲水平是指Asignal與Anoise之間的比值。

添加20%水平噪聲后的多分量調頻信號如圖2所示。選用復Morlet小波對含噪多分量調頻信號進行連續小波變換，得到如圖3所示的小波量圖。由圖3可知，分量信號x1(t)的瞬時頻率集中在100 Hz附近，且呈線性變化，而分量信號x2(t)的瞬時頻率分布范圍為150～250 Hz，呈拋物線變化趨勢。

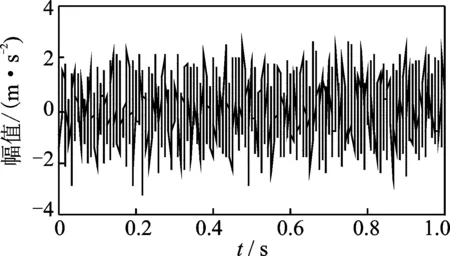
圖2 多分量調頻信號Fig.2 Simulated multi-component FM signal with 20% Gauss white noise

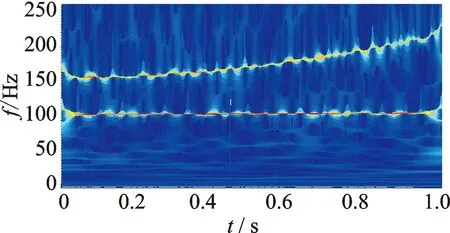
圖3 添加20%水平噪聲的多分量調頻信號小波量圖Fig.3 Wavelet scalogram of the multi-component FM signal with 20% Gauss white noise

采用AMD定理提取的兩個分量信號及其相應的理論值如圖 4所示。由于20%水平噪聲的影響，使提取的信號與理論值產生一定的偏差，但二者總體上仍十分吻合。設定f0=100Hz，對提取的分量信號進行改進同步擠壓小波變換，識別的瞬時頻率如圖5所示。為驗證改進同步擠壓小波變換識別瞬時頻率的準確性，圖5同時給出了多分量調頻信號瞬時頻率理論值和基于標準同步擠壓小波變換的識別值。可以看出，相比標準同步擠壓小波變換，改進同步擠壓小波變換識別的瞬時頻率曲線較為光滑，且與理論值更加吻合，具有更好的分辨率。但是改進同步擠壓小波變換以同步擠壓小波變換為基礎，因此端點效應依然存在，但所受影響要小得多。

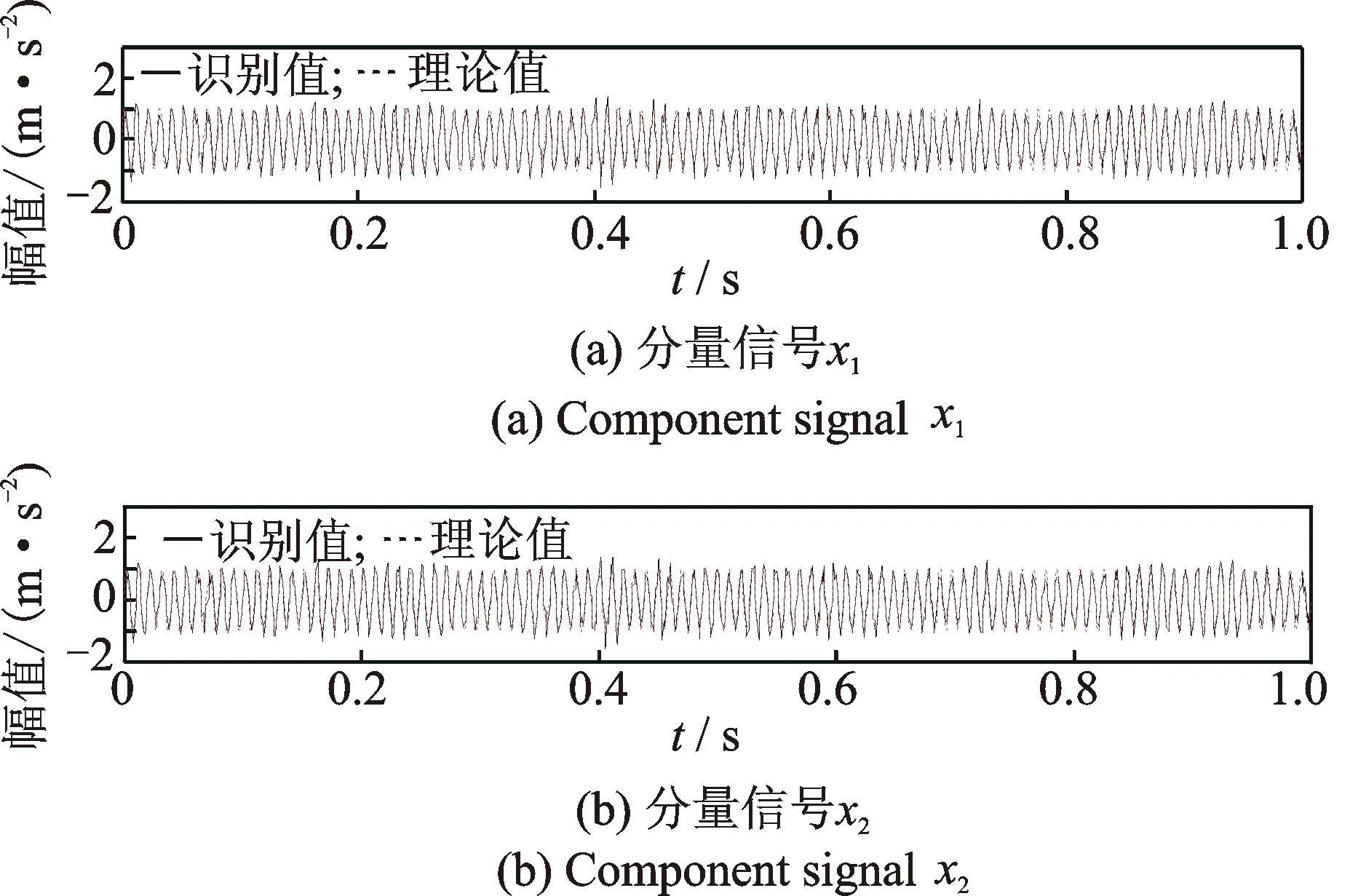
圖4 AMD提取的單分量信號Fig.4 Mono-components extracted by AMD theorem

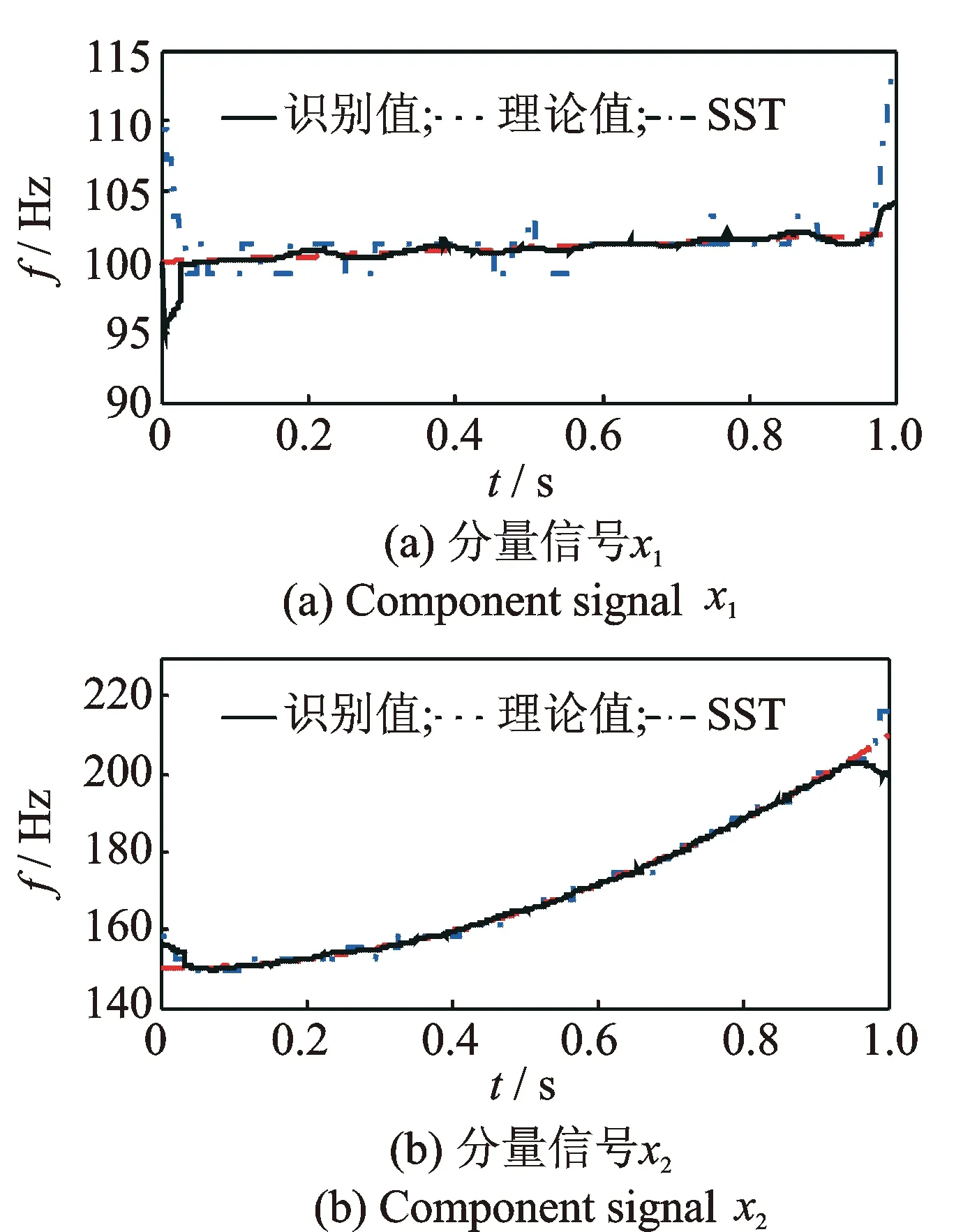
圖5 改進同步擠壓小波變換識別的瞬時頻率Fig.5 IF identified by improved synchrosqueezing wavelet transform

為量化瞬時頻率的識別精度，采用瞬時頻率在整個時間歷程內的均方根值作為精度指標(index of accuracy,簡稱IA) 。IA值越小，說明識別值與理論值越接近。

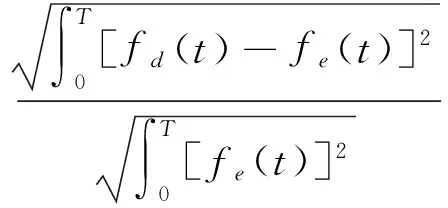
(19)

其中：fd(t)為瞬時頻率識別值；fe(t)為瞬時頻率理論值。

表1為同步擠壓小波變換法和改進擠壓小波變換方法識別瞬時頻率的精度指標IA。IAa和IAb分別為信號x1與x2的瞬時頻率識別精度指標。由表1可知，針對多分量調頻信號，改進同步擠壓小波變換的識別效果優于基于標準同步擠壓小波變換的瞬時頻率識別方法。

表1 多分量調頻信號瞬時頻率識別精度指標IATab.1 IA of instantaneous frequency identification of multi-component FM signal %

為進一步驗證改進同步擠壓小波變換識別多分量信號的有效性和準確性，定義一個由兩個瞬時頻率呈余弦變化的調頻分量組成的多分量非平穩信號y(t)為

y(t)=y1(t)+y2(t)

(20)

其中：y1(t)=5cos[2πt+0.8sin(0.4πt)]；y2(t)=10cos[3.6πt+0.5sin(0.5πt)]。

兩個分量信號的瞬時頻率分別為f1(t)=1.0+0.16cos(0.4πt)Hz，f2(t)=1.8+0.125×cos(0.5πt)Hz。采樣頻率為100 Hz，采樣時間為50 s。添加20%水平噪聲后的y(t)如圖6所示。

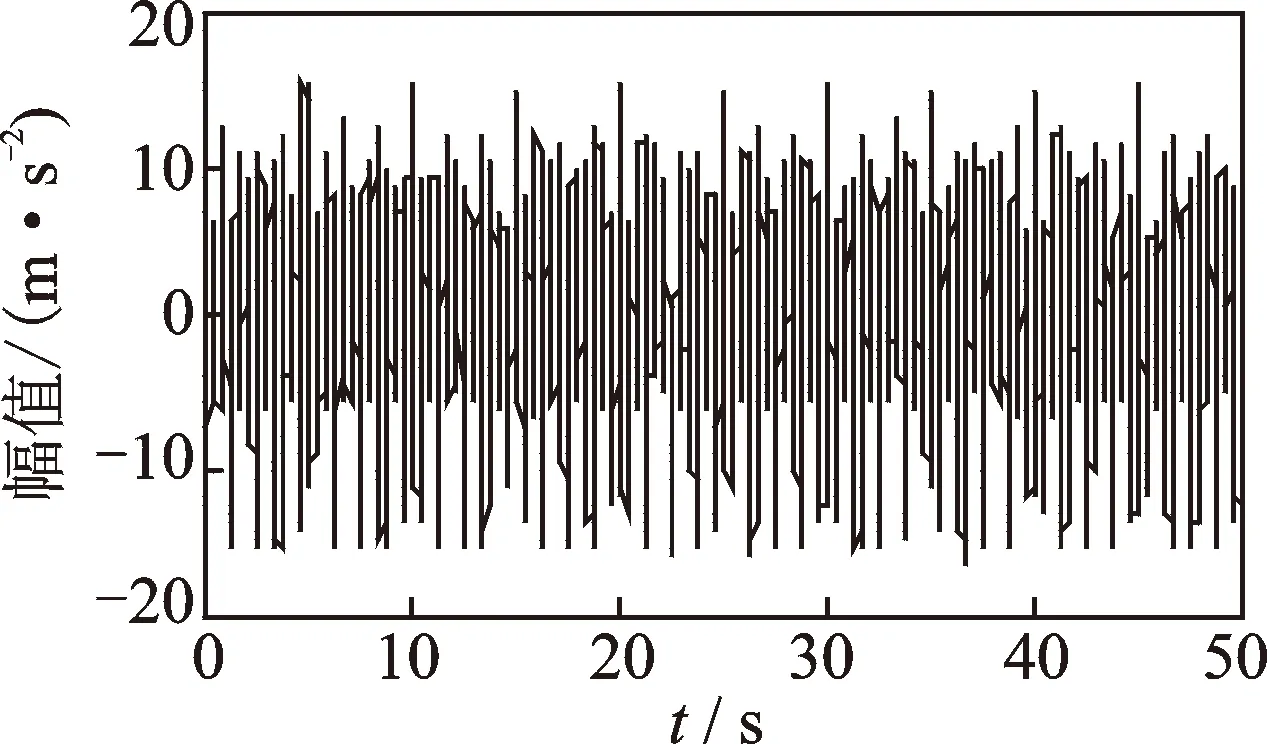
圖6 多分量非平穩信號Fig.6 Simulated multi-component non-stationary signal

選用復Morlet小波對含噪多分量非平穩信號進行連續小波變換，得到如圖7所示的小波量圖。可見，分量信號y1(t)和y2(t)的瞬時頻率大致呈正弦變化。采用AMD定理提取的單分量信號如圖8所示。圖8中提取的單分量信號在整個時間歷程內均與理論值基本一致，但是由于噪聲的影響，使得提取值在某些峰值處出現不吻合的情況。

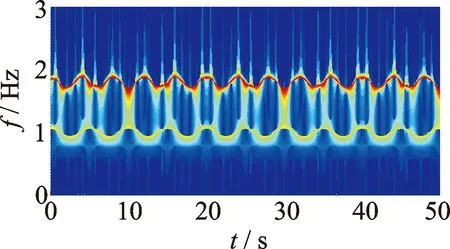
圖7 添加20%水平噪聲的多分量非平穩信號小波量圖Fig.7 Wavelet scalogram of multi-component non-stationary signal with 20% Gauss white noise

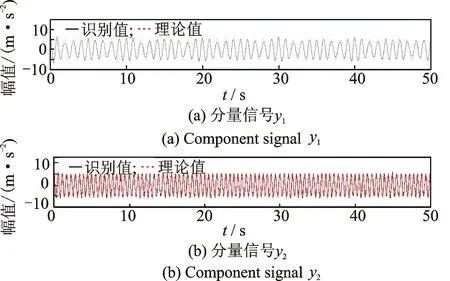
圖8 AMD提取的單分量信號

Fig.8 Mono-components extracted by AMD theorem

設定f0=30Hz，對AMD提取的單分量信號采用改進同步擠壓小波變換算法識別，如圖9所示。可見，改進同步擠壓小波變換識別的瞬時頻率與理論值基本保持一致，只是在峰值處產生些許誤差。與標準同步擠壓小波變換相比，改進同步擠壓小波變換識別結果更為光滑和準確。改進同步擠壓小波變換算法的端點效應依然存在，但影響較小。

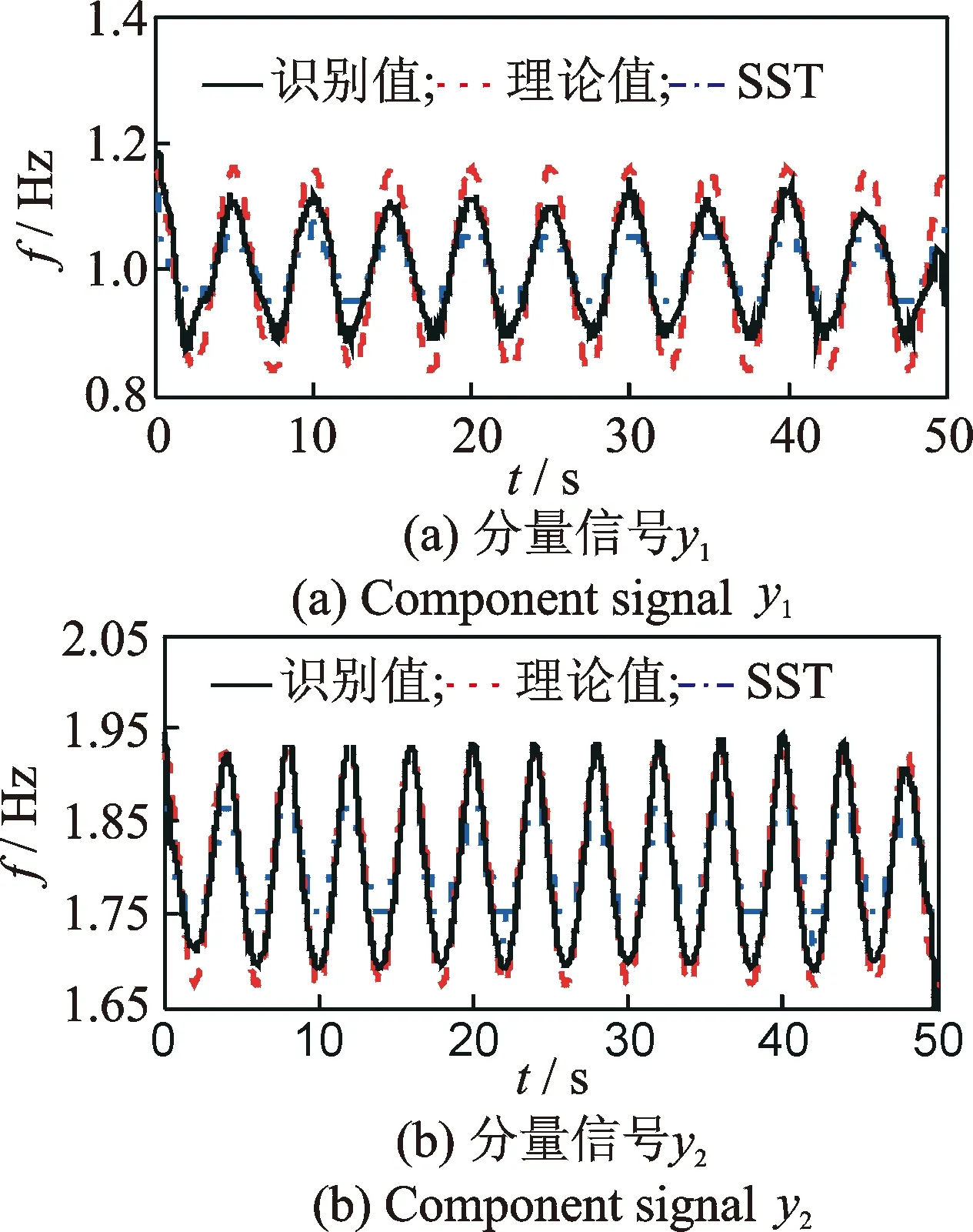
圖9 改進同步擠壓小波變換識別的瞬時頻率Fig.9 IF identified by improved synchrosqueezing wavelet Transform

基于兩種方法的瞬時頻率識別精度指標IA值如表2所示。由表2可知，改進同步擠壓小波變換瞬時頻率識別結果明顯優于標準同步擠壓小波變換識別結果。

表2 多分量非平穩信號瞬時頻率識別精度指標IATab.2 IA of instantaneous frequency identification of multi-component non-stationary signal %

4 拉索試驗驗證

為驗證改進擠壓小波變換的有效性和準確性，設計一個時變拉索結構試驗。試驗拉索為一根7φs5的鋼絞線。兩錨固點間的索長為4.55 m，將加速度傳感器豎向安裝在拉索中部。索的一端用反力架錨固，另一端采用電液伺服加載系統的作動器施加拉力。首先，對索施加一定的預拉力，隨后連續改變索的拉力，使索的剛度隨時間發生變化，從而導致索的固有頻率隨之改變。在改變索力的同時，用力錘敲擊拉索，采集索的豎向加速度沖擊響應，采樣頻率為600 Hz。試驗裝置如圖10所示。試驗過程中采用了兩個工況：即索拉力線性變化和正弦變化。為了與識別結果進行比較，筆者采用“凍結法[11]”，即假定在很小的時間間隔內結構參數保持不變，通過求解系統振動方程的特征值和特征向量近似得到拉索瞬時頻率的理論值。本次試驗分析中，頻率主要采用一階模態頻率，即基頻。

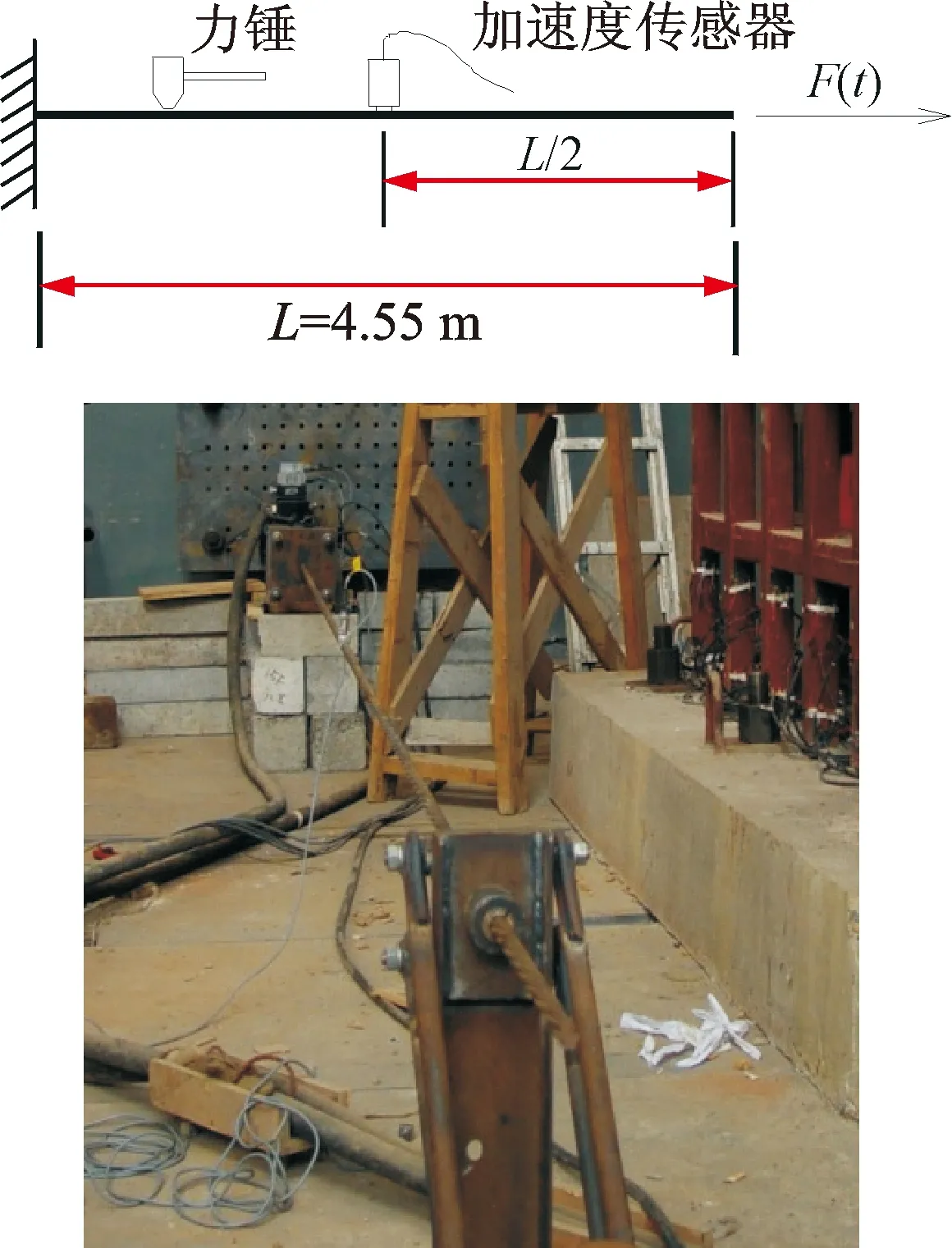
圖10 試驗裝置圖Fig.10 Cable test setup

4.1 拉力線性變化時索的瞬時頻率識別

試驗時設定索的拉力從20 kN開始，以1.67 kN/s的速率線性加載，同時采集索的沖擊加速度響應，采樣時間為7 s，采樣頻率為600 Hz。測得的加速度響應信號如圖11所示。索的拉力變化曲線如圖12所示。

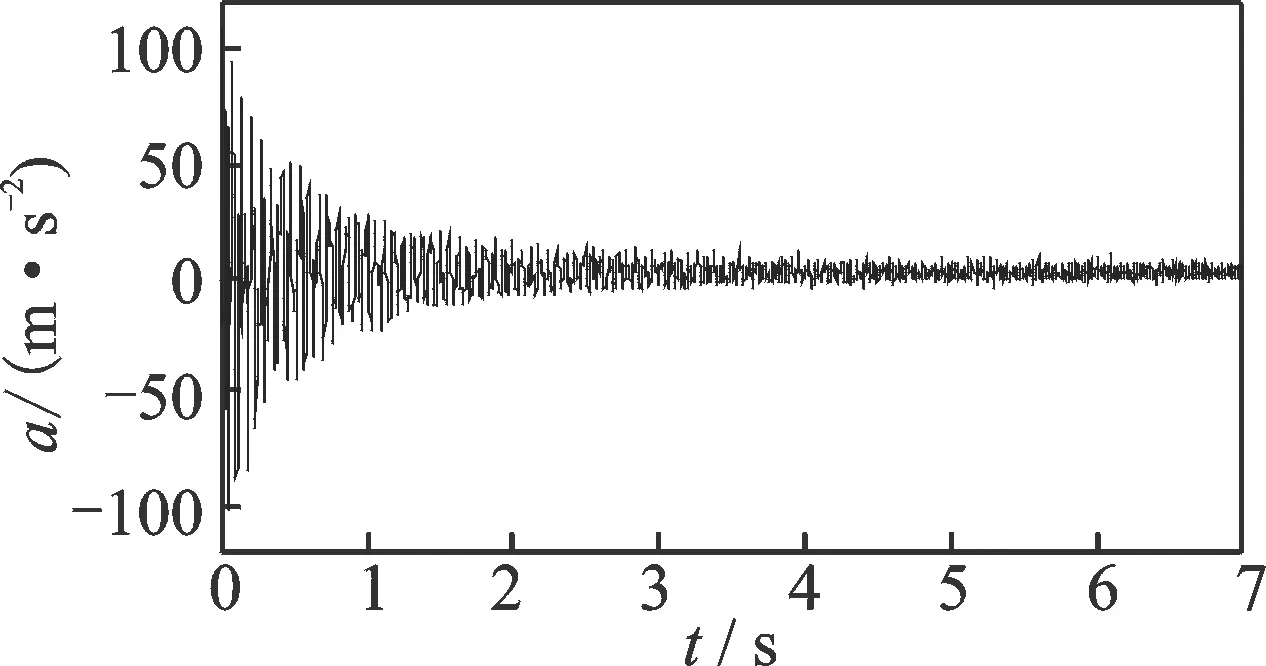
圖11 拉力線性變化時索的加速度響應Fig.11 Measured cable acceleration responses with linearly varying cable tension force

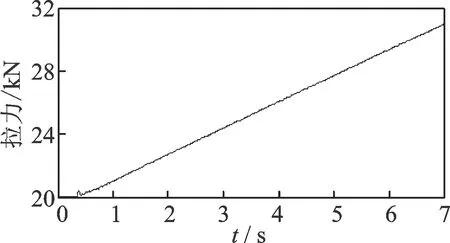
圖12 實測的線性變化拉力Fig.12 Measured cable tension forces with linear variation

如圖13所示，對實測加速度響應信號進行復Morlet小波變換，發現實測信號的小波脊線大致呈線性變化。如圖14所示，采用AMD定理提取實測信號的基頻分量。設定f0=30 Hz，對基頻分量進行改進同步擠壓小波變換，識別的拉索瞬時頻率結果如圖15所示。可見，相比標準同步擠壓小波變換，改進同步擠壓小波變換識別的瞬時頻率曲線擁有更高的光滑程度，且與瞬時頻率理論值更為接近，只是在信號的開始和結束階段出現一些偏離。這主要是因為端點效應所致。此外，由于加速度響應信號末端幅值較小，因而信噪比低，在一定程度上影響了瞬時頻率識別結果。表3中的IA結果也表明，改進同步擠壓小波變換方法識別瞬時頻率的準確性相對較高，優于標準同步擠壓小波變換。

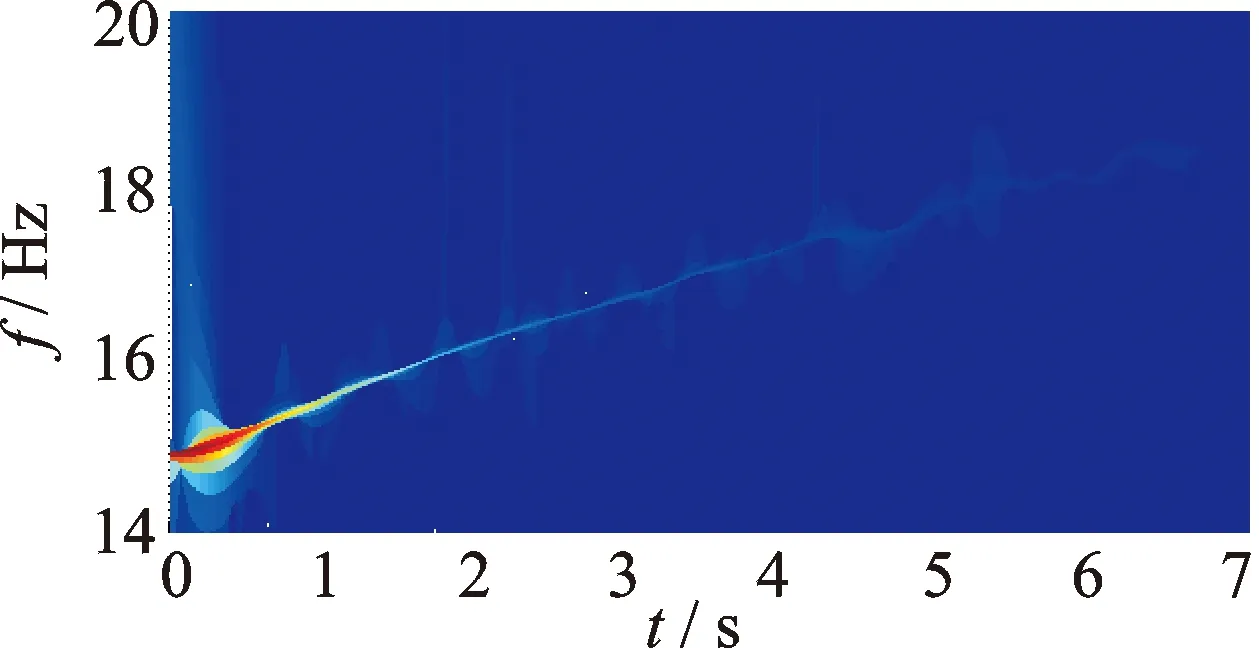
圖13 實測響應信號小波量圖Fig.13 Wavelet scalogram of measured cable acceleration responses

圖14 AMD提取的基頻分量信號Fig.14 The fundamental modal frequency component signal extracted by AMD theorem

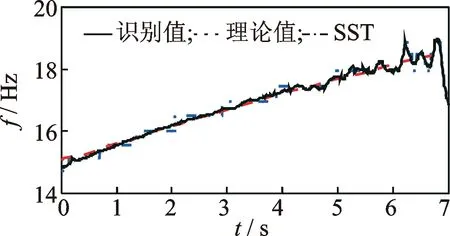
圖15 拉力線性變化時索的瞬時頻率識別結果Fig.15 Identified instantaneous frequency with linearly varying cable tension force

表3 拉力線性變化時索的瞬時頻率識別精度指標IATab.3 IA of instantaneous frequency identification with linearly varying cable tension force %

4.2 拉力正弦變化時索的瞬時頻率識別

試驗時索的拉力呈正弦曲線變化，變換幅度為±4 kN。實測加速度響應信號和索拉力變化曲線分別如圖16，17所示。對實測加速度響應信號進行復Morlet小波變換，其小波量圖如圖18所示。由圖18可知，實測信號的小波脊線大致呈正弦變化。通過AMD將實測信號基頻分量提取出來，如圖19所示。設定f0=20Hz，將改進同步擠壓小波變換與標準同步擠壓小波變換瞬時頻率識別結果進行比較，如圖20所示。從圖20可知，由于端點效應以及低信噪比的影響，改進同步擠壓小波變的瞬時頻率識別結果出現了一定的偏差，但瞬時頻率的正弦變化趨勢與理論頻率基本保持一致。兩種方法的瞬時頻率識別精度指標IA如表4所示。由表4可知，改進同步擠壓小波變換精度指標值比同步擠壓小波變換的相應值低1.2%，再次證明改進同步擠壓小波變換提高了瞬時頻率的識別精度。

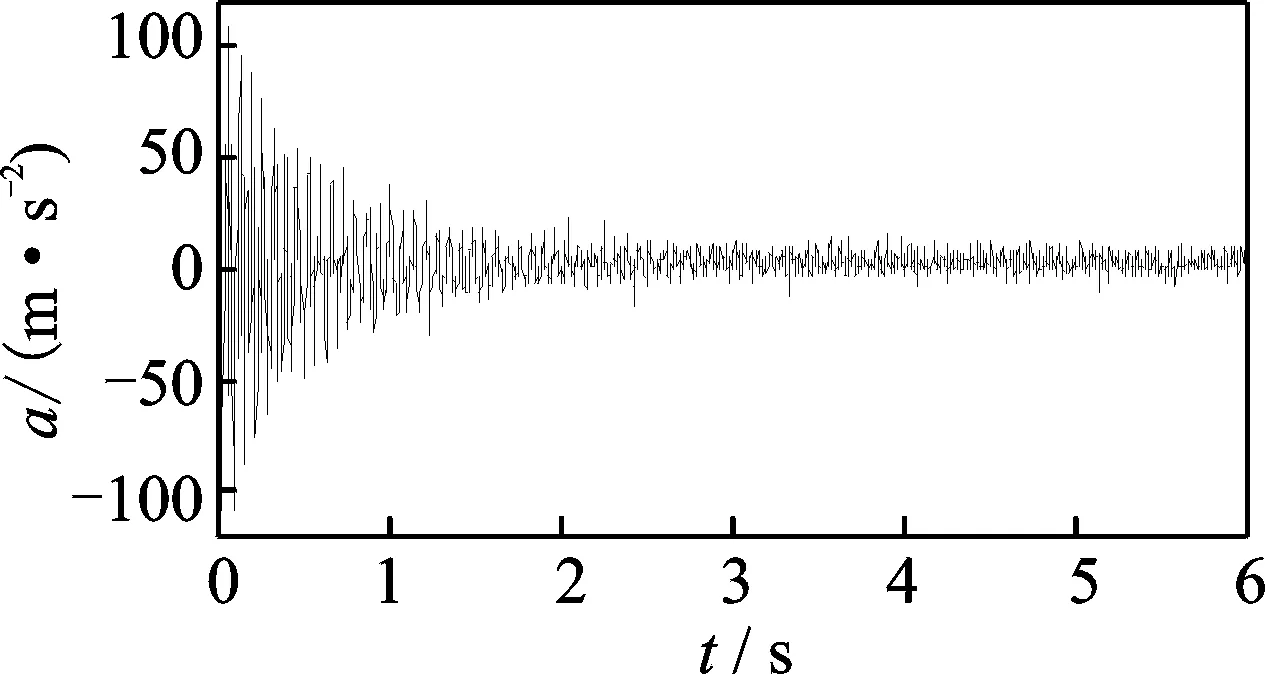
圖16 拉力正弦變化時索的加速度響應Fig.16 Measured cable acceleration responses with sinusoidal varying tension force

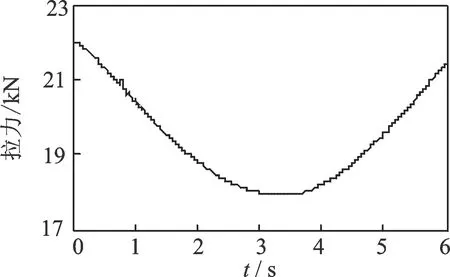
圖17 實測的正弦變化拉力Fig.17 Measured cable tension force with sinusoidal variation

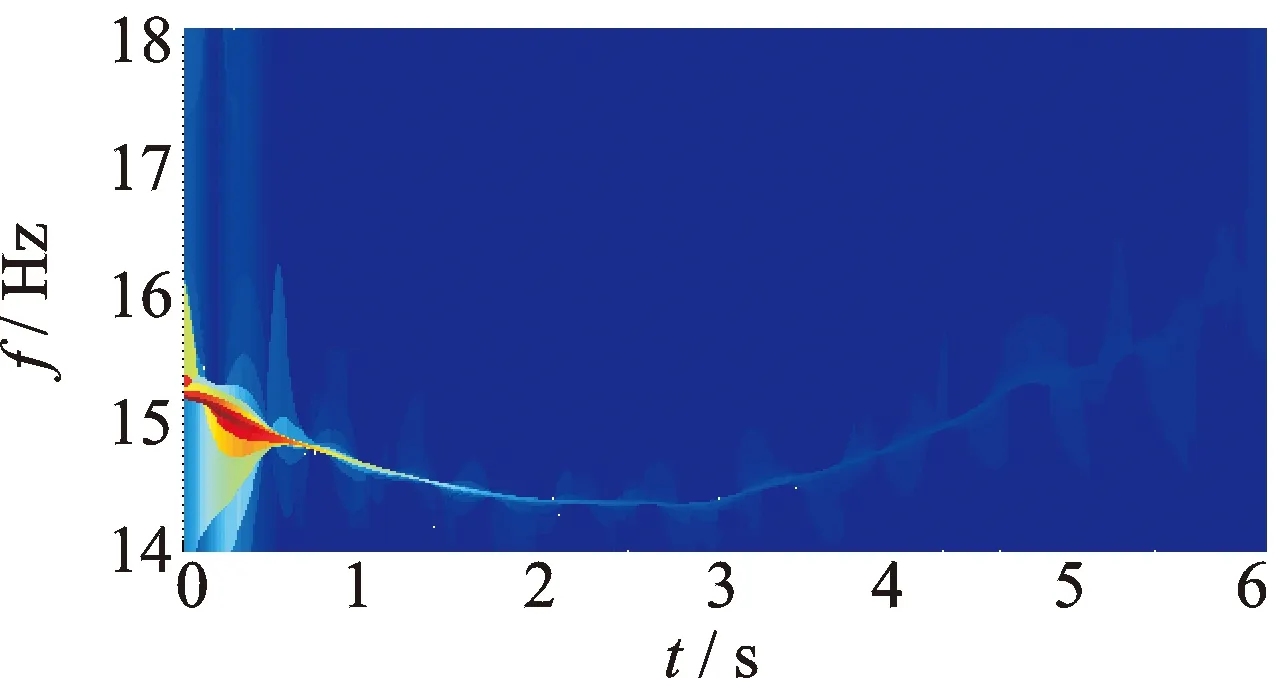
圖18 實測響應信號小波量圖Fig.18 Wavelet scalogram of measured cable acceleration responses

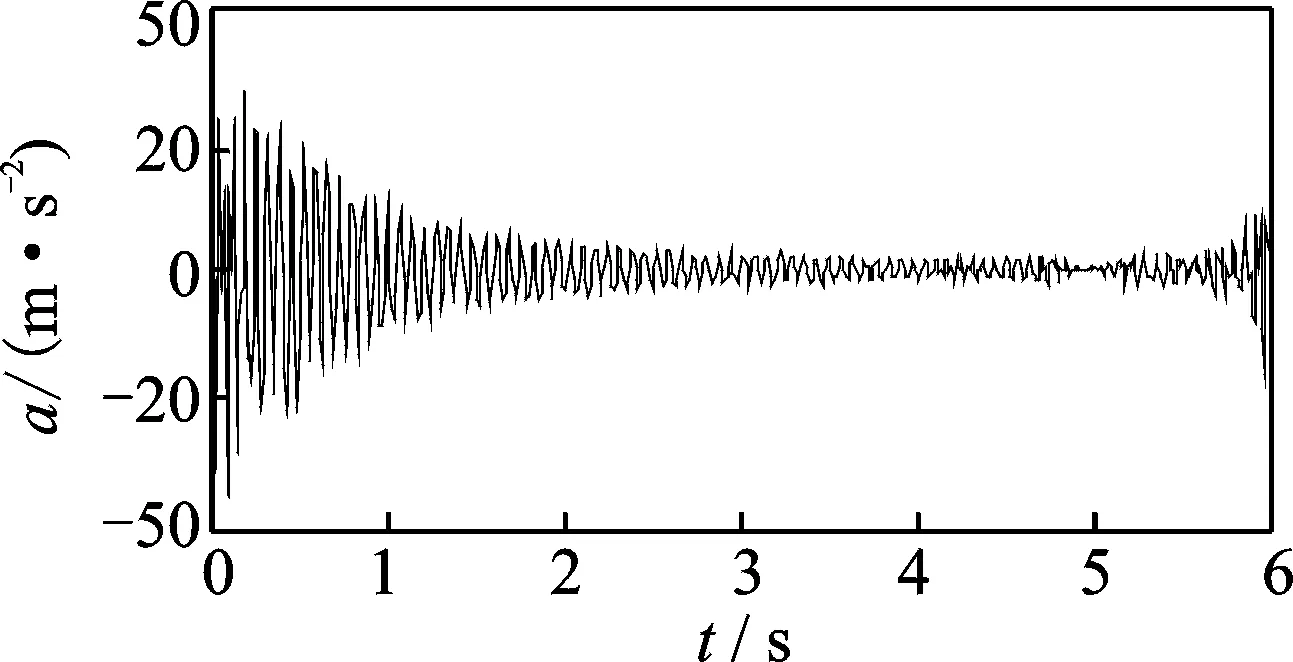
圖19 AMD提取的基頻分量信號Fig.19 The fundamental modal frequency component signal extracted by AMD theorem

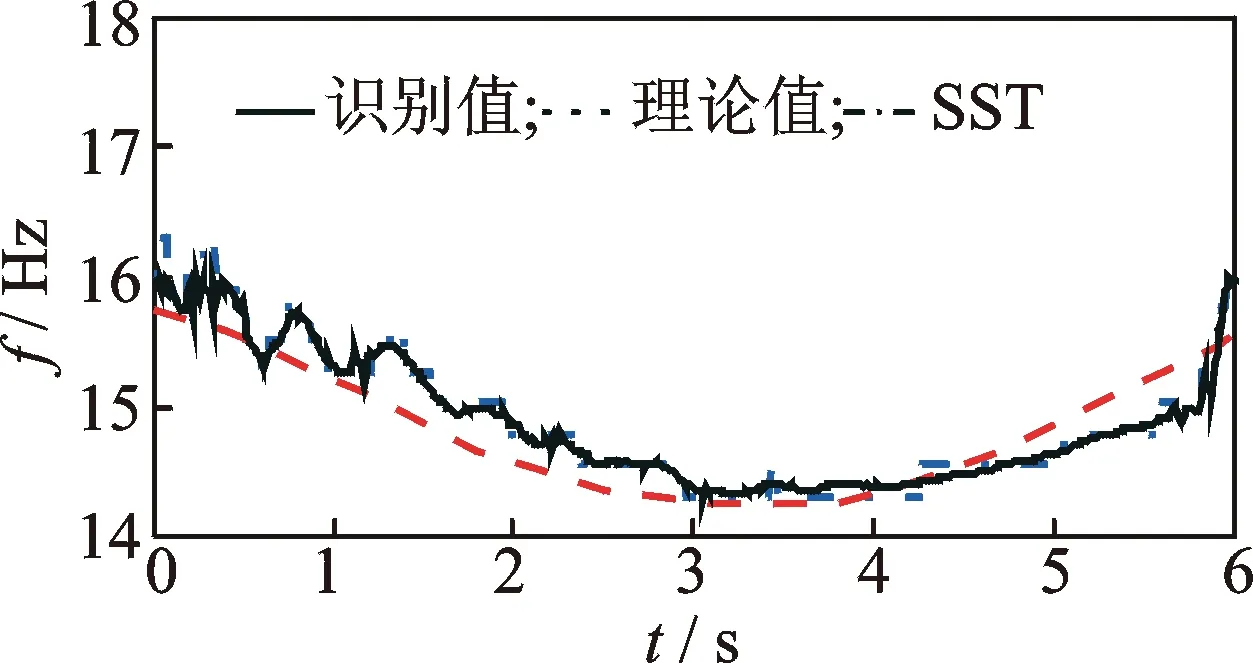
圖20 瞬時頻率識別值比較Fig.20 Identified instantaneous frequency with sinusoidal varying cable tension force

表4 拉力正弦變化時索的瞬時頻率識別精度指標IATab.4 IA of instantaneous frequency identification with sinusoidal varying cable tension force %

5 結 論

1) 改進同步擠壓小波變換能夠有效地識別噪聲干擾下多分量信號的瞬時頻率，且識別效果優于標準同步擠壓小波變換。

2) 改進同步擠壓小波變換能夠有效地識別實測響應信號的瞬時頻率。當索的拉力線性變化時，識別出的瞬時頻率與理論結果非常接近；當拉力正弦變化時，識別出的瞬時頻率與理論識別結果也比較吻合。

3) 端點效應在一定程度上影響基于改進同步擠壓小波變換的瞬時頻率識別效果，但影響小于標準同步擠壓小波變換。

[1] Wang Zhongren,Lin Jun.Time-frequency analysis for complex time-varying signals based on Wigner-Ville distribution[J].Acta Electronica Sinica,2005,33(12):2239-2241.

[2] Hou Z,Hera A,Shinde A.Wavelet-based structural health monitoring of earthquake excited structures[J].Computer-Aided Civil and Infrastructure Engineering,2006,21:268-279.

[3] Huang N E,Shen Z,Long S R.A new view of nonlinear water waves:the Hilbert spectrum[J].Annual Review of Fluid Mechanics,2003,31(1):417-457.

[4] 熊飛,程遠勝,劉均.基于HHT方法的時變多自由度系統的損傷識別[J].振動、測試與診斷，2008，28(2)：122-125.

Xiong Fei,Cheng Yuansheng,Liu Jun.Damage identification of time varying multi-degrees of freedom systems based on Hilbert-Huang transform[J].Journal of Vibration,Measurement &Diagnosis,2008,28(2):122-125.(in Chinese)

[5] Wu Zhaohua,Huang N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2011,1(1):1-41.

[6] Wang Zuocai,Ren Weixin,Liu Jingliang.A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction[J].Journal of Sound and Vibration,2013,332:6016-6028.

[7] Chen Genda,Wang Zuocai.A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J].Mechanical Systems and Signal Processing,2012,28(2):258-279.

[8] Yan B,Ayaho M.A comparative study of modal parameter identification based on wavelet and Hilbert-Huang transforms [J].Computer-Aided Civil and Infrastructure Engineering,2006,21:9-23.

[9] 孫鵬,丁幼亮,李愛群，等.利用Morlet小波變換識別懸索橋模型模態參數[J].振動、測試與診斷，2012， 32(2)：238-243.

Sun Peng,Ding Youliang,Li Aiqun,et al.Modal identification for suspension-bridge model using morlet wavelet transform[J].Journal of Vibration,Measurement &Diagnosis,2012,32(2):238-243.(in Chinese)

[10] 許鑫，史治宇.狀態空間下基于小波變換的時變系統參數識別[J].振動工程學報，2010，23(4)：415-419.

Xu Xin,Shi Zhiyu.Parameter identification of time-varying system based on state space and wavelet transform method [J].Journal of Vibration Engineering,2010,23(4):415-419.(in Chinese)

[11] 王超，任偉新，黃天立.基于復小波變換的結構瞬時頻率識別[J].振動工程學報,2009,22(5):492-496.

Wang Chao,Ren Weixin,Huang Tianli.Instantaneous frequency identification of a structure based on complex wavelet transform[J].Journal of Vibration Engineering,2009,22(5):492-496.(in Chinese)

[12] Daubechies I,Lu Jianfeng,Wu H T.Synchrosqueezed wavelet transforms:an empirical mode decomposition-like tool[J].Applied and Computational Harmonic Analysis,2011,30:243-261.

[13] 劉景良，任偉新，王佐才，等.基于同步擠壓小波變換的結構瞬時頻率識別[J].振動與沖擊，2013，32(18)：37-42.

Liu Jingliang,Ren Weixin,Wang Zuocai,et al.Instantaneous frequency identification based on synchrosqueezing wavelet transformation[J].Journal of Vibration and Shock,2013,32(18):37-42.(in Chinese)

[14] Li Chuan,Liang Ming.Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform[J].Mechanical Systems and Signal Processing,2012,26 (1):205-217.

[15] 汪祥莉，王斌，王文波，等.混沌干擾中基于同步擠壓小波變換的諧波信號提取方法[J].物理學報，2015，64(10)：11-20.

Wang Xiangli,Wang Bin,Wang Wenbo,et al.Harmonic signal extraction from chaotic interference based on synchrosqueezed wavelet transform[J].Acta Physica Sinica,2015,64(10):11-20.( in Chinese)

[16] Cao Hongrui,Xi Songtao,Chen Xuefeng,et al.Zoom synchrosqueezing transform and iterative demodulation:Methods with application [J].Mechanical Systems and Signal Processing,2016,72-73:695-711.

10.16450/j.cnki.issn.1004-6801.2017.04.028

* 國家自然科學基金資助項目(51608122)；福建省自然科學基金青年科技人才創新資助項目(2016J05111);福建省教育廳科技資助項目(JAT160330)

2016-11-07；

2017-01-25

TU311.3；TH113.1

劉景良，男，1983年11月生，博士、講師。主要研究方向為結構健康監測、橋梁振動與穩定。曾發表《基于同步擠壓和時間窗的時變結構損傷識別》(《振動工程學報》2014年第27卷第6期)等論文。 E-mail：liujingliang@fafu.edu.cn