一種基于徑向基函數的模型參考自適應控制的研究
王鑫
摘 要:文章介紹了基于RBF(徑向基函數)神經網絡的辨識,實現單神經元PID模型的自適應控制。采用RBF神經網絡,是由于其結構簡單,應用成熟,具有萬能逼近性;采用單神經元構成的PID自適應器是因為其具備適應性強,結構簡單,有學習的功能。我們通過RBF神經網絡的辨識后進行單神經元PID的自適應控制,隨時對參數進行學習與修改,以求達到所要的效果。
關鍵詞:RBF神經網絡;單神經元PID;辨識;自適應控制
中圖分類號:TP273 文獻標志碼:A 文章編號:2095-2945(2017)26-0012-02
引言
近年來,模型參考自適應控制,作為一種重要的自適應控制,它已具有較成熟的分析綜合理論和方法,并在實踐中被越來越廣泛地使用。于此同時,PID因其良好的可靠性和自適應性,也隨之迅速發展。但是,未知特性(如不確定性、隨機性)的外界干擾,對于PID控制的參數變化的影響很大,使其控制效果不佳。這樣,單單用PID控制已遠遠不能滿足要求。隨著人工神經網絡的不斷發展,它能充分應對系統參數較大的情況,能充分展現系統的參數結構,將它與PID控制結合起來,能很好地解決PID控制中的不能,促進兩者的共同發展。本文采用RBF神經網絡進行系統辨識,優點在于其有簡單的結構和很強的適應能力,擁有自我的學習能力。而且運用單神經元作為控制器的PID控制,也考慮了其簡單、易實現性。在通過仿真實踐證明,這種方法在信息的采集、動態特性和在線辨識都有很好的效果。
1 RBF神經網絡辨識
RBF神經網絡是由J.Moody和C.Darken在20世紀80年代提出,它是具有單隱層的三層前饋網絡。它由輸入到輸出的映射是非線性的,而隱含層空間到輸出空間的映射是線性的,這樣能大大加快學習速度并避免局部出現的小問題。
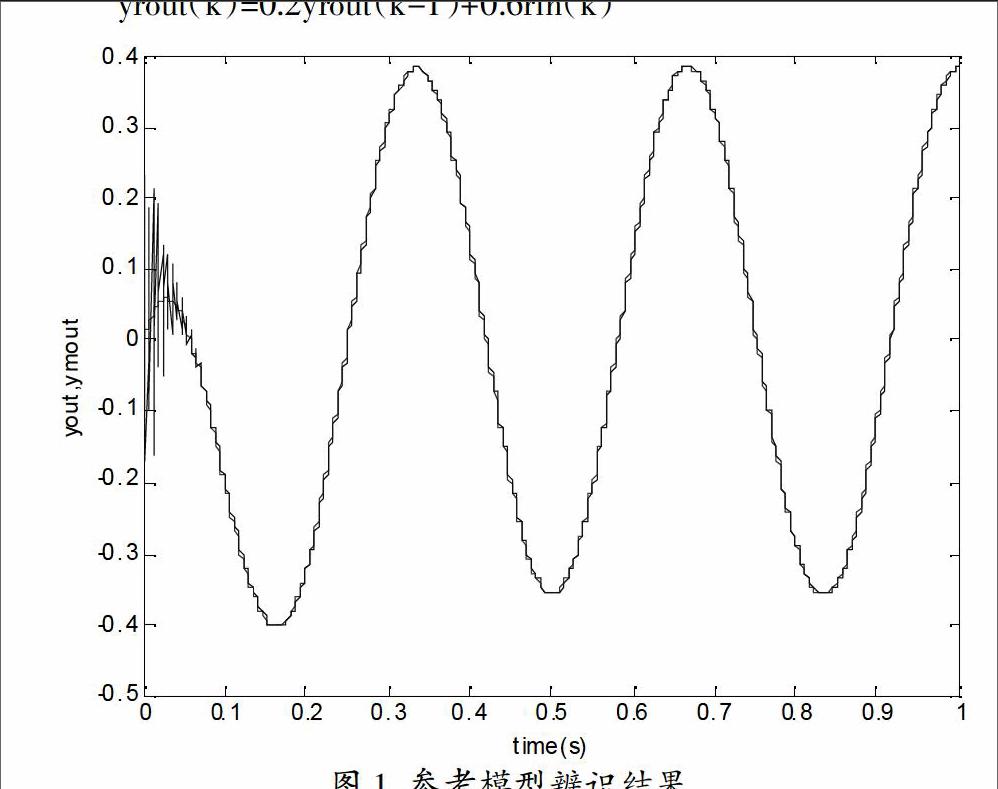
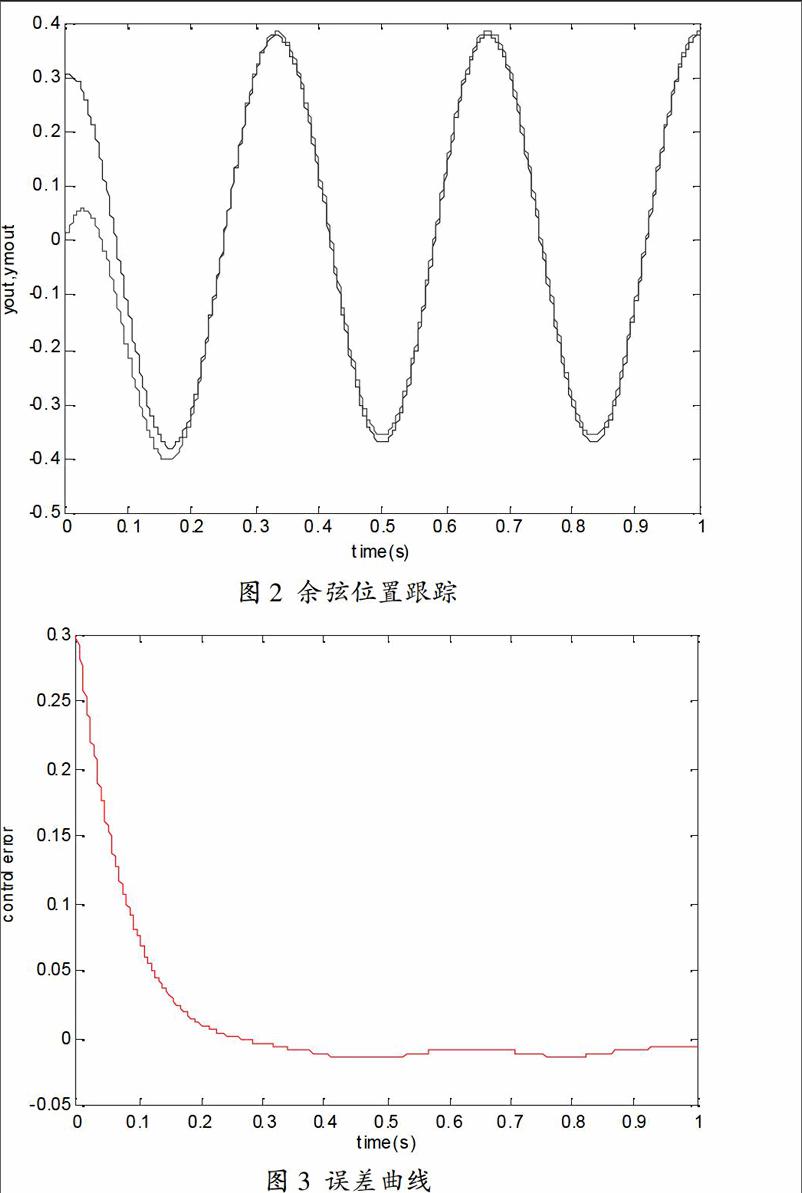
RBF神經網絡輸入層向量記為X(k),該層第i層節點的輸入為xi(k),(1 辨識網絡輸出記為ymout(k),則 ymout(k)=w1(k)h1(k)+…+wn(k)hn(k) (1) 徑向基函數hj(k)為: (2) 其中,Cj(k)為中心矢量,bj(k)為基寬向量。 辨識器的性能指標函數為: 其中,yout(k)為實際輸出。 RBF函數中確定寬度和中心向量參數是系統辨識的關鍵:中心向量通過動態遞推來進行調整;寬度是通過運用最小二乘法(RLS)修改權值計算得到。 2 單神經元PID控制 單神經元作為構成神經網絡的基本單位,具有學習和自適應能力,且結構簡單相應速度快。將它與傳統的PID控制器結合起來,一定程度上解決了傳統PID調節器不易在線實時整定參數,難以對復雜過程和時變系統參數進行有效控制等問題。 單神經元調節器為多輸入單輸出,可通過調整權值得到新的輸出。 其中,輸入量為xci,對應的權值為wci,k為比例系數。 單神經網絡的輸入: 式中,error(k)為誤差;T為時間。 神經網絡的輸出即為控制器的輸出: 單神經元控制器的學習規則采用delta學習規則,主要是調整權重,調整加權系數以達到自適應的效果。二次性能指標函數: E=(yrout(k)-yout(k))2(6) 其中,yrout(k)為模型參考輸出。 辨識網絡會漸漸地與對象的實際輸出一致,即ymout(k)≈y(k)。 最終單神經元權值調整公式為: ?駐wci=-?濁error(k)xci(k)(7) 其中,?濁為學習率,通過RBF神經網絡辨識得到。 3 系統模型和整體結構 系統選取位置伺服控制系統作為被控對象,該系統傳遞函數為: 其中,?茲1(s)、?茲d(s)為輸入端及輸出端電位計(接觸式絕對角傳感器)的偏角,Kp為電位計比例系數,Ka為放大器增益,K0為電樞參數,N為傳動齒輪齒數比,J為系統轉動慣量,B為測速伺服電機參數。 RBF網絡作為辨識器NNI,單神經元PID作為控制器NNC。 4 控制算法 單神經元PID控制器為控制網絡,RBF神經網絡即辨識網絡,對控制系統在線進行辨識,隨時調整參數。這樣,就能獲得更好的控制效果。 其控制過程如下: (1)給出單神經元初始權值、學習速率及RBF網絡的參數。一般,辨識權值wi∈[-1,1],RBF函數中心向量Ci∈[-1,1],寬度bj∈[-1,1]。 (2)采樣得到輸入和反饋rin(k),y(k),這樣就能求出誤差error(k)=rin(k)-y(k),利用公式(4)求出各誤差。 (3)利用公式(5)計算單神經元的輸出,其輸出為PID給出控制量。PID控制器的輸出u(k)發送到被控對象和 RBF網絡就形成實際輸出yout(k)和辨識輸出ymout(k)。 (4)計算RBF中辨識網絡的輸出,由公式(1)求得。 (5)徑向基函數中心向量通過動態遞推來進行調整;寬度是通過運用最小二乘法修改權值計算得到。 (6)模型參考輸出yrout(k)與實際輸出yout(k)的偏差由修正單神經元的權值得到。 (7)k=k+1,進行循環移位并返回步驟(2)。 5 仿真 針對二階傳遞函數進行單神經元 PID模型參考自適應控制,被控對象離散化得到差分方程: y(k)=1.9815y(k-1)-0.9818y(k-2)+0.1656u(k-1)+0.1646u(k-2) 采樣時間T為1ms,當S=1時,輸入指令信號為余弦信號;當S=2時,輸入的參數辨識以及余弦跟蹤結果如圖1、圖2、圖3所示。 參考模型指令信號為: rin(k)=0.5cos(0.006?仔k) yrout(k)=0.2yrout(k-1)+0.6rin(k) 6 結束語 本文采用了RBF神經網絡進行網絡辨識,運用單神經元PID控制器實現自適應控制。仿真運用位置伺服控制系統的傳遞函數作為被控對象,表明了神經網絡有很好的學習功能、較好的辨識精度,以及實現調整系數的目的。另一方面,單神經元構成的PID控制器結構簡單,適應性強,大大地簡化了工作的復雜性,提高精度和實現在線辨識的要求。所以,系統中參數辨識和控制器參數實現連續在線調整,這種方法有助于工程實踐應用。 參考文獻 [1]劉金坤.先進PID控制MATLAB仿真(第2版)[M].北京:電子工業出版社,2004. [2]鄭晉平.基于RBF神經網絡辨識的單神經元PID模型參考自適應控制[J].電子技術與軟件工程,2015(19):18-19. [3]施鈐.基于徑向基神經網絡辨識的單神經元PID控制[J].安徽電子信息職業技術學院學報,2007,6(4):90-92. [4]吳平景.基于神經網絡系統參數辨識的自適應控制方法研究[D].廣東工業大學,2015. [5]張學燕,張建俠.單神經元自適應PID控制器的研究及MATLAB仿真[J].自動化技術與應用,2007(9). [6]何繼愛,黃智武,田亞菲.一種單神經元PID控制器[J].甘肅科學報,2004(12).

