復合材料層合板中單層就位效應分析
吳義韜
摘 要:復合材料多向?qū)雍习逯袉螌恿W性能不同于單向板力學性能,表現(xiàn)出明顯的就位特性。文章采用能量準則法和經(jīng)驗公式法對復合材料層合板中90°層的就位特性進行了評述,基于試驗數(shù)據(jù)對這兩類方法進行了分析。結(jié)果顯示,能量準則法很好預測了薄90°就位層的就位橫向拉伸強度,而對厚90°就位層預測能力弱;由于面內(nèi)剪切損傷機理復雜,兩種方法對就位剪切強度的預測誤差較大。
關(guān)鍵詞:復合材料;層合板;單層;就位效應;分析
中圖分類號:V262 文獻標志碼:A 文章編號:2095-2945(2017)26-0027-02
引言
復合材料單層就位于多向?qū)雍习逯幸蛩幬恢貌煌斐稍搯螌语@露出同一材料不同力學特性的效應,稱為就位效應(in-situ effect)。多向?qū)雍习逯酗@露該效應的單層或含有相同鋪向連續(xù)堆疊的族聚層(clustered plies)稱為就位層。復合材料存在橫向拉伸就位效應和面內(nèi)剪切就位效應這一現(xiàn)象廣泛被學者認同,且就位橫向拉伸強度和就位面內(nèi)剪切強度作為材料的非固有屬性被越來越多的引入以強度為判據(jù)的失效判據(jù)中。
橫向拉伸就位效應研究較多,而面內(nèi)剪切就位效應相對少。復合材料就位效應主要集中在就位層厚度效應和鄰近層約束效應的研究。本文采用能量準則法和經(jīng)驗公式法對復合材料多向?qū)雍习逯?0°層的就位拉伸和就位剪切效應進行了評述,基于試驗數(shù)據(jù)對這兩類分析方法進行了分析。
1 能量準則法
能量準則法認為,斷裂韌度可作為材料破壞的依據(jù),當復合材料就位層中形成新的橫向裂紋所釋放的能量Gc等于材料橫向斷裂韌度Gmc時,新裂紋就會產(chǎn)生。
能量準則法的關(guān)鍵是求解形成新裂紋所釋放的能量Gc,Davila-Camanho[1]基于能量準則法提煉了簡化的就位橫向拉伸強度近似估算公式。對于薄就位層,橫向拉伸強度為:
(1)
式中,YT,is為就位橫向拉伸強度;GIc(L)為沿縱向裂紋擴展斷裂韌度; 。
對于厚就位層,橫向拉伸強度為:
(2)
式中,GIc(T)為沿橫向裂紋擴展斷裂韌度;YT為單向板橫向拉伸強度。
考慮了面內(nèi)剪切非線性,Davila-Camanho[2]引入Hashin-Tsai的剪切非線性表達式,就位剪切強度為:
(3)
對厚就位層, ;
對薄就位層, 。
能量準則法從能量轉(zhuǎn)化和守恒角度研究就位層多重基體開裂,用傳統(tǒng)的斷裂力學處理就位層基體裂紋開裂的問題。所用的模型做了諸多假設(shè),與實際開裂現(xiàn)象不完全吻合。分析模型針對內(nèi)含90°就位層的典型對稱結(jié)構(gòu),因而能量準則法在分析真實層合板結(jié)構(gòu)就位特性時受到了限制。
2 經(jīng)驗公式法
Chang-Lesard[3]提出了一個預測層合板中就位層的就位橫向拉伸強度和就位剪切強度的經(jīng)驗公式模型:
(4)
(5)
式中,參數(shù)A、B、C、D根據(jù)試驗結(jié)果擬合得到。
經(jīng)驗公式模型建立就位橫向拉伸強度和就位剪切強度與就位層厚度以及鄰近層夾角之間的關(guān)系,本質(zhì)是一個經(jīng)驗計算公式,沒有深入就位層基體破壞模式研究。公式中的參數(shù)與材料有關(guān),由試驗數(shù)據(jù)擬合得出。當真實結(jié)構(gòu)中當前分析層與上下鄰近層之間夾角不一致時,經(jīng)驗公式法根據(jù)夾角“取小”原則,來確定該結(jié)構(gòu)形式下的當前分析層的就位強度,這樣簡化處理本身缺乏依據(jù)。
3 對比分析
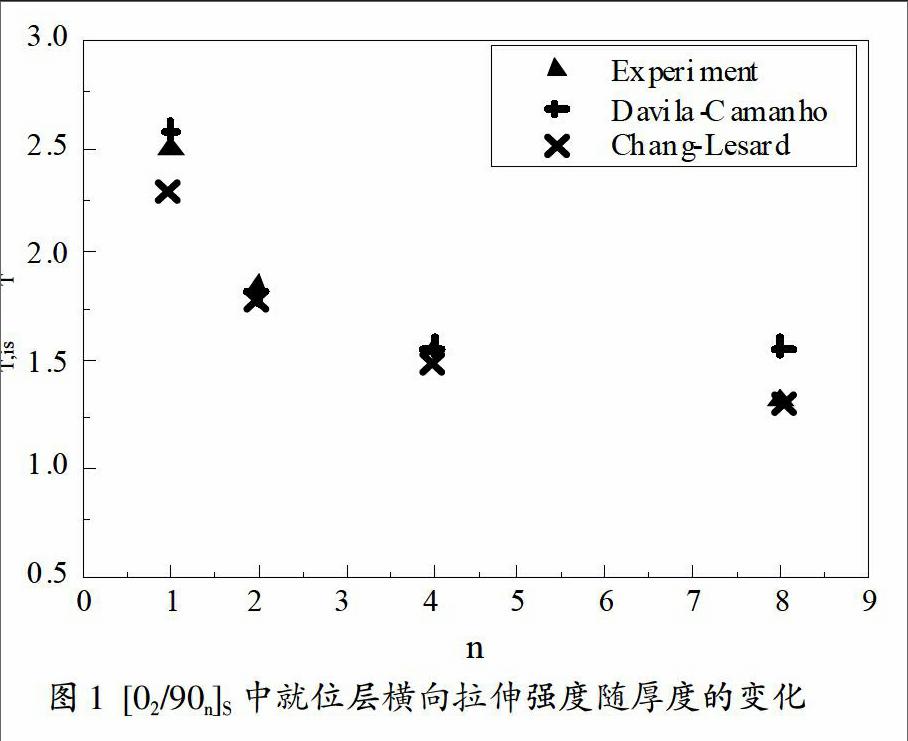
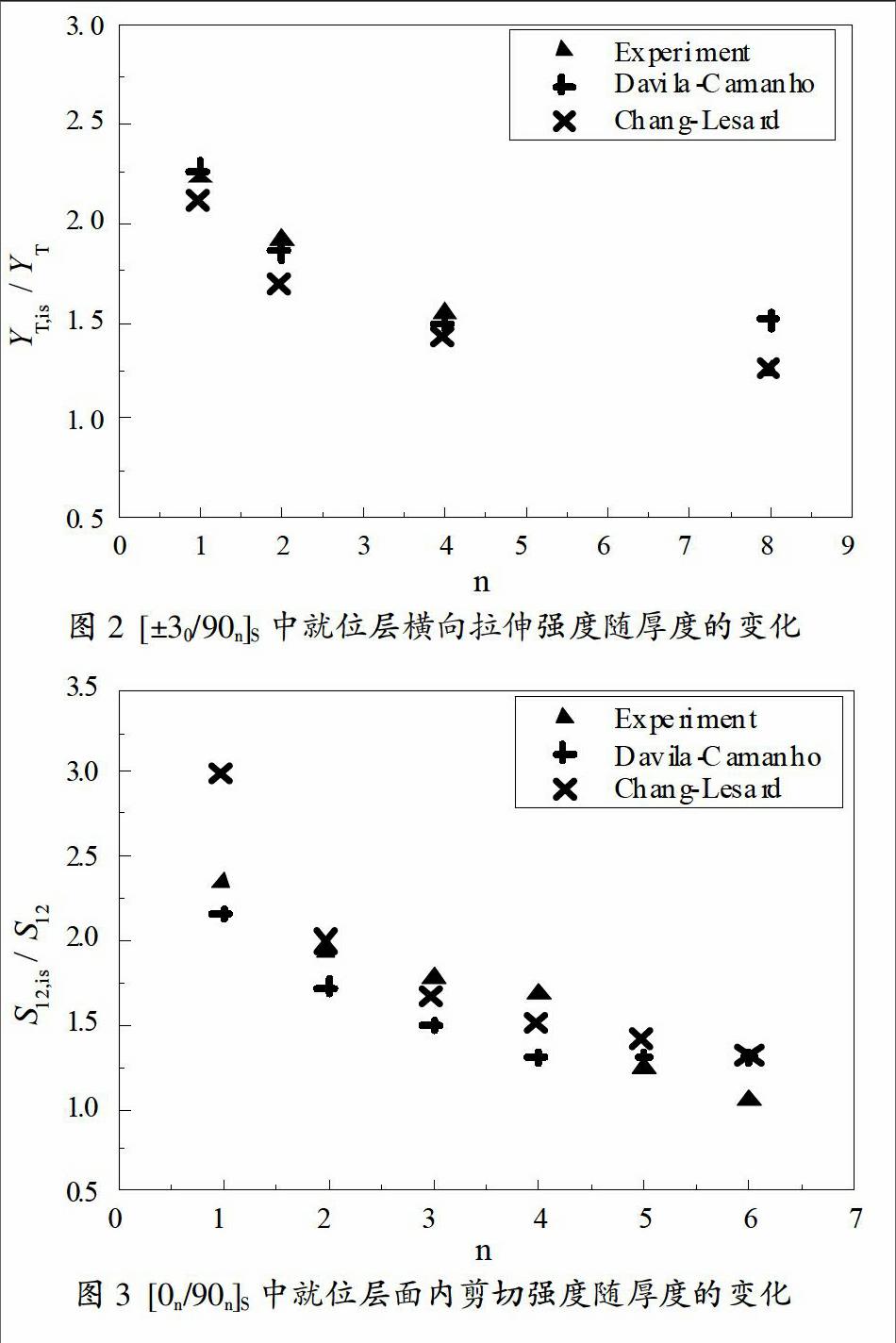
[02/90n]S和[±30/90n]S鋪層形式下,Davila-Camanho模型和Chang-Lesard模型預測的就位橫向拉伸強度與試驗結(jié)果對比見圖1和圖2,圖中橫坐標為90°層層數(shù),縱坐標為正則化的就位強度因子(YT,is/YT)。試驗數(shù)據(jù)來源于文獻[4]。結(jié)果顯示,90°就位厚度較小(n≤4),即鄰層強約束時,兩種模型預測結(jié)果與試驗值吻合都較好,Davila-Camanho模型相對更優(yōu);90°就位層厚度較大時,Chang-Lesard模型預測值與結(jié)果吻合很好,而Davila-Camanho模型與試驗結(jié)果差異較大。
[0n/90n]S鋪層形式下,Davila-Camanho模型和Chang-Lesard模型預測的就位剪切強度與試驗結(jié)果見圖3。試驗數(shù)據(jù)來源于文獻[5]。結(jié)果顯示,鋪層層數(shù)n較小(n=1),即鄰層強約束時,預測結(jié)果與試驗值相差較大,Davila-Camanho模型預測能力相對好些;鋪層層數(shù)n較大時,Chang-Lesard模型和Davila-Camanho模型預測結(jié)果與試驗值吻合得一般。兩種模型預測誤差較大與剪切破壞機理復雜有關(guān),n較小時剪切破壞機理尤為復雜。
4 結(jié)束語
能量準則法能很好預測薄90°就位層的就位橫向拉伸強度,而對厚90°就位層預測能力弱。就位層較厚時,經(jīng)驗公式法預測結(jié)果與試驗值吻合較好。
面內(nèi)剪切伴隨多種損傷模式耦合發(fā)生,導致就位剪切強度預測結(jié)果與試驗值誤差較大。
為了充分發(fā)揮復合材料的就位特性,相同方向連續(xù)堆疊的層數(shù)不宜過多,最好不要超過2層。
參考文獻:
[1]Davila C G, Camanho P P, Rose C A. Failure Criteria for FRP Laminates[J]. Journal of Composite Materials. 2005, 39: 323-345.
[2]Camanho P P, Davila C G, et al. Prediction of in situ strengths and matrix cracking in composites under transverse tension and in-plane shear[J]. Composites Part A: Applied Science and Manufacturing. 2006, 37(2): 165-176.
[3]劉莉.復合材料在汽車制造中的應用[J].科技創(chuàng)新與應用,2012
(28):110.endprint

