扇形覆冰導線舞動特性數值模擬分析

陳友慧，楊繼業，馬 強，鄢 闖，李冬雪

(國網遼寧省電力有限公司經濟技術研究院，遼寧 沈陽 110015)

扇形覆冰導線舞動特性數值模擬分析

陳友慧，楊繼業，馬 強，鄢 闖，李冬雪

(國網遼寧省電力有限公司經濟技術研究院，遼寧 沈陽 110015)

以基于輸電線路檔間舞動為正弦半波的假設，考慮氣動力與導線運動的速度耦合，利用D’Alembert原理建立的扇形覆冰輸電導線三自由度舞動方程，并依據工程實例中的相關參數，使用MATLAB軟件對覆冰導線進行數值模擬分析，研究導線起舞的風速條件下，不同攻角對扇形覆冰導線舞動特性的影響。結果表明，利用水平、垂直及軸向3個方向上的舞動振幅判斷輸電導線舞動臨界條件與實測結果比較接近，符合Nigol舞動機理。

輸電線路；導線舞動；攻角；數值模擬

1 背景概述

隨著人們對電力的需求越來越大，對輸電塔線體系的輸電容量要求也日益增大，輸電線作為電力輸送的主要載體將會跨越更多高海拔及氣象條件極為惡劣的山區與平原地帶。導線覆冰是造成導線舞動的必要條件，半液態的雨點凝集在導線迎風面偏上方，形成導線偏心結冰。由于導線偏心結冰改變了導線的幾何形狀，使導線的一側形成一個翼面[1]。在氣候條件較為特殊的地區，就可能在輸電導線的迎風面結冰，而輸電線結冰截面形狀的不同，使導線的受力情況變得復雜多變，從而使導線在一定的風速和攻角條件下，發生大幅、低頻的自激振動，即發生舞動。

根據大量的氣象觀測資料以及試驗結果可以得知，霜淞和雨淞這兩類覆冰的附著力比較大，而輸電導線所形成的覆冰形狀大多以扇形和新月形為主。在氣溫很低，雨量較小，雨淞細化，風速適中的氣象條件下會使輸電導線形成新月形覆冰；而在氣溫較低，雨量較大，雨淞較粗，風速較大的時候，則會使輸電導線形成扇形覆冰。我國湖北地區形成的導線偏心覆冰厚度一般為15～20 mm，最為嚴重的則會達到38～48 mm。由于覆冰的隨機性和多樣性，以及相關風洞試驗的測量精度和手段有限、存在費用高、試驗周期較長問題，同時由于試驗模型和實際問題等效性等方面的局限性，無法滿足實際工程多樣性需求的獲取。在20世紀80年代以后，隨著流體力學算法的進步，很多輸電導線舞動問題可以通過數值仿真模擬分析來實現。華中科技大學對輸電覆冰導線的空氣動力特性進行了一系列試驗[2-3]。隨著風速的增加舞動趨勢越來越大，導線舞動的持續時間取決于大氣條件的變化和導線覆冰的脫落情況。當風向改變、風速降低或氣溫回升使覆冰融化脫落時，舞動也停止[4]。為了滿足扇形覆冰導線舞動計算與仿真的需要，本文根據空氣動力學、牛頓定律和D’Alembert原理，依據覆冰導線的動力學模型，使用MATLAB軟件對覆冰導線的舞動特性進行數值模擬分析，在起舞風速條件下，對不同攻角及檔距對覆冰導線三相位移平面圖進行數值分析，研究覆冰導線的舞動特性，為覆冰導線制定有效的防舞措施提供相應的理論依據。

2 扇形覆冰導線舞動的振子模型動離散化

輸電導線的覆冰特性與風向、風速、氣溫、導線走向及海拔高度等諸多因素有關，Makkonen[5]根據降水率、氣溫、導線半徑、風速、風攻角以及覆冰所需要的時間建立覆冰模型，得到在氣溫0 ℃左右時導線會產生最大的覆冰荷載；Masoud[6]通過現場實測資料的分析得出，在潮濕條件下輸電導線的結冰率遠遠大于在干燥條件下的結冰率。為此本文根據扇形覆冰的形成條件，在考慮輸電導線自重及其覆冰重量條件下，假設覆冰內邊緣圓心角140°，外邊緣圓心角120°。根據三自由度基本動力學方程，在考慮覆冰質量以及輸電導線自重條件下，由風荷載對導線產生空氣動力的氣動升力、氣動阻力以及扭轉動力，導線的不平衡張力和由偏心覆冰質量所引起的慣力矩、重力矩以及空氣動力矩等，對覆冰導線的振子模型進行無量綱化，依據微分變換法及MATLAB程序將導線的舞動方程進行離散，求出舞動方程的數值解。

3 扇形覆冰導線在起舞條件下攻角對舞動的影響

本文根據編寫的MATLAB程序得到覆冰導線在起舞風速條件下發生舞動時的時程曲線圖。根據湖北大跨越輸電線路的工程數據，在偏心覆冰條件下，當風速達到10 m/s時，導線就會發生舞動。故在數值模擬中，分別模擬攻角α為105°、125°、145°時，覆冰導線中心點的三相位移平面圖軌跡，如圖1所示。

(a)α=105°

(b)α=125°

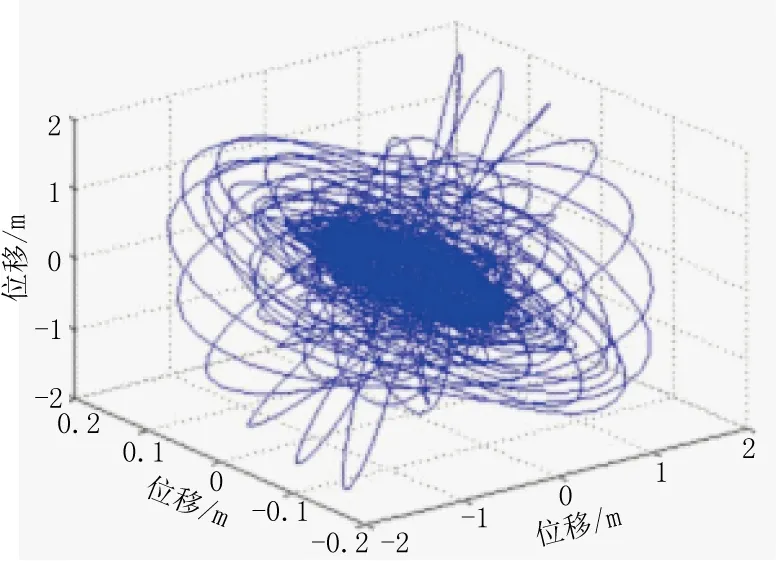
(c)α=145°圖1 3種攻角條件下覆冰導線三相位移平面圖

根據分析結果可知，輸電導線在偏心覆冰條件下發生舞動后，隨著風速越來越大，導線的振動會越來越弱，3個方向上的位移隨著時間的增加而增大；當達到某一個最大值時，隨著時間的增加而減小，最后趨近于某一個最小值，在其附近作小幅振動，這符合自激振動的原理。無論風速多大，位移最后都會趨于某一個值，不會無限增加，主要是因為導線的振動是非線性運動，即使失穩，也會在某一個極限值時穩定下來，只有對線性系統來說，系統一旦失穩，振幅會一直增加。因此導線的攻角越大，振動就會越來越激烈，此時在理論上，倘若繼續增大攻角，就會使導線發生失速顫振。為此，根據數值模擬分析可以得到，當α達到145°時，覆冰導線開始舞動，與風洞試驗的結果相符合。

4 覆冰導線舞動的防舞措施

根據目前所了解到的舞動機理和現象，大多采用現場觀測與試驗研究相結合以及由定性向定量逐步深化的方法進行探究，目前已經取得了一些比較顯著的成績，也摸索到了一些比較有效的防舞措施以及計算方法，但是對于扇形覆冰導線防舞措施的制定還有待于進一步研究與確定。

湖北大跨越的實測冰型為扇形，針對導線的初始攻角進行了理論推導以及數值仿真模擬，根據數值模擬結果，對防舞工作的思路及發展進行拓展。風向與導線的成角大小會對覆冰導線的冰截面形狀產生相應的影響，當地的雨雪情況同樣會影響輸電導線的舞動，所以在技術經濟指標允許的情況下，盡可能避開強風舞動地區，在線路走向上則應該盡可能減小冬季風向與線路走向的夾角，從改變與調整輸電導線的系統參數出發，更廣泛地應用覆冰在線監測系統進行導線的運行維護工作。

5 結束語

綜上所述，根據實測冰型對湖北大跨越輸電線路進行數值模擬，通過改變導線的風攻角，對導線的舞動情況進行分析，得出在理論上得到的起舞條件與實測的舞動條件更為接近，使用這種動力學模型對覆冰導線的舞動進行數值分析是可行的，為此還可以從導線直徑等方面對覆冰導線進行理論研究。

[1] 郎振國，劉 良，徐寶臣.通遼地區輸電線路發生覆冰舞動原因及對策[J].東北電力技術,2006,27 (11):48-52.

[2] 李萬平，楊新詳，張立志.覆冰導線群氣動力特性分析[J].空氣動力學報，1995,13(14):427-428.

[3] 李萬平，黃 河，何 锃.特大覆冰導線氣動特性測試[J].華中科技大學學報,2001,29(8):84-86.

[4] 張忠瑞，王 飛，張 巍.遼寧電網輸電線路舞動的氣象影響分析[J].東北電力技術,2012,33(4): 26-31.

[5] Makkonen L. Modeling power line icing in freezing precipitation[C].7th International Workshop on Atmospheric Icing of Structures. Montreal,1996.

[6] Masoud F,Konstantin S. Statistical Analysis of Field Data for Precipitation lcing Accretion on Overhead Power Lines[J]. IEEE Transactions On Power Delivery,2005,20(2):1 080-1 087.

Numerical Analysis of Galloping Character of Fan-Shaped Ice Cover Conductor

CHEN Youhui, YANG Jiye, MA Qiang, YAN Chuang, LI Dongxue

(State Grid Liaoning Electric Power Company Limited Economic Research Institute, Shenyang，Liaoning 110015, China)

The hypothesis of half sine wave of cable galloping in span is adopted. For the problem of fan-shaped ice cover conductor galloping, this paper presents a flabelliform cable galloping model of three degree-of-freedom based on D’Alembert Principle which considers the velocity coupling between air force and the cable torsional vibration. According to the relevant parameters in the project example, it uses the software Matlab for numerical simulation. To explore the flabelliform cable galloping characteristic of the wire on the condition of the wind speed of the wire dancing in different of the angle of attack.Judging the divergence critical condition of power transmission line used the dancing amplitude in horizontal, vertical and axial directions.It meets the galloping mechanism of Nigol. It’s proved this theory is feasible.

transmission line; galloping conductor; the angle of attack; numerical simulation

TM751

A

1004-7913(2017)08-0044-03

陳友慧(1987)，女，碩士，工程師，主要從事輸電線路設計工作。

2017-03-01)