球形機器人的仿真與實驗測試分析
楊 偉,李 健,肖起陽,黃新敬,曾周末
(天津大學 精密儀器與光電子工程學院,天津 300073)
球形機器人的仿真與實驗測試分析
楊 偉,李 健,肖起陽,黃新敬,曾周末
(天津大學 精密儀器與光電子工程學院,天津 300073)
針對雙擺驅動結構的動力學模型過于復雜的問題,提出一種以絲杠螺母調節轉向、雙擺驅動滾動的球形機器人結構。首先,對其機械結構做了分析與說明;其次,應用動力學分析爬坡性能,通過牛頓-歐拉法建立轉向動力學模型,利用拉格朗日方程建立彈跳動力學模型;最后,圍繞爬坡、彈跳與轉向分別展開仿真與實驗。仿真和實驗的結果驗證了機械結構的可行性與動力學分析的準確性,動力學模型有效簡化。
球形機器人;動力學模型;牛頓-歐拉法;拉格朗日方程
0 引言
球形機器人是一種新穎、靈活且環境適應能力強的移動機器人,在軍事、工業生產、儀器儀表以及辦公室巡邏等領域均具有廣闊的應用前景[1,2]。研究表明內驅單元是球形機器人的核心組成部分,決定了球形機器人的性能[3]。近十余年來,國內外研究機構已相繼研制出多種不同結構特點的球形機器人。按內驅單元的結構特點,較具代表性的內驅單元有滾輪驅動[4]、輻式配重驅動[5]、單擺驅動[6]和雙擺驅動[7]。既往研究雖取得了一定成果,然而在爬坡、彈跳、轉向和可控性等方面存在諸多性能缺陷,制約了球形機器人的發展與應用。為此,開展球形機器人內驅單元結構的設計研究具有重要的意義。
內驅單元通過改變球形機器人的平衡位置,以驅動系統運動[3]。在Bouguechal等人[4]的滾輪內驅單元中,用電機帶動滾輪沿球殼內壁滾動以改變系統質心位置,滾輪與球殼內壁間易打滑,爬坡能力低,不具備彈跳功能。在Mojabi等人[5]的輻式配重內驅單元中,用電機帶動配重塊沿呈輻射狀分布的金屬桿移動以改變系統的質心位置,多個配重塊的位置控制過于繁雜,爬坡、轉向性能低下,不具備彈跳功能。在孫漢旭等人[6]的單擺內驅單元中,用電機帶動擺錘轉動以改變系統的質心位置,爬坡能力強,但無法轉向與彈跳。為改善球形機器人在爬坡、彈跳和轉向方面存在的性能缺陷,Mahboubi等人[7]提出一種雙擺內驅單元的球形機器人,較其它類型的球形機器人,雙擺驅動的球形機器人爬坡、彈跳和轉向性能均得到明顯改善。然而,由于滾動與轉向間存在復雜的驅動耦合關系,建模過程繁瑣,動力學模型復雜,難以實現有效控制。為此,本文在雙擺式內驅單元結構中,添加絲杠螺母作為轉向調節機構,從而分離滾動與轉向間的驅動耦合關系,以有效簡化動力學模型,提高系統可控性。首先,對機械機構以及內驅單元的驅動原理做分析與介紹;其次,分別建立爬坡、轉向和彈跳的動力學模型;最后,加工制作1套實驗樣機,并進行相應的實驗和仿真驗證,得出仿真和實驗結果。
1 機械結構
如圖1所示,本文提出的球形機器人由三部分構成:球形殼體、搭載平臺和內驅單元。內驅單元由3臺步進電機、2個擺錘和1套絲杠螺母裝置構成,3臺步進電機的中軸線與絲杠螺母的中軸線共線,構成機器人的長軸。殼體兩側的步進電機用以驅動擺錘繞長軸旋轉,構成雙擺結構;與絲杠鉚接的步進電機用于驅動螺母沿絲杠移動,使系統質心位置沿長軸移動,從而調整機器人長軸與水平面間的夾角,以輔助調節系統轉向。3塊沿圓周分布的平板固定于殼體內部,以安裝電路板。球形殼體向外凸出的鰭狀結構,一方面,擴大殼體內部空間;另一方面,在轉向過程中,限制長軸與水平面間的最大傾斜角度,提高轉向運動穩定性。
2 動力學分析
2.1 爬坡能力
設球形機器人沿坡度為θ的斜面以無滑滾動的方式作爬坡運動。擺錘質量為m(kg),質心與殼體幾何中心通過長度為l(m)的輕桿固連;除擺錘外的剩余部分近似等效為質量為M(kg),半徑為R(m)的均質薄壁球殼;當前時刻,擺錘的偏轉角為φ(rad),如圖2所示。
根據文獻[8],由動力學分析可得,球形機器人的爬坡條件為:
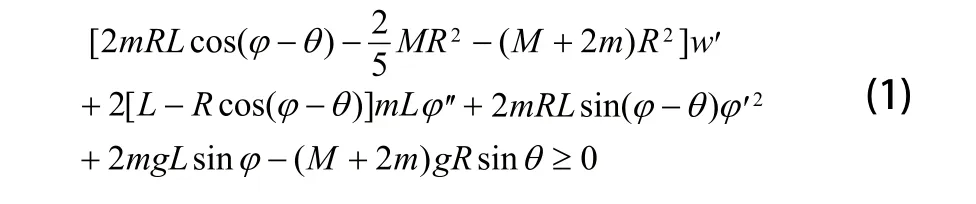
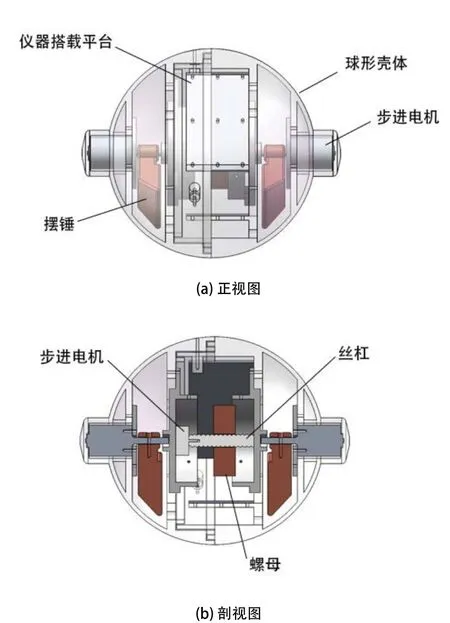
圖1 三維機械結構
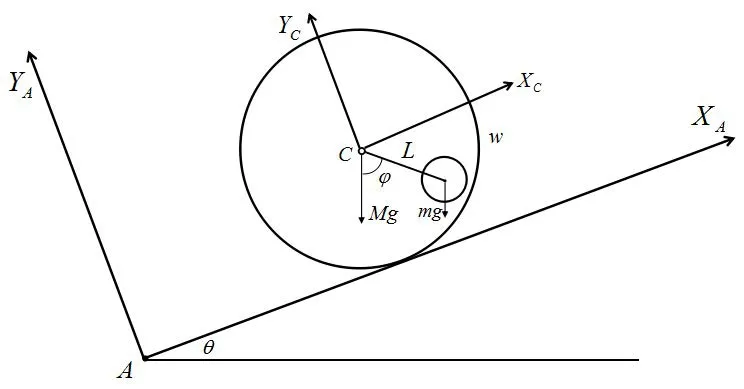
圖2 球形機器人爬坡示意圖
2.2 轉向運動
如圖4所示,球形機器人在水平面上以無滑滾動的方式作轉向運動。設球形機器人長軸與水平面間夾角為β(rad),殼體半徑為R,運動過程中所受摩擦力為f(N);螺母質量為m0(kg)質心為O,與殼體幾何中心間的距離為d(m);兩側擺錘質量均為m,質心分別為P和Q,質心間矩離為2l,擺臂長度均為L;設轉彎半徑為r,如圖3所示。
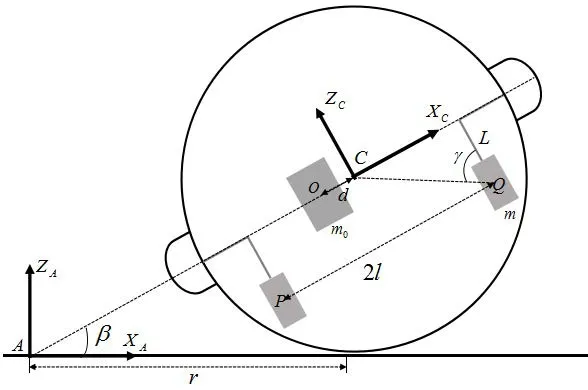
圖3 轉向運動示意圖
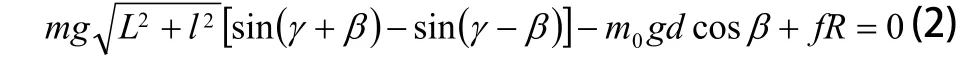
2.3 彈跳運動
設球形機器人由水平面彈跳躍起,躍起高度為h(m);擺錘質量為m(kg),除擺錘外的剩余部分近似等效為質量為M(kg)的均質薄壁球殼;當前時刻,兩側擺錘與短軸間夾角均為α(rad),轉速大小相等,方向相反,擺臂長度均為L,如圖4所示。
由第二類拉格朗日方程[10],可求得球形機器人彈跳運動的動力學模型為:應用牛頓-歐拉法[7,9],建立球形機器人轉向運動的動力學模型為:
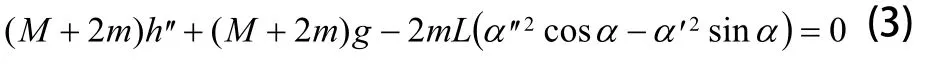
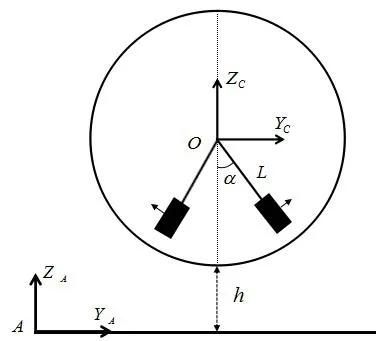
圖4 彈跳運動示意圖
3 實驗與仿真
3.1 爬坡性能測試實驗
設置斜面坡度為5°、10°、15°、20°和25°,對球形機器人實驗樣機的爬坡性能進行實驗測試,實驗結果如表1所示。
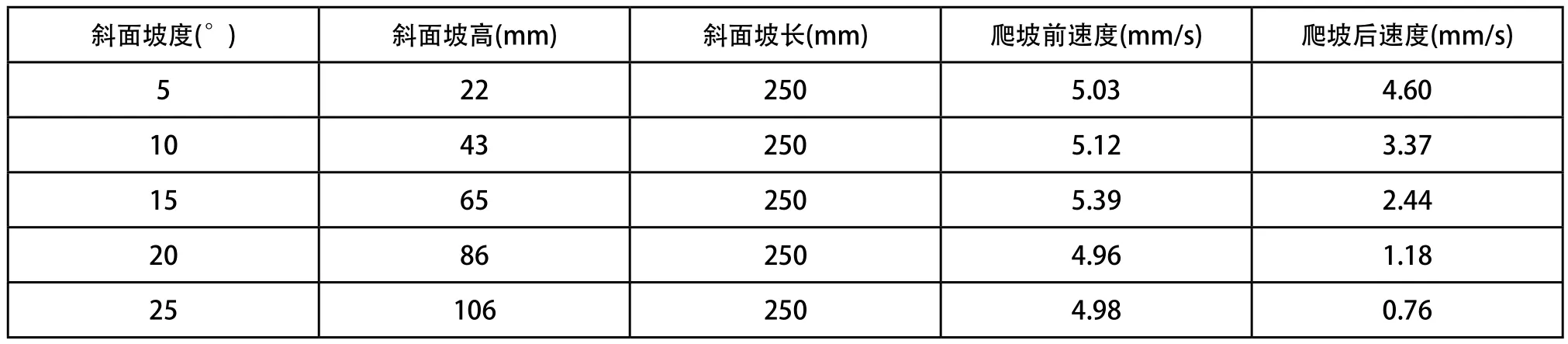
表1 爬坡測試實驗結果
由爬坡測試實驗數據可得,球形機器人在以5mm/s速度緩慢運動過程中,可爬越傾斜角度為25°的斜坡障礙物,由此可見,球形機器人的爬坡越障能力較強。
3.2 轉向性能仿真與實驗
根據文獻[11],為驗證動力學方程式(2),應用MATLAB求解方程解,計算球形機器人的最小轉向軌跡,應用ADAMS機械系統仿真軟件仿真球形機器人的最小轉向軌跡,利用球形機器人實驗樣機對最小轉向軌跡做實驗測試。在MATLAB計算、ADAMS仿真過程中,所用到的主要相關參數如表2中所列。在ADAMS仿真過程中,為保證仿真結果較為準確,將在Solidworks軟件中設計的球形機器人三維機械結構導入,以建立完整的虛擬物理模型(圖5)[12]。轉向實驗過程中,使用固定于球形機器人正上方的高速像機對轉向過程連續拍攝,根據獲取的圖像數據幀(圖6),繪制出實驗過程中球形機器人的最小轉向軌跡。
圖7為球形機器人最小轉向軌跡的理論計算結果、ADAMS仿真結果以及實驗測試結果。MATLAB求解出的最小轉向軌跡理論值為圓周軌跡,半徑約為130mm。ADAMS仿真得出的最小轉向軌跡、實驗測試得出的最小轉向軌跡,均與理論軌跡較為接近,因此,可驗證動力學方程(2)式準確可靠。
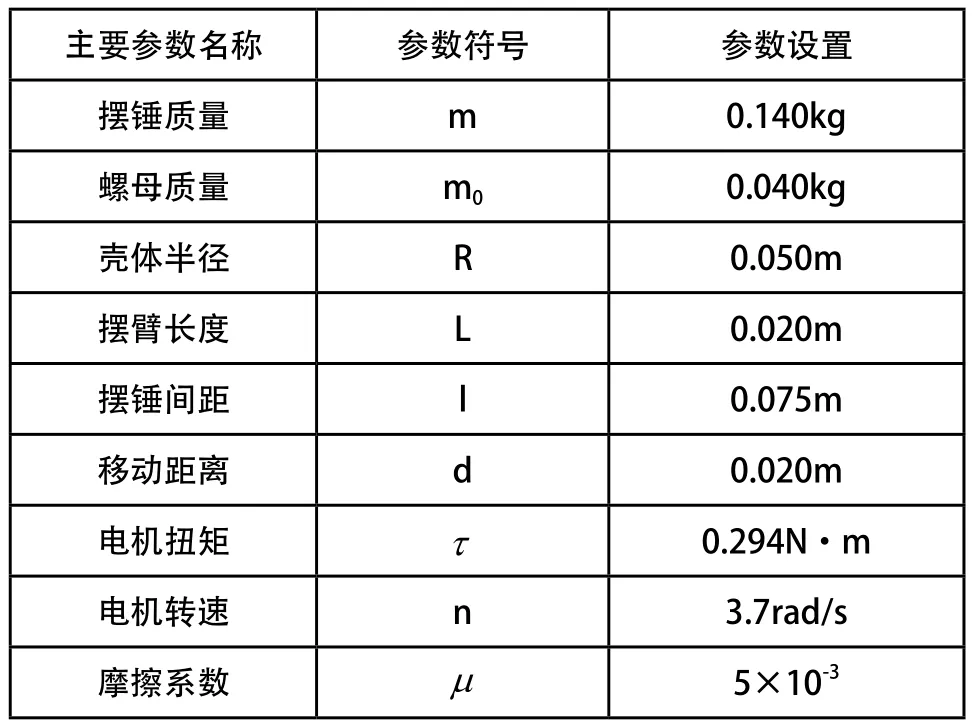
表2 主要相關參數
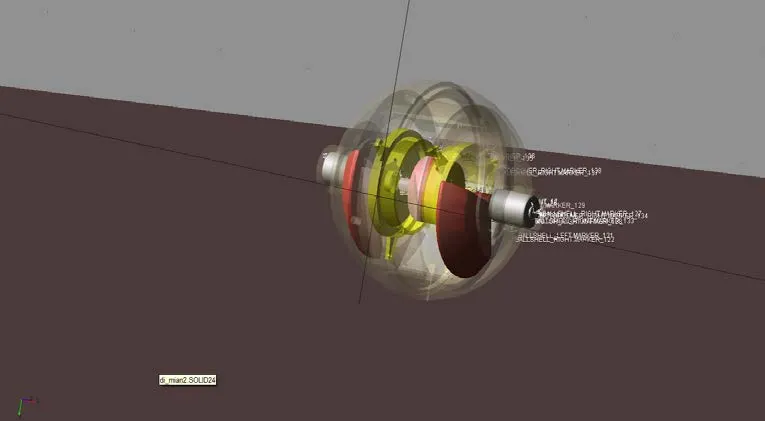
圖5 在ADAMS中建立的虛擬物理模型

圖6 轉向測試實驗圖
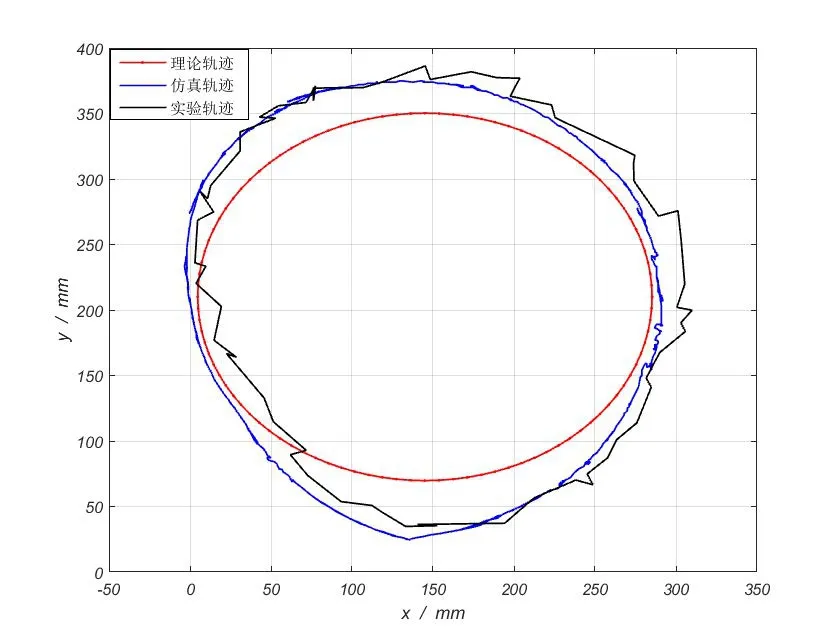
圖7 最小轉向軌跡圖
3.3 彈跳性能仿真與實驗
[12],為驗證動力學方程(3)式,應用MATLAB求解方程解,計算球形機器人的彈跳高度理論值,應用ADAMS機械系統仿真軟件仿真球形機器人的彈跳高度,利用球形機器人實驗樣機進行彈跳實驗測試。已知球形機器人的總質量為0.462kg,其余主要相關參數參考表2。轉向實驗過程中,使用固定于球形機器人正前方的高速像機對彈跳過程連續拍攝,重復實驗5次,根據獲取的圖像數據幀(圖8),得出每次實驗過程中球形機器人的彈跳高度值,彈跳實驗結果如表3所示。
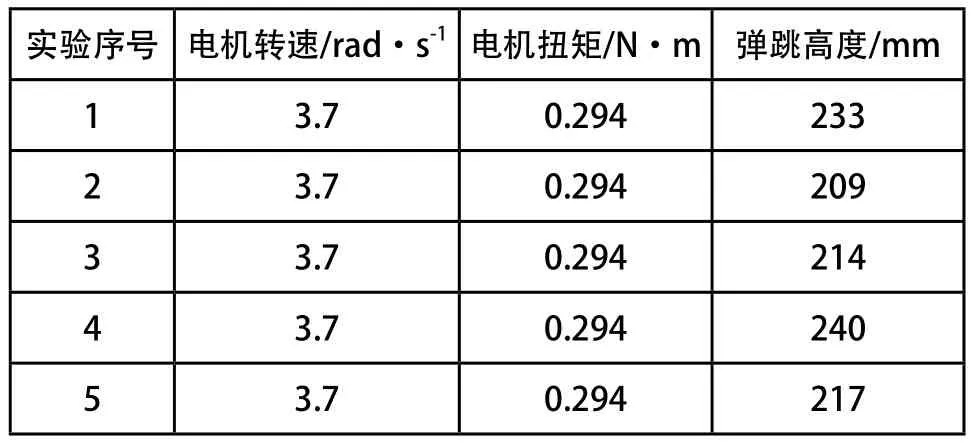
表3 彈跳實驗結果

圖8 彈跳性能實驗測試圖
圖9為球形機器人彈跳高度的理論計算結果以及ADAMS仿真結果,MATLAB求解出彈跳高度理論值約為275mm,ADAMS得出的彈跳高度仿真值約240mm。彈跳實驗重復進行5次,實驗樣機的彈跳高度最小值為209mm,最大值為240mm,平均值為223mm。較理論值,彈跳高度的仿真值降低12.7%,實驗平均值降低18.9%。由此可見,彈跳高度的理論值、仿真值和實驗值間的誤差波動較小,動力學方程(3)式較為準確可靠,球形機器人可彈跳越過高度約200mm的障礙阻擋,具有較強的彈跳越障能力。

圖9 彈跳運動的理論與仿真曲線
4 結論
本文對雙擺驅動結構做改進,為分離滾動和轉向間的驅動耦合關系,加入絲杠螺母作為轉向調節機構。動力學分析表明,對比文獻[7]提出的雙擺式驅動的球形機器人,本文提出的球形機器人結構,動力學模型簡化,可控性提高。爬坡性能測試實驗結果表明,球形機器人的爬坡越障能力較強,緩速滾動過程中,可越過傾斜角度低于25°的傾斜障礙物;轉向仿真與實驗結果表明,轉向性能穩定、良好,最小轉向半徑為130mm,運動過程中規避障礙物的能力較強;彈跳仿真與實驗結果表明,球形機器人可彈跳越過高度約為200mm的阻隔障礙物。因此,本文提出的球形機器人結構具有可行性,爬坡越障、轉向規避障礙以及彈跳越障的能力較強,動力學模型有效簡化,可控性提高,可應用于在復雜地形環境中行走,以完成相關的測量或探索任務等,這為進一步開展球形機器人智能導航控制的研究工作奠定了基礎。
參考文獻:
[1] 趙勃,孫立寧,李滿天.球形機器人研究綜述[J].機械與電子,2010,2010(9):63-68.
[2] 孫漢旭.新型變結構球形機器人運動分析[J].機械工程學報,2013,49(19):40-47.
[3] 鄧宗全,岳明,禹鑫燚,方海濤. 球形運動器動力學分析及控制系統設計[J].機器人,2006,28(6):565-570.
[4] Nour Eddine Bouguechal. Positioning errors consideration for indoor mobile robot design[J].Industrial Robot,2003,30(2):170-176.
[5] Mojabi P. Introducing August: a novel strategy for an omnidirectional spherical rolling robot[C]//Robotics and Automation, 2002. Proceedings. ICRA'02. IEEE International Conference on. IEEE, 2002, 4: 3527-3533.
[6] 蘭曉娟,孫漢旭,賈慶軒.水下球形機器人BYSQ-2的原理與動力學分析[J].北京郵電大學學報,2010,33(3):20-23.
[7] Saber Mahboubi. Design and implementation of a novel spherical mobile robot[J].Journal of Intelligent and Robotic Systems,2013,71(1):43-64.
[8] 王亮清,孫漢旭,賈慶軒.球形機器人的爬坡與彈跳能力[J].北京郵電大學學報,2007,29(2):11-14.
[9] Chen M, Sun W, Gao Y, et al. Development of a holonomic mobile spherical robot with 3D center of gravity shifting actuators[C]//Robotics and Biomimetics (ROBIO), 2016 IEEE International Conference on.IEEE,2016:438-442.
[10] 劉隆,謝偉平.含多余廣義坐標的拉格朗日方程及實例應用[J].力學與實踐,2013,35(3):87-89.
[11] 方琛瑋,莊未,劉曉平,孫漢旭.基于ADAMS的球形機器人的運動學分析[J].機械工程與自動化,2009,(1):118-120.
[12] Zhao W, Sun H X, Jia Q X, et al. Mechanical Analysis of the Jumping Motion of a Spherical Robot[C]//Advanced Materials Research. Trans Tech Publications, 2012, 591: 1457-1460.
The simulation and experimental analysis of a spherical robot
YANG Wei, LI Jian, XIAO Qi-yang, HUANG Xin-jing, ZENG Zhou-mo
TP242
:A
:1009-0134(2017)08-0029-04
2017-06-10
國家自然科學基金資助項目(61374219,51604192)作者簡介:楊偉(19 -),

