分層抽樣在電梯檢驗報告抽查中的應用

黃鵬輝 高 勇

(陜西省特種設備質量安全監督檢測中心 西安 710048)

分層抽樣在電梯檢驗報告抽查中的應用

黃鵬輝 高 勇

(陜西省特種設備質量安全監督檢測中心 西安 710048)

目前電梯的檢驗質量受到了社會的廣泛關注，檢驗報告抽查是對電梯檢驗質量進行控制的重要環節。為解決檢驗報告抽查的科學性和精確性，本文嘗試將統計學上的分層抽樣理論引入電梯檢驗報告抽查中，本文論述了分層抽樣的基本理論及其用于電梯檢驗報告抽查的可行性，介紹了分層抽樣應用于電梯檢驗報告抽查的實施步驟，并進行了實例計算。

分層抽樣 電梯檢驗報告 抽查

近年來隨著社會經濟的發展,我國電梯的數量急劇增加,隨之帶來的安全問題不容忽視。電梯數量的激增和與之相關的安全事故的頻發,使整個社會對電梯的檢驗質量關注度也越來越高。電梯檢驗質量的控制有多種手段,檢驗報告的質量是檢驗質量的重要組成部分[1-2],所以檢驗報告抽查是質量控制的重要一環,通過報告抽查,可以發現檢驗中存在的一些共性問題,進而采取有針對性的措施,以達到提高檢驗質量的目的。目前檢驗報告的抽查多停留在以經驗為主的階段,沒有采用科學的方法進行規范,往往達不到預期的效果。分層抽樣理論由于其科學性和適用性已經在漁業生產統計、森林資產核查,以及實驗室廢液統計等各領域得到廣泛應用[3-5]。本文嘗試以統計學上的分層抽樣理論來解決電梯檢驗報告的抽查問題,以提高抽查的科學性和精確性,并給出了具體的實例計算。

1 分層抽樣理論

抽樣方法是一種綜合了統計技術和管理方法的質控手段,抽樣方法包括簡單隨機抽樣、分層抽樣、整群抽樣,多階段抽樣等多種抽樣方法。在進行抽樣估計時,總體方差是影響估計精度的重要因素,總體方差越大,估計的精度越差;反之,估計的精度越高。總體的方差是客觀存在的且無法改變,但如果能按照某種規則對總體單元進行分類,在子總體內單元之間比較相似,每一個子總體的方差較小,這樣只需在子總體中抽取少量樣本單元,就能很好地代表子總體的特征,從而提高對整個總體估計的精度,這就是分層抽樣技術。分層抽樣要求層內差異較小,層間差異較大。

分層抽樣[6-7]的定義如下所述:在抽樣之前,將總體的N個單元劃分為L個互不交叉、互不重疊的子總體,每個子總體稱為層,它們的大小分別為N1,N2,…,NL,這L個層合起來就是整體總體。然后,對每個層分別獨立地進行抽樣,這種抽樣就是分層抽樣,所得到的樣本稱為分層抽樣。若每層中的抽樣都是簡單隨機抽樣,那么這種分層抽樣就稱作分層隨機抽樣。

對于分層抽樣,在對總體進行推算時,估計量的方差不僅與各層的方差有關,還與各層所分配的樣本量有關。分層抽樣確定各層樣本容量的方法通常有比例分配、最優分配,奈曼分配等三種方式,其中比例分配是實際工作中最為常用的方法。按照比例分配的分層隨機樣本,估計量的形式特別簡單,并且為自加權的樣本。比例分配法分配各層樣本量時,給各層分配的樣本量nh占各層所有單元數Nh的比例是相同的,均等于總樣本量n占總體N的比重。此時,各層應分配的樣本量為(Wh為各層的層權)。

2 利用分層抽樣的可行性

在一般的檢驗機構中,通常都會按照檢驗區域劃分成不同的檢驗部室,不同部室之間的電梯檢驗數量是各不相同的。并且按照TSG T7001—2009《電梯監督檢驗和定期檢驗規則——曳引與強制驅動電梯》的要求,電梯的檢驗至少需要2名有資質的人員,因此一般部室內又會將人員兩兩分組,每組人員由于技術能力和工作經驗的不同,其檢驗的電梯數量也不盡相同,也即一定時期內不同檢驗組出具的檢驗報告數量是各不相同的。若簡單地對每組抽取同樣的報告數量,則對于報告數量較多的檢驗組不能合理地反映其真實狀況,若是一味增加報告的抽查數量,雖然可以提高抽查的精確性,但是質量管理成本卻會急劇增加;另一方面,當每組按照同一百分比抽取報告時,對于不同的檢驗組抽查報告得到的報告無缺陷率,其估計的準確程度也沒有一致性。也就是說,用這種抽查方法得到的無缺陷率衡量不同檢驗組的報告質量,其寬嚴程度也是不相同的:對于報告量較大的檢驗組嚴格,對于報告量較少的檢驗組則顯得寬松。因此就有必要采取科學的統計方法對檢驗報告進行抽查,以期以合理的報告抽查數量較為真實地反映檢驗質量。

實際工作中,同一個檢驗組所出電梯報告的編制人員、審核人員、批準人員是相同;組與組之間的編制、審核和批準人員是不相同的。若以檢驗組來分層,則層內的各單元是比較相似的,由于檢驗人員技術水平,責任心等的不同,層與層之間則差異較大。因此,電梯檢驗報告的抽查宜利用分層隨機抽樣技術。

3 分層抽樣的實施步驟[4,8]

3.1 確定分層方案

以不同的檢驗組為分層因子進行分層,層內方差較小,層間方差較大。可在不增加樣本單元數的條件下,提高估計精度和抽樣效果。在同一檢驗組所出報告中,無缺陷率的概率是相同的,可采用簡單隨機抽樣。

3.2 計算各層的權重

第h層的權重為:

式中:

Wh——第h層的權重(h=1, 2, …, L);

Nh——第h層的報告數量;

N——總體報告數量。

3.3 總樣本量的確定

本文采用比例分配來確定樣本量在各層的分配,這里的比例分配是指按照各層單元數占總單元數的比例,也即按各層的層權進行分配。按比例分配的分層隨機樣本,其估計量的形式比較簡單,并且此類樣本為自加權的樣本。按比例分配時,分層抽樣的總樣本量為:

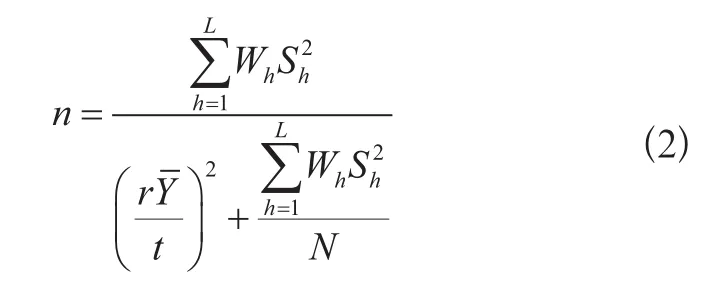
式中:

r——相對誤差限;

t——標準正態分布的雙側α分位數;

Y——總體均值。

式中:r和t是根據抽樣精度預先確定的,Wh和 N為已知數,和是未知數,應根據歷史數據或預抽樣所得數據進行估計。

按照比例分配,各層樣本量為

3.5 估計量的計算

對于電梯等特種設備的檢驗報告抽查,檢驗機構一般會以“無缺陷率”等指標來衡量。無缺陷率也就是無缺陷報告數量占報告總量的百分比,即對總體比例進行估計。

定義

4 實例應用

已知:某單位檢驗電梯共有29組,全年檢驗電梯26900臺,即N=26900。在95%置信度下,相對誤差不超過5%(r=0.05)進行抽樣分析。按照檢驗組分層,共29層,層樣本量的分配采用比例分配。

則總樣本量為:

按照預抽樣所得數據計算相應參數,見表1。

即總樣本量為395份。

表1 參數計算

4.2 各層樣本量分配及抽樣

4.3 總體均值(無缺陷率)的估計

對各層抽取到的報告進行審核,得到每個檢驗組的報告無缺陷率Ph,則總體的報告無缺陷率為:

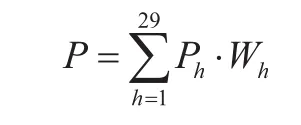
5 結束語

采用比例分配樣本量的分層隨機抽樣方法可應用于電梯檢驗報告的抽查中,相比于傳統的憑經驗抽查方法,更為合理和科學,能提高對總體估計的精度。

[1] 王洪亮，陳莉，馬霞，等．特種設備檢驗質量管理方法的應用[J]．中國特種設備安全，2008，24(12)：9-12．

[2] 楊念慈，蕭艷彤．強化特種設備檢驗質量管理[J]．北京勞動保障職業學院學報，2007，1(4)：47-48．

[3] 甘喜萍，盧伙勝，馮波，等．分層抽樣法應用于漁業生產統計的研究[J]．安徽農業科學，2008，36(20)：8401-8402．

[4] 葛曉麗．分層抽樣理論在森林資源資產核查中的應用研究[J]．農業勘查設計，2014，(1)：4-6．

[5] 修宗明，樊鴻康，金朝暉，等．分層抽樣法在實驗室廢液量統計中的應用[J]．安全與環境學報，2005，5(6)：51-53．

[6] 金勇進．抽樣：理論與應用．高等教育出版社[M]．北京：高等教育出版社，2010．

[7] 齊二石，裴小兵，于延超．產品質量檢驗的分層抽樣法研究[J]．工業工程，2004，7(4)：54-56．

[8] 王寶來，翁澤宇，祝曉青，等．分層抽樣理論在電動釘槍耐久性試驗中的應用[J]．輕工機械，2007，25(5)：99-102．

Application of Stratifed Sampling Method in the Sample Survey of Elevator Inspection Reports

Huang Penghui GaoYong
(Shaanxi Special Equipment Quality and Safety Supervision and Inspection Center Xi'an 710048)

At present, the quality of the elevator inspection has been widely concerned by the society, sample survey of inspection reports is an important part of the quality control of elevator inspection. In order to solve the scientifc and accuracy of the sample survey, this paper attempts to introduce the theory of stratifed sampling method for sample survey. The basic theory, feasibility and implementation steps of stratifed sampling for sample survey of elevator inspection reports were introduced, and a practical example was given.

Stratifed sampling method Elevator inspection reports Sample survey

X924

B

1673-257X(2017)08-0013-03

10.3969/j.issn.1673-257X.2017.08.004

黃鵬輝（1980～)，男，碩士，工程師，從事機電類特種設備的檢驗與研究工作。

黃鵬輝，E-mail： huits1980@163．com。

2017-03-30）