A CLASS OF PROJECTIVELY FLAT SPHERICALLY SYMMETRIC FINSLER METRICS

CHEN Ya-li,SONG Wei-dong

(1.School of Environmental Science and Engineering,Anhui Normal University,Wuhu 241000,China)

(2.School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

A CLASS OF PROJECTIVELY FLAT SPHERICALLY SYMMETRIC FINSLER METRICS

CHEN Ya-li1,SONG Wei-dong2

(1.School of Environmental Science and Engineering,Anhui Normal University,Wuhu 241000,China)

(2.School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

In this paper,we investigate the construction of projectively f l at Finsler metrics. By analysing the solution of the spherically symmetric projectively f l at equation,we construct new examples of projectively f l at Finsler metrics,and obtain the projective factor and f l ag curvature of spherically symmetric Finsler metrics to be projectively f l at.

projectively f l at;Finsler metric;spherically symmetric;projective factor;f l ag curvature

1 Introduction

It is an important problem in Finsler geometry to study and characterize projectively fl at Finsler metrics on an open domain in Rm.Hilbert’s 4th problem is to characterize the distance functions on an open subset in Rmsuch that straight lines are geodesics[5]. Regular distance functions with straight geodesics are projectively fl at Finsler metrics.A Finsler metric F=F(x,y)on an open subset U?Rmis projectively fl at if and only if it satis fi es the following equation

In Finsler geometry,the fl ag curvature K(P,y)is an analogue of the sectional curvature in Riemannian geometry.It is known that every projective Finsler metric is of scalar curvature,namely,the fl ag curvature K(P,y)=K(y)is a scalar function of tangent vectors y.Shen discussed the classi fi cation problem on projective Finsler metrics of constant fl ag curvature[14].The second author provided the projective factor of a class of projectively fl at general(α,β)-metrics[12]and studied a necessary and sufficient condition for a class of Finsler metric to be projectively fl at[13].Li proved the locally projectively fl at Finsler metrics with constant fl ag curvature K are totally determined by their behaviors at theorigin by solving some nonlinear PDEs.The classif i cations when K=0,K=-1,K=1 are given in an algebraic way[15].

For a Finsler metric F=F(x,y)on a manifold M,the geodesics c=c(t)of F in local coordinates(xi)are characterized by

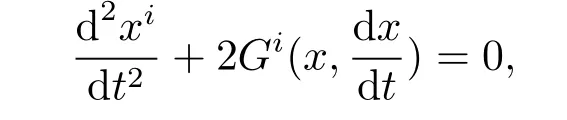
where(xi(t))are the coordinates of c(t)and Gi=Gi(x,y)are def i ned by

For a tangent plane P?TpM and a non-zero vector y∈TpM,the f l ag curvature K(P,y)is def i ned by

where P=span{y,u}.It is known that if F is projectively f l at,the spray coefficients of F are in the form Gi=Pyiwhere

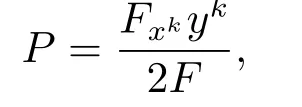
then F is of scalar curvature with f l ag curvature

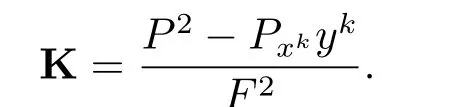
On the other hand,the study of spherically symmetric Finsler metrics attracted a lot of attention.Many known Finsler metrics are spherically symmetric[1,4,7,14,15,17].A Finsler metric F is said to be spherically symmetric(orthogonally invariant in an alternative terminology in[6])if F satisf i es

for all A∈O(m),equivalently,if the orthogonal group O(m)acts as isometrics of F.Such metrics were f i rst introduced by Rutz[16].

It was pointed out in[6]that a Finsler metric F on Bm(μ)is a spherically symmetric if and only if there is a function φ：[0,μ)×R→R such that

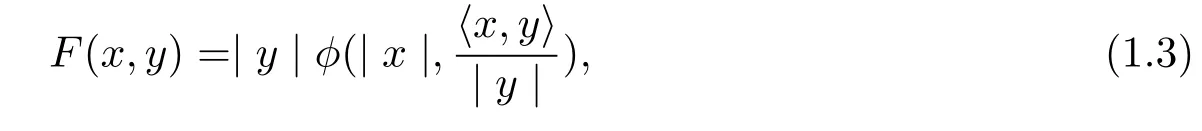
where(x,y)∈TRm(μ){0}.The spherically symmetric Finsler metric of form(1.3)can be rewritten as the following form[8]

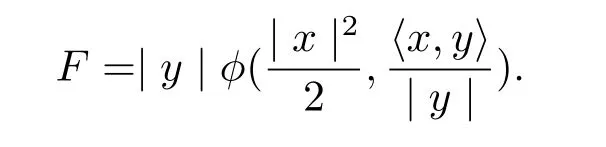
Spherically symmetric Finsler metrics are the simplest and most important general (α,β)-metrics[4].Mo,Zhou and Zhu classif i ed the projective spherically symmetric Finsler metrics with constant f l ag curvature in[2,9,10].A lot of spherically symmetric Finsler metrics with nice curvature properties were investigated by Mo,Huang and et al.[3,6-11].

An important example of projectively f l at Finsler metric was given by Berwald.It can be written as

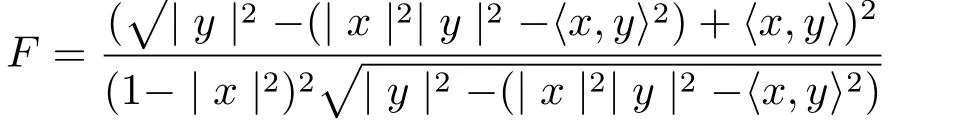
on the unit ball?Rm,where y∈TxBm?Rm.It could also be expressed as

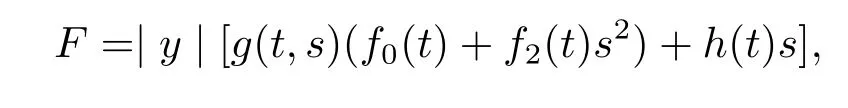
where

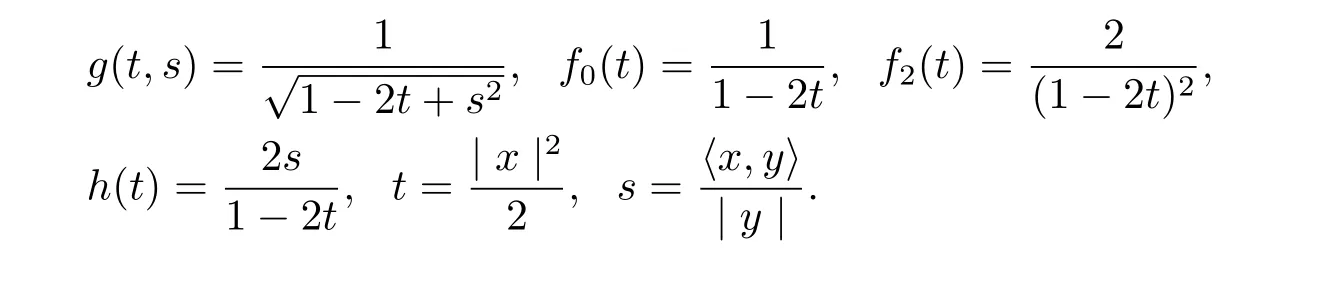
Inspired by the Berwald metric,we try to f i nd the solution of the projectively f l at eq.(1.1) in the following forms

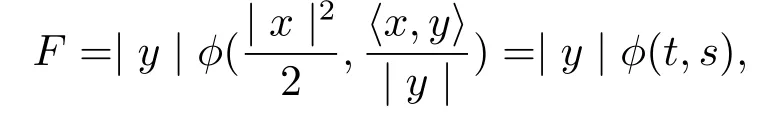
where

Through caculations,we have the following conclusions.

Theorem 1.1 Let φ(t,s)be a function def i ned by

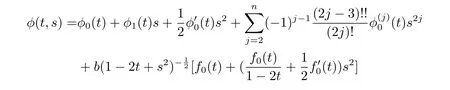
and f0(t)is a dif f erentiable function which satisf i es

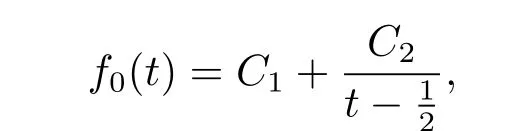
where b,C1,C2are constants and φ1is an any continuous function,φ0is a polynomial function of N degree wheredenotes the j-order derivative for φ0(t),φ(t,s)needs to satisfy φ-sφs＞0,when m=2.Moreover,the additional equality holds

when m≥3.Then the following spherically symmetric Finsler metric on Bm(μ)

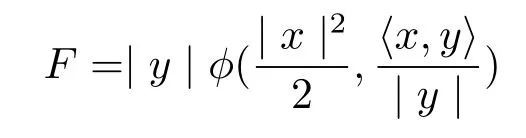
is projectively fl at.

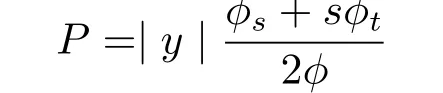
and its f l ag curvature K is given by

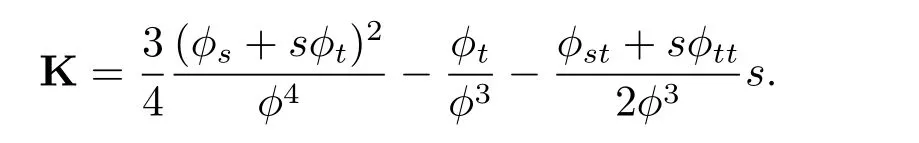
2 The Solutions of the Hamel Equation

In this section,we will construct a lot of projectively fl at Finsler metrics which contains the Berwald metric.From[8],we know that

Consider the spherically symmetric Finsler metricwhere φ=φ(t,s)is given by φ(t,s)=By a direct caculation,we get

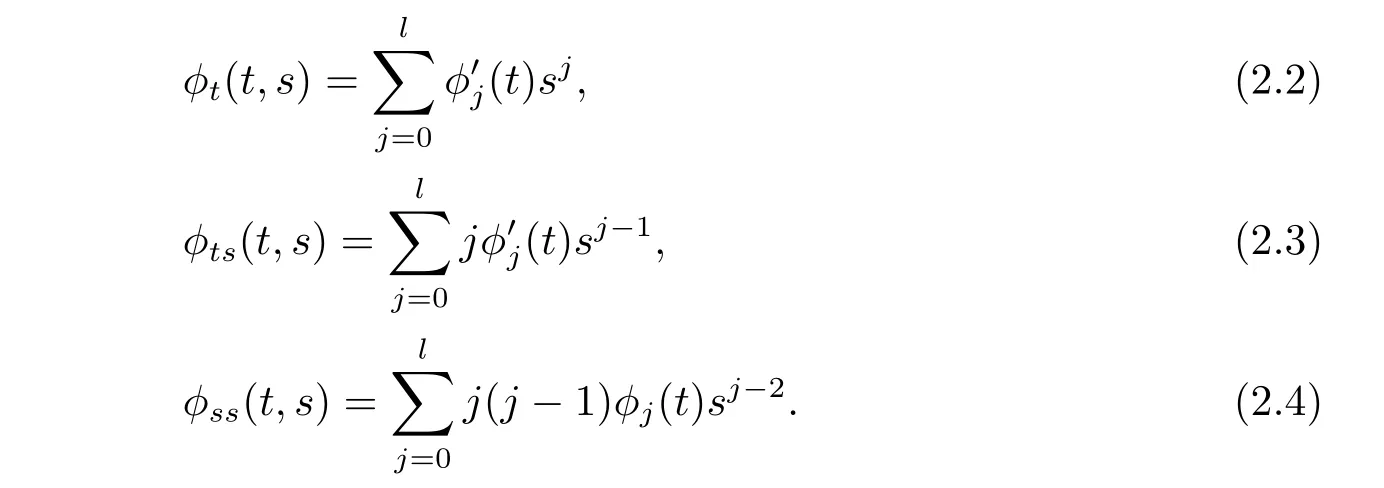
Plugging(2.2),(2.3),(2.4)into(2.1),the following equation is deduced,

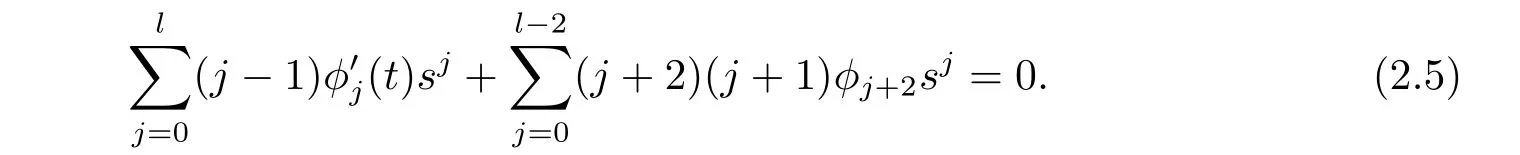
It is equivalent to

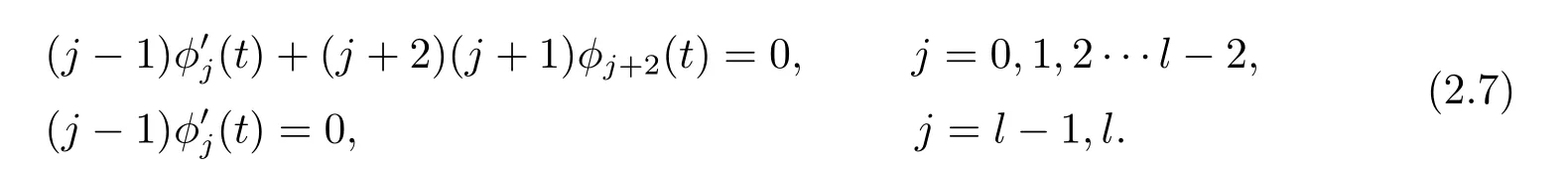
When j=0,from the f i rst equation of(2.7),we get

Similarity,taking j=1 and j=2,we obtain

If k=j+2,the f i rst equation of(2.7)is equivalent to

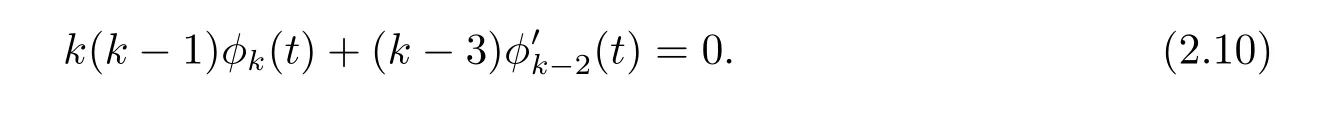
It is easy to see the recurrence fomula on φk(t)and φ′k(t),

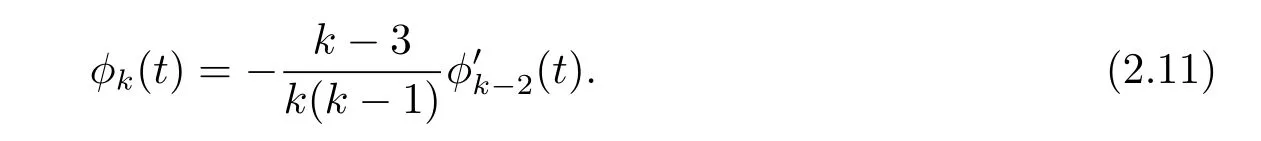
If k=odd,k≥3,then by(2.11),

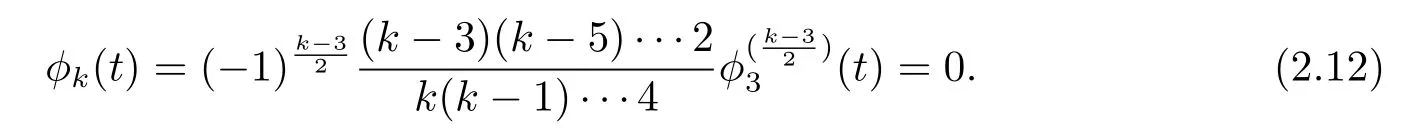
If k=even,k≥4,we have

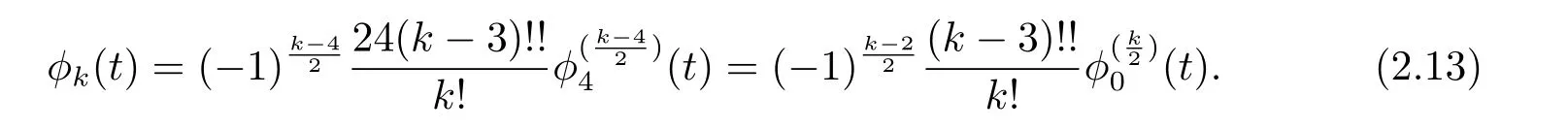
Case 1 k=odd≥5,setting l=2n+1,by the second equation of(2.7),

then it follows from(2.1),(2.12),(2.13),(2.14),

Case 2 k=even≥4,setting l=2n+2,by the second equation of(2.7),

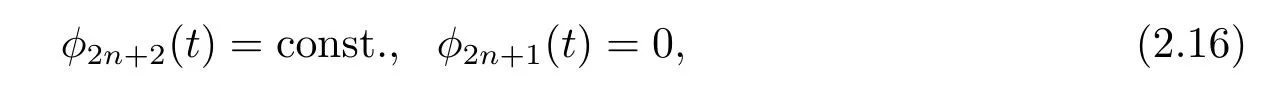
then it follows from(2.1),(2.12),(2.13),(2.16),

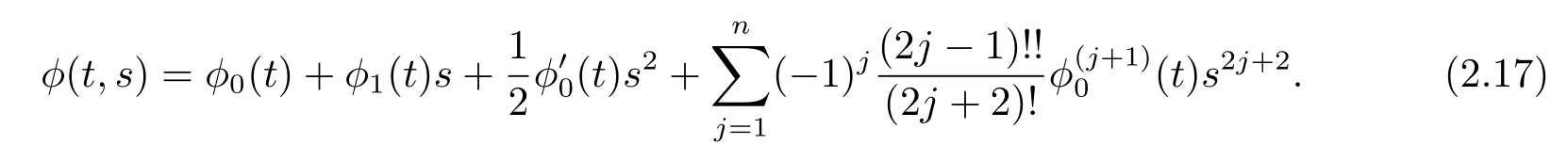
The case l∈{1,2,3}is similar.Through the above analysis,we obtain the following.

Multiplying g-ron the both sides of(2.24),then

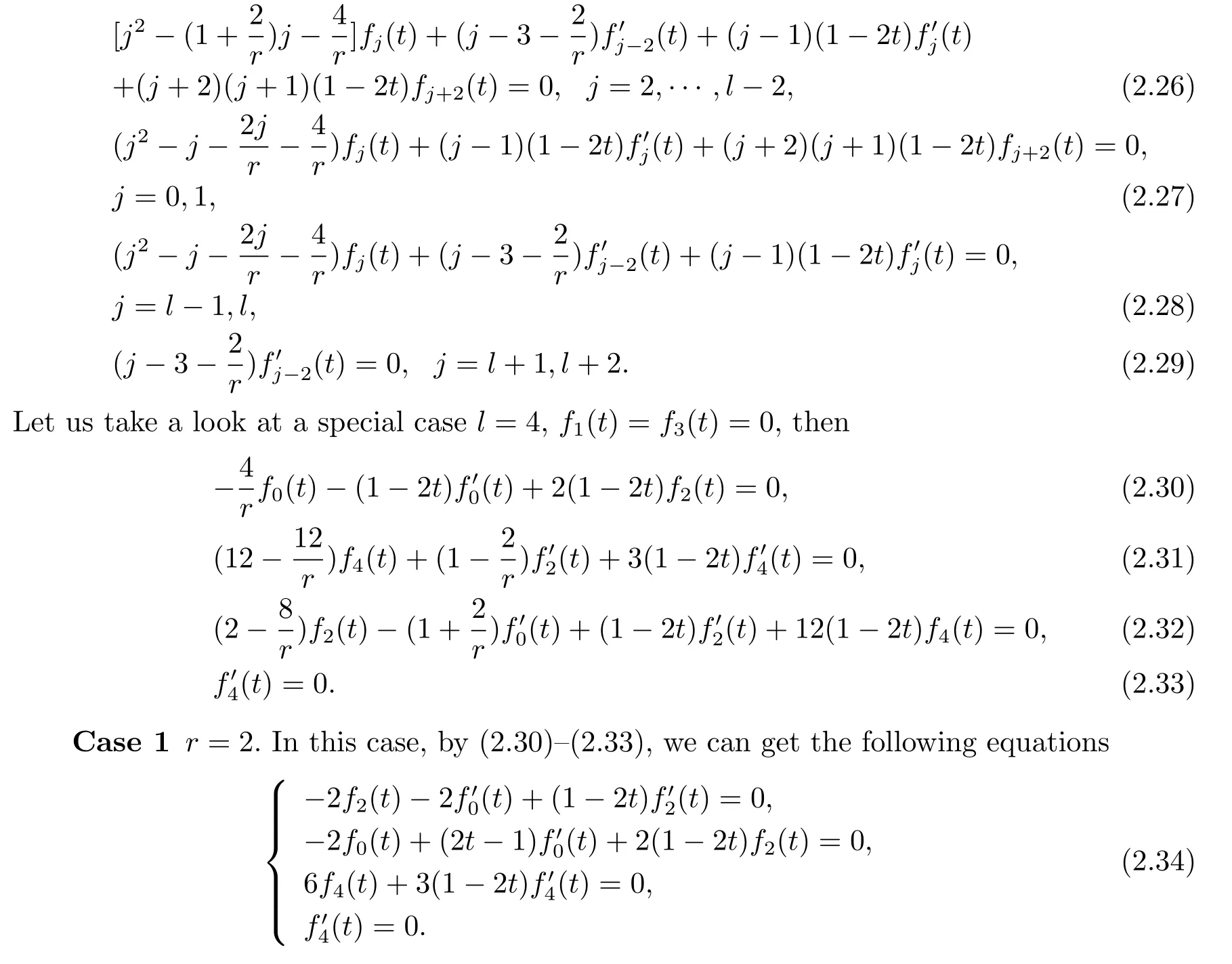
From(2.25),we obtain the following equationsSubstituting the fourth equation of(2.34)into the third equation of it,we have f4(t)=0. From(2.30),we obtain

Dif f erentiating(2.35),we get

Substituting(2.35),(2.36)into the f i rst equation of(2.34),we obtain that f0(t)satisf i es

Solving(2.37),we have

Plugging(2.39)into(2.32),we obtain

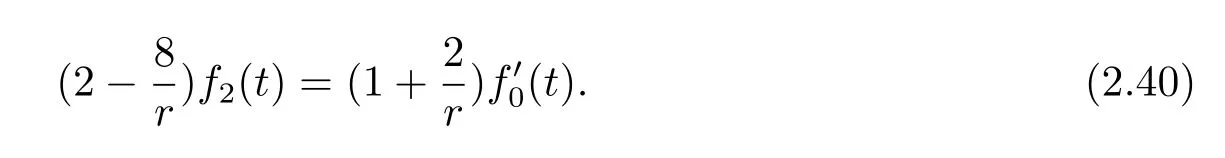
If r=4,f′0(t)=0,from(2.30),

Thus f0(t)and f2(t)can’t be constants at the same time,so in this case,r 6=4,together with(2.39),(2.40),(2.41),we know that f2(t)needs to satisfy the following

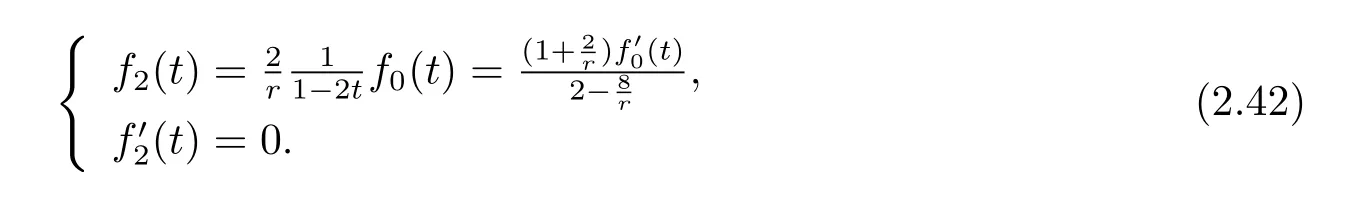
Through(2.42),we get that f0(t)needs to satisfy

From the f i rst equation of(2.43),

where C1is a constant.But the f0(t)in(2.44)doesn’t satisfy the second equation of(2.43) only if r=1,thus we can get the following proposition.

and f0(t)=C1(-1+2t),where b,C1are constants.

Case 3 r 6=2,f4(t)6=0.In this case,from the f i rst equation of(2.30),

Dif f erentiating(2.45),we have

From(2.32),we get

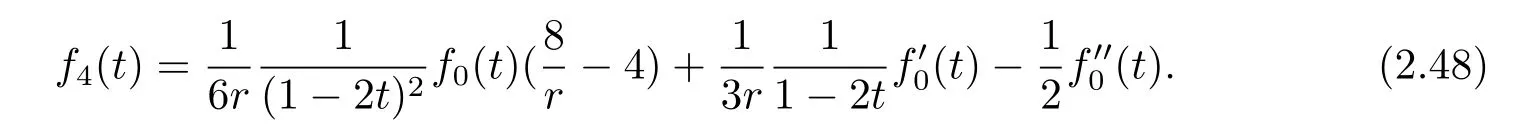
Dif f erentiating(2.48),we obtain

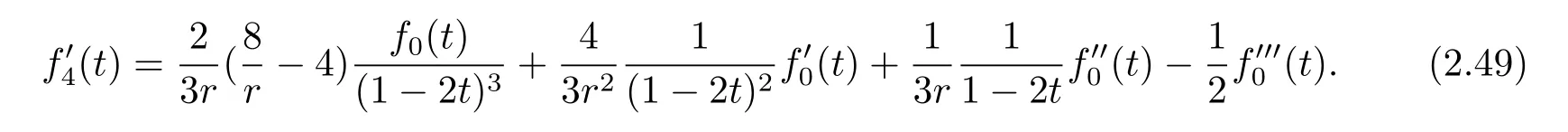
Plugging(2.33)into(2.31),we have

Thus from(2.50),no matter r=1 or not,

Combining the fourth equation of(2.33)and(2.51),we obtain that f0(t)satisf i es

Solving the f i rst equation of(2.52),we get

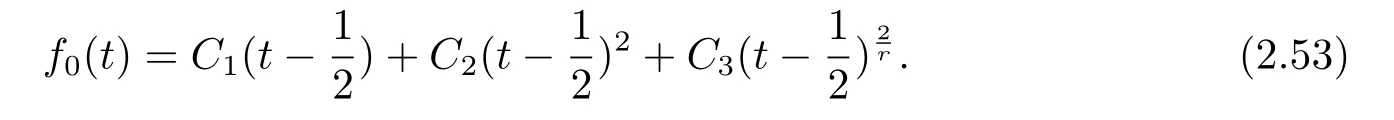
Solving the second equation of(2.52),we know

If r=1,C3=C6=0,two equations of(2.52)have the same solutions.Thus we have the following proposition.

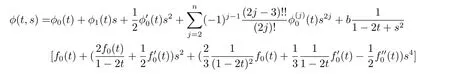
and f0(t)=are constants.

3 Proof of Theorems

φ(t,s)in Propositions 2.2,2.3,2.4 can’t ensure that F=|y|is a Finsler metric.In order to obtain projectively fl at Finsler metric,φ(t,s)in Propositions 2.2-2.4 needs to satisfy the necessary and sufficient condition for Fto be a Finsler metric for any α and β with kβxkα＜b0given by Yu and Zhu[4].In particular,considering F=|y|=|y|φ(t,s),then F is a Finsler metric if and only if the positive function φ satis fi es

when m≥3 or

when m=2.

Proof of Theorem 1.1 Combine Proposition 2.2,(3.1),(3.2)and the fundamental property of the projectively f l at equation(2.1).

Proof of Theorem 1.2 Combine Proposition 2.3,(3.1),(3.2)and the fundamental property of the projectively f l at equation(2.1).

Proof of Theorem 1.3 Combine Proposition 2.4,(3.1),(3.2)and the fundamental property of the projectively f l at equation(2.1).

Proof of Theorem 1.4 Suppose that

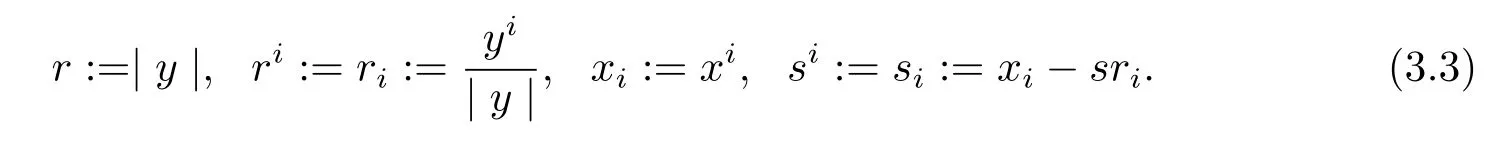
Direct computations yield that

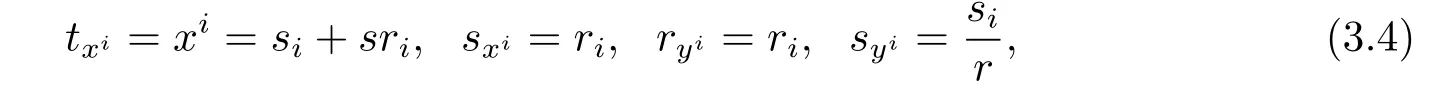
where we use of(3.3).By(3.3),(3.4),we get the following lemma.

Lemma 3.1 Let f=f(r,t,s)be a function on a domain U?R3.Then

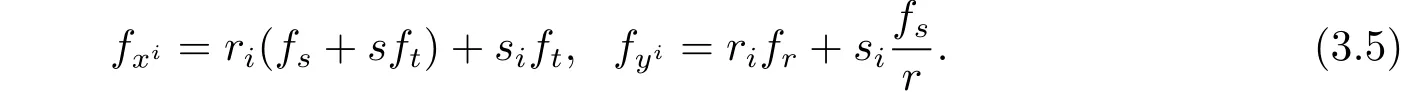
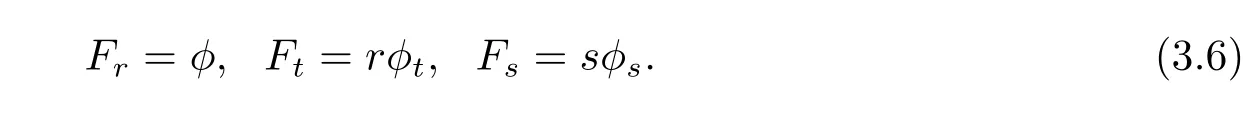
Note that siand riare positively homogeneous of degree 0 and 1.Hence

and we get

Thus from(3.7),(3.8),we have F0=Fxiyi=r2(φs+sφt),

Dif f erentiating(3.9),we know

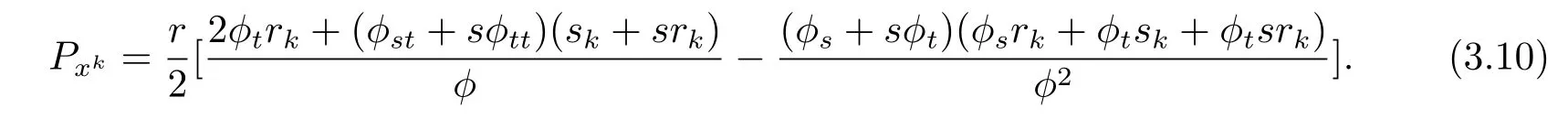
From(3.7),(3.10),we obtain

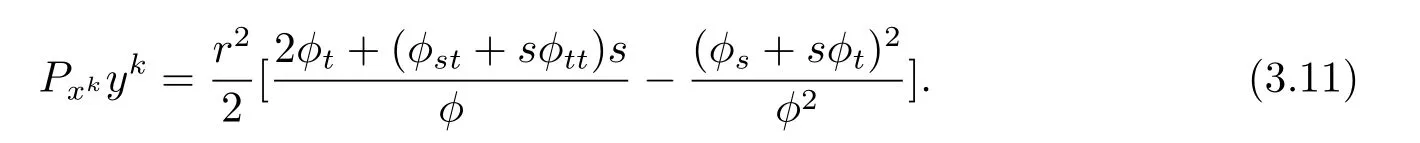
Thus using(3.9),(3.11),we have

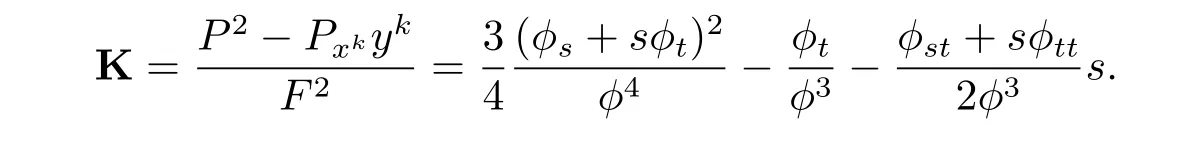
Theorem 1.4 can be achieved.

[1]Chern S S,Shen Z M.Riemann-Finsler geometry[M].Hackensack,NJ：World Sci.Publ.Co.Pvt. Ltd.,2005.

[2]Mo Xiaohuan,Zhou Linfeng.The curvatures of spherically symmetric Finsler metrics in Rn[J]. Trans.Res.Board 91st Ann.Meet.,2012,139：94-103.

[3]Huang Libing,Mo Xiaohuan.On spherically symmetric Finsler metrics of scalar curvature[J].J. Geom.Phy.,2012,62(11)：2279-2287.

[4]Yu Changtao,Zhu Hongmei.On a new class of Finsler metrics[J].Dif f.Geom.Appl.,2011,29(2)：244-254.

[5]Hilert D.Mathematical problems[J].Bull.Amer.Math.Soc.,2001,37：407-436.Reprinted from Bull.Amer.Math.Soc.,1902,8：437-439.

[6]Huang Libing,Mo Xiaohuan.Projectively f l at Finsler metrics with orthogonal invariance[J].Ann. Polon.Math.,2013,107：259-270.

[7]Yu Changtao.On dually f l at Randers metrics[J].Nonl.Anal.：The.Meth.Appl.,2014,95：146-155.

[8]Huang Libing,Mo Xiaohuan.On some explicit constructions of dually f l at Finsler metrics[J].J. Math.Anal.Appl.,2013,405(2)：565-573.

[9]Zhou Linfeng.Projective spherically symmetric Finsler metrics with constant f l ag curvature in Rn[J]. Geom.Dedicata,2012,158(1)：353-364.

[10]Mo Xiaohuan,Zhu Hongmei.On a class of projectively f l at Finsler metrics of negative constant f l ag curvature[J].Intern.J.Math.,2012,23(8)：84-85.

[11]Guo Enli,Liu Huaifu,Mo Xiaohuan.On spherically symmetric Finsler metrics with isotropic Berwald curvature[J].Intern.J.Geom.Meth.Modern Phy.,2013,10(10)：603-610.

[12]Song Weidong,Wang Xingshang.A new class of Finsler metrics with scalar f l ag curvature[J].J. Math.Res.Appl.,2012,32(4)：485-492.

[13]Song Weidong,Zhu Jingyong.A class of projectively f l at Finsler metrics[J].J.Math.Res.Appl., 2013,33(6)：737-744.

[14]Shen Zhongmin.Projectively f l at Finsler metrics of constant f l ag curvature[J].Trans.Amer.Math. Soc.,2003,355(4)：1713-1728.

[15]Li Benling.On the classif i cation of projectively f l at Finsler metrics with constant f l ag curvature[J]. Adv.Math.,2014,257(2)：266-284.

[16]Rutz S.Symmetry in Finsler spaces[J].Contem.Math.,1996,196：289-300.

[17]Chen Yali,Song Weidong.A class of dually f l at spherically symmetric Finsler metrics[J/OL].J. Math.,http：//www.cnki.net/kcms/detail/42.1163.O1.20150409.1408.002.html.

一類射影平坦的球?qū)ΨQ的芬斯勒度量

陳亞力1,宋衛(wèi)東2

(1.安徽師范大學(xué)環(huán)境科學(xué)與工程學(xué)院,安徽蕪湖241000)
(2.安徽師范大學(xué)數(shù)學(xué)計算機(jī)科學(xué)學(xué)院,安徽蕪湖241000)

本文研究了射影平坦芬斯勒度量的構(gòu)造問題.通過分析射影平坦的球?qū)ΨQ的芬斯勒度量的方程的解,構(gòu)造了一類新的射影平坦的芬斯勒度量,并得到了射影平坦的球?qū)ΨQ的芬斯勒度量的射影因子和旗曲率.

射影平坦;芬斯勒度量;球?qū)ΨQ;射影因子;旗曲率

O186.1

A

0255-7797(2017)05-0932-13

?Received date：2015-04-21Accepted date：2015-12-09

Supported by the National Natural Science Foundation of China(11071005); the Research Culture Funds of Anhui Normal University(2016XJJ017).

Biography：Chen Yali(1990-),femal,born at Wuhu,Anhui,master,major in dif f erential geometry and its applications.

2010 MR Subject Classif i cation：53B40;53C60;58B20