基于三次B′ezier基函數插值的GM(1,1)模型背景值優化研究

董克,呂文元

(1.上海理工大學管理學院,上海200093)

(2.安徽廣播電視大學公共基礎部,安徽合肥230022)

基于三次B′ezier基函數插值的GM(1,1)模型背景值優化研究

董克1,2,呂文元1

(1.上海理工大學管理學院,上海200093)

(2.安徽廣播電視大學公共基礎部,安徽合肥230022)

本文研究了傳統灰色GM(1,1)模型存在模型精度不高的問題.利用帶形狀參數的三次B′ezier基函數,給出插值函數的表達式,并結合復化梯形公式,給定誤差限的方法,獲得了比傳統灰色GM(1,1)模型更高精度的結果.推廣了傳統灰色GM(1,1)預測模型的結果.

GM(1,1)模型;復化梯形公式;背景值;插值函數

1 引言

自上個世紀80年代鄧聚龍教授提出灰色系統理論[1]以來,灰色系統理論在許多領域得到了廣泛的應用和發展[2-6].GM(1,1)模型是灰色系統理論的核心內容之一,它主要針對“小樣本、貧信息”的不確定系統.但是,傳統的GM(1,1)模型具有預測精度不高的問題,如何提高GM(1,1)模型的預測精度,已經成為廣大研究人員最關注的問題.而影響GM(1,1)模型預測精度的主要因素有初始條件的選取、背景值的重構和參數估計方法的改進,其中背景值的重構,具有決定性的作用.傳統方法實質上是使用緊鄰均值構造背景值,誤差通常較大,從而導致模型預測的偏差也較大,預測精度自然達不到要求.近年來不少學者提出了提高灰色GM(1,1)模型預測精度的方法,文獻[7-9]從背景值的幾何意義出發,進行了系列研究,提出了若干種背景值的構造方式;文獻[10]利用拉格朗日插值公式對背景值進行重構,對傳統模型的背景值進行了改進,并利用最小二乘法對初始值進行了優化;李俊蜂等[11]提出一種基于數值分析中的插值法和Newton-Cotes公式的背景值構造方法.但是,眾所周知,當n較大時,高次插值會出現Runge現象,造成的誤差可能會很大,故不能通過提高階的方法來提高求積精度;文獻[12]提出一種利用梯形面積和矩形面積相結合的正負誤差補償方法進行背景值的重構方法,取得一定的效果,但是n1值的選取很難把握;文獻[13]提出用Simpson公式構造模型背景值的方法,擬合精度在一定程度上得到了改進;王曉佳等[14]提出利用分段插值函數與Newton插值函數相結合的組合插值方法,但分段過程比較繁瑣;蔣詩泉等[15]提出基于復化梯形公式的背景值優化方法,但是僅選取區間等分數n=4的情形,而對于n值取更大的情況未予以考慮.

文中構造出帶形狀參數的三次B′ezier基函數,然后給出插值函數,提出了基于復化梯形公式的背景值構造方法,給定誤差限,結合提出的優化算法,計算出對應的背景值,提高了GM(1,1)模型的預測精度.以工程實際應用中無鎳鑄造裝甲鋼的斷裂韌度值為例,實例研究表明,提出的方法不僅提高了GM(1,1)模型的預測精度,并且擴展了GM(1,1)模型的應用范圍.

2 模型建立

給定x(0)(t)={x(0)(1),x(0)(2),···,x(0)(n),x(0)(t)＞0,i=1,2,···,n}為原始序列,可以建立基本的GM(1,1)模型,將序列x(0)(t)進行一次累加(1-AGO),得到累加序列x(1)(t)為x(1)(t)={x(1)(1),x(1)(2),···,x(1)(n),···,x(1)(n)},其中

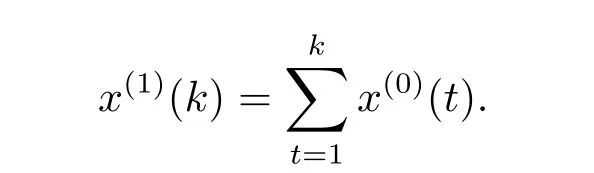
序列的白化微分方程為

灰色GM(1,1)模型的基本形式如下

利用最小二乘法求解參數a和b,

x(1)(k)的GM(1,1)模型為

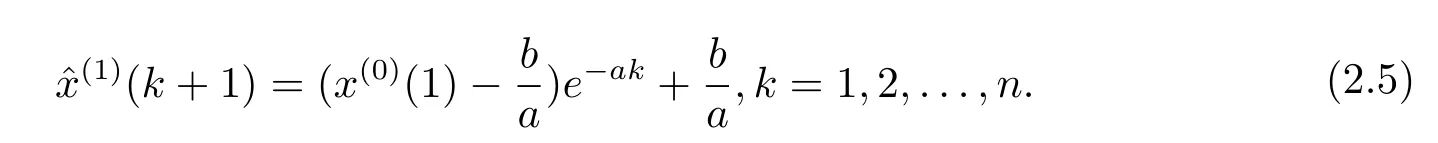
由于預測方程是對累加數據序列x(1)(t)的預測,進行累減還原,則可以得到原始數據序列的預測公式

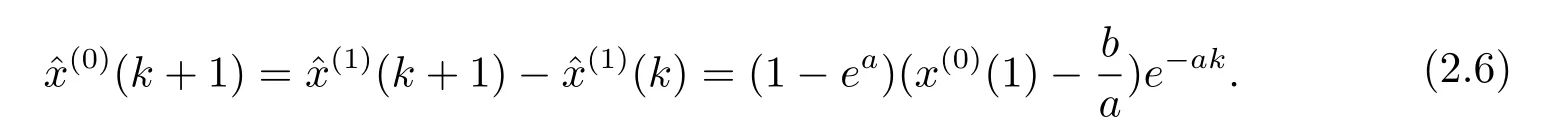
從公式(2.6)可以看出,模型的擬合預測精度取決于參數a,b及初始值x(0)(1)的值.而參數a,b的值又取決于原始數據序列和背景值z(1)(k).因此,背景值構造公式的合理性直接影響模型預測精度.傳統的背景值計算實質上是梯形的面積,而實際值正如圖1所示,應該等于曲線x(1)(t)在區間[k-1,k]上與t軸圍成的面積,這也是傳統背景值計算公式的誤差產生的根源所在.將積分區間分成若干小區間,在每個小區間上用低階求積公式,然后將這些小區間上的積分值相加作為函數在整個區間上的積分的近似值,這就是復化求積的思想.下述內容將給出利用三次B′ezier基函數構造插值函數,結合復化梯形公式的GM(1,1)模型的背景值優化方法及算法.

圖1：傳統GM(1,1)模型誤差來源圖

3 灰色GM(1,1)模型背景值的優化

3.1 插值基函數的構造

1962年,法國雷諾(Renault)汽車公司的工程師B′ezier提出了一種新的方法用來構造著名的B′ezier曲線[16],設計人員只需要移動控制多邊形的控制節點就可以方便地修改曲線的形狀,而且形狀的變化完全在預料之中,但是它無法插值控制節點,并且需要移動控制節點的位置來改變曲線的形狀.下述將構造出一種帶形狀參數λ的三次B′ezier基函數,不用調節控制多邊形的節點位置,只須通過調節形狀參數λ的值,即可調節設計曲線的形狀,而且當參數值λ=2時,曲線插值中間控制節點.文中將利用參數λ=2時,三次B′ezier基函數的插值性質,來構造插值函數,從而計算GM(1,1)模型的背景值.

定義3.1[1]對t∈[0,1],λ∈R,則稱關于t的多項式

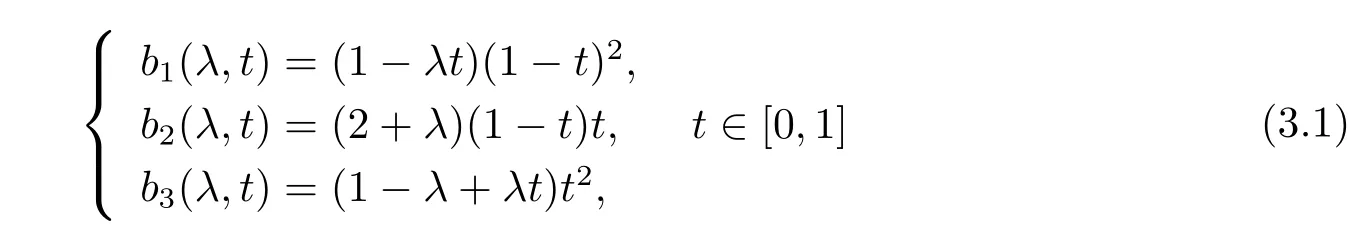
為帶形狀參數λ的三次B′ezier基函數.當λ=0時,基函數退化為二次B′ezier基函數.因此它是二次B′ezier基函數的擴展.當λ=2時,公式(3.1)將簡化為

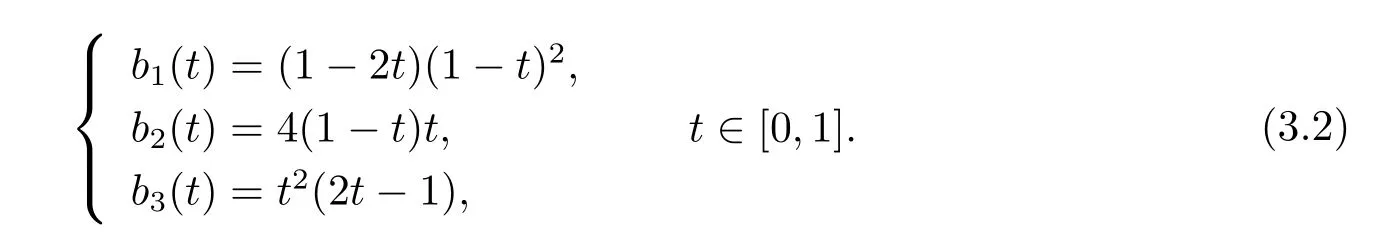
若任意給定三個插值節點x(1)(1),x(1)(2),x(1)(3),插值函數為

當t=0.5時,基函數b1(t),b3(t)的值均為0,而b2(t)的值為1,則公式(3.3)為f(0.5)= x(1)(2),說明函數f(t)是插值于中間控制節點的.圖2為給定三個插值節點(-2,0),(0,1), (2,0),所得到的插值函數圖形,從圖中可以看出,插值函數是插值中間控制點的.

圖2：利用插值基函數構造的插值函數圖形

定義3.2設在區間[a,b]上,給定三個插值節點(k,x(1)(k)),(k+1,x(1)(k+1)),(k+ 2,x(1)(k+2)),再利用公式(3.2)所定義的基函數,則可得區間[a,b]上的插值函數

3.2 復化梯形公式

定義3.3[17]將區間[a,b]劃分為n等份,分點xk=a+kh,h==0,1,···,n,在每個子區間,(k=0,1,···,n-1)上采用梯形公式

定理3.2對復化梯形公式Tn,若將區間[a,b]進行2n等分,則得到T2n：

由定義3.1和定理3.2可得

在使用復化梯形公式進行求積計算時,必須先給出步長h或者等分數n的值,步長h取得太大,則精度無法滿足要求;步長取得太小,則導致計算量過大.在使用復化梯形進行實際計算時,給定誤差值ε,用|T2n-Tn|＜ε成立與否,作為計算的終止條件.如果滿足給定的誤差限,則取T2n作為所求的值;否則,再將子區間對分,進行計算,直到滿足給定的誤差要求為止.下一部分將給出利用復化梯形公式(3.6)進行背景值優化的算法.

3.3 算法步驟

步驟1輸入原始序列x0(i),x0(i)＞0,i=1,2,···,n,ε以及端點a,b的值,置

步驟2計算利用公式(3.4),計算插值函數,并計算

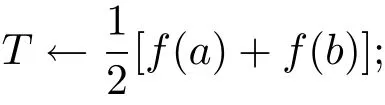
步驟3計算

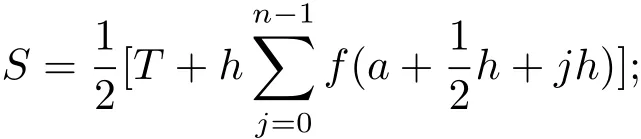
其他,轉步驟5;

步驟5轉向T;結束.

3.4 算法時間復雜度分析

傳統灰色GM(1,1)模型的背景值z(1)(k)的計算是與規模問題n無關的常數,所以時間復雜度為O(1).但對于使用復化梯形公式進行優化計算的背景值來說,時間復雜度與區間等分數n相關,時間復雜度為O(n).

4 算例分析

以無鎳鑄造裝甲鋼鋼的斷裂韌度值為例[18],分別計算傳統灰色GM(1,1)模型和所提出的優化GM(1,1)模型在回火溫度為600°C時試樣斷裂韌度的預測值,以溫度為200°C, 300°C,400°C,500°C時的斷裂韌度值數據作為原始數據,對溫度為600°C時的韌度值進行預測,并以600°C時的實際數據作為檢驗數據.

給定誤差限ε的值,即可以利用提出的算法,進行背景值計算.此處取ε=0.01,選取插值節點(1,x(1)(1)),(2,x(1)(2)),(3,x(1)(3))為例,利用上述給出的插值函數公式及背景值優化算法,得到z1(2)=149.226.同理可以得到z1(3)=220.098,z1(4)=323.240.

將利用復化梯形公式優化算法計算得到的背景值,代入優化的灰色GM(1,1)模型,即可得到預測值,并計算出它的相對誤差值.可以看出,與傳統的GM(1,1)模型比較,優化后的灰色GM(1,1)模型的平均相對誤差為4.5457%,比傳統的GM(1,1)模型降低了0.6235%,有明顯改進.預測誤差也由16.8118%降低至13.1823%,精度提高了3.6295%.可見,文中所提出的方法與傳統模型方法相比,具有一定的優越性.結果見表1.

表1：斷裂韌度值預測比較表

5 結語

文中給出了基于帶三次B′ezier插值基函數插值,結合復化梯形公式的背景值的優化方法,給定誤差限,利用給出的算法,即可計算出灰色GM(1,1)模型的背景值.與傳統的背景值構造方法采用Lagrange[10]、Newton[11]插值或者組合插值[13]相比,文中構造出一組插值基函數,方法簡便,只須將累加序列節點,代入即可求出插值函數,易于操作.實例研究表明,文中提出的優化模型及算法的有效性,比傳統的灰色GM(1,1)模型誤差有明顯的改進,擴大了GM(1,1)模型的適應性,優化后的GM(1,1)模型更合理,有助于提高GM(1,1)模型的預測精度,擴展了GM(1,1)模型的應用范圍.

[1]鄧聚龍.灰色理論基礎[M].武漢：華中理工大學出版社,2002.

[2]肖新平,毛樹華.灰預測與決策方法[M].北京：科學出版社,2013.

[3]王治禎.灰色系統及模糊數學在環境保護中的應用[M].哈爾濱：哈爾濱工業大學出版社,2007.

[4]Liu S F,Lin Y.Grey system：theory and applications[M].London：Springer,2011.

[5]曹昶,樊重俊,胡兆龍.基于正弦函數變換的灰色預測模型研究及其應用[J].數學雜志,2013,33(4)：697-701.

[6]湯旻安,李瀅.基于數據變換的優化GM(1,1)模型[J].數學雜志,2015,35(4)：957-962.

[7]譚冠軍.GM(1,1)模型的背景值構造方法和應用(I)[J].系統工程理論與實踐,2000,20(4)：98-103.

[8]譚冠軍.GM(1,1)模型的背景值構造方法和應用(II)[J].系統工程理論與實踐,2000,20(5)：125-132.

[9]譚冠軍.GM(1,1)模型的背景值構造方法和應用(III)[J].系統工程理論與實踐,2000,20(6)：70-74.

[10]唐萬梅,向長合.基于二次插值GM(1,1)模型預測方法的改進[J].中國管理科學,2006,14(12)：109-112.

[11]李俊蜂,戴文戰.基于插值和Newton-Cotes公式的GM(1,1)模型的背景值構造新方法及應用[J].系統工程理論與實踐,2002,10：122-126.

[12]戴文戰,熊偉,楊愛萍.基于函數變換及背景值優化的灰色建模[J].浙江大學學報(工學版),2010,44(7)：1368-1372.

[13]何滿喜,王勤.用Simpson公式構造背景值的GM(1,1)建模新方法[J].經濟數學,2011,28(12)：101-104.

[14]王曉佳,楊善林.基于組合插值的GM(1,1)模型預測方法的改進與應用[J].中國管理科學,2012,20(4)：130-134.

[15]蔣詩泉,劉思峰,周興才.基于復化梯形公式的GM(1,1)模型背景值的優化[J].控制與決策,2014, 29(12)：2221-2225.

[16]王國瑾,汪國昭,鄭建民.計算機輔助幾何設計[M].北京：高等教育-施普林格出版社,2001.

[17]李慶揚,王能超,易大義.數值分析[M].北京：清華大學出版社,2008.

[18]馬德林.常用黑色金屬材料斷裂力學性能參數手冊[M].北京：兵器工業出版社,1994.

OPTIMIZATION OF BACKGROUND VALUE IN GM(1,1)BASED ON CUBIC B′EZIER BASIS FUNCTION INTERPOLATION

DONG Ke1,2,LV Wen-yuan1

(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)
(2.Department of Foundation,Anhui Radio&TV University,Hefei 230022,China)

In this paper,we study the accuracy of GM(1,1)forecasting model.In combination with compound trapezoid formula,cubic B′ezier basis function method with shape parameter interpolation function expression is presented to solve the problem of low precision of traditional GM(1,1).Given error limits,the model which given in this paper can obtain more precision than traditional GM(1,1)model,which enlarge the application scope of GM(1,1)model.

GM(1,1)model;compound trapezoid formula;the background value;interpolation function

O175.2

A

0255-7797(2017)05-1022-07

2015-07-01接收日期：2015-12-23

上海市浦江人才計劃項目(14PJC077);安徽廣播電視大學青年教師基金項目(qn15-19).

董克(1982-),男,安徽蚌埠,講師,主要研究方向：灰色理論及其應用.

2010 MR Subject Classif i cation：35F10