基于EV模型ND樣本加權和的相合性

蘭沖鋒

(阜陽師范學院經濟學院,安徽阜陽236037)

(區域物流規劃與現代物流工程安徽省重點實驗室,安徽阜陽236037)

基于EV模型ND樣本加權和的相合性

蘭沖鋒

(阜陽師范學院經濟學院,安徽阜陽236037)

(區域物流規劃與現代物流工程安徽省重點實驗室,安徽阜陽236037)

本文研究變系數EV模型的ND樣本加權和的相合性問題.利用ND序列的Bernstein型不等式和截尾的方法,獲得了ND樣本加權和的強、弱相合性,推廣了獨立隨機變量加權和的相合性.

變系數EV模型;ND樣本;加權和;相合性

1 引言

在一維線性結構關系EV(errors-in-variables)模型[1]中,如果參數a,b是實變量t的有界連續函數a(t),b(t),t∈(0,1),(b(t)6=0),可得到下列變系數一維線性結構關系的EV模型

其中X,Y是隨機變量,(?,u)是測量誤差,t是一實變量,可以是溫度、時間等,假定t在一個閉區間上變化,可通過變換使得t∈[0,1].

目前關于變系數EV模型的討論還處在起步階段,但是也取得了一些成果,如歐陽[2]初步研究了這類模型,他利用加權正交回歸最小二乘法給出了該模型的一維線性結構的參數估計,并得到了該估計的強、弱相合性;崔[3]給出了變系數線性EV模型參數的調整加權最小二乘估計及其漸近性質;方和胡[4]討論了核實數據下非線性EV模型中經驗似然降維推斷等.而本文則研究變系數EV模型的ND樣本加權和的相合性問題,為此先討論EV模型的權函數問題.

設t0∈(0,1),要對t0處的a(t0),b(t0)進行參數估計.然而不可能在t0處作n次觀測,只能在t0處附近作n次觀測.設t1,t2,···,tn是[0,1]上n個設計點,滿足

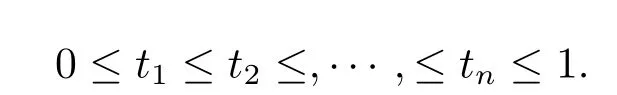
對每個點ti處(Y,X)作觀測,得到n組觀測值(Yi,ti,Xi)(i=1,2,···,n).當利用這n組觀測值來估計t0處的參數a(t0),b(t0)時,此時應該注意到ti處的觀測值(Yi,ti,Xi)(i= 1,2,···,n)相對于t0來說它們的重要程度并不一樣,這種重要程度可用實變量ti的權函數Wni(t0)來度量.下面給出權函數的定義.

設(Yi,ti,Xi)(i=1,2,···,n)是取自母體(Y,X)的樣本,t1,t2,···,tn是[0,1]上的n個設計點,t0是(0,1)內的某一個點,實變量t1,t2,···,tn的函數Wni(t0)=Wni(t0,t1,t2,···,tn) (i=1,2,···,n)稱為實變量權函數(簡稱為權函數),如果它滿足

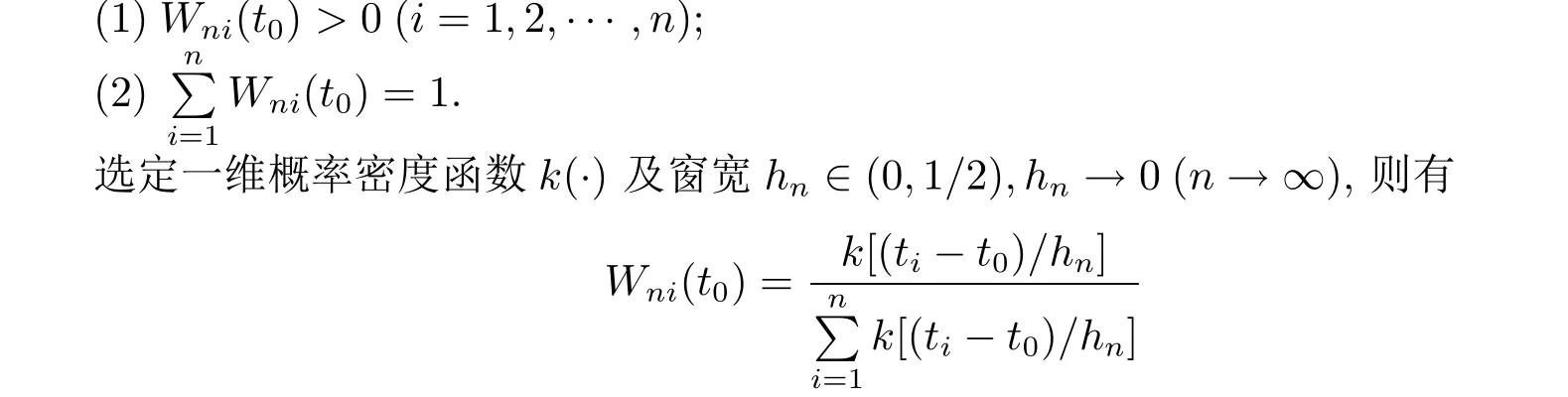
為權函數,稱之為核權函數.

在文[5]中提出了這樣一個問題：在何種條件下,當n→∞時有

如果?n≥2,X1,X2,···,Xn都是ND的,則稱隨機變量列{Xn,n≥1}是ND列.

文獻[9]舉例說明了NA序列一定是ND序列,但ND序列不一定是NA序列,這說明ND序列是比NA序列更弱、更廣泛的一種隨機變量序列.因此,對ND列的研究在理論和實踐中都是十分有意義的.自從1993年Bozorgnia等[8]提出ND相依概念以來,已經引起了越來越多的學者的關注,也取得了許多的研究成果,例如文獻[8-10]等.

2 引理

為了得出本文的主要結論,本節先給出一些相關的引理.

引理1[8]設{Xn,n≥1}是ND的,?m≥2,A1,A2,···,Am是集合{1,2,···,n}的兩兩不交的非空子集.如果fi,i=1,2,···,m是對每個變元都非降(或都非升)的函數,則f1(Xj,j∈A1),f2(Xj,j∈A2),···,fm(Xj,j∈Am)仍是ND的.

引理2[8]設隨機變量{Xn,n≥1}是ND列,則

3 主要結果及證明

定理1設{Y,Yi,i≥1}為同分布的ND樣本序列,且存在M＞0,使得Var(Y)≤M,若對任意實變量核權函數存在正數C,使得

則有

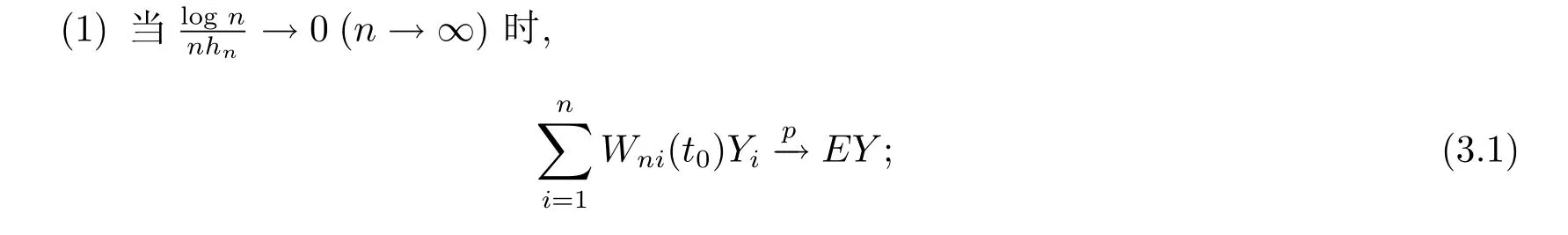
[1]Cui H,Chen S X.Empirical likelihood conf i dence region for parameter in the errors-in-variables models[J].J.Multi.Anal.,2003,84(1)：101-115.

[2]歐陽光.變系數線性結構關系EV模型的參數估計[J].應用數學學報,2005,28(1)：73-85.

[3]崔恒建.變系數線性EV模型參數的調整加權最小二乘估計及其漸近性質[J].系統科學與數學,2007, 27(1)：82-92.

[4]方連娣,胡鳳霞.核實數據下非線性EV模型中經驗似然降維推斷[J].數學雜志,2012,32(1)：113-120.

[5]陳希孺,王松桂.近代實用回歸分析[M].南寧：廣西人民出版社,1984,237-247.

[6]歐陽光.獨立隨機變量序列加權和的相合性[J].數學理論與應用,2005,25(1)：109-113.

[7]付艷莉,吳群英.NA同分布序列加權和的相合性[J].吉林大學學報(理學版),2010,48(1)：57-62.

[8]Bozorgnia A,Patterson R F,Taylor R L.Limit theorems for ND r.v.’s[R].Athens：University of Georgia,1993.

[9]Wu Q Y,Jiang Y Y.The strong consistency of M estimator in a linear model for negatively dependent random samples[J].Commun.Stat.：The.Meth.,2011,40(3)：467-491.

[10]Wu Q Y.Complete convergence for negatively dependent sequences of random variables[J].J.Inequ. Appl.,2010,Article ID 507293.

CONSISTENCY OF WEIGHTED SUMS FOR NEGATIVELY DEPENDENT SAMPLES BASED ON EV MODEL

LAN Chong-feng
(School of Economics,Fuyang Normal College,Fuyang 236037,China)
(Anhui Provincial Key Laboratory Regional Logistics Planning and Modern Logistics Engineering, Fuyang 236037,China)

In this paper,we discuss consistency of weighted sums for negatively dependent samples based on varying-coefficient EV model.By applying Bernstein type inequality for negatively dependent sequences and truncation methods,the strong and weak consistency of weighted sums for negatively dependent samples are obtained,which extend consistency of weighted sums for independent random variables.

varying-coefficient EV model;negatively dependent samples;weighted sums; consistency

O212.2

A

0255-7797(2017)05-1047-07

2014-01-24接收日期：2015-04-21

國家自然科學基金資助(71571174);安徽省高校自然科學研究重點項目基金資助(KJ2016A876;KJ2015A182)

蘭沖鋒(1981-),男,安徽阜陽,講師,主要研究方向：概率極限理論.

2010 MR Subject Classif i cation：62D05