空間任意方向圓柱面擬合方法

褚建春 張澤峰

(蘇州市測繪院有限責任公司，江蘇 蘇州 215000)

空間任意方向圓柱面擬合方法

褚建春 張澤峰

(蘇州市測繪院有限責任公司，江蘇 蘇州 215000)

提出了一種新的簡便可行的圓柱面擬合算法,利用兩臺無棱鏡全站儀架設在圓柱面的不同方向，分別獲取圓柱面上均勻分布的若干坐標點，再利用三維坐標轉換原理將這些坐標點轉換到統一坐標系統內。根據圓柱面的幾何原理，通過對圓柱面的位置和方向等幾何參數賦予任意值，利用最小二乘原理求出參數值來確定圓柱面，并評定圓柱面的圓度值。同時，將本方法的計算結果與其他方法進行對比分析，發現計算結果差異不大，精度大致相同，這也就驗證了本方法的可行性和正確性。

圓柱面擬合，三維坐標轉換，圓度，最小二乘原理

0 引言

在工業檢測和逆向工程中，曲面擬合是一個經常涉及到的實際問題。實物的形狀通常用數學公式描述，通過對其表面點進行三維坐標采樣，再根據數學模型擬合出實物表面在空間坐標系中的幾何方程[1,2]。在曲面擬合中，圓柱面的擬合比較常見，該過程要確定圓柱面的幾何參數，主要方法有高斯圖、遺傳算法、特征值法以及幾何法。

本文提出一種快速簡便的圓柱面擬合方法，并與文獻[6]中的方法進行比較分析，驗證該方法的可行性。該方法來擬合圓柱面時，在對誤差方程進行適當的變換后，可任意選取平差過程中參數的初始值。

1 坐標測量與轉換

1.1 坐標測量

利用全站儀無棱鏡模式采集圓柱面上點的三維坐標。由于圓柱面為三維立體表面，利用一臺全站儀不能夠從一個測站測出整個圓柱面，所以至少需要兩臺全站儀對其圓柱面進行觀測。然而，利用多臺全站儀測得的坐標點的數據不屬于同一套坐標系，為了使兩個測站上點的坐標統一，需要至少布設3個公共點在圓柱面的周圍。將全站儀分別架設在兩個不同的測站上觀測這些公共點，求得兩套坐標系之間的轉換參數，以便將兩套坐標系上的坐標點歸算到同一套坐標系中。為了提高坐標之間的轉換精度，布設的公共點之間的距離相對于圓柱面應盡量遠。

為了擬合蘇州市文廟大成殿某根圓柱形支柱，首先在支柱前后兩邊分別選擇一個點作為測站點，且在支柱周圍均勻地設定4個點，放置小棱鏡，作為坐標轉換的公共點。測得4個公共點坐標見表1。

表1 不同測站測得公共點坐標 m

1.2 三維坐標轉換

由于任意架設測站測得的公共點屬于不同的坐標系，為了便于圓柱面的擬合，需要進行三維坐標轉換，本文是將測站2的坐標歸算到測站1的坐標系中。由于這兩套坐標系又是全站儀任意確定的，因此該坐標轉換屬于大旋轉角的三維坐標轉換。文獻[3]中提出一種適合于大旋轉角的三維基準轉換的簡便模型，但是該方法相對于文獻[4]的方法列式和計算要復雜些，所以本文采用文獻[4]的方法，同樣可以進行大旋轉角的三維坐標轉換。

一般三維坐標轉換需要求解7個轉換參數，而在這里采用同一臺全站儀來獲取公共點的坐標，所以不必考慮尺度參數，只需要求出三個平移參數(x0,y0,h0)和三個角度參數(α,β,γ)就可以了。

公共點之間的坐標關系可以表示為：

(1)

其中，(x0,y0,h0)為平移量；α,β,γ均為旋轉角；R1(α)，R2(β)，R3(γ)均為旋轉矩陣，其中：

當公共點個數大于3個時，可以按最小二乘求解以上6個參數。對每個公共點，列出誤差方程為：

(2)

對式(2)進行線性化，得:

(3)

其中，偏導數和常數項見文獻[4]。

利用式(3)，經過平差處理后求解6個轉換參數，分別為x0=-199.800 1 m，y0=608.517 8 m，z0=97.907 1 m，α=-001′6.117 8″，β=003′5.667 4″，γ=-100016′38.840 7″。

將求得的6個轉換參數代入式(1)中，可將不同坐標系的點坐標歸算到相同坐標系，得到的圓柱面的坐標點的數據作為本文擬合圓柱面的實驗數據。

2 圓柱面擬合

根據圓柱面的幾何特征可知，圓柱面可以看做為到一條定向的中心軸線距離等于某一常數的點的集合，要想唯一確定一個圓柱，需要7個參數，分別是該圓柱中心軸線的方向向量(a,b,c)和直線上的某一點坐標(x0,y0,z0)，以及圓柱的半徑r。由此，可得該圓柱的中心軸線的參數式方程為：

(4)

其中，t為參數變量。

根據由二維平面圓擴展得到三維空間圓柱面的定義[1]，空間圓柱面的方程可以表示為:

(5)

其中，(x,y,z)為空間圓柱面上的點;(a,b,c)為單位向量。

將式(5)進行展開并進一步整理，得式(6):

(6)

則，誤差方程可列為：

V=r-R

(7)

由于誤差方程式(7)為非線性，需要對上式進行線性化。在線性化的過程中，由于上式各參數之間的相關性比較大，舍去了高次項對參數的計算結果影響比較大，而且需要對參數的初始值要求比較高，否則，可能導致迭代不收斂或者收斂到錯誤的結果。

為了在保證最優參數解的前提下，可任意選取平差過程中參數的初始值，因此對誤差方程進行相應的變換，并顧及條件a2+b2+c2=1。令誤差方程為:

v=r2-R2=T-R2=[a(zi-z0)-c(xi-x0)]2+[b(xi-x0)-a(yi-y0)]2+[c(yi-y0)-b(zi-z0)]2-R2

(8)

對式(8)進行線性化，得:

?vi=BX-L

(9)

X=(δx0,δy0,δz0,δa,δb,δc,δR)T;

其中，?./?.是對7個參數求偏導數；r0,R0均為代入參數近似值后的圓柱半徑。

由于x0,y0,z0這3個參數相關，a,b,c這3個參數也是相關的。為了保證參數結果的唯一性，需要對參數進行約束。又由于圓柱的中心軸線的確定需要指明方向和大小，為此規定中心軸線的方向向量是一個單位向量并指向正方向。即滿足條件a2+b2+c2=1，并規定a>0，若a=0，則b>0；若a=0且b=0，則c>0(a,b,c不能同時為0)。

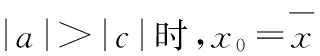
顧及兩個約束條件和式(9)的誤差方程，按附有約束條件的間接平差求解各參數的估值。然而，在每次迭代求解過程中，均需對a,b,c作單位化修正，以便收斂得到最佳的近似參數估值。

3 算例分析

本文是以無棱鏡全站儀測得蘇州市文廟大成殿某根圓柱形支柱的實際坐標數據為例，將測站2測的點位坐標利用式(1)全部轉換到測站1所在的坐標系中，然后按照本文提出的方法進行平差，求得確定圓柱面的7個參數。為了驗證這種方法的正確性，筆者采用文獻[1]和文獻[6]中圓柱擬合算法和數據進行驗算，將算得結果進行比較分析，如表2所示。

由表2可知，三種方法求得的圓柱中心軸線方向和半徑的結果十分接近。本方法與文獻[6]方法中初始值選取方法相同，都選取所有觀測點的x0坐標的平均值作為參數近似值，并將其設定為常數x0。本方法和文獻[1]方法的坐標平移量不同是由于選取的坐標初始值不同，為了進一步比較本方法和文獻[1]方法，可以將兩方法的初始值都設為x0=10.000 00，然后繼續按照上式進行平差計算，則起始點平移后的坐標為(10.000 00,20.384 86,4.035 87)，與文獻[1]中的計算結果相差很小，這就驗證了本方法的正確性。

表2 三種方法結果比較

從表2的結果可以看出本方法的正確性和可行性。所以，可以利用本方法來擬合測得的實際圓柱面坐標點的數據，求得圓柱的7個參數。同時，也利用文獻[6]中的方法擬合求得圓柱參數，并與本方法計算的結果進行比較分析，計算結果見表3。

表3 兩種不同方法的圓柱參數平差結果

由表3的圓柱的參數平差結果，可知這兩種方法都能用于圓柱面的擬合，而且求得的參數結果和精度結果相差不是很大，這也同時驗證了該方法的可行性。為了進一步說明該方法的有效性，利用本方法和文獻[6]方法求得圓柱面上點至圓柱中心軸線的距離與圓柱半徑之差[4]，即為圓柱的圓度，其計算結果見圖1。

由圖1可知，兩種方法計算的圓柱面的圓度值差異不大，驗證了該方法確實可以用于圓柱擬合的參數求解，且精度也符合要求。

4 結語

本文介紹了圓柱面擬合的一個快速簡便的方法，該方法是利用圓柱的幾何特征，列出空間圓柱面的方程，并顧及確定圓柱面參數之間的相關性，規定約束條件，再對誤差方程進行適當的變換，降低對參數近似值的要求，最終求出圓柱幾何參數的最佳近似估值。

通過本方法實例計算結果與文獻[1]和文獻[6]的方法比較分析，驗證了該方法的可行性。該方法與圓柱擬合的其他方法相比，形式簡單、易于理解、精度較高，是一種可以運用的圓柱面擬合方法。

[1] 潘國榮，谷 川.改進的遺傳算法用于工業測量數據處理[J].大地測量與地球動力學，2008,28(1)：55.

[2] 王麗華，谷 川，萬 軍.基于改進遺傳算法的雷達天線曲面擬合參數辨識[J].機電一體化，2008,14(4)：54.

[3] 陳 義，沈云中，劉大杰.適用于大旋轉角的三維基準轉換的一種簡便模型[J].武漢大學學報(信息科學版)，2004,29(12)：1101-1104.

[4] 王解先，季凱敏.工業測量擬合[M].北京：測繪出版社，2008:31-33.

[5] 秦世偉，潘國榮，谷 川，等.基于遺傳算法的三維空間柱面擬合[J].同濟大學學報(自然科學版)，2010,38(4)：604.

[6] 張益澤，王解先.初值任意選取的圓柱面擬合方法[J].工程勘察,2012(1):77-80.

Cylindersurfacefittinginarbitrarydirectionofspace

ChuJianchunZhangZefeng

(SuzhouSurveyingandMappingInstituteCo.,Ltd,Suzhou215000,China)

This paper presents a new simple and feasible cylinder surface fitting algorithm. The coordinates of the points on the cylinder surface are measured by the reflectorless total station and transformed into the same coordinate system. The geometric cylinder parameters can be determined by least squares method with arbitrary initial values and the circularity of each point is assessed at the same time. Compared with other methods, the results are similar and the accuracy is equal, which verifies the feasibility and correctness of the method.

cylinder surface fitting, 3D coordinates transformation, circularity, least squares method

1009-6825(2017)23-0190-03

2017-06-07

褚建春(1963- )，男，高級工程師; 張澤峰(1991- )，男，助理工程師

TU198

：A