基于拉普拉斯矩陣的K-mean聚類

王 超 潘正高 路紅梅 李雪竹

（宿州學院信息工程學院 安徽宿州 234000）

基于拉普拉斯矩陣的K-mean聚類

王 超 潘正高 路紅梅 李雪竹

（宿州學院信息工程學院 安徽宿州 234000）

譜聚類的方法被廣泛用在模式識別各個領域。文章運用K-mean聚類方法，主要闡述了如何由樣本的相似度矩陣構造的拉普拉斯矩陣來求解樣本的低維映射譜，根據低維映射譜進行譜聚類。

拉普拉斯矩陣；譜聚類；K-means

樣本聚類是無監督學習的一種重要分類方法。對于無標簽的樣本，要實現分類只能根據樣本本身的相似度進行分類，度量樣本相似度就是相似度聚類[1]。傳統聚類方法要知道樣本在N維空間的矢量[2]。但是拉普拉斯譜聚類的方法只需要知道樣本的相似度矩陣就能進行聚類。

一、圖譜理論到拉普拉斯矩陣

拉普拉斯矩陣式表示圖的一種矩陣，給定一個n個頂點的圖，則拉普拉斯矩陣被定義為：L=D-W

其中D為圖的度矩陣，W為圖的鄰接矩陣。

舉個例子，給定一個簡單圖，如下:

圖1 一個鄰接圖

把該圖轉化成鄰接矩陣的形式記為W則：

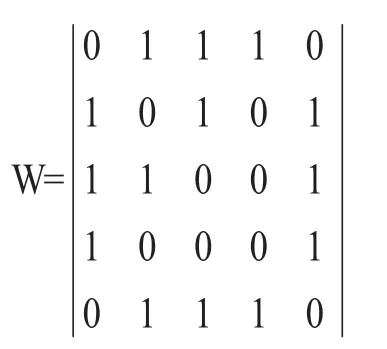
把W的每一列元素加起來得到n個數，然后把這個數放在對角線上其余位置都是零，組成一個n×n的對角矩陣，記為度矩陣D，如下所示：

根據拉普拉斯定義L=D-W可得拉普拉斯矩陣如下所示：

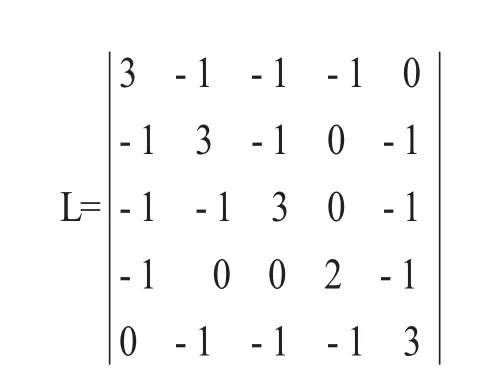
通過上面這個簡單例子，我們明白了拉普拉斯矩陣在連接圖上的定義。下面我們對于更一般的情況的數學描述如下：對于一個圖中定義A子圖和B子圖[3]，它們之間的所有邊的權值之和可以由鄰接矩陣W的一般形式求解如下：

其中，Wij定義為節點i到節點j的權值，如果兩個節點不相連，則權值為零。與某個節點i鄰接的所有邊的權值之和定義為該頂點i的度di，多個di形成一個度矩陣D。

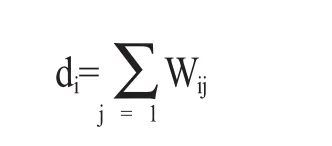
由以上定義可知拉普拉斯矩陣的性質如下：

（1）L是對稱半正定矩陣；

（2）L·1=0·1，即L的最小特征值是0，相應的特征向量是1；

（3）L有n個非負特征值0=λ1≤λ2≤…λn；

（4）對于任何一個實向量υ?Rn，有以下表達式成立：

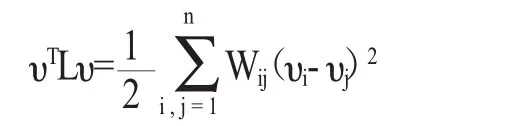
對性質（4）的證明如下：

二、聚類的圖譜解釋

聚類是把一堆樣本合理地分成兩份或份。從圖論的角度看，聚類問題就是圖的分割問題[4]。給定一個圖G=（V,M），頂點集表示各樣本，帶權的邊表示各樣本之間的相似度，譜聚類的目的是要找到一種合理的分割圖的方法，把圖分割為若干個子圖，使得連接不同子圖的邊的權重或者相似度盡可能的低，同一子圖內邊的權重或者相似度盡可能高。相似的聚集在一起，不相似的彼此遠離。為了達到這樣一個目的，就需要被切割的這些邊的權值之和最小[5]。

假設圖不相交的子圖分別為A1，A2，…，AK，求其代價最小的分割的目標函數如下：

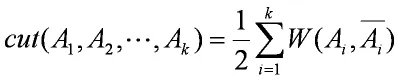
其中k表示分成了k個組，Ai表示第i組，Ai表示Ai的補集表示Ai,與Ai相連的所有邊之和。綜合上式就表示所有要切割的邊的權重之和。就是分割成個組要使得上式取最小值。這個目標函數在實際的操作中，常常把圖分割為一個點和其余n-1各點。為了讓每個圖都有合適的大小，上述的目標函數改寫成如下式子：

下面對這個目標函數進行推導：

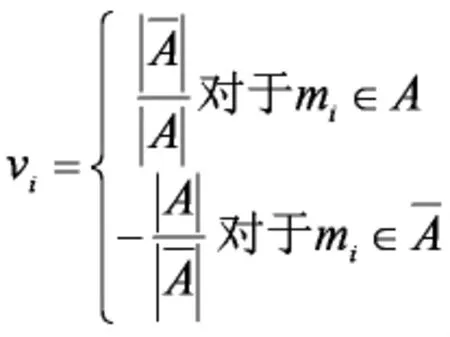
則上式可以化為：

我們從RatioCut推導出了vTLv，這也就是說拉普拉斯矩陣L和我們要優化的目標函數RatioCut有密切的聯系。因為是一個常量。最小化RatioCut，也就是最小化vTLv。

又因為：

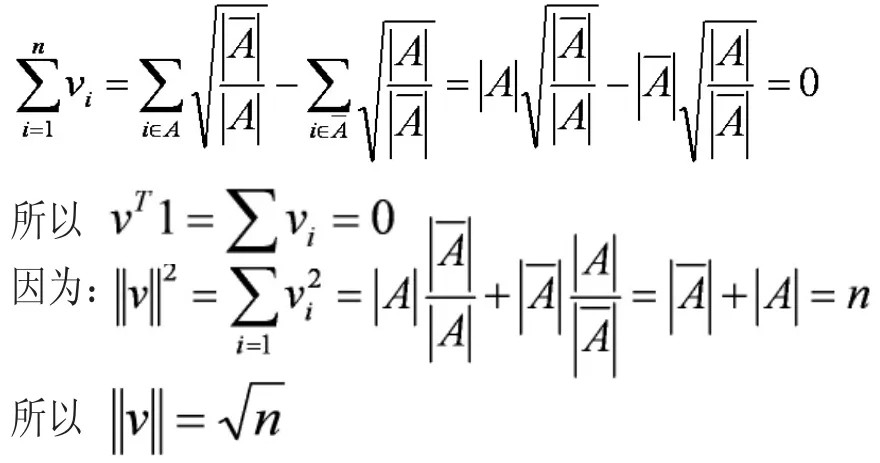
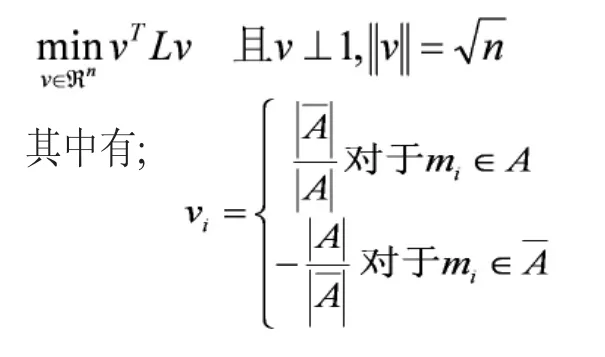
顯然上式n是一個定值，要最小化vTLv也就是最小化λ。因此我們下面只有找到拉普拉斯矩陣L最小特征值是零，對應的特征向量就行了。這里有一個問題，就是我們討論過的拉普拉斯矩陣最小特征值是零，對應的特征向量是1。不滿足v⊥1的條件了，這里根據文獻[2]所說理論。我們取第2小特征值對應特征向量。進一步，由于實際中的特征向量里的元素是連續的任意實數，所以可以根據v是大于0還是小于0對應到離散情況下的，決定vi是取還是取。而如果能求取v的前K個特征向量，進行K-means聚類，得到K個簇，便從二聚類擴展到了K聚類問題。而這里要求的K個特征向量就是拉普拉斯矩陣的特征向量。所以問題就轉換成了：求取拉普拉斯矩陣的前K特征值對應的特征向量，然后用這前K個特征值對應的特征向量進行K-means聚類。

三、K-means聚類

（一）隨機在圖中取K個點作為中心點。

（二）然后計算圖中所有點到K個中心點距離，假如P點離中心點S點最近，那么P點屬于S點群。

（三）分完群計算點群中心，用新的中心點作為點群中心點。

（四）重復步驟（2）和（3），直到中心點不再移動，聚類完畢。

四、結語

基于拉普拉斯矩陣的K-means聚類,一般步驟如下：

（一）根據數據構造一個圖，圖中每一個節點對應一個數據點，將各個數據點連接起來，并且邊的權重表示數據的相似度。把這個圖用鄰接矩陣W表示出來。

（二）把鄰接矩陣每一列元素加起來得到n個數，把它們放在對角線上，其他地方補零構成一個的對角陣，記為度矩陣D，并構造拉普拉斯矩陣L且L=D-W。

（三）求出拉普拉斯矩陣的前K個特征值對應的特征向量，特征值由小到大順序排列的。

（四）把這些特征向量（列向量）排列在一起組成一個nx·k的矩陣，將其中每一行看做k維空間的一個向量，并使用K-means算法進行聚類。聚類結果每一行所屬類別就是圖中節點也就是n個數據點分別所屬類別。

譜聚類算法和傳統聚類方法相比，譜聚類只需要數據之間的相似度矩陣就可以了，而不必想單純K-means聚類需要數據在N維歐式空間中的向量。

[1]H.Zha,C.Ding,M.Gu,X.He,and H.D.Simon.Spectral relaxationfor K-meansclustering[C].AdvancesinNeuralInformation ProcessingSystems14,Vancouver,Canada.Dec.2001:1057-1064.

[2]Fouss,F.,Pirotte,A.,Renders,J.-M.,and Saerens,M.. Random-walk computation of similar-ities between nodes of a graph with application to collaborative recommendation[J].IEEE Trans.Knowl.DataEng.[J].2007,19(3):355-369.

[3]Kannan,R.,Vempala,S.,andVetta,A..Onclusterings:Good, badandspectral.JournaloftheACM[J].2004,51(3):497-515.

[4]Hagen,L.andKahng,A.Newspectralmethodsforratiocut partitioning and clustering.IEEE Trans.Computer-Aided Design [J].1992,11(9):1074-1085.

[5]Gutman,I.andXiao,W.Generalizedinverse of the Laplacian matrixandsomeap plications[J].Bulletindel’Academie Serbedes Sciencesatdes Arts(Cl.Math.Natur.),2004,129:15-23.

[責任編輯 鄭麗娟]

TP391

A

2095-0438（2017）09-0153-03

2017-05-09

王超（1981-），男，安徽宿州人，宿州學院信息工程學院助教，碩士，研究方向：模式識別、人工智能、物聯網、圖像處理。

安徽省青年人才支持項目（gxfxzd2016256）；安徽省科技廳科技攻關項目（1502052053）。