基于流形學(xué)習(xí)的自適應(yīng)反饋聚類中心確定方法

李天龍+吳晟+吳興蛟+周海河+曹敏+王昕

引言

現(xiàn)如今，數(shù)據(jù)存在于我們生活的每一個(gè)角落，在大數(shù)據(jù)快速發(fā)展的今天，數(shù)據(jù)挖掘成了進(jìn)行數(shù)據(jù)分析的有效途徑，同時(shí)也是獲取數(shù)據(jù)信息的關(guān)鍵。

在海量數(shù)據(jù)下進(jìn)行研究要求對于數(shù)據(jù)規(guī)律的探索，數(shù)據(jù)的聚類就顯得尤為重要，目前對于聚類算法的研究大致歸納為五大類，分別基于分割、層次、密度、網(wǎng)格和模型。上述的許多聚類算法都在實(shí)際中得到了較好地運(yùn)用，同時(shí)也取得了一些效果，但是這些方法都存在一個(gè)共同的不足就是需要人工調(diào)參。這種方式將給自動化生產(chǎn)編程帶來一定限制。

正是由于存在上述問題，尋找一種能反饋調(diào)節(jié)聚類參數(shù)的算法就有其必要。

本文在對譜聚類算法進(jìn)行探究以后，提出一種基于目標(biāo)條件的反饋聚類。這種聚類方式對于大多數(shù)線性流形聚類參數(shù)選擇具有一定適應(yīng)性。

1相關(guān)理論

流形學(xué)習(xí)聚類隨著高維大數(shù)據(jù)問題被提出，經(jīng)過幾年的研究與探索，人們提出了大量的流形學(xué)習(xí)的理論與算法。比較典型的算法有ISOMAP、LLE、拉普拉斯算子特征映射（Laplacian eigenmaps）、最大方差展開（MVU）、局部切空間分析（LTSA）等。聚類，顧名思義就是根據(jù)樣本間相似度，將數(shù)據(jù)分成不同組。其中譜聚類是流形聚類中具有代表性的一種聚類方式。

譜聚類主要由以下四個(gè)步驟步組成：

Step1，構(gòu)建相似度矩陣，即計(jì)算每個(gè)數(shù)據(jù)點(diǎn)與其余數(shù)據(jù)點(diǎn)的相關(guān)系數(shù)。

Step2，計(jì)算拉普拉斯矩陣，并將其進(jìn)行歸一化；

Step3，生成最大的k個(gè)特征值和對應(yīng)的特征向量；

Step4，采用k-means方法對特征向量進(jìn)行聚類。

2模型建立

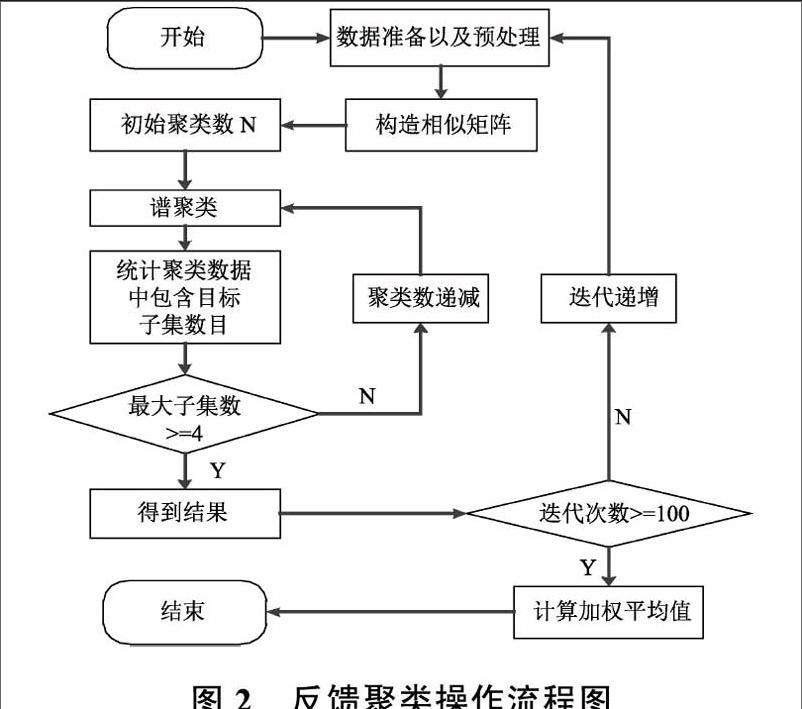
提出的反饋聚類算法主要基于譜聚類實(shí)現(xiàn)，聚類數(shù)目首先隨意指定，在一次聚類結(jié)束后將聚類結(jié)果代入目標(biāo)中驗(yàn)證，如果未達(dá)到目標(biāo)閾值則調(diào)整聚類數(shù)，進(jìn)行新的聚類，直到所得聚類結(jié)果滿足聚類目標(biāo)。得到結(jié)果后經(jīng)過多次迭代后計(jì)算聚類數(shù)的加權(quán)平均以后得到的聚類數(shù)。反饋聚類流程圖如圖1。

2.1數(shù)據(jù)集設(shè)置

譜聚類的前提是構(gòu)造相似矩陣，這就要求將不同構(gòu)型或者不同維數(shù)的數(shù)據(jù)進(jìn)行處理。一般根據(jù)特征值或者矩陣實(shí)際運(yùn)用得到新的n階方陣。

2.2構(gòu)造相似度矩陣

基于譜聚類的方法是建立在譜圖理論基礎(chǔ)上，其基本思想是將樣本看作頂點(diǎn)，樣本間的相似度看作帶權(quán)的邊，從而將聚類問題轉(zhuǎn)為圖分割問題，即找到一種圖分割的方法使得連接不同組的邊的權(quán)重盡可能低，組內(nèi)的邊的權(quán)重盡可能高。與傳統(tǒng)的聚類算法相比，其具有能在任意形狀的樣本空間上聚類且收斂于全局最優(yōu)解的優(yōu)點(diǎn)。可根據(jù)公式1構(gòu)造聚類相似矩陣。

2.3反饋?zhàn)V聚類

建立如下譜聚類模型：

Step1：輸入一個(gè)MN的矩陣w，即w中一共包含N個(gè)數(shù)據(jù)點(diǎn)；

Step5：計(jì)算矩陣L的歸一化矩陣E的k個(gè)最大特征值及對應(yīng)的特征向量，形成一個(gè)N K的特征矩陣，記為Q；

Step6：對特征矩陣Q做k-means聚類，得到一個(gè)N維向量c，c中分別對應(yīng)相似度矩陣w中每一行所代表的對象的所屬類別，即最終的聚類結(jié)果。

Step7：驗(yàn)證聚類結(jié)果包含目標(biāo)最大子集數(shù)是否大于閾值，大于閾值則得到結(jié)果，否則調(diào)整聚類數(shù)執(zhí)行Step6。

Step8：多次迭代算法得到聚類列表ListC。

2.4計(jì)算加權(quán)平均

得到列表ListC以后，針對列表中的數(shù)求加權(quán)平均數(shù)成為新的聚類數(shù)。如公式5。

3實(shí)例驗(yàn)證

3.1數(shù)據(jù)集設(shè)置

實(shí)驗(yàn)數(shù)據(jù)取自2016年研究生數(shù)學(xué)建模B題數(shù)據(jù)。

先從數(shù)據(jù)清洗，缺失值處理以及數(shù)據(jù)變換方面進(jìn)行預(yù)處理。

數(shù)據(jù)清洗，主要通過數(shù)據(jù)統(tǒng)計(jì)查看有無存在ATCG四種堿基以外的其他構(gòu)成。尋找到除了ATCG以外，數(shù)據(jù)還存在I和D，后來根據(jù)官方文件修正為T和C。

缺失值處理，使用函數(shù)查看數(shù)據(jù)有無空值，最后發(fā)現(xiàn)無缺失現(xiàn)象。不必進(jìn)行插值以及增補(bǔ)。

數(shù)據(jù)變換，由于數(shù)據(jù)直接使用ATCG字符難以計(jì)算距離，所以對其進(jìn)行編碼形成編碼文件。

首先將文件gene info導(dǎo)入后根據(jù)每一條基因?qū)?yīng)的位點(diǎn)構(gòu)建合適的堿基對矩陣，構(gòu)建相似矩陣。

附件gene info文件夾中有300個(gè)dat文件。每個(gè)dat文件數(shù)據(jù)表示每個(gè)基因的位點(diǎn)信息，每個(gè)dat文件表示一個(gè)基因。和附件文件genotype.dat中的位點(diǎn)信息相結(jié)合進(jìn)行數(shù)據(jù)挖掘和分析。附件所給出的數(shù)據(jù)格式不能滿足數(shù)據(jù)挖掘的要求，所以進(jìn)行數(shù)據(jù)預(yù)處理。

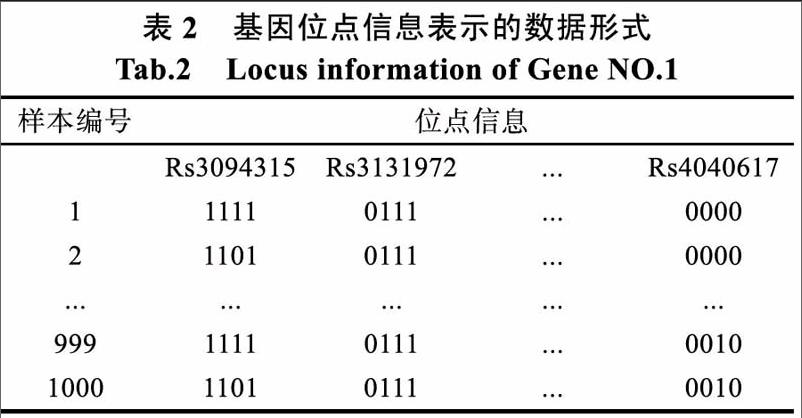
將附件給出的300個(gè)文件合并導(dǎo)入EXCEL文件中，并對基因從上到下依次編號。局部結(jié)果如表1所示。

數(shù)據(jù)的初級預(yù)處理得到如表2所示的數(shù)據(jù)格式，表的第一列為300個(gè)基因編號，其余列為基因的位點(diǎn)信息。由于基因含的位點(diǎn)數(shù)目不同，所以在基因信息和位點(diǎn)信息合并時(shí)需要對缺省基因進(jìn)行補(bǔ)缺省值得處理，采用補(bǔ)0。把基因位點(diǎn)對應(yīng)表和genotype.dat導(dǎo)入MATLAB進(jìn)行數(shù)據(jù)的第二步數(shù)據(jù)預(yù)處理，把兩個(gè)數(shù)據(jù)相互融合。以編號為l的基因?yàn)槔诤虾蟮玫饺绫硭镜臄?shù)據(jù)形式。

300個(gè)基因的數(shù)據(jù)格式如基因1位點(diǎn)信息格式。經(jīng)過兩步數(shù)據(jù)的預(yù)處理，數(shù)據(jù)的各項(xiàng)要求滿足數(shù)據(jù)挖掘的信息。

3.2模型求解

硬件環(huán)境：2.6 GHz CPU，8G內(nèi)存。

軟件環(huán)境：Windows7，matlabR201 3a。

根據(jù)反饋聚類操作流程，如圖2，在1000"9446高維矩陣下，設(shè)定參數(shù)最大子集閾值為4，迭代次數(shù)為100。使用MATLAB實(shí)現(xiàn)流行聚類算法，本文采用譜聚類方法對數(shù)據(jù)進(jìn)行100次聚類分析，每次聚類會產(chǎn)生一種聚類分組，從基因組中選取滿足致病基因覆蓋點(diǎn)大于等于4的基因組作為候選組。執(zhí)行完成算法后會產(chǎn)生100組候選數(shù)據(jù)。使用統(tǒng)計(jì)學(xué)方法統(tǒng)計(jì)100個(gè)候選組基因出現(xiàn)次數(shù)最多的基因。并計(jì)算中位數(shù)以及加權(quán)平均數(shù)描繪其實(shí)時(shí)曲線，進(jìn)行對照。

4實(shí)驗(yàn)結(jié)果與分析

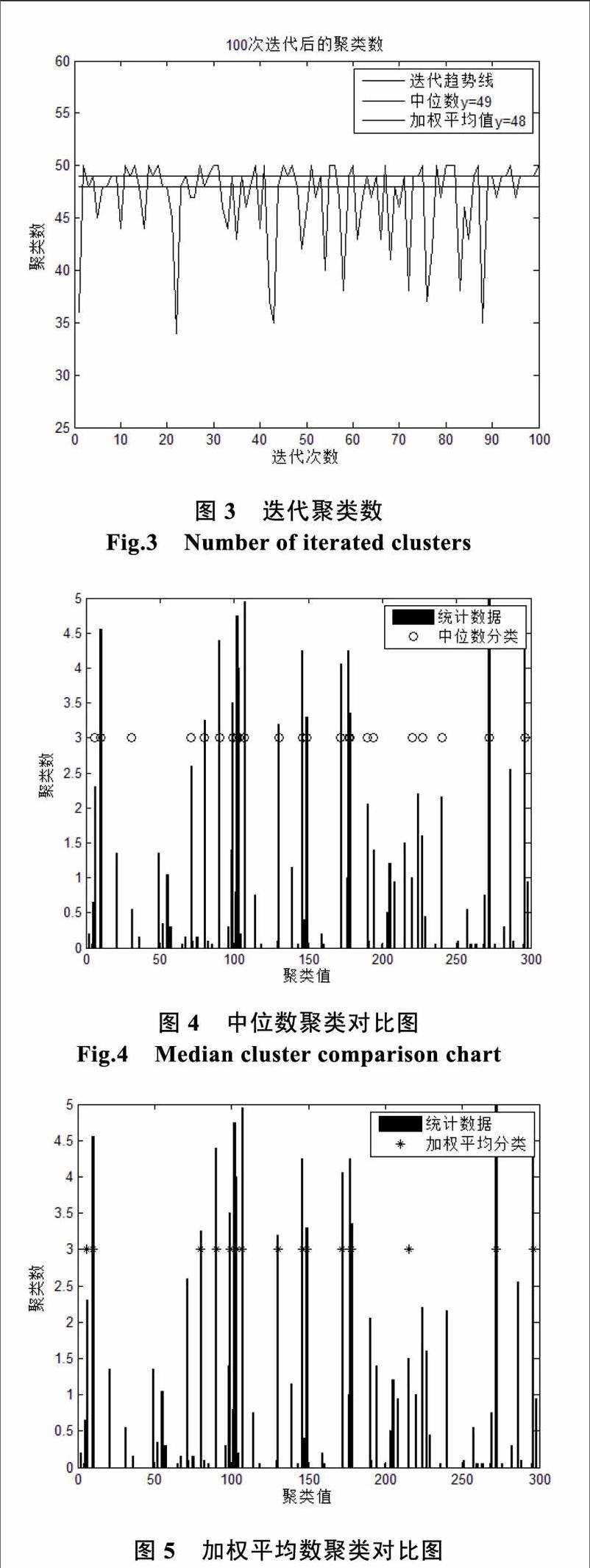
迭代一百次以后，統(tǒng)計(jì)聚類次數(shù)，得到各次聚類曲線圖，分別計(jì)算聚類集合中位數(shù)以及聚類集合加權(quán)平均數(shù)，如圖3所示。

觀察曲線可以初步得知加權(quán)平均數(shù)更能體現(xiàn)統(tǒng)計(jì)規(guī)律。

分別將得到的中位數(shù)以及加權(quán)平均數(shù)進(jìn)行聚類。得到聚類后數(shù)據(jù)與統(tǒng)計(jì)數(shù)據(jù)對比，對比圖4，圖5中包含統(tǒng)計(jì)值的數(shù)量。

最后對比得出，使用加權(quán)平均分類數(shù)得到的聚類集合更能體現(xiàn)統(tǒng)計(jì)數(shù)據(jù)。

5結(jié)論

通過反饋?zhàn)V聚類方法迭代后的中位數(shù)以及加權(quán)平均數(shù)來確定聚類數(shù)，改善了流形聚類中聚類數(shù)難以確定的難題，通過不斷的適應(yīng)目標(biāo)從而調(diào)整聚類數(shù)，然后再通過不斷迭代后的加權(quán)平均數(shù)來得到最后的聚類值。再和得到的中位數(shù)進(jìn)行聚類效果的比較，這種方式下得到的結(jié)果是：使用加權(quán)平均數(shù)獲得的聚類數(shù)更加鍥合要求。endprint