GM—AR模型在城市地面沉降預測中的應用

張玲霞 趙曉光 曹慶東

【摘要】隨著城市的現代化進程，地面沉降已廣泛發生在世界各地，給人民生活和社會發展造成極大損失。GM（1，1）模型作為經典的地面沉降預測方法得到了廣泛應用，不適用于隨機型數據預測。將AR模型與GM（1，1）組合成GM-AR模型對城市地面沉降數據進行預測，預測值殘差小于GM（1，1）模型，未來2、3期預測值小于1mm，且趨勢線更貼近實測值，效果優于傳統的GM（1，1）模型。

【關鍵詞】灰色模型；自回歸模型；城市地面沉降

Application of GM - AR Model in Urban Ground Subsidence Prediction

Zhang Ling-xia1，Zhao Xiao-guang2，Cao Qing-dong1

（1.Shandong Yellow River Survey and Design InstituteJinanShandong250000；

2.Shandong Yellow River Information CenterJinanShandong250000）

【Abstract】With the modernization of the city， land subsidence has been widespread in the world， to the people's lives and social development caused great losses. GM （1，1） model has been widely used as a classical ground subsidence prediction method， and it is not suitable for stochastic data prediction. The AR model and GM （1，1） are combined into the GM-AR model to predict the urban ground subsidence data. The predicted residual value is less than GM （1，1） model， the predicted value of the next two is less than 1mm， and the trend line More close to the measured value， the effect is better than the traditional GM （1，1） model.

【Key words】Gray model；Autoregressive model；Urban land subsidence

1. 引言

（1）地面沉降是在自然和人為因素作用下，由于地表松散土體壓縮而導致區域性地面標高降低的一種環境地質現象[1]，人類的生存活動如地下水資源、礦產資源的開采，高層建筑物的建造等，都會破壞原有的土層結構，打破地殼上部的受力平衡，使地表塌陷或凸起造成土壤變形。隨著工業的發展和人口的增長，工業用水及居民生活用水量大大增加，資源的消耗量持續上升，高層建筑群的數量也逐年增加，致地面沉降廣泛發生于世界各地，給人民生活和社會發展造成極大損失，今年來隨著城市建設的逐步開展，隨之也給地質帶來了影響，為了保證城市建設的順利進行，有必要對城市地面的變化進行監測和未來變化進行預測。

（2）采用數學模型進行逼近、模擬、揭示變形特性從而進行地面沉降預測成為近年來研究的熱點，常用的數學預測模型有GM（1，1）模型（灰色模型）、Kalman濾波、人工神經網絡模型、時間序列分析等預測模型，以上模型具有自己的使用條件和優缺點，采用不同的預測模型可以得到不同的預測結果。在數學預測模型中GM（1，1）模型（灰色模型）適用于分析具有確定性趨勢的數據[2]，現已被廣泛應用[3]；AR模型（Auto Regressive，自回歸模型）采用的是隨機過程中自身歷史值的線性組合來描述整個過程[4]，該方法能夠適用于分析平穩的隨機監測數據[2]，但是由于城市地面沉降受到多種因素的影響，但大致可分為確定性部分和隨機性部分，因此，本文將采用兩種模型進行組合的方式GM-AR組合模型對城市地面沉降數據進行分析預測，并與只采用GM（1，1）模型（灰色模型）的預測結果對比，分析GM-AR組合模型的應用效果。

2. AR模型原理

AR模型設時間序列觀測值為為y0，y1 ，…yn ，模型為P階，序列中其余元素與前 P個元素可組成關系[5][6]如式（1）

y ^ p+1=yp1 +yp-12+…+y1p+Δp+1

y ^ p+2=yp+11 +yp2+…+y2p+Δp+2

……

y ^ n=yn-11 +yn-22+…+yn-pp+Δn

（1）

式中， y ^ i 為預報值，1，2，…，p 為參數， Δi為觀測誤差，共有 n-p個方程

則AR（P） 模型的預報方程為式（2）

y ^ =∑n i=P+1 yi ^ i-p （2）

3. GM-AR組合模型

3.1灰色模型GM（m，n）的基礎概念是灰色模塊，核心模擬建模方法是微分擬合法，其中模型參數m是模型微分方程的階數，n是參與建模的序列個數，在建模時微分方程階數越大，計算就復雜，但是精度的提高則不明顯，因此本文中就采用m=1，n=1時的模型GM（1，1）作為預測模型，令非等間隔時間序列觀測值x0， x1，…，xn，然后通過內插得到等間隔時間序列建立GM（1，1）模型，建立過程如下：

3.2對 x0（t）進行1次累加得到遞增序列 x1（t）=x1（1），x1（2），…，x1（n）通過1階灰色模塊構成一階線性微分方程 dx（1）dt+ax1=b，其中a是用以控制系統發展態勢的大小稱之為發展系數，b用來反應資料數據之間變化的關系，稱之為灰色作用量；通過原始數據序列構成大于2的方程組，令Y=XB+E其中E為誤差項，Y，B為：endprint

Y= x0（2） x0（3） x0（n） ，B= ab （3）

3.3根據最小二乘原理得到最小二乘解：B=（XTX） -1（XTY） =[ab]T，把a，b值帶回原方程得

x（1）t= x0（t）-ba e-at + ba （4）

3.4求出其殘差序列y0， y1，…，yn， 對殘差序列建立AR模型，則利用GM-AR組合模型對沉降量的預測結果可寫為： x（t） = x0（t）-ba e-at + ba

+∑yi ^ i-p

（5）

式中，前一項為GM（1，1）模型部分，后一項為AR（p）模型部分。

4. 實例分析

4.1采用某地二等水準測量沉降觀測數據，應用GM（1，1）模型與GM-AR模型對比分析，取AR模型階數P=4 ，預測結果及殘差見表1。

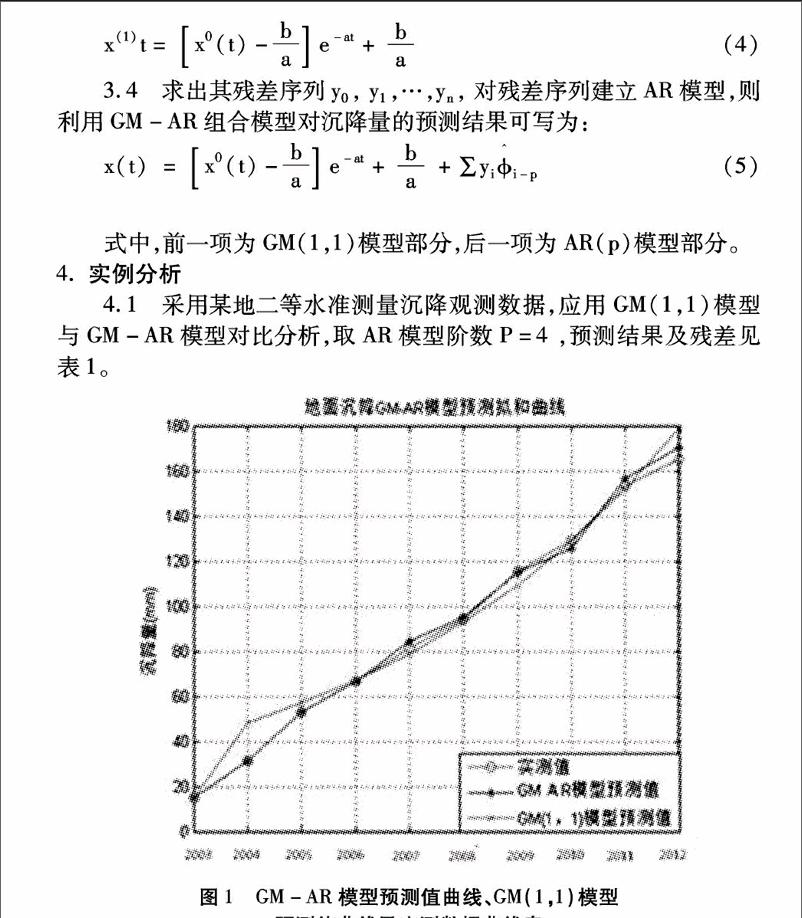
4.2為方便直觀的表現模型效果，現將實驗中的GM-AR模型預測值曲線、GM（1，1）模型預測值曲線及實測數據繪制成圖，效果如圖1所示：

4.3由表1可以看出，GM（1，1）模型雖能對沉降量做出預測，但殘差很大，在預測第3期數據時殘差絕對值已出現大于5mm的情況，在預測第6期數據時殘差絕對值已大于10mm；GM-AR模型，預測值殘差較小，在預測第6期數據時殘差絕對值等于5mm，前5期均小于5mm，未來第2、3期數據的預測值殘差絕對值在1mm之內。由圖1可知，GM-AR模型預測值曲線、GM（1，1）模型預測值曲線及實測數據走勢大致相同，但GM-AR模型預測值曲線走勢更接近于實測數據，從圖像未來發展趨勢看，GM（1，1）模型曲線在未來第6期數據以后已偏離了實測數據，而GM-AR模型預測值曲線依然與實測數據走勢相同，且更接近于實測數據。

5. 結論與展望

（1）GM（1，1）模型、GM-AR模型都是預測地面沉降的有效方法。GM（1，1）模型對確定性趨勢的數據預測效果較好，AR模型適合分析隨機性數據。本文將上述兩種模型結合，在使用GM（1，1）模型對地面沉降觀測值的確定性部分預測后，使用AR模型對其預測殘差再進行擬合，補充GM（1，1）模型對于沉降數據隨機性部分預測的缺失，從而達到對地面沉降的精確預測，且GM-AR模型形式簡單、參數較少，滿足城市地面沉降等相關工程的建模、預報需求。

（2）隨著城市的發展，對于城市地面沉陷理論的研究也在逐步深入，預測模型之間的組合預測驗證也將會得到進一步的研究，同事模型預測的精度需要大量數據的驗證，所以未來對于沉陷數據的采集將會更加智能化和集中化，高效便捷的采集數據手段都已出現如三維掃描技術等。

參考文獻

[1]鄭銑鑫，沿海地區城市發展與地面沉降的系統控制[J]，海洋地質與第四紀地質，1992，（1）：57～65.

[2]高寧，崔希民，高彩云.灰時序GM-AR模型在建筑物沉降變形預測中的應用[J].測繪科學，2013，38（1）：139～141.

[3]王有良，唐躍剛.曲線擬合與GM（1，1）模型沉降預測及相關性分析[J].測繪科學，2008，（3）：98～99，78.

[4]金瑤，蔡之華.基于AR模型的Kalman濾波在股票價格預測中的應用[J].統計與決策，2013，（6）：80～82.

[5]焉建國， 陳正松， 羅志才， 等. 基于 AR 模型的上海地區地面沉降預測分析[J]. 大地測量與地球動力學， 2009， 28（5）： 121～124.

[6]蘭孝奇，楊永平，黃慶，嚴紅萍.建筑物沉降的時間序列分析與預報[J].河海大學學報（自然科學版），2006，34（4）：426～429.

[7]曾山，徐兮.基于AR模型的填方路基沉降檢評方法[J].重慶交通大學學報（自然科學版），2013.endprint