“薄透鏡焦距測定”實驗的教學(xué)探討
方光宇,辛 麗,趙海發(fā)
(哈爾濱工業(yè)大學(xué) 物理實驗中心,黑龍江 哈爾濱 150001)

“薄透鏡焦距測定”實驗的教學(xué)探討
方光宇,辛 麗,趙海發(fā)
(哈爾濱工業(yè)大學(xué) 物理實驗中心,黑龍江 哈爾濱 150001)
討論了薄透鏡焦距測量實驗中的一些基本問題和主要的系統(tǒng)誤差來源,針對教學(xué)中容易產(chǎn)生問題的實驗現(xiàn)象給出了重點分析. 利用目鏡分劃板系統(tǒng)代替?zhèn)鹘y(tǒng)像屏能準確確定像平面位置,并以此為基礎(chǔ)設(shè)計了綜合性實驗.
薄透鏡;焦距;像平面
幾何光學(xué)實驗是光學(xué)基礎(chǔ)實驗, 實驗?zāi)康牟粏渭兪桥浜侠碚撜n的學(xué)習(xí),更重要的是讓學(xué)生通過實驗加深對光學(xué)基本概念和成像規(guī)律的理解,進而掌握基于幾何光學(xué)的光學(xué)儀器如顯微鏡、望遠鏡、焦距儀、分光計、經(jīng)緯儀等儀器的工作原理和使用方法,并通過實驗培養(yǎng)學(xué)生解決實際問題的能力和嚴謹?shù)目茖W(xué)態(tài)度.
幾何光學(xué)實驗中,“薄透鏡焦距的測定”實驗是最為基礎(chǔ)的光學(xué)實驗[1]. 因為學(xué)生在中學(xué)學(xué)過薄透鏡的成像規(guī)律和高斯公式,很多學(xué)生覺得實驗原理簡單,導(dǎo)致對該實驗不夠重視,但實際上不少學(xué)生對幾何光學(xué)有些錯誤認識和不正確的理解,導(dǎo)致先入為主達不到實驗教學(xué)效果. 本文以該實驗為例,介紹教師在指導(dǎo)實驗時有針對性地對學(xué)生存在的問題所采取的教學(xué)要求和加深認識的解決辦法.
1 實驗原理
對于單透鏡的成像規(guī)律,學(xué)生應(yīng)該熟練掌握高斯公式,即

(1)
對于凸透鏡和凹透鏡高斯公式在形式上完全一樣,只是在計算時凸透鏡焦距取正值,凹透鏡焦距取負值. 對于物距和像距,中學(xué)物理中已經(jīng)學(xué)習(xí)實像和虛像,分別對應(yīng)了大于0和小于0的像距v. 而對于物,則只討論了實物的成像規(guī)律,即u>0的情形. 實際上,u也可推廣到實數(shù)范圍. 大學(xué)物理中物的概念被擴展到虛物,即物距不僅僅可以是大于0的實數(shù),還能取小于0的值,它對應(yīng)虛物的概念. 這樣,物距和像距都可取任意實數(shù),對應(yīng)的像的性質(zhì)也可根據(jù)像距的符號直接判斷出來. 表1~2總結(jié)了凸透鏡和凹透鏡對于實數(shù)物距u的成像規(guī)律.

表1 凸透鏡(f>0)成像規(guī)律

表2 凹透鏡(f<0)成像規(guī)律
從表1~2中可以看出,光軸上物距為0,f,2f, ±∞ 的4個物點對應(yīng)像點的像距v分別為0,±∞,2f,f. 這4對共軛點在薄透鏡成像規(guī)律中有重要的應(yīng)用:u=0為薄透鏡的光心,共軛點為自身;u=f為焦點,共軛點為無窮遠點,可以利用放在焦點的發(fā)光物以產(chǎn)生平行光. 反之,根據(jù)光路可逆物距u=±∞對應(yīng)了平行光,通過透鏡后相聚v=f,即會聚在焦點. 望遠鏡聚焦到無窮遠處后,目鏡系統(tǒng)的分劃板就位于物鏡的焦平面上;2倍焦距點u=2f對應(yīng)像距v=2f,放大率為1.
在薄透鏡成像基本原理的分析中,應(yīng)重點讓學(xué)生注意虛物的概念,因為本實驗中測量凹透鏡焦距的自準法和物距-像距法都要利用虛物成像. 另外要強調(diào):幾何光學(xué)成像的要點是物點和像點是一一對應(yīng)關(guān)系,這是與全息成像不同之處;再者要明確焦平面的1個物點對應(yīng)著像方的某個方向的平行光,而且不同物點對應(yīng)的平行光方向不同,這是學(xué)生容易出現(xiàn)的錯誤.
在光路分析中,薄透鏡軸外物點成像作圖法應(yīng)要求學(xué)生掌握3條光線及其共軛光線的作法: 通過光心的光線、平行于光軸的光線、通過物方焦點的光線.
2 實驗內(nèi)容和操作要點
2.1光路調(diào)節(jié)
實驗之前, 首先要對光具座上各光學(xué)元件進行調(diào)節(jié),使各元件的光心處于同一直線上, 稱為“共軸”. 另外實驗過程中,物、像和透鏡的位置、移動距離等都是沿主光軸計算,而測量則是通過光具座的導(dǎo)軌進行的,因此還要求主光軸和導(dǎo)軌平行,即各元件的光心相對于導(dǎo)軌位于同一高度,稱為“等高”.
單個凸透鏡和對稱發(fā)光物的等高共軸調(diào)節(jié)常用兩次成像,調(diào)節(jié)透鏡高低,使大像、小像中心重合的辦法. 也可以按圖1所示, 先移動物屏和發(fā)光物靠近, 在物屏上標(biāo)出發(fā)光物中心P的高度P′,適當(dāng)拉開物屏和像屏的距離,放入凸透鏡,調(diào)節(jié)凸透鏡高度,使像中心和P′重合.

圖1 光具座上各元件的等高共軸調(diào)節(jié)
多個透鏡等高共軸調(diào)節(jié)則在調(diào)好單個透鏡后依次加入下一個透鏡,調(diào)節(jié)新加入透鏡的高度, 使成像的中心和原中心重合即可.
2.2凸透鏡焦距測量
2.2.1 自準法
自準法光路緊湊,操作簡單,成像清晰,位置容易判斷,可以直接測量焦距而不需要復(fù)雜的計算, 比其他使用像屏的方法更準確判斷成像清晰位置. 自準法在光學(xué)儀器的調(diào)節(jié)如分光計調(diào)節(jié)中, 也有直接的應(yīng)用. 當(dāng)望遠鏡物鏡和分劃板距離調(diào)節(jié)到等于一倍焦距之后,發(fā)光綠十字和它通過平面反射鏡所成的像位于同一個平面即分劃板上,望遠鏡就聚焦到了無窮遠處.
在講解自準法時,應(yīng)要求學(xué)生能熟練畫出光路圖. 光路調(diào)至自準后,發(fā)光物和凸透鏡即構(gòu)成準直管. 物上每一點發(fā)出來的光通過凸透鏡后都是平行光,但這并不意味著準直管發(fā)出來的光是無擴散的,它有一定的角度范圍.
在自準法實驗操作時還應(yīng)注意區(qū)分干擾像和自準像. 干擾像指的是當(dāng)物屏和透鏡不滿足自準條件時在物屏上出現(xiàn)的像. 如果實驗使用的是平凸透鏡,則凸面正對物屏?xí)r依然可以準確測量透鏡的焦距. 因為此時反光面可以看成是平面反射鏡, 見圖2(a). 而當(dāng)透鏡的凸面背對物屏?xí)r存在干擾像,此時反光面等效于凹面反射鏡,在物屏和透鏡距離小于焦距時出現(xiàn),見圖2(b). 這個距離與透鏡表面曲率半徑及透鏡材料的折射率有關(guān).

(a)

(b)圖2 平凸透鏡自準法測量焦距光路圖
自準法原理中容易讓人忽略的問題是:除了上述透鏡自身的反射成像外,是否還有其他位置也能在物屏上得到清晰的像? 這是可能的,即當(dāng)平面反射鏡剛好位于像面時,如圖3所示. 然而此時很難在物屏上觀察到反射回來的像,因為根據(jù)光路可逆原理,此時反射回來在物屏上成的像是正立等大的,即使旋轉(zhuǎn)反射鏡,也基本上和原來的物重合,難以區(qū)分. 所以在這種情形下一般不會給實驗者造成干擾. 而自準像和透鏡表面反射的干擾像是倒立等大的,物和像正好組成一個圓圈,很容易發(fā)現(xiàn).

圖3 平面鏡位于像平面時在物屏上的像和物重合
自準法測量焦距主要系統(tǒng)誤差來源于透鏡主面位置的測量. 實驗中使用的是對稱雙凸透鏡,因此物方焦距和像方焦距相等,但由于透鏡厚度并不為零,不但主面和中心面位置有偏離,實驗時光具座上的中心線也不一定正對透鏡的中心面,都給實驗帶來誤差. 主面和中心面位置的偏差是薄透鏡近似所固有的,無法消除. 而中心面和光具座中心線不重合則可通過將物放在透鏡右側(cè)平面鏡方左側(cè)再次測量,取2次測量平均值而消除.
2.2.2 位移法

圖4 位移法測量凸透鏡焦距
位移法要求物屏—像屏距離A>4f,否則無法在物屏上得到實像. 球差是位移法測量凸透鏡焦距的主要誤差來源. 因為理想薄透鏡焦距是對于近軸光線成像而言,如果成像光束角度較大(如圖5所示),近軸光線成像點P′較遠,遠軸光線成像點P″較近. 此時對于實驗者來說,最清晰像的位置在P′和P″之間. 位移法中第一次成大像,如果利用最清晰成像位置作為透鏡位置,則u1偏小, 第二次成小像,最清晰成像位置u2偏大. 這樣,l=u2-u1的值比實際值偏大,導(dǎo)致焦距測量值偏小. 因此,實驗中如果利用較清晰而不是最清晰成像位置來計算,可以減小球差帶來的系統(tǒng)誤差[3].
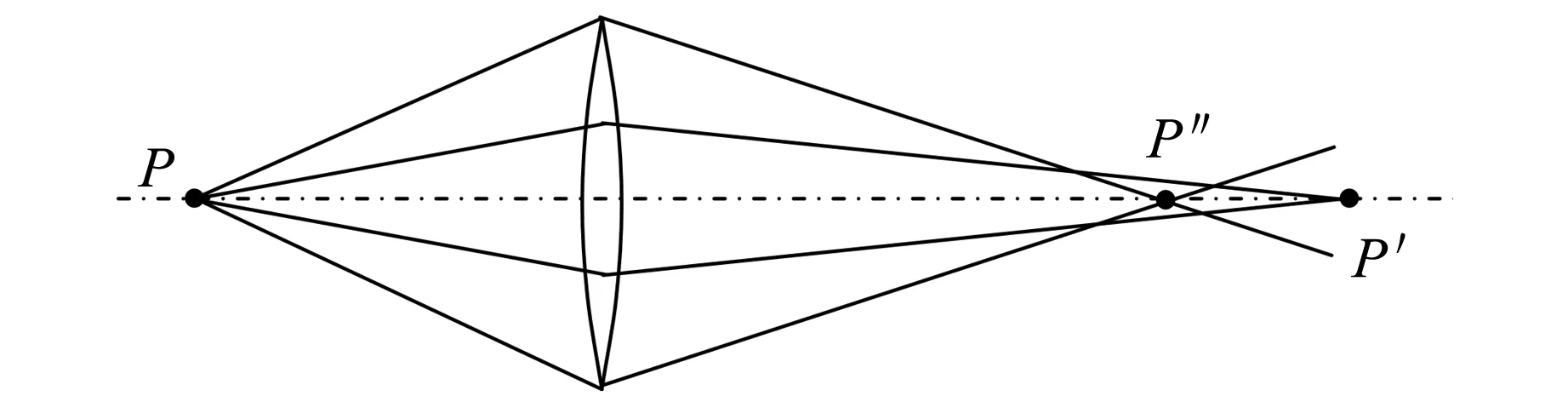
圖5 球差導(dǎo)致位移測量產(chǎn)生系統(tǒng)誤差
2.3凹透鏡焦距測量
2.3.1 自準法
自準法凹透鏡焦距測量原理和凸透鏡類似. 因凹透鏡對實物不能成實像,需利用輔助凸透鏡的實像作為凹透鏡的虛物,當(dāng)凹透鏡離虛物等于焦距時, 通過平面鏡反射在物屏上得到自準像.

干擾像的存在也提供了一種測量透鏡材料折射率的方法,據(jù)此可以為學(xué)生提供的設(shè)計性實驗題目: 測量薄透鏡玻璃材料的折射率.
生產(chǎn)中常用1∶30公雞與母雞比例開展蛋種雞人工授精。本實驗擬探討經(jīng)對種公雞優(yōu)種培育,提升優(yōu)質(zhì)種公雞質(zhì)量后,公雞與母雞比例達到1∶80時的種蛋受精率情況。
2.3.2 物距-像距法
凹透鏡物距-像距法直接利用成像公式通過測量物距和像距計算焦距. 和自準法一樣, 也要利用輔助凸透鏡產(chǎn)生一個虛物.
物距-像距法誤差的主要來源除了上述的主面位置誤差、球差之外,還有清晰成像位置的測量誤差. 以凸透鏡成像為例,如圖6所示,P為軸上物點,通過凸透鏡的理想像點為P′,像屏置于此處即可獲得最清晰的像,偏離這個位置像變得不清晰,屏上得到的是圓形的彌散光斑,稱為彌散圓. 由于人眼的分辨角不是無限小,只要彌散圓的張角不超過人眼的最小分辨角δ,人眼就不能區(qū)分像點和彌散圓,此時在實驗者看來,成像的清晰度不變. 在光照充足的條件下,人眼的最小分辨角αe=1′,而實際分辨角還要更大一些. 當(dāng)人眼觀察明視距離25 cm處的物體時,最小的分辨距離取δ=0.15 mm[3-4],即使不是理想成像,只要像點的彌散圓直徑不超過δ,人眼就不能區(qū)分. 按照這個標(biāo)準,圖6中,像屏在P′左右2Δx范圍中移動,實驗者都會認為成像是清晰的,這個范圍即為焦深.

圖6 凸透鏡成像的幾何焦深
實驗中,所使用的凸透鏡焦距f=200 mm,孔徑D=30 mm. 簡單計算表明,人眼觀察像屏利用清晰度調(diào)焦至少給焦距帶來10 mm的極限誤差. 考慮到物理焦深等其他誤差,最后得到焦距的誤差會更大. 因此實驗操作中,若不考慮球差,可以通過移動像屏,找到成像清晰的區(qū)間, 取區(qū)間的中點作為清晰像的位置,能減小焦深帶來的誤差.
3 實驗拓展——利用目鏡系統(tǒng)的消視差調(diào)焦
以上是傳統(tǒng)的薄透鏡焦距測量實驗內(nèi)容,可以看出,無論是自準法、位移法、還是物距-像距法,最大的誤差來源于調(diào)焦誤差. 為了比較精確地確定像的位置,在教學(xué)中采用了目鏡+分劃板構(gòu)成的目鏡系統(tǒng)[2],利用它代替像屏或物屏,通過消視差確定調(diào)焦后透鏡或像的位置.
如圖7所示,在自準法測量凸透鏡焦距時,先調(diào)節(jié)目鏡至分劃板的距離,使眼睛能清楚舒適地看清分劃板的叉絲. 眼睛通過目鏡觀察像和叉絲同樣清晰,再橫向改變視角觀察兩者有無視差,把縱向調(diào)焦變成橫向?qū)剩?jīng)過消視差而定焦. 理論證明:采用合適的目鏡系統(tǒng),這種綜合調(diào)焦的精度要遠高于單純靠像屏上成像清晰度判斷的調(diào)焦精度. 學(xué)生通過本實驗中消視差操作的訓(xùn)練之后,能夠更好地理解和使用一些精密光學(xué)測量儀器,如顯微鏡、望遠鏡、焦距儀、移測顯微鏡、分光計、經(jīng)緯儀、橢偏儀、瑞利干涉儀等.

圖7 自準法中利用目鏡系統(tǒng)消視差調(diào)焦測定透鏡焦距
在學(xué)生掌握了目鏡系統(tǒng)的調(diào)焦及其在測量中使用后,提出了一個設(shè)計性實驗,要求學(xué)生測量雙凹薄透鏡材料的折射率. 提供元件:光具座、凸透鏡3個(焦距均未知,需要學(xué)生選擇正確的透鏡作為目鏡和凹透鏡輔助成像的凸透鏡)、待測凹透鏡1個(焦距未知)、分劃板1個、平面反射鏡1個、大頭針1枚、橡皮泥少許、臺燈1盞.
雙凹透鏡2個表面都為球面,其兩球面半徑分別為R1和R2,且透鏡為中央厚度遠小于2個球形表面半徑的薄透鏡. 透鏡材料折射率為n,空氣折射率取為1. 對于傍軸光線,雙凹薄透鏡的焦距f滿足磨鏡者公式
(2)
要利用式(2)計算折射率,必須先要測量出凹透鏡的焦距以及前后2個球面的半徑. 焦距的測量可以利用自準法,而表面曲率半徑的測量要利用球面的反射成像基本規(guī)律,即物和像在光軸同一位置時,物距或像距就等于球面的半徑.
因為沒有提供像屏,要準確測量凹透鏡的自準成像和表面反射成像的位置,需要制作目鏡系統(tǒng),通過清晰度法和消視差法調(diào)焦確定成像位置. 為了調(diào)焦時光線充足,需要用臺燈照亮分劃板上的大頭針.
首先制作目鏡系統(tǒng):選擇適當(dāng)焦距的凸透鏡L0作為目鏡,用大頭針AB、橡皮泥和空鏡架制作叉絲. 然后用自準法測量凹透鏡焦距,光路如圖8所示. 利用已知焦距透鏡L1對叉絲成像,測量物距u,計算出像距,從而確定成像位置A′B′. 放入凹透鏡和平面鏡,使得通過目鏡能看到叉絲AB及其清晰倒立的成像A″B″,并移動凹透鏡消除視差,則凹透鏡L2到A′B′的距離即為|f2|.

圖8 自準法測量凹透鏡焦距
測量凹透鏡表面曲率半徑光路如圖9所示,去掉平面鏡和凸透鏡L1,利用凹透鏡的前表面反射成像A1B1,消視差后到凹透鏡的距離即為表面曲率半徑R1. 同樣方法測出后表面曲率半徑R2.

圖9 測量凹透鏡表面曲率半徑光路圖
最后將測得的凹透鏡焦距f2、曲率半徑R1和R2代入(2) 式,得出透鏡材料的折射率.
這個實驗綜合了凹面鏡反射成像、薄透鏡成像等幾何光學(xué)中的基本知識,還訓(xùn)練了學(xué)生使用目鏡系統(tǒng)進行調(diào)焦和測量,加深了對光學(xué)知識的理解,對培養(yǎng)學(xué)生的創(chuàng)新能力有較好的作用, 類似的方法也可用來測量薄凸透鏡材料的折射率.
4 結(jié)束語
本文討論了薄透鏡焦距測量實驗中的一些基本問題和主要的系統(tǒng)誤差來源, 建議利用目鏡分劃板代替?zhèn)鹘y(tǒng)像屏以準確確定像平面位置,并以此為基礎(chǔ)設(shè)計了綜合性較強的實驗,在教學(xué)中取得良好的效果.
[1] 趙海發(fā),辛麗,方光宇,等. 大學(xué)物理實驗[M]. 北京:高等教育出版社,2015.
[2] 金恩培,周素瓊,張立彬,等. 傳統(tǒng)幾何光學(xué)教學(xué)實驗裝置的改進[J]. 物理實驗,2003,23(12): 38-39.
[3] 馬興坤. 物象互換法測凸透鏡焦距的誤差分析[J]. 物理實驗,1989,9(6):258-260.
[4] 黃志平,陳志華,馮卓宏,等. 凹透鏡焦距測量中的景深和誤差分析[J]. 實驗室研究與探索,2013,32(10):21-24.
[5] 蘇大圖. 光學(xué)測試技術(shù)[J]. 北京:北京理工大學(xué)出版社,1996.
[責(zé)任編輯:尹冬梅]
Discussionontheexperimentofmeasuringthefocallengthofthinlens
FANG Guang-yu, XIN Li, ZHAO Hai-fa
(Teaching Center of Physics Experiments, Harbin Institute of Technology, Harbin 150001, China)
Some basic problems in the experiment of focal length measurement of thin lens was discussed, the main sources of systematic errors and the experimental phenomena that confused the students were analyzed. In this experiment, the eyepiece reticle system was used instead of the traditional image screen to confirm the image plane. Based on this, a comprehensive experiment was designed.
thin lens; focal length; image plane
2017-07-22
黑龍江省高等學(xué)校教改工程項目(No.JG2014010690)
方光宇(1973-),男,湖南岳陽人,哈爾濱工業(yè)大學(xué)物理系副教授,博士,從事大學(xué)物理實驗教學(xué)與研究工作.
O435.2
:A
:1005-4642(2017)09-0030-05

