基于元胞傳輸模型的過飽和交叉口信號控制方法

陽杰，王吉棟

(西南交通大學 交通運輸與物流學院，四川 成都 610031)

基于元胞傳輸模型的過飽和交叉口信號控制方法

陽杰，王吉棟

(西南交通大學 交通運輸與物流學院，四川 成都 610031)

為克服現有交叉口信號控制優化方法在實際應用中的局限性，利用二維元胞傳輸模型構建交叉口信號的元胞傳輸模型。以交叉口飽和度的函數作為通行能力權重，綜合考慮交叉口各進口的交通狀態，并對過飽和進口引入飽和度的罰函數，實現對過飽和進口的優先優化；最后利用遺傳算法進行交叉口信號控制的動態優化求解。實例驗證表明：所構建的模型同時適用于過飽和及非飽和交叉口的信號控制優化，并可有效降低過飽和進口道及交叉口整體的飽和度，有助于提升交叉口的整體通行效益。

信號控制優化；元胞傳輸模型；飽和度；通行能力；遺傳算法

隨著城市機動車保有量的持續增長，城市交通擁堵日益嚴重。交叉口作為城市交通網絡的關鍵節點，其通行能力直接影響整個路網的通行效益，在早晚高峰時段交叉口的交通流經常處于過飽和狀態，導致交叉口排隊累積和排隊溢出，嚴重影響區域通行能力。由于大部分交叉口道路空間資源有限，因此，主要通過對交叉口信號的控制優化提升其整體通行效益。

目前，常用的交叉口信號配時方法有Webster、Akcelik、HCM、TRRL算法和沖突點法等；但這些方法主要適用于交叉口的低飽和情況，均以交叉口延誤最小化為優化目標，未考慮過飽和狀態。文獻[1]利用線性規劃法構建適用于各種交通狀態的單點交叉口的信號配時優化模型，并利用實際交叉口驗證優化模型的有效性。文獻[2]提出考慮整個過飽和時段的信號相序決策方法，構建離散動態優化模型，確定最佳周期時長和最佳相位綠燈時長，表明所提出的離散型性能指標模型更合適于過飽和信號相序的優化。文獻[3]針對過飽和交叉口構建離散動態優化模型，驗證該模型較連續動態優化模型控制效果更佳。文獻[4]以信號相位為離散變量構建過飽和狀態下的單交叉口離散優化模型，并結合極小值原理給出最佳信號周期與各相位最佳綠信比優化求解算法。文獻[5]利用光滑連續函數替代常用的階躍函數逼近累積到達和離開曲線，構建以擁堵時段駛出車輛數最大化為目標的動態線性規劃模型，算例驗證該方法的總延誤優于TRANSYT-7F模型。文獻[6]以信號周期為決策變量，以交叉口整體車輛延誤最小、排隊車輛最少為目標函數，構建交叉口的周期時長優化模型，并驗證周期時長與到達率、延誤、停車率等指標間的灰關聯性。文獻[7]以交叉口的平均延誤、停車次數和通行能力為目標函數，并結合交叉口整體飽和度為多目標組合權重，利用遺傳算法對優化模型進行求解。文獻[8]以交叉口各進口道排隊率作為飽和度的權重，以交叉口各進口道綜合飽和度最優為目標，構建適用于單點交叉口信號控制的優化模型。

目前部分優化方法只適用于非飽和交叉口，而針對過飽和交叉口的優化主要集中在交叉口的整體效益指標，如交叉口整體通行能力、延誤、停車率、最大排隊長度等，而未針對關鍵進口進行突出優化，同時未充分考慮各進口道的交通擁堵程度[9]。本文構建一種適用于交叉口過飽和狀態，綜合考慮各進口道擁堵程度和關鍵車流的信號控制優化模型，以期能夠解決過飽和交叉口的信號控制優化問題。

1 構建基于CTM的交叉口模型

1.1 CTM基本原理

Daganzo在1993年提出了元胞傳輸模型(CTM模型)[10-11]，該模型是對宏觀交通流理論(LWR)的離散近似，能覆蓋流量-密度-速度基本關系的整個范圍；可很好地描述交通流的演化過程，如干擾和排隊的形成、波動、消散以及擁擠波的逆向傳播等重要的交通行為；能夠反映交通動力學特征，適應車流的動態變化，可很好地適用于擁堵或非擁堵狀態的交通流防真[12]。

在CTM模型中，假設路段上的交通流量q和密度k滿足

q=min{vfk,Q,u(kjam-k)} ，

式中：kjam為交通流的擁擠密度；Q為路段上的最大交通流量；vf為自由流速度；u為擁擠波傳播速度。

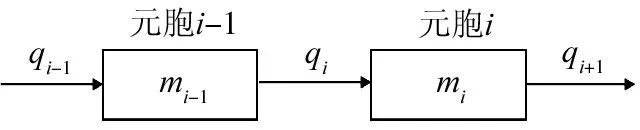
圖1 CTM中元胞流量傳輸示意圖

CTM模型中將路段劃分為多個均勻長度的元胞，如圖1所示，圖1中i為元胞編號，qi為元胞i在第t個仿真時間步長內實際輸入的交通流量，mi為元胞i在第t個仿真時間步長內的車輛數。

同時將時間離散為相等的時間步長Δt，元胞長度lc等于標準車輛在自由流狀態下行駛一個仿真時間步長的距離，即

lc=vfΔt，

(1)

元胞之間流量傳輸如圖1所示，根據元胞流量守恒，元胞狀態(包括車輛數、輸入輸出流量等參數)隨時間更新的關系滿足

mi′=mi+qi-qi+1,

式中mi′為t+1時段元胞i內的車輛數。

t時段元胞i-1流入元胞i的車流量qi滿足

qi=min(Ri，Si)，

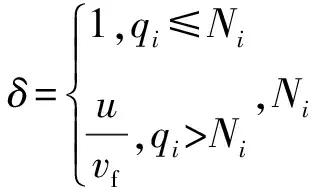
1.2基于CTM的交叉口模型構建

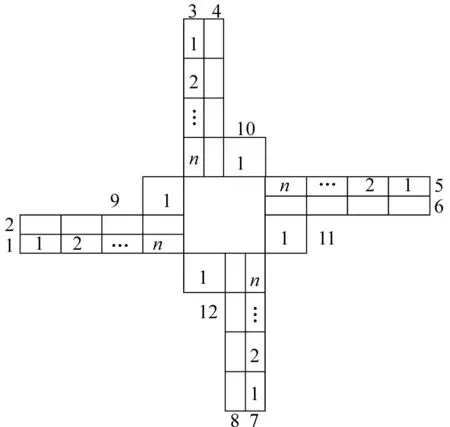
圖2 基于CTM的交叉口模型

由于實際信號控制中， 右轉車流不受交叉口信號控制，因此，構建交叉口CTM模型時不考慮右轉車道。基于二維元胞傳輸模型，構建交叉口的元胞傳輸模型如圖2所示，將進口道直行、左轉車道化為2條進口流鏈，匝道及其銜接的地面車道被單獨劃分為1條交通流鏈[13-14]。4個進口有第1～8共8條流鏈。將交叉口出口單獨化為1條流鏈，4個出口有第9～12共4條流鏈。元胞(j，n)表示位于流鏈j的第n個元胞。

每條進口流鏈的第一個元胞(j,n)均相當于一個大型的停車場，所有等待進入路段的車輛均停放在該元胞中；第一個元胞的輸出流量q(j,1)即為交叉口各進口的外部動態交通需求。

每條進口流鏈的最后一個元胞(j，n)用于實現交叉口信號控制的效果，當t時刻進口流鏈j所屬相位為綠燈時，元胞(j，n)的發送流量則為進口道的飽和流量；當t時刻為紅燈時，元胞(j，n)的發送流量為0。

元胞(j，n)發送的流量

出口鏈只包含1個元胞，其容量為無窮大；所有離開交叉口的車輛均駛入該元胞。

2 構建交叉口信號控制動態優化模型

在進行交叉口信號控制優化時，常用的評價指標主要有延誤、排隊長度、停車率、通行能力和行人過街的等候時間等[15-16]。從交通參與者的角度出發，應使車流通過交叉口的延誤盡可能小；從道路資源利用效率的角度出發，應使交叉口的通行能力盡可能大。

2.1交叉口效益指標分析

1)排隊長度

在元胞傳輸模型中，可以通過統計各流鏈各相位綠燈開始時刻元胞中的車輛數得出排隊車輛數，從交叉口各進口道停車線開始向上游檢測各條流鏈阻塞的元胞，所有阻塞元胞內的車輛數總和即為該流鏈的排隊長度。交叉口各進口道距上游交叉口的距離Lj即為交叉口各進口道允許的最大排隊長度，各進口道的排隊長度應滿足最大排隊長度約束:

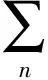
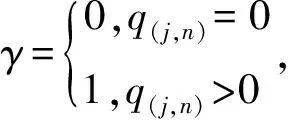
2)通行能力、飽和度

CTM模型中各進口鏈尾段元胞在綠燈期間按其飽和流率(單位有效綠燈時間內所通過的最大流量)釋放所能通過的最大流量則為通行能力；飽和度即為實際流量與通行能力之比，當飽和度大于1時，交叉口處于過飽和狀態，飽和度小于1時，交叉口處于非飽和狀態。

設Yjx為交叉口各條進口流鏈的車道飽和度，即第x周期內進入各進口流鏈的總交通量與各進口流鏈通行能力之比，反映了交叉口的擁擠程度。初始周期內進入匝道和各進口的總交通量可通過匝道及交叉口的元胞狀態變量統計得出，即初始周期開始時刻t0交叉口各進口道內的車輛數與一個周期時長T0內進入各進口道的車輛數的總和。有

(2)

(3)

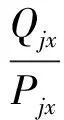
(4)

Yx=max(Yjx)，

(5)

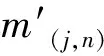
2.2信號控制動態優化模型

采用加權延誤總和最小化作為目標函數[17-18]；對各進口的延誤乘以飽和度函數進行放大，以體現各進口不同飽和度對綠燈時長的需求和不同配時方案下通行能力的差異；同時對過飽和進口的通行能力乘以指數權值放大，有利于對過飽和進口進行突出優化。有

(6)

s.t.

tmin≤tpx≤tmax,p=1,2,3,4,

lj≤Lj,j∈{1,2,3,4,5,6,7,8},

式中：Px為第x周期加權通行能力；tpx為第x周期相位p的綠燈時長；Tx為周期時長，Tmin≤Tx≤Tmax；φ為進口道飽和度的罰函數，用于突出優化過飽和進口道；gpx為相位綠燈時長，s；p為信號相位序號,p=1，2，3，4分別表示東西進口直行、左轉，南北進口直行、左轉。

相位綠燈應滿足最小綠燈時間和最大綠燈時間約束，信號周期也應滿足最小周期時長和最大周期時長限制。交叉口排隊長度應滿足路段長度約束，尤其是對過飽和交叉口，有利于防止排隊溢出。

3 基于遺傳算法的多目標信號控制模型求解

遺傳算法(Genetic Algorithm，GA)是模擬自然界生物遺傳和進化機制而建立起來的一種搜索優化算法，體現“優勝劣汰、適者生存”的競爭機制，具有很強的全局搜索能力。遺傳算法將問題域的可行解集合作為一個群體，群體中各個體分別對應一個可行解，在求解優化過程中將生物的適者生存規則和個體間的隨機信息交換機制相結合，模擬生物界進化的過程，采用人工干預的方式對可行解空間進行隨機優化搜索。

遺傳算法的遺傳操作包含選擇、交叉、變異；遺傳算法的核心內容主要為參數編碼、初始群體的設定、適應度函數的設計、遺傳操作設計、控制參數設定等。

本文選取最常用的二進制編碼進行信號控制優化問題的可行解編碼[19-20]。在信號控制優化過程中的決策變量為各相位綠燈持續時間t1、t2、t3、t4，例如用[aM/4…a1，bM/4…b1，cM/4…c1，dM/4…d1]代表一個染色體(染色體中的某一部分aM/4…a1等表示遺傳算法中一個綠燈持續時間t1的二進制的編碼段，一個二進制的編碼101011對應著一個十進制的數)，則染色體中的各部分[aM/4…a1]、[bM/4…b1]、[cM/4…c1]、[dM/4…d1]分別與各相位的綠燈時間t1、t2、t3、t4對應。本文采用目標函數作為遺傳算法的適應度函數，利用輪盤賭進行種群個體選擇，使用兩點交叉的方法進行種群個體的交叉重組，當迭代過程達到預先設定的代數K時，終止迭代。

4 實例驗證

以成都市某交叉口為例，對本文構建的信號控制優化算法的有效性進行驗證。各條進口道包含左轉、直行、右轉車道各1條，結合圖2中CTM模型構建方法建立該交叉口元胞傳輸模型。根據實際調查，取各進口道路段長度L=450 m，自由流速度vf=36 km/h，仿真時間步長Δt=3 s，由式(1)得元胞長度lc=30 m，將路段劃分為15個元胞，參數設定如表1所示。

交叉口為四相位信號控制，信號周期為120 s， 其中第一相位(東西進口直行)綠燈37 s，第二相位(東西進口左轉)綠燈25 s,第三相位(南北進口直行)綠燈29 s，第四相位(南北進口左轉)綠燈17 s。對該交叉口工作日晚高峰17：30—18：30時段交通量調查結果如表2所示；CTM模型中各步長的外部交通需求采用均勻輸入。

表1 交叉口元胞傳輸模型參數

表2 各進口元胞傳輸模型流量參數 pcu/h

根據綠信比(一個信號相位的有效綠燈時長與周期總時長之比)和飽和流率(一條進口車道在一次連續的綠燈時間內，能夠連續通過停車線的折算為小轎車的最大車輛數，pcu/h)計算得知，交叉口西進口的直行車道飽和度為1.11，處于過飽和狀態；南進口直行車道飽和度為0.79，處于非飽和狀態，選取這2條車道進行分析。HCM手冊中信號優化初始化時間選取為15 min，利用MATLAB構建交叉口的元胞傳輸模型，按初始配時運行8個周期初始化路網交通狀態。初始時段(0～900 s,即第1～8周期)內，過飽和及非飽和進口道的車道占有量和累計排隊長度如圖3、4所示，圖3、4中元胞16為進口鏈下游出口，停車線位于第16個元胞起點，排隊車輛從停車線開始依次第1個元胞方向排隊。

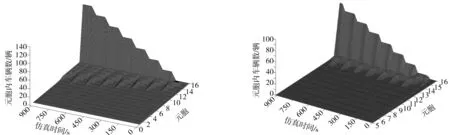
圖3 西進口直行車道交通量占有量 圖4 南進口直行車道交通量占有量

圖3反映了西進口直行車道的排隊長度形成、消散過程以及排隊滯留現象。圖3水平面內8個山丘形長度分別對應第1～8周期的排隊最大長度。隨著仿真時間逐步增長，排隊滯留車輛隨時間逐漸累積，第1周期排隊末尾處于第12個元胞，到第7周期排隊長度已延伸至第6個元胞,由此可知該進口處于過飽和狀態。圖4反映了南進口直行車道的排隊長度形成、消散過程。圖4水平面內8個山丘形狀長度始終保持不變，說明第1～8周期排隊長度均能完全消散，該進口處于非飽和狀態。

從圖3、4分析可知，本文所構建的交叉口元胞傳輸模型，能模擬出過飽和、非飽和狀態的交通波形成與消散過程。

利用式(2)～(4)獲得CTM模型中各進口交通效益指標，結合式(6)構建多目標信號控制優化模型。設定遺傳算法中染色體長度為30，最大迭代代數為100，交叉率為0.9，變異率為0.05，種群規模為40。初始化時段為0～900 s(第1～8周期)，優化時段為900～2 700 s，選取第9～15周期進行優化前后效果對比分析。優化前，交叉口采用的固定信號配時，每一周期長度均為120 s(除去12 s黃燈時間，則綠燈時間為108 s)，利用遺傳算法求得各優化周期的信號配時(有效綠燈時長)如表3所示。

優化前后西進口直行、左轉車道排隊長度l1、l2對比分析如圖5、6所示。西進口直行車道在0～900 s排隊車輛不斷累積，l1持續增長，最長達450 m；進行動態優化后，900～2 700 s西進口直行車道排隊長度逐步下降，并維持在100 m以內。西進口左轉交通需求較小，l2均維持在3 m以內，每周期排隊車輛均能完全消散。

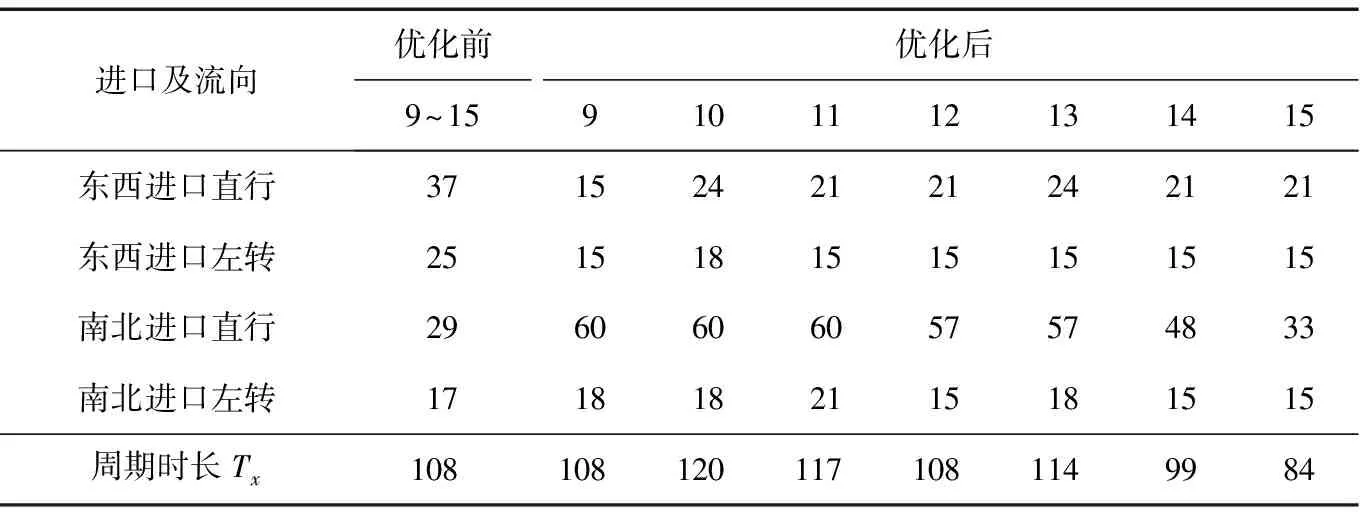
表3 交叉口各優化周期優化前后的信號配時 s

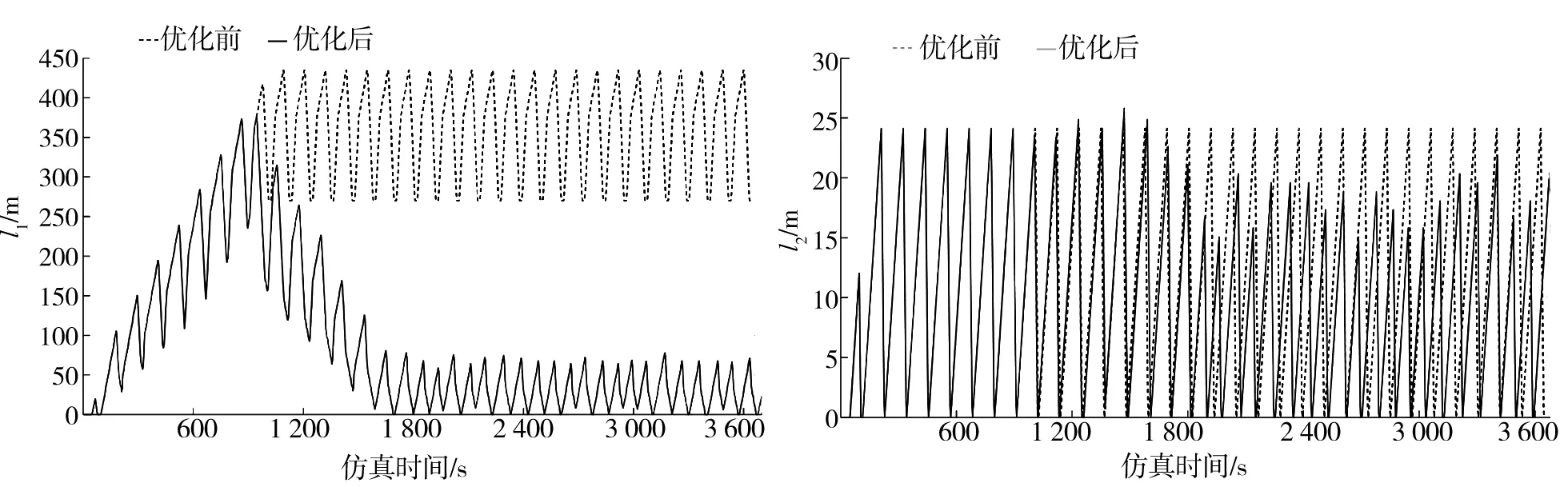
圖5 西進口直行車道排隊長度對比 圖6 西進口左轉車道排隊長度對比

圖7、8為優化前后北進口直行、左轉車道排隊長度l3、l4對比。北進口由于受信號周期波動的影響，導致l3、l4短時間內增長；優化時段后期。l3、l4趨于穩定，并小于優化前的排隊長度。

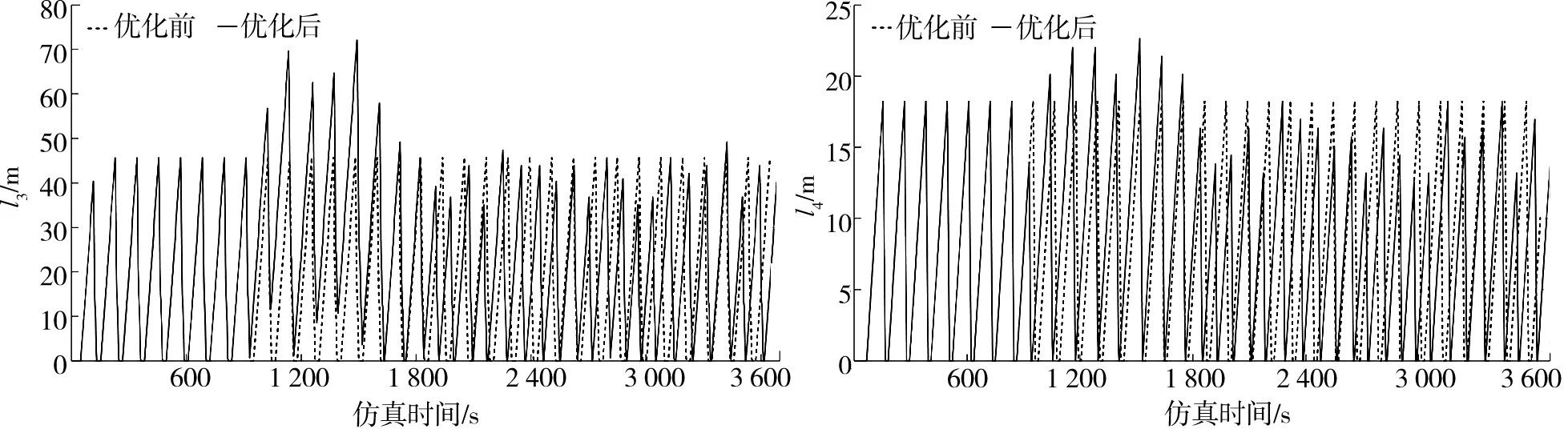
圖7 北進口直行車道排隊長度對比 圖8 北進口左轉車道排隊長度對比

結合表3所得每周期各相位綠燈時長gpx和表1中各車道的飽和流率S(j,n)，由式(4)～(5)計算第9～15周期優化前后交叉口整體及各進口飽和度如表4所示。優化后交叉口整體飽和度以及過飽和進口道飽和度顯著下降，交叉口通行效率顯著提升。

5 結論

基于二維元胞傳輸模型構建交叉口的元胞傳輸模型，并以交叉口飽和度的函數為權重，充分考慮各進口的交通狀態，以各進口加權通行能力總和為目標函數，突出對過飽和進口的優先優化。通過實例分析，文中所構建的交叉口元胞傳輸模型可準確的模擬交通流的轉播，包括排隊的形成與消散過程，同時，利用本文所構建的動態優化模型，可有效降低過飽和進口道和交叉口整體的飽和度，提升交叉口的整體通行效益。

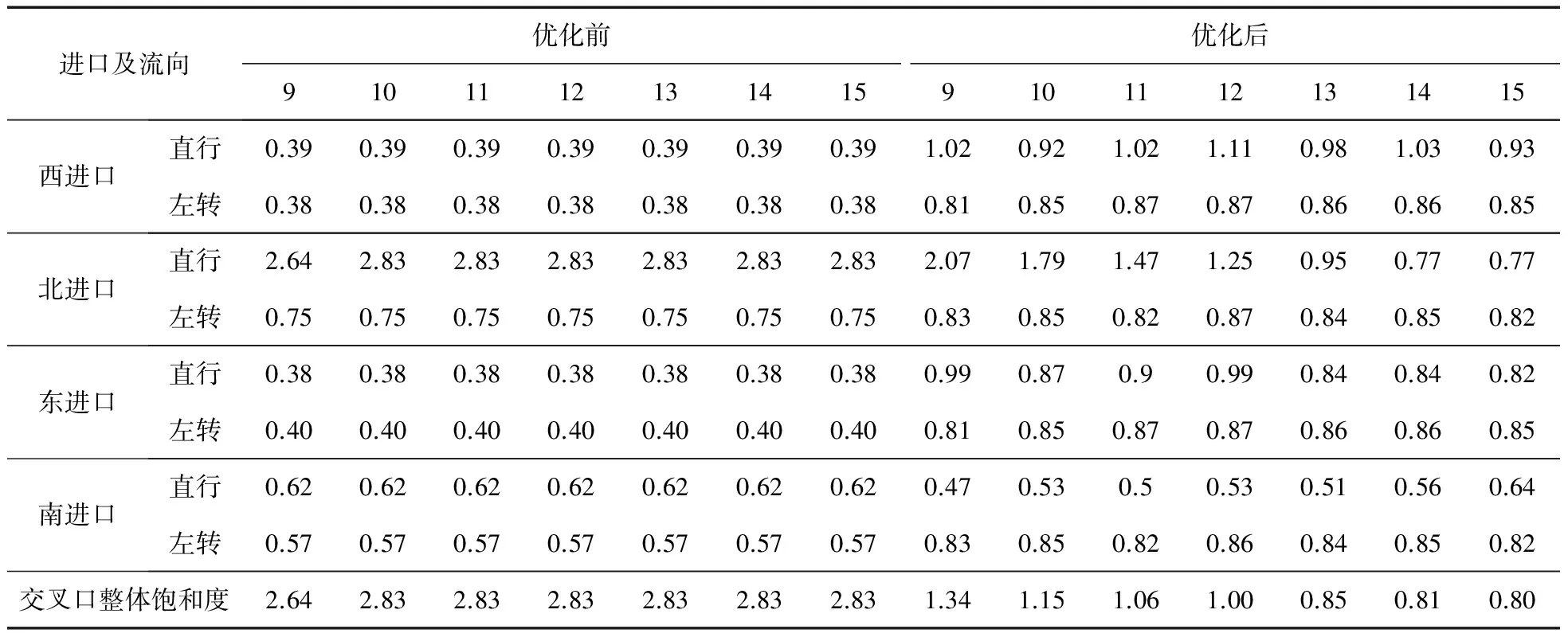
表4 交叉口各進口車道第9～15周期優化前后飽和度對比分析

[1]CEDER A,RESHETNIK I.An algorithm to minimize queues at signalized intersections[J].Journal of the Operational Research Society,2001,52(6):615-622.

[2]MICHALOPOULOS P G,STEPHANOPOULOS G.Optimal control of oversaturated intersection:theoretical and practical considerations[J].Traffic Engineering & Control,1978,19(5):216-221.

[3]CANG T H,LIN J T.Optimal signal timing for an oversaturated intersection[J].Transportation Research Part B:Methodological,2000,34(6):471-491.

[4]CHANG T H,SUN G Y.Modeling and optimization of an oversaturated signalized network[J].Transportation Research Part B:Methodological,2004,38(8):687-707.

[5]LIU H,BSLKE K N,LIN W H.A reverse causal-effect modeling approach for signal control of an oversaturated intersection[J].Transportation Research Part C：Emerging Technologies,2008,16(6):742-754.

[6]楊錦冬,楊東援.城市信號控制交叉口信號周期時長優化模型[J].同濟大學學報(自然科學版),2001,29(7):789-794. YANG Jindong,YANG Dongyuan.Optimized signal time model in signaled intersection[J].Journal of Tongji University(Natural Science)，2001,29(7)：789-794.

[7]曹成濤,徐建閩.單交叉口交通多目標控制方法[J].計算機工程與應用,2010,46(16):20-22. CAO Chengtao，XU Jianmin.Multi object traffic signal control method for single intersection[J].Computer Engineering and Applications,2010,46 (16): 20-22.

[8]祁宏生,王殿海,陳松.基于綜合飽和度的單點信號控制方法[J].哈爾濱工業大學學報,2012,44(2):134-137. QI Hongsheng,WANG Dianhai,CHEN Song.Isolated intersection control based on integrated saturation degree[J].Journal of Harbin Institute of Technology,2012,44 (2): 134-137.

[9]DION F,RAKHA H,KANG Y S.Comparison of delay estimates at under-saturated and over-saturated pre-timed signalized intersections[J].Transportation Research Part B:Methodological,2004,38(2):99-122.

[10]DAGANZO C F.The cell transmission model：A dynamic representation of highway traffic consistent with the hydrodynamic theory[J].Transportation Research Part B：Methodological，1994，28(4)：269-287.

[11]DAGANZO C F.The cell-transmission model：part Ⅱ: network traffic[J].Transportation Research Part B：Methodological，1995，29(2)：79-93.

[12]黃瑋,沈峰,楊曉光.基于細胞傳輸模型的交通流仿真特征及適用性研究[J].交通信息與安全,2008,26(1):19-23. HUANG Wei,SHEN Feng,YANG Xiaoguang.Research on characteristic and applicability of traffic flow simulation based on CTM[J].Journal of Transport Information and Safety,2008,26(1):19-23.

[13]高云峰,韓皓,胡華.信號控制交叉口交通行為的簡單二維元胞傳輸模型[J].系統工程理論與實踐,2015(1):150-159. GAO Yunfeng,HAN Hao,HU Hua.A simple two-dimensional cell transmission model: A dynamic representation of traffic at multiphase signals[J].Systems Engineering-Theory & Practice,2015(1):150-159.

[14]楊東霞,巨永鋒.基于CTM的交通信號多目標優化方法[J].交通運輸工程學報,2011,11 (3):105-111. YANG Dongxia,JU Yongfeng.Multi-objective optimization method of traffic signal based on CTM[J].Journal of Traffic and Transportation Engineering,2011,11(3):105-111.

[15]HONG K L,CHOW A H F.Control strategies for oversaturated traffic[J].Journal of Transportation Engineering,2004,130(4):466-478.

[16]劉金明.基于多目標規劃的城市道路交叉口信號配時研究[D].北京:北京交通大學,2011. LIU Jinming.On signal timing of urban road intersections based on multi-objective programming[D].Beijing：Beijing Jiaotong University,2011.

[17]首艷芳,徐建閩.信號交叉口多目標動態決策模型及其優化方法[J].公路交通科技,2012,29(11):92-97. SHOU Yanfang,XU Jianmin.Multi-objective dynamic decision-making model of signalized intersection and its optimization method[J].Journal of Highway and Transportation Research and Development,2012,29 (11): 92-97.

[18]PHAN V C,ALAM F,POTGIETER J,et al.Integrated fuzzy signal and ramp-metering at a diamond interchange[J].Journal of Advanced Transportation,2013,47(4):413-434.

[19]陳智,劉小明,劉文婷,等.過飽和交叉口交通信號模糊關聯控制方法[J].信息與控制,2014,43(3):374-380. CHEN Zhi,LIU Xiaoming,LIU Wenting，et al.Interconnected control of traffic signals at oversaturated intersections using fuzzy control method[J].Information and Control,2014,43 (3): 374-380.

[20]李瑞敏,陸化普.基于遺傳算法的交通信號控制多目標優化[J].長安大學學報(自然科學版),2009,29(3):85-88. LI Ruimin,LU Huapu.Traffic signal control multi-object optimization based on genetic algorithm[J].Journal of Chang′an University Natural (Science Edition),2009,29 (3): 85-88.

OversaturatedIntersectionControlMethodBasedonCellTransmissionModel

YANGJie，WANGJidong

(SchoolofTransportationandLogistics,SouthwestJiaotongUniversity,Chengdu610031,China)

In order to overcome the practical limitation of the intersection signal control optimization method, the two-dimensional cell transmission model is used to establish the cell transmission model of the signal intersection. The function of intersection saturation degree is used as weight of capacity, the traffic states of all the entrances are taken into consideration in all the intersections, and the penalty function of the oversaturated entrance is introduced and the oversaturated entrance is optimized with priority. Genetic algorithm is used to calculate the dynamic optimization of the intersection signal control. The experiments show that the established model applies to the signal control optimization of both the saturated and unsaturated intersections can effectively reduce the saturation degree of the oversaturated entrance and the whole intersection, and is helpful to improve the through efficiency of the saturated intersection.

signal control optimization; cell transmission model; saturation; capacity; genetic algorithm

U491.51

：A

：1672-0032(2017)03-0030-08

(責任編輯：楊秀紅)

2017-02-20

陽杰(1992—)，男，四川達州人，碩士研究生，主要研究方向為城市交通規劃，E-mail:515896294@qq.com.

10.3969/j.issn.1672-0032.2017.03.005