基于gOMP算法的循環碼譯碼研究
姜恩華
(淮北師范大學 物理與電子信息學院, 安徽淮北 235000)
基于gOMP算法的循環碼譯碼研究
姜恩華
(淮北師范大學 物理與電子信息學院, 安徽淮北 235000)
在壓縮感知理論中,廣義正交匹配追蹤(gOMP)算法常用于解決l0范數的最小化問題.借助無噪聲干擾的壓縮感知觀測模型,提出了循環碼差錯圖案E重構的壓縮感知模型,以校驗矩陣H作為測量矩陣,伴隨式S作為測量信號,采用gOMP算法重構了差錯圖案E,其與收碼R進行模2加運算,求得發碼C的估值.進一步提出了校驗矩陣H作為測量矩陣的構成形式及其2個定理.詳細論述了gOMP算法重構差錯圖案E的計算過程.以(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼為例,分析了gOMP算法對循環碼的糾錯能力;以(7,1)循環碼為例,分析了gOMP算法中原子選取個數s與糾錯位數的關系.通過誤碼率和碼字C重構的成功率,比較分析了gOMP算法和最大似然譯碼算法的譯碼效果.仿真實驗表明,采用壓縮感知理論和廣義正交匹配追蹤gOMP算法實現循環碼譯碼是可行和有效的.
廣義正交匹配追蹤gOMP算法;循環碼;校驗矩陣H;伴隨式S;差錯圖案E
在壓縮感知理論中,廣義正交匹配追蹤(gOMP)算法屬于貪婪算法[1-2],用于解決l0范數的最小化問題.在信道編碼中,循環碼是線性分組碼的一個子類,屬于多項式編碼,主要用于數據存儲和傳輸等通信領域[3].
本文借助無噪聲條件下的壓縮感知理論[4-5],采用校驗矩陣H作為測量矩陣,伴隨式S作為測量信號y,建立了循環碼差錯圖案E重構的壓縮感知模型.通過gOMP算法,正確重構了差錯圖案E,然后對差錯圖案E與收碼R進行模2加運算,計算碼字C的估值.
通過gOMP算法,對(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼進行仿真實驗,通過誤碼率和碼字C估值的成功率,分析gOMP算法的譯碼效果.實驗結果表明,采用gOMP算法能夠實現對(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼的譯碼.
1 差錯圖案E的壓縮感知模型
壓縮感知觀測模型分為無噪聲干擾和有噪聲干擾 2種[4-5].本文借助無噪聲干擾的壓縮感知模型實現差錯圖案E的重構,假設x是稀疏信號,A為測量矩陣,y為測量信號,則y可以表示為[4-5]:
y=A·x,
(1)假設已知測量矩陣A和測量信號y,如式(2)所示[4-5]通過求解‖x‖0范數的最小值求得稀疏信號x.
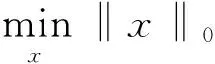
(2)
式(2)為無噪聲干擾的壓縮感知模型,可以通過貪婪算法求解‖x‖0的最小值,例如廣義正交匹配追蹤gOMP算法[1-2].
1.1 差錯圖案E
差錯圖案E等于發碼C減去收碼R,在二元域內,差錯圖案E等于發碼C與收碼R的模2加之和[3]:
E=C⊕R,
(3)
在隨機差錯條件下,通常將差錯圖案E看作一維稀疏信號,由于發碼C與校驗矩陣H正交,其內積為0,式(3)右乘以校驗矩陣H的轉置矩陣HT,由于收碼R和HT的內積定義為伴隨式S,所以伴隨式S與差錯圖案E的關系為[3]
ST=H·ET.
(4)由于式(4)為欠定方程,若每次譯碼都求解式(4),運算量大.在最大似然譯碼算法中,通過查找標準陣列譯碼表得到伴隨式S與差錯圖案E的對應關系.
1.2 求解差錯圖案E的線性規劃模型
根據最佳概率譯碼的準則,選取概率最大的差錯圖案E作為其估值,通過BSC二進制對稱信道可以驗證,重量最輕的差錯圖案E出現的概率最大[3],所以選取重量最輕的差錯圖案E作為其估值,將式(4)作為求解差錯圖案E的約束方程,將求解重量最輕的差錯圖案E作為目標函數,得到求解差錯圖案E的線性規劃模型[6-7]:
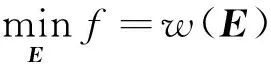
(5)
1.3 重構差錯圖案E的壓縮感知模型
在二元域內,差錯圖案E的元素為0或1,差錯圖案E的重量最輕等效為差錯圖案E的l0范數‖E‖0最小,式(5)的目標函數可以用求解‖E‖0范數最小值代替:
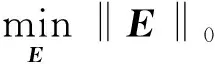
(6)
比較式(6)與式(2)發現,若將差錯圖案E作為一維稀疏信號,伴隨式S作為測量信號,校驗矩陣H作為測量矩陣,可將式(6)定義為重構差錯圖案E的壓縮感知模型.
與文獻[8-10]提供的方法相比,采用壓縮感知理論和gOMP算法重構差錯圖案E不需要查找標準陣列譯碼表,運算量小,計算過程簡單.
2 測量矩陣
若把校驗矩陣H作為測量矩陣,伴隨式S作為測量信號,實現差錯圖案E的重構.校驗矩陣H的稀疏度Spark(H)與差錯圖案E的l0范數‖E‖0之間的關系為[11]
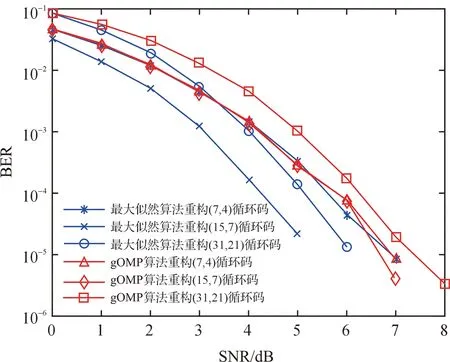
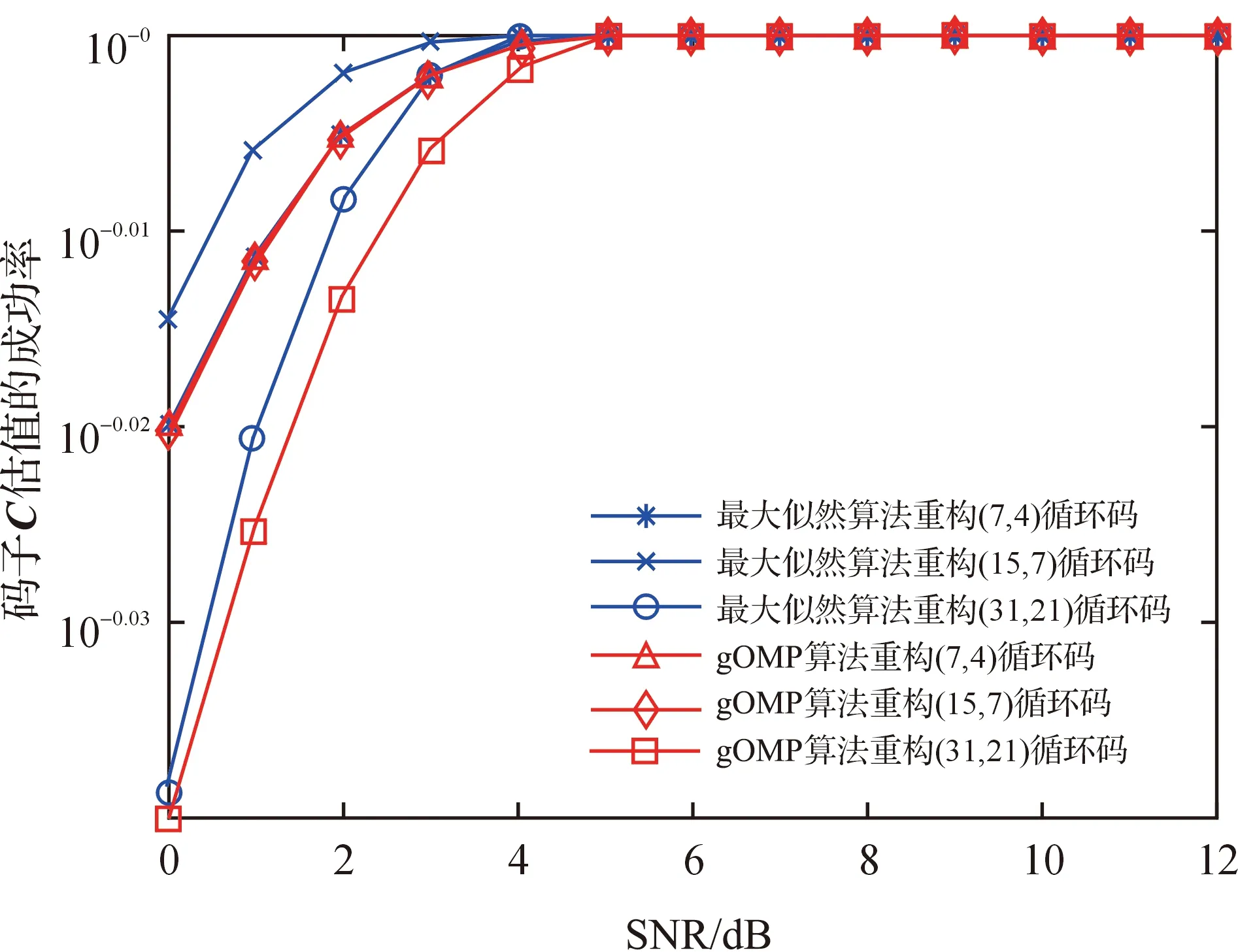
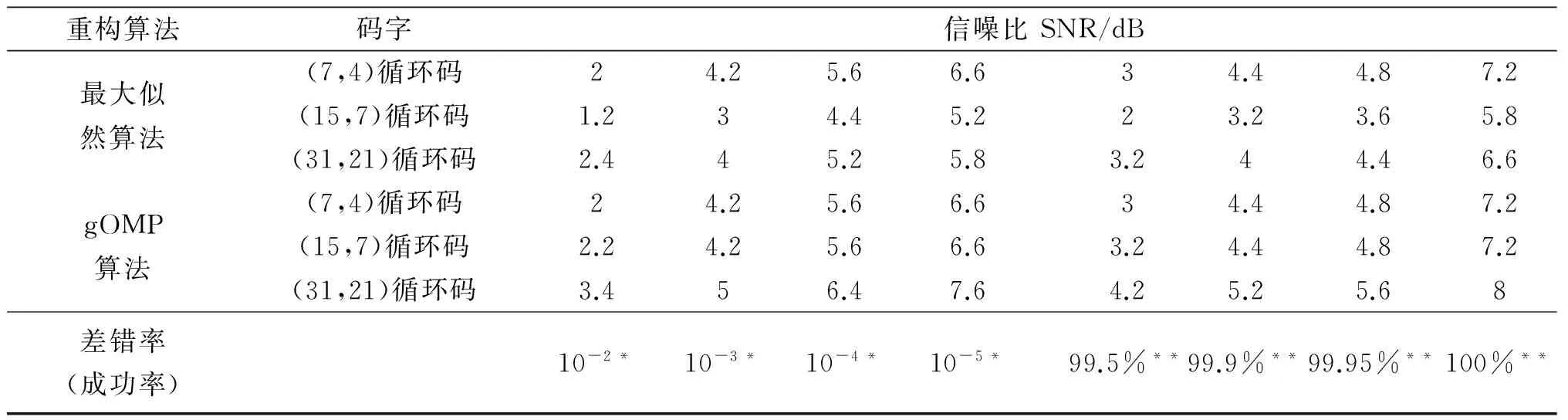
‖E‖0 (7) 校驗矩陣H的構成形式如式(8)所示[12-15]: H=[In-k|P], (8) 其中,子矩陣P的列向量的最小重量為dmin-1,dmin為碼字C的最小距離. 定理1校驗矩陣H的稀疏度Spark為非零碼字的最小重量,即循環碼碼字的最小距離dmin. 證明在循環碼中,校驗矩陣H的稀疏度Spark表示校驗矩陣H中線性相關的最小列數,碼字C與校驗矩陣H正交,所以碼字C與校驗矩陣H的乘積為0,即[15] C·HT=[cn-1,…,c1,c0][hn-1,…,h1,h0]T= (9) 線性分組碼非零碼字的最小重量為碼字的最小距離dmin,碼字C的碼元cn-1,…,c1,c0至少有dmin個非零元素,式(9)至少有dmin個非零項,所以校驗矩陣H至少有dmin個列線性相關,dmin為校驗矩陣H的稀疏度Spark. 定理2差錯圖案E重構的必要條件是差錯圖案E的l0范數小于或等于糾錯能力t. 證明線性分組碼的糾錯能力t為 (10) 由于校驗矩陣H的稀疏度Spark(H)與循環碼碼字的最小距離dmin相等,差錯圖案E的l0范數與校驗矩陣H的稀疏度Spark(H)的關系如式(7)所示,所以有 ‖E‖0≤t. (11) 能使式(11)成立的差錯圖案E就是式(6)最稀疏的解. (12) 當循環碼的校驗矩陣H作為測量矩陣時,可以求出(7,1)循環碼的校驗矩陣H的稀疏度Spark為7,由式(7),計算其差錯圖案E的l0范數最大值為3,根據定理1,其碼字的最小距離dmin=7,根據式(10),(7,1)循環碼的糾錯能力t為3,所以式(11)成立.同理可求得:(7,3)循環碼的校驗矩陣H的稀疏度Spark為4,其差錯圖案E的l0范數最大值為1,(7,3)循環碼的糾錯能力t為1,所以式(11)成立;(7,4)循環碼的校驗矩陣H的稀疏度Spark為3,其差錯圖案E的l0范數最大值為1,(7,4)循環碼的糾錯能力t為1,所以式(11)成立. 將廣義正交匹配追蹤(gOMP)算法[1-2]應用于差錯圖案E的重構,根據差錯圖案E的壓縮感知模型,分析gOMP算法在重構差錯圖案E時的計算過程和譯碼效率. 3.1.1 輸入數據 校驗矩陣H作為測量矩陣,伴隨式S作為測量信號y,差錯圖案E的稀疏度為K,最大原子選擇個數為s. 3.1.2 計算過程 1)參數初始化:求測量矩陣的行數和列數,測量信號y作為初始化殘差r0,索引集合Λ0為空集,按照索引集合Λ0選出的矩陣A0為空集,迭代次數l=1. 2)計算殘差rl=〈rl-1,aj〉,1≤j≤N,并按降序排列,按從大到小的順序選取s個殘差,記錄s個殘差對應的矩陣A的列數j組成列序號集合J0. 3)更新索引集合Λl=Λl-1∪J0和索引集合Λl選出的矩陣Al=Al-1∪aj(j∈J0) . 4)計算y=Al·θl的最小二乘解,計算稀疏信號的估值: 6)判斷殘差rl的值是否小于預設的條件,若小于則跳出循環,或判斷迭代次數l+1后是否大于稀疏度K,若大于則結束循環. gOMP算法通過增加原子選擇的個數s,提高對稀疏信號的重構效率,在文獻[1-2]中,對gOMP、OMP、ROMP、CoSaMP、StOMP算法的重構效率進行了比較,顯示gOMP算法對稀疏信號重構具有優越性. 以(15,7)循環碼為例,采用gOMP算法重構差錯圖案E.(15,7)循環碼的校驗矩陣H如式(13)所示.根據收碼R和校驗矩陣H,計算伴隨式S=R·HT,把伴隨式S作為測量信號,校驗矩陣H作為測量矩陣,通過gOMP算法,重構(15,7)循環碼的差錯圖案E,如表1所示.差錯圖案E也可以通過求解欠定線性方程組S=E·HT得到,求解(15,7)循環碼的差錯圖案E的線性方程組如式(13)所示,若(15,7)循環碼的糾錯位數取1,將重量為0或1的差錯圖案E代入線性方程組式(13),求出伴隨式S,列出標準陣列譯碼表,與表1比較,可以驗證gOMP算法重構的差錯圖案E是正確的.同理,也可以采用gOMP算法正確重構(7,1)、(7,3)、(7,4)和(31,21)循環碼的差錯圖案E. (13) 表1 gOMP算法重構(15,7)循環碼的差錯圖案E的結果 采用gOMP算法,實現(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼的糾錯,分別采用各自的校驗矩陣H作為測量矩陣,分析gOMP算法對循環碼的糾錯能力以及gOMP算法中原子選擇的個數s對循環碼糾錯位數的影響. 以(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼為例,測試gOMP算法對循環碼的糾錯能力,把差錯位數從0逐漸增加,能被100%重構的收碼的最大差錯位數為其糾錯能力t,因為測量信號長度M=n-k是伴隨式S的長度,采用校驗矩陣H作為測量矩陣,伴隨式S作為測量信號,差錯位數為差錯圖案E中1的個數.實驗結果如圖1所示,可以看出goMP算法對差錯位數為3的(7,1)循環碼的糾錯能力為100%,對差錯位數為1的(7,3)、(7,4)、(15,7)和(31,21)循環碼的糾錯能力為100%.同時可看出gOMP 算法對(7,3)、(15,7)和(31,21)循環碼中差錯位數為2和3的收碼也有一定的糾錯能力.對差錯位數為2的(15,7)循環碼的糾錯能力為60%.(7,3)和(31,21)循環碼的糾錯能力近似相同. 在每次迭代時,gOMP算法計算傳感矩陣A各列與殘差的內積,并按照降序排列,依次選擇s個最大的殘差來更新索引集合,提高了gOMP算法的重構效率.以(7,1)循環碼為例,選擇s=2,3,4,測試gOMP算法對(7,1)循環碼的糾錯能力,如圖2所示,可以看出s=2時,能糾正3位錯誤,s=3時,能糾正2位錯誤,s=4時,能糾正1位錯誤,所以原子個數s=2為最佳選擇,能夠實現(7,1)循環碼的糾錯能力為3.同理,可以驗證:(7,4)循環碼在s=3時,對差錯位數為1的收碼重構的成功率為100%.(7,3)循環碼在s=1,2,3,4時,對差錯位數為1的收碼重構的成功率為100%,當s=4時,對差錯位數為2的收碼的糾錯能力為30%.(15,7)循環碼在s=1,2,3,4時,對差錯位數為1的收碼重構的成功率為100%,當s=3時,對差錯位數為2的收碼的糾錯能力為80%.(31,21)循環碼在s=1,2,3,4時,對差錯位數為1的收碼重構的成功率為100%,當s=1時,對差錯位數為2的收碼的糾錯能力為35%. 圖1 測量信號長度M對循環碼糾錯能力的影響 圖2 原子選擇個數s對(7,1)循環碼糾錯能力的影響(M=6,N=7) 按照如圖3所示的線性分組碼的譯碼步驟設計仿真實驗[3],首先產生N個信息元組m,信息元組m與生成矩陣G相乘生成碼字C,對碼字C進行2PSK調制,已調信號通過高斯白噪聲信道AWGN,信噪比SNR取值范圍為0~12 dB,在每個信噪比SNR點,選取N=50 000個m信息分組.在接收端,對接收信號進行2PSK解調,得到收碼R,借助校驗矩陣H計算伴隨式S.將伴隨式S作為測量信號,校驗矩陣H作為測量矩陣,通過廣義正交匹配追蹤gOMP算法,重構差錯圖案E,重構的差錯圖案E與收碼R進行模2加運算,計算碼字C的估值. 圖3 線性分組碼的編譯碼過程 借助Matlab軟件編寫程序,實現 gOMP算法和最大似然譯碼算法對循環碼譯碼的仿真實驗,本文以(7,4)、(15,7)和(31,21)循環碼為例,從譯碼的誤碼率和碼字C重構的成功率兩方面比較gOMP算法和最大似然譯碼算法的譯碼效果[16],譯碼的誤碼率如圖4所示,碼字C重構的成功率如圖5所示. 圖4 循環碼譯碼的誤碼率比較 圖5 循環碼譯碼的碼字C估值成功率比較 從圖4中可以看出,在同一個譯碼算法中,(15,7)循環碼譯碼的誤碼率最低.當信噪比SNR相同時,最大似然算法譯(15,7)循環碼的誤碼率最低,當信噪比SNR為5.2 dB時,其誤碼率低于10-5.gOMP算法譯(31,21)循環碼的誤碼率最高,當信噪比SNR為7.6 dB時,其誤碼率低于10-5.采用最大似然算法和gOMP算法譯(7,4)循環碼的誤碼率近似相同,當信噪比SNR為6.6 dB時,其誤碼率低于10-5.gOMP算法譯(15,7)與(7,4)循環碼的誤碼率近似,當信噪比SNR為6.6 dB時,其誤碼率低于10-5.從圖5中可以看出,最大似然算法譯(15,7)循環碼的碼字C重構的成功率最高,在信噪比SNR為5.8 dB時,碼字C重構的成功率趨于100%.采用最大似然算法和gOMP算法譯(7,4)循環碼的碼字C重構成功率近似,當信噪比SNR為7.2 dB時,碼字C重構的成功率趨于100%.gOMP算法譯(15,7)與(7,4)循環碼碼字C重構成功率近似,當信噪比SNR為7.2 dB時,碼字C重構的成功率趨于100%.當信噪比相同時,gOMP算法譯(31,21)循環碼的碼字C重構成功率低于最大似然算法;當信噪比SNR為6.6 dB時,最大似然算法重構(31,21)循環碼的成功率趨于100%;當信噪比SNR為8 dB時,gOMP算法重構(31,21)循環碼的成功率趨于100%.gOMP算法和最大似然算法重構(7,4)、(15,7)和(31,21)循環碼的差錯率和成功率如表2所示. 表2 循環碼重構的差錯率和成功率 *為差錯率,**為成功率. 通過分析仿真實驗結果得到:采用gOMP算法能夠實現(7,4)、(15,7)和(31,21)循環碼的譯碼.與最大似然譯碼算法相比,在循環碼譯碼的成功率趨于100%的條件下,gOMP算法譯碼時的信噪比SNR比最大似然算法大1.4 dB.但gOMP算法是根據伴隨式S和校驗矩陣H重構差錯圖案E的,從而計算出碼字C的估值,不需要查找標準陣列譯碼表,即可實現對(7,4)、(15,7)和(31,21)循環碼的譯碼. 借助無噪聲干擾壓縮感知的觀測模型,提出了求解差錯圖案E的線性規劃模型和壓縮感知模型.采用gOMP算法實現(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼的譯碼,提出了校驗矩陣H作為測量矩陣的構成形式和2個定理.采用伴隨式S作為測量信號,通過gOMP算法重構差錯圖案E,對E與收碼R進行模2加運算,計算發碼C的估值.借助(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼,分析了gOMP算法對循環碼的糾錯能力及gOMP算法中原子選取個數s與糾錯位數的關系.通過譯碼的誤碼率和碼字C重構的成功率,比較分析了gOMP算法和最大似然譯碼算法對(7,4)、(15,7)和(31,21)循環碼的譯碼效果.實驗結果表明:采用gOMP算法能夠實現對(7,1)、(7,3)、(7,4)、(15,7)和(31,21)循環碼的譯碼. [1]JIANW,SEOKBEOPK,BYONGHYOS.Generalizedorthogonalmatchingpursuit[J].IEEETransactionsonSignalProcessing,2012,60(12):6202-6216. [2] WANG J, KWON S, LI P, et al. Recovery of sparse signals via generalized orthogonal matching pursuit: A new analysis[J].IEEETransactionsonSignalProcessing,2016,64(4):1076-1089. [3] 曹雪虹,張宗橙.信息論與編碼[M].第2版,北京:清華大學出版社,2009. CAO X H, ZHANG Z C.InformationTheoryandCoding[M]. 2nd ed. Beijing: Tsinghua University Press,2009. [4] CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J].IEEETransactionsonInformationTheory,2006,52(2):489-509. [5] DONOHO D L. Compressed sensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306. [6] DASKALAKIS C, DIMAKIS A G, KARP R M, et al. Probabilistic analysis of linear programming decoding[J].IEEETransactionsonInformationTheory,2008,54(8):3565-3578. [7] DIMAKIS A G, VONTOBEL P O. LP decoding meets LP decoding: A connection between channel coding and compressed sensing[C]//Forty-SeventhAnnualAllertonConference. Illinois:IEEI,2009:8-15. [8] 李耀輝,趙海豹,馬春芽.循環碼譯碼的Dixon結式 方法[J].應用數學學報,2011,34(4):602-617. LI Y H, ZHAO H B, MA C Y. Decoding cyclic codes by using Dixon resultant method[J].ActaMathematicaeApplicataeSinica,2011,34(4):602-617. [9] AUGOT D, BARDET M, FAUGRE J C. On the decoding of binary cyclic codes with the Newton identities[J].JournalofSymbolicComputation,2009,44(12):1608-1625. [10] LOUSTAUNAU P, YORK E V. On the decoding of cyclic codes using Gr?bner bases[J].ApplicableAlgebrainEngineeringCommunication&Computing,1997,8(6):469-483. [11] ELAD M.SparseandRedundantRepresentations:FromTheorytoApplicationsinSignalandImageProcessing[M]. New York:Springer Publishing Company,2010:26-30. [12] LIN L, LIU F, JIAO L. Compressed sensing by collaborative reconstruction on over complete dictionary [J].SignalProcessing,2014,103:92-102. [13] 董小亮,楊良龍,趙生妹,等.用信道編碼構造壓縮感知測量矩陣[J].信號處理,2013,29(7):809-815. DONG X L, YANG L L, ZHAO S M, et al. Channel coding for compressed sensing measurement matrix[J].JournalofSignalProcessing,2013,29(7):809-815. [14] 蘆存博,肖嵩,權磊.基于二進制序列族的壓縮感知測量矩陣構造[J].電子與信息學報,2016,38(7): 1682-1688. LU C B, XIAO S, QUAN L. Construction of compressed sensing measurement matrix based on binary sequence family[J].IntroductionofJournalofElectronics&InformationTechnology,2016,38(7): 1682-1688. [15] 張景雄,陽柯,郭建中.壓縮感知的信息論解譯[J].武漢大學學報:信息科學版,2014,39(11):1261-1268. ZHANG J X, YANG K, GUO J Z. Information-theoretic interpretations of compressive sampling[J].GeomaticsandInformationScienceofWuhanUniversity,2014,39(11):1261-1268. [16] 張軼,達新宇,褚振勇.低密度奇偶校驗碼的壓縮感知重構[J].吉林大學學報:工學版,2015,45(3): 985-990. ZHANG Y, DA X Y, CHU Z Y. Compressed sensing reconstruction of LDPC code[J].JournalofJilinUniversity:EngineeringandTechnologyEdition,2015,45(3): 985-990. JIANG Enhua (School of Physics and Electronic Information, Huaibei Normal University,Huaibei 235000,Anhui Province,China) The generalized orthogonal matching pursuit gOMP algorithm has been used in the compressed sensing theory to solve the minimizing problem of thel0norm. According to the compressed sensing model under the no noise condition, the compressed sensing model of the reconstructing error patternEof the cyclic code is built in this paper. With the check matrixHas the measurement matrix, the syndromeSas the measurement signal, the error patternEis reconstructed using the gOMP algorithm, while the value of the code wordCis calculated by the receiving codeRadding the error patternEon modulo 2. Furthermore, we provide the form of the check matrixH, and propose two relevant theorems. The error correction ability of the gOMP algorithm is analyzed through some cyclic code examples, and the relationship between the selecting atom numbersof the gOMP algorithm and the error correction bits is investigated. Finally, based on the bit error rate and the code wordCreconstructing success rate, the decoding effects of the gOMP algorithm and the maximum likelihood algorithm are analyzed and compared. The simulation experiment results prove that the compressed sensing theory and gOMP algorithm are feasible and effective in decoding the cyclic code. generalized orthogonal matching pursuit(gOMP)algorithm; cyclic code; check matrixH; syndromeS; error patternE TN 911.7 :A :1008-9497(2017)05-555-06 2016-06-30. 國家自然科學基金資助項目(41475017, 11504121);安徽省高校自然科學研究重點項目(KJ2016A628,KJ2016A650). 姜恩華(1974-),ORCID: http:// orcid.org/0000-0002-5944-4541,男,碩士,副教授,主要從事數字通信技術與信息處理研究,E-mail:jianghnhb@126.com. 10.3785/j.issn.1008-9497.2017.05.010 ResearchonthecycliccodesdecodingbasedonthegeneralizedorthogonalmatchingpursuitgOMPalgorithm.Journal of Zhejiang University (Science Edition),2017,44(5):555-560,575
cn-1·hn-1+…+c1·h1+c0·h0=0.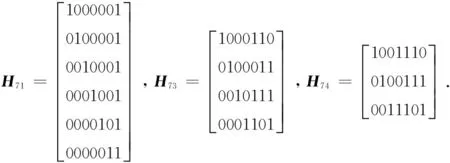
3 廣義正交匹配追蹤(gOMP)算法
3.1 gOMP算法重構差錯圖案E的計算過程
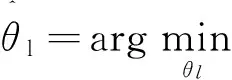
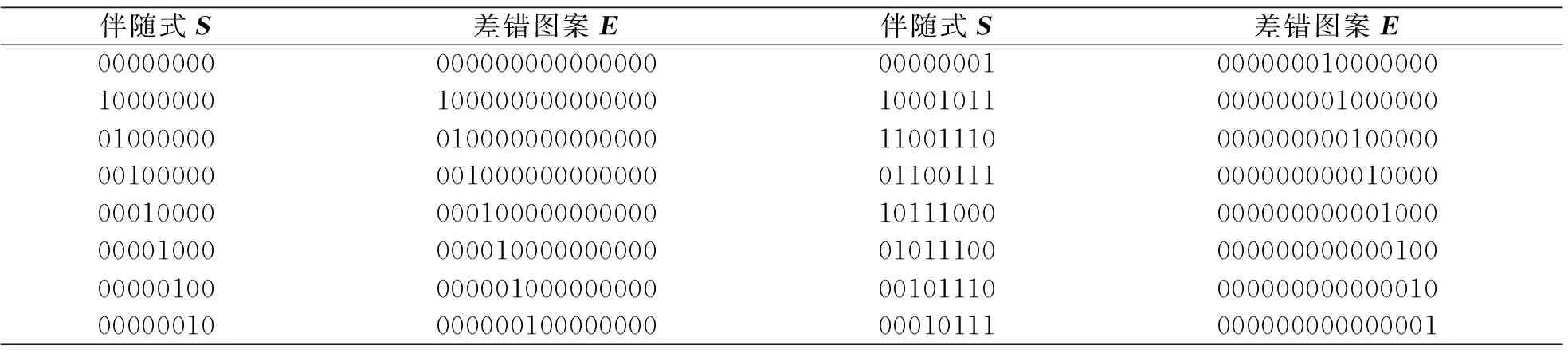
3.2 差錯圖案E重構
4 gOMP算法的循環碼譯碼效果分析
4.1 gOMP算法的循環碼糾錯能力
4.2 原子選擇個數s對循環碼糾錯的影響
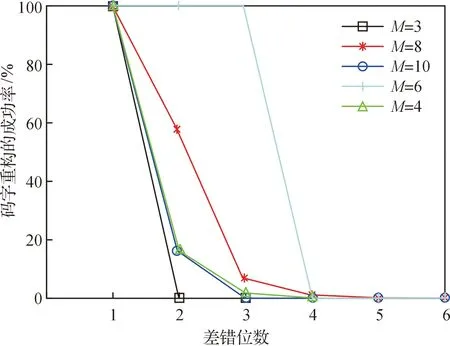
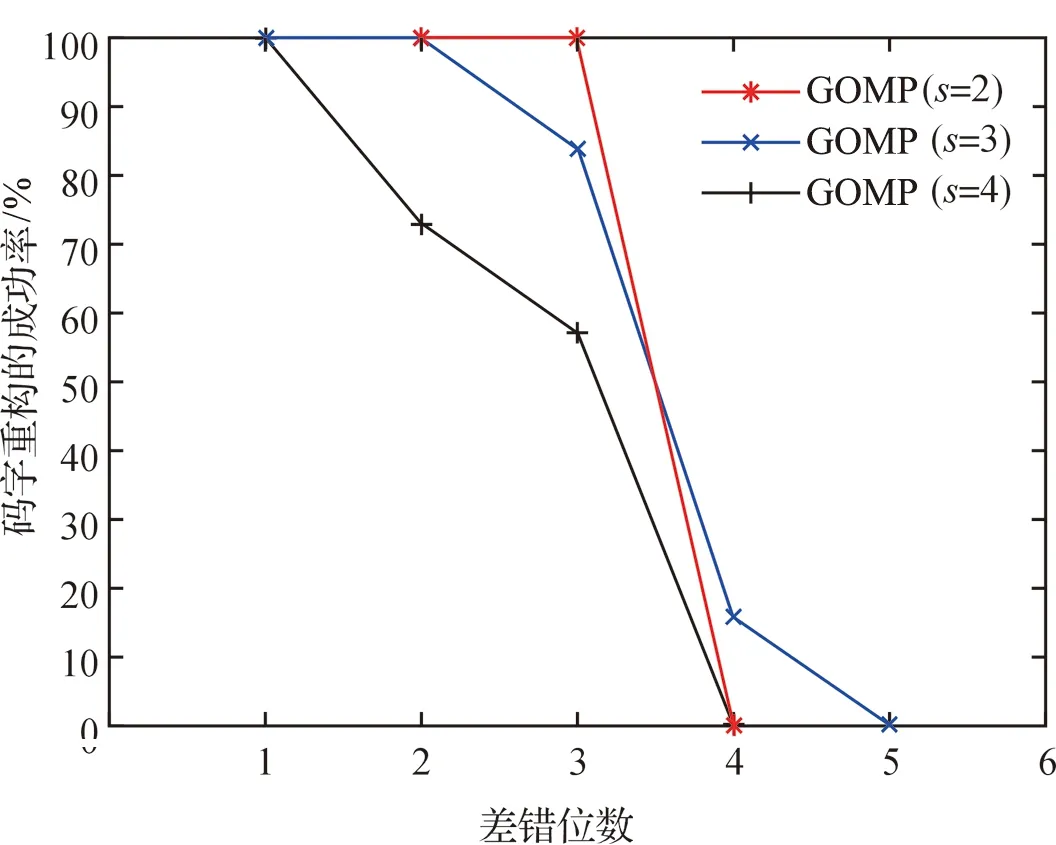
5 循環碼譯碼的仿真實驗設計
5.1 仿真實驗設計

5.2 gOMP算法實現循環碼譯碼
6 結 語


