投資活動中風險偏好的度量與研究

楊雁雁

（武夷學院 數學與計算機學院，福建 武夷山 354300）

投資活動中風險偏好的度量與研究

楊雁雁

（武夷學院 數學與計算機學院，福建 武夷山 354300）

投資者的活動離不開人的主觀感受與對風險的偏好，本文首先從馮諾依曼的可測效用公理出發，引用期望效應函數來描述有風險偏好的投資人的投資效用，并從定常風險和非定常風險偏好的角度給出期望效用函數計算方法與風險偏好的度量.其次從風險價值度角度，利用不同風險偏好者對風險與收益關注度的不同，給出了VAR(CVAR)模型下的風險偏好度量.最后由投資心理和偏好心理的復雜性，通過預設風險偏好性質來度量風險偏好，以增加靈活性與實用性.

期望效用；風險偏好；VAR理論；預設風險偏好性質

1 引言

隨著中國金融業的發展，投資人在追求利潤最大化的同時，不可避免要考慮風險因素.對相同的經濟結果，投資者看重的是相對結果而不是絕對結果[1].在做決策時，必然在考慮收益的同時也要考慮風險損失，即收益與損失的聯合效用.風險偏好者實施冒險的經濟行為，風險規避者施行保守的經濟決策.如何衡量這種風險偏好，使投資者在一定風險偏好下做出最理性決策是研究者需要研究的.

風險偏好的度量很重要，只有充分度量投資者的風險偏好，金融機構才能根據投資者的風險偏好設計相應的理財產品，增加理財產品的銷量；實業公司才可以根據自己的風險偏好確定與其相一致的經營策略，實現經濟運營效用最大化；投資者才可以根據自己的風險偏好，通過效用函數的構建，對自己的經濟行為及時預警，防止不利經濟決策的出現.然而現有研究對風險偏好的度量尚無系統化的闡述，即使在涉及投資問題時提及風險偏好，也僅作為條件判斷的切入點，缺乏模型化的描述.本文從主流的研究投資活動的理論出發，對風險偏好進行度量和研究.研究投資活動的主流方法有馬克維茨的均值方差理論，馮諾依曼的期望效用函數理論和風險價值度理論.馬克維茨的均值方差理論要求一定收益下風險最小，并不能有效衡量投資者風險偏好的差異性，它實際上是附加了條件的期望效用函數最大化問題.

風險偏好作為一種偏好，是投資者對投資結果中收益和風險聯合效用主觀滿意度的選擇.本文從馮諾依曼的涉及偏好的四條公理出發，引入風險偏好的概念，再根據可測效用公理引出的期望效用函數，來描述風險中性者、風險厭惡者、風險愛好者的度量問題.然而可測效用公理只給出抽象的期望效用函數概念，并沒有給出具體的區分不同風險偏好的效用函數.本文從風險偏好隨財富水平不變和變化兩個角度來求解度量風險偏好的期望效用函數，并發現在具體的求解過程中，賭博當量的確定非常重要，本文通過一個例子來說明具體的期望效用函數的求解方法.考慮到人對當前的感受要強于對未來的感受,投資者把高于一定數值的收益不看成風險，而把低于一定數值的收益看成風險，本文從VAR(CVAR)理論出發來描述風險,通過不同風險偏好者對收益和風險的關注程度的不同，來構建相應的度量風險偏好的效用函數.最后由于投資心理和偏好心理的復雜性，通過預設偏好性質來度量風險偏好，以增加靈活性與實用性.

對于風險偏好的度量，前人已做了相應的工作.馮諾依曼-摩根斯特恩在投資活動和經濟行為中給出了涉及偏好的可測效用公理[2].劉宗謙[3]等給出了期望效用存在性的證明.姜青舫[4]對定常風險效用函數的導出給出了證明.徐緒松[5]從期望效用最大化的角度研究了損失規避下的投資組合問題.許民利[6]等通過條件價值建立相應的偏好決策模型.

2 期望效用函數下的風險偏好度量

理性投資者追求的是收益最大化，然投資活動的收益伴隨著風險，投資者對風險的厭惡程度直接影響其經濟決策，如何衡量這種風險偏好，從而在一定風險偏好程度下作出最理性的決策，即一定風險偏好下收益最大化，是我們研究的問題.這里有兩點需要明確，一是風險偏好，二是收益最大化.我們把收益與風險的聯合作用對投資者主觀滿意度的影響稱為效用，在不確定條件下我們用期望效用來描述收益與風險的聯合作用.

2.1 風險偏好的定義與期望效用函數的描述

假設把投資的收益看成一種“商品”或“價值”.定義“未定價值空間”?，它是由“確定價值空間”的向量x,y等形成形如L={(x,y,p)|0≤p≤1}的組和更高層次的組?={(L1,L2,p)|0≤p≤1}所形成的集合.其中(x,y,p)表示取x的概率為p，取y的概率為1-p.在?上定義一種偏好關系?，滿足馮諾依曼-摩根斯特恩四條公理，其具體描述如下：

公理 1 (i)x?x；

(ii)如果 x?y，y?z則 x?z；

(iii)x?y和y?x至少有一個成立；

公理 2 (i)x=(x,y,1)；

公理3 對于?x,y,z∈?，{p∈[0,1]|(x,y,p)?z}和p∈[0,1]|z?(x,y,p)}都是閉集.

公理 4 如果 x～y,?p∈[0,1]和 z∈?，(x,zp)～(y,z,p).

其中符號～表示無差異量，從偏好的角度來說，x～y表示價值相等的量，也叫賭博當量.記(x,p,y)～τ，不同風險偏好所取的τ值不同.當E(x,p,y)=τ時，稱該經濟活動者為風險中性者，當E(x,p,y)＜τ時，該經濟活動者為風險追求者；當E(x,p,y)＞τ時，該經濟活動者為風險厭惡者.更一般的我們可以由期望效用函數描述這三種風險偏好，事實上有以下結論：如果(?,?)滿足上述四條公理，則在?上存在惟一的期望效用函數 u，滿足：x?y，且僅當 u(x)≥u(y),u(x,y,p)=pu(x)+(1-p)u(y).

上述結論的證明可以參考文獻[3]，接下來我們通過期望效用函數來具體度量風險偏好.假設x表示發生風險事件的收益，y表示未發生風險事件的收益，p表示發生風險事件的概率，構造L={(x,y,p)|0≤p≤1}.由投資人的風險偏好決定的期望效用函數為u(x)，投資者對(x,y,p)這一風險事件所包含的風險態度可由u(px+(1-p)y)=u(x,y,p)的比較來刻畫，如果有

成立，那么稱該經濟活動者為風險中性者；

如果有

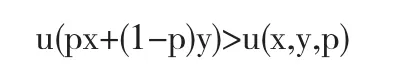
成立，稱該經濟活動者為風險厭惡者；如果有

成立，稱該經濟活動者為風險愛好者.

2.2 風險偏好的期望效用函數度量

當財富水平的變化不改變風險偏好時，即滿足(x,p,y)～τ?(x,p,y)+ω～τ+ω時，我們稱其為定常風險偏好，對上式兩端同時帶入期望效用函數中運算可得

若u(x)在R上不恒為零、嚴格單調且連續可微，則按加法定理可以證明，當投資者為風險中性時，投資者的效用函數為u(x)=bx+d，當投資者為風險偏好或風險厭惡時，其期望效用函數u(x)=(ebcx-1)/c+d.具體的證明可以詳見文獻[4].

對u(x)取二階導數，可得u(x)"=b2cebcx，當c＞0時，此時u(x)"＞0，對應的投資者為風險厭惡者，其風險厭惡程度-bc.當c＜0時，此時u(x)"＞0，對應的投資者為風險偏好者，其風險厭惡程度-bc.

假設x0表示發生風險事件的收益，y0表示未發生損失事件后的收益，發生損失時的概率為1/2，為簡便起見，令u(x0)=0，u(y0)=1.假設投資者的賭博當量(x0,y0,1/2)～τ，令 z(x)=(x-x0)/(y-y0)，且 z(τ0)=1/4，聯立 u(x0)=0，u(y0)=1，(x0,y0,1/2)～τ0可得其期望效用函數為u(x)=1.7841(1-e-0.8221(x-x0)/(y0-x0))，是風險厭惡的情況，其厭惡程度為0.8221/(y0-x0).

當財富水平改變風險偏好時，我們稱其為非定常風險偏好，顯然這在現實中更加普遍.若所取時間段很短，且在這個時間段內沒有發生最嚴重的損失事件，可以假設財富變化對風險偏好的變化的影響不顯著，我們仍然可以采用上述定常風險偏好的結論，其關鍵是對投資者賭博當量的測試，例如在當前財富水平下，賭博當量為(1,0,1/3)～1/2，u(x0)=0，u(y0)=1，所求得的期望效用函數是在當前財富水平下，很小時間段內的期望效用函數,對應的是風險追求的情況，其風險厭惡程度為-1.3863/(y0-x0).

3 VAR(CVAR)模型下的風險偏好度量

考慮到投資者對損失的敏感性，投資者僅把低于一定數值的收益看成風險，我們把收益區間進行分割，分為高盈利部分和低盈利部分，這里的低盈利部分就是投資者認為的風險損失部分，是投資者不希望出現的.高盈利部分是投資者認為的收益部分，是投資者所追求的.高盈利部分發生的概率為β，低盈利部分為1-β.接下來我們從CVAR模型和VAR模型來對不同風險偏好進行度量和研究.

風險規避者不僅關注自身利潤，更關注風險損失情況，用CvaR衡量大于某一損失水平部分的損失期望.在給定的容忍損失水平下，風險規避者要求在這一損失水平下利潤值的期望最大，即損失發生時其利潤部分的期望值最大.給定某一置信水平β，β∈(0,1)，π表示收益情況，

其中Z1-β是概率為1-β時對應的分位數.CvaR為利潤水平低于VaR的利潤期望，則

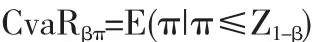
當投資者為風險規避者時，其更關注風險損失部分的收益，目標函數為max{CvaRβπ}.當投資者為風險偏好者時，風險偏好者更關注高盈利部分的收益，即在β置信水平上，風險偏好者要求利潤值不低于Z1-β的收益期望最大.風險偏好投資者的決策模型為：

不同風險偏好者對高收益部分與低收益部分關注程度也不同.為了準確度量風險偏好，假設高收益部分的占比為λ，收益期望記為E1，低收益部分占比為(1-λ)，收益期望記為E2.假設收益的密度函數為f(x)，則

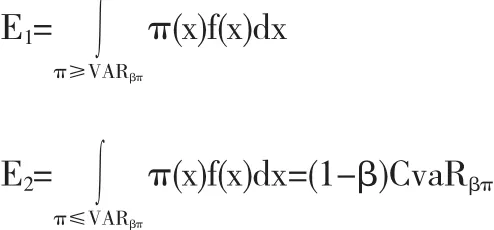
風險偏好可以通過函數λE1(1-λ)E2來度量，當λ=1/2時，表示對風險和收益持相同的關注度，為風險中性.當λ＞1/2時，表示更關注收益部分，為風險追求者，且λ越大其風險厭惡程度越低.當λ＜1/2時，表示更關注風險損失部分，為風險厭惡者，且λ越小其風險厭惡程度越高.

4 設定偏好性質的風險偏好度量

除了從期望效用函數和風險價值度的角度來度量風險偏好，投資者還可以根據實際情況設定風險偏好的性質來度量風險偏好.假設投資者更加關注安全性和期望收益，設As是投資者能容忍的收益底線，從投資者的心理感受出發，用變量的實際值小于As來表示風險，即X≤As，當X＞As時表示資金安全，未來收益不低于As的概率為Ps，用p來衡量對安全性指標的重視程度.則投資者的風險偏好可以由效用函數u(x)=PSpE(x)(1-p)來度量.p值越大表明越重視安全性.

設收益X對應的概率密度函數為f(x)，則有

其中As與p由投資者的偏好性質預先設定.在這種風險偏好度量方法中，投資者根據歷史數據得出收益的分布情況，并求出收益的概率密度函數，As是投資者容忍的收益底線，p值的確定可以由投資者過往的投資決策結合當下的風險偏好情況得出，主觀性強.

類似的，在預設風險偏好性質的度量中，投資者可以根據自己的風險厭惡程度，通過預設δ值調整收益率來度量風險，δ表示對風險重視程度.如果投資者對風險厭惡程度重，則設置δ＜1,反之，對債券的長期價值比較樂觀，為減少對風險的敏感度，則設置δ＜1.通過風險偏好的不同而調整的收益率z可以表示成如下形式:

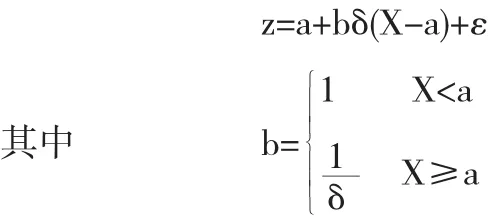
a表示投資者平均收益率，X為實際收益率，ε表示決策者對收益率波動誤差的估計，在實踐中一般假設ε服從正態分布.δ取值大小由投資者的風險偏好程度預先設定，b的設置是為了確保δ的取值關注的是風險造成的損失，而不會同時放大收益，造成誤判.

在設定風險偏好性質的風險偏好度量中，參數的選取完全由投資者的風險厭惡程度決定，且度量風險偏好的效用函數不是唯一的，它由投資者的實際需要和風險偏好的性質共同決定.與期望效用函數和條件在險價值法度量風險偏好的方法相比更加靈活且操作性更強，但由于其主觀性更強且誤差更大，在不需要對風險偏好精確度量的情況下可以作為度量風險偏好的重要補充.

〔1〕賀書婕.風險量化工具的決策價值[J].觀察思考，2016（05）.

〔2〕von Neumann JO Morgenstern.Theory of games and economic behavior[M].Princeton,N J:Princeton University Press,1947.

〔3〕劉宗謙，付衛強，馮素芬.期望效用函數存在定理的另一種證明[J].首都師范大學學報，2008（04）.

〔4〕姜青舫.一種隨機特殊函數方程的解法及定常風險厭惡效用函數的導出[J].貴州科學,1998,16(4):261-265.

〔5〕徐緒松,馬莉莉,陳彥斌.考慮損失規避的期望效用投資組合模型[J].中國管理科學,2007（10）.

〔6〕許民利，聶曉哲，簡惠云.不同風險偏好下雙渠道供應鏈定價決策[J].控制與決策，2016（01）.

〔7〕史樹中.金融經濟學十講[M].上海：上海人民出版社，2011.131-132.

〔8〕Jorion P(菲利普.喬瑞).風險價值 VaR[M].中信出版社，2005.400.

〔9〕李平，黃光東，路陽.基于Copula理論的多心理賬戶組合VaR模型與基金風險管理[J].系統工程理論與實踐，2011（05）.

O29

A

1673-260X（2017）09-0003-03

2017-06-11