基于優化支持向量機-混沌BP神經網絡的基坑變形預測研究

王興科， 王 娟

(陜西鐵路工程職業技術學院， 陜西 渭南 714000)

基于優化支持向量機-混沌BP神經網絡的基坑變形預測研究

王興科， 王 娟

(陜西鐵路工程職業技術學院， 陜西 渭南 714000)

為解決基坑變形預測精度低的問題，采用小波去噪分離基坑變形的趨勢項及誤差項序列，并利用多種優化的支持向量機對趨勢項序列進行預測，采用混沌BP神經網絡對誤差項序列進行預測，將兩者預測結果進行疊加即得到變形預測值，且可根據后期監測數據的更新，實時增加數據信息，達到跟蹤預測的目的。經過3個實例檢驗，得出小波函數的去噪效果相對較優，且預測結果的相對誤差均值均小于2%，驗證了優化支持向量機-混沌BP神經網絡模型的有效性，且該模型具有預測精度高、 適用性強等優點，對掌握基坑變形的發展趨勢及評價基坑的穩定性具有重要意義。

基坑變形預測； 小波去噪； 支持向量機； BP神經網絡； 趨勢項預測； 誤差項預測

Abstract: The accuracy of deformation prediction of foundation pit is low by using traditional methods. As a result, the tendency item and error item sequence of foundation pit deformation are separated by wavelet; the tendency item sequence is predicted by some optimized support vector machines; the error item sequence is predicted by chaotic BP neural network. The deformation prediction results of foundation pit can be obtained by superposition of the two prediction results; and the tracing prediction can be realized by adding later monitoring data uploading. According to case study results, the denoising effect of the wavelet functions are relatively superior and the mean relative error of the prediction results are less than 2%, which verify the validity, prediction accuracy and high adaptability of the optimized support vector machine-chaotic BP neural network model.

Keywords: foundation pit deformation prediction; wavelet denoising; support vector machine; BP neural network; tendency item prediction; error item prediction

0 引言

目前，基坑已成為城市建設中的重要建設項目之一，也是巖土領域的研究熱點。在基坑的穩定性評價中，基坑變形能簡單有效地反映基坑的穩定現狀，并已被廣泛應用到工程實踐中，且通過對監測數據的預測，能更有效地掌握基坑未來的變形趨勢，對優化施工過程具有重要的意義。但在現場監測過程中，常會遇到一些不確定因素，難以獲得基坑變形的準確信息。基坑的原始變形數據含有誤差信息是必然的，而誤差信息會增加原始監測數據的不確定性和隨機性，勢必會影響預測精度。為達到提高預測精度的目的，對原始監測數據進行分離預測，即把原始數據分離為趨勢項和誤差項，使趨勢項具有更好的規律性。在趨勢項與誤差項的分離過程中，楊哲峰等[1]將小波去噪引入到基坑變形數據的去噪過程中，通過小波去噪達到了剔除基坑變形數據誤差信息的目的，因此，也采用小波去噪對基坑的變形數據進行去噪處理，并分離趨勢項與誤差項。同時，支持向量機也是基坑變形預測的常用方法之一，但該方法對使用者的經驗依賴性較大，為提高該方法的適用性和有效性，許多學者對其參數優化進行了研究，如姜彥作等[2]、曹凈等[3]、林楠等[4]采用最小二乘法對支持向量機進行優化，該方法具有泛化能力強、收斂速度快等優點，經過工程實例檢驗，驗證了該優化模型具有較高的預測精度，實用價值較高； 曹凈等[5]、彭磊等[6]則是將粒子群算法引入到支持向量機的優化過程中，該優化算法能很大程度地提高支持向量機的全局優化能力，也具有較好的泛化能力。經實例檢驗，該優化模型也具有較好的預測精度，可行性較強，所以將最小二乘法和粒子群法優化的支持向量機作為基坑趨勢項的預測模型。同時，誤差項序列含有較多的誤差信息，具有顯著的混沌特征，因此利用混沌BP神經網絡對誤差項進行預測，如王江等[7]利用混沌優化算法對BP神經網絡進行優化和改進，克服了BP神經網絡的缺陷，實例檢驗該模型的預測精度較高。綜上所述，將多種預測模型進行合理的結合，構建基坑變形的綜合預測模型，該模型能利用多種模型的優點，綜合性強，可提高基坑變形的預測精度，進而滿足工程實際的需要。

1 基本原理

1.1 論文思路及預測過程

1.1.1 論文思路

論文的基本思路為： 利用3次樣條插值將非等距序列轉變為等距序列，并采用小波去噪對監測數據進行去噪處理，將基坑變形序列劃分為趨勢項和誤差項； 同時，利用多種優化支持向量機模型對基坑變形的趨勢項進行預測，再利用混沌BP神經網絡對誤差項進行預測，進而將兩者的預測結果進行疊加，實現基坑變形的綜合預測。并根據監測過程中的數據更新，實時更新數據，以實現基坑變形的滾動預測。

該預測方法具有如下特點：

1)能實現多階段的收斂預測，達到逐步逼近預測結果、提高預測精度的目的；

2)探討了多種預測方法在基坑變形預測中的適用性和有效性，能有效增加預測結果的穩定性；

3)具有完善的預測結構，具有較強的魯棒性，并能根據后期增加的監測數據對預測系統進行實時更新，達到基坑變形的動態預測。

1.1.2 預測過程

預測模型流程如圖1所示，并將預測過程敘述如下：

1)由于基坑變形監測數據在收集過程中具有非等時距的特點，采用3次樣條插值對原始數據進行等距處理；

2)受環境、人為等因素的影響，基坑監測數據含有一定的誤差信息，使得基坑變形序列的規律性較差，采用多種小波去噪對基坑的變形數據進行去噪處理，將時間序列分離為趨勢項和誤差項；

3)采用多種優化的支持向量機模型對基坑變形的趨勢項進行預測，并以變異系數作為各預測模型的評價指標，且確定組合權值，實現趨勢項的綜合預測；

4)由于誤差項具有較多的誤差信息，隨機性較強，具有一定的混沌特征，采用混沌BP神經網絡對誤差項進行預測，進而實現基坑變形的綜合預測，以期達到期望精度。

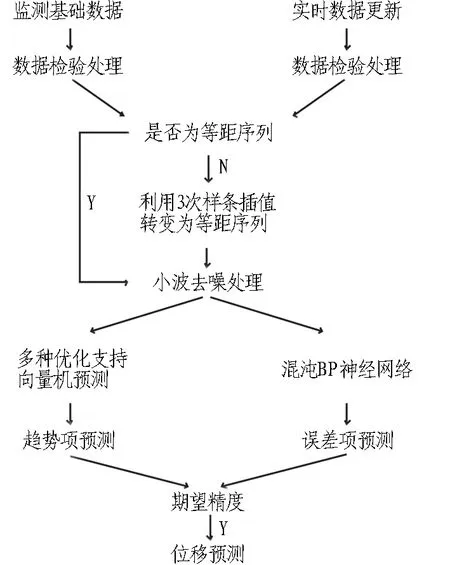
圖1 預測模型流程圖

1.2 小波去噪

基坑變形是多種因素的結合，包含了不同變形規律[8-10]，小波去噪能很好地將信噪進行分離，其基本思想是將誤差信息設定為白噪聲，并利用相關函數將信息分解為若干層高頻和低頻信息，且多以高頻信息為誤差信息、低頻信息為有用信息。將基坑變形的噪聲模型表示為

s(n)=f(n)+σ·e(n)。

(1)

式中：s(n)為原始監測數據；f(n)為趨勢項；σ為噪聲水平；e(n)為誤差信息；n為等間隔的時間。

在小波去噪過程中，小波函數、閾值類型及選取方式、分解層數等都對去噪效果有較大的影響，結合文獻[1]的研究，采用硬閾值的選取標準及啟發式閾值的選取方法，并探討db小波系和sym小波系在不同分解層數條件下的去噪效果。

另外，為評價不同小波去噪模型的去噪效果，以均方根誤差和信噪比為基礎評價指標，將兩者的歸一化累加值作為綜合評價指標。

1.2.1 均方根誤差

均方根誤差的表達式如下：

(2)

式中：RMSE為均方根誤差； f(i)為原始信號； f ′(i)為濾波后信號。

RMSE越小，說明去噪效果越好，保留的有用信息越多。

1.2.2 信噪比

信噪比的表達式如下：

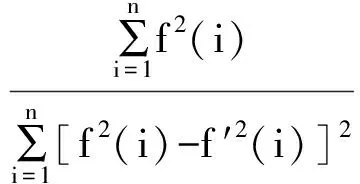
(3)

式中：SNR為信噪比指標； f(i)為原始信號； f ′(i)為濾波后信號。

SNR越大，說明去噪效果越優，剔除了更多的誤差信息。

均方根誤差和信噪比均能很好地評價去噪效果，為達到綜合評價的目的，對2個基礎指標進行歸一化處理，并將兩者的值進行疊加，進而得到綜合評價指標。

1.3支持向量機

支持向量機(SVM)[11-13]能利用內積函數將輸入信息投射到高維空間，進而實現非線性變換，具有較強的適應性及泛化能力，是目前預測研究中的熱點。若基坑的變形序列為{xn}，則可將支持向量機的線性函數表示為

y(x)=WTΦ(x)+b。

(4)

式中：y為對應節點的輸出信息；x為輸入信息；W為權值向量；Φ(x)為映射函數；b為偏置項。

在優化過程中，引入損失函數

(5)

其約束條件為：

(6)

上述的優化解可以通過對偶問題獲得，即：

(7)

其約束條件為：

(8)

式中ai、ai*為拉格朗日乘子。

通過二次規劃解決上述最優化問題，即可得到支持向量機的預測模型

(9)

式中： m為非零支持向量個數； K(x,xi)為核函數。

在支持向量機的應用過程中，核函數為徑向基核函數，且采用遞推預測結構，即輸入前5個相鄰監測數據，輸出緊鄰的預測樣本，以此類推進行訓練，而不同實例的訓練樣本根據具體情況而定；同時，相關參數的設定對預測結果具有較大的影響，即對使用者的經驗依賴較大，如正則項系數對預測結果的影響不可忽略，為提高預測模型的預測精度，采用最小二乘法和粒子群算法對支持向量機進行優化。

1.3.1 最小二乘法

該方法主要是將傳統支持向量機的不等式約束轉變為等式約束，且最小二乘法優化支持向量機還能將經驗風險項由1次轉化為2次，實現結構風險的調整。

1.3.2 粒子群算法

該方法具有較強的全局搜索能力，適用能力強，不需要進行太多的參數設定就能實現快速收斂，能有效地解決高維空間的非線性問題。其可以分解為2個搜索過程： 1)以加速遞減的方式來確定權重系數的閾值范圍； 2)以減速遞減的方式進行收斂，以求解權重系數的最優解。

1.4 混沌BP神經網絡

BP神經網絡是一種多層神經網絡，網絡層數多為3層，由輸入層、隱層及輸出層組成，其基于誤差反向傳播來實現誤差修正。在信息的傳播過程中，各層神經元之間是采用全連接的方式，而同層神經元之間則是無連接。BP神經網絡的學習過程是誤差修正的學習過程，主要分為正向傳播和反向傳播2個過程，其中正向傳播是輸入信號依次逐步傳播的過程，即下層神經元所包含的信息只受上層神經元的影響； 當輸出信息與期望精度不一致時，則會進入反向傳播過程，該過程則是通過修正各層神經元之間的連接權值，達到減小輸出誤差的目的[14-15]。

考慮到基坑變形序列的誤差項具有明顯的混沌特征，且BP神經網絡也具有收斂速度慢，易陷入局部最優解等缺點。采用混沌算法對BP神經網絡進行優化改進，該方法的思想主要是利用混沌變量線性映射到優化變量的閾值區間，再利用混沌原理進行全局搜索，達到全局優化的目的，其過程如下：

1)將混沌變量線性映射到優化變量的閾值區間，作為其初始值，實現神經網絡的初始值優化；

2)利用混沌變量進行全局的迭代搜索，并將搜索結果帶入到目標函數中；

3)在迭代過程中，若當前函數值為最優值，則停止迭代，否則將優化值替代當前函數值，再進入下一次迭代。

2 實例分析

為充分驗證本文預測模型的有效性和適用性，利用3個實例(均為深基坑實例)模型進行檢驗，其中2個作為可靠性驗證實例。

2.1 工程概況

實例1來源于文獻[8]，某基坑共有40個周期的沉降監測數據，每個監測周期是2d，相關數據詳見表1。由表1可知： 在監測周期內，基坑的沉降變形具有持續增加的特點，最大變形量已達24.84mm。

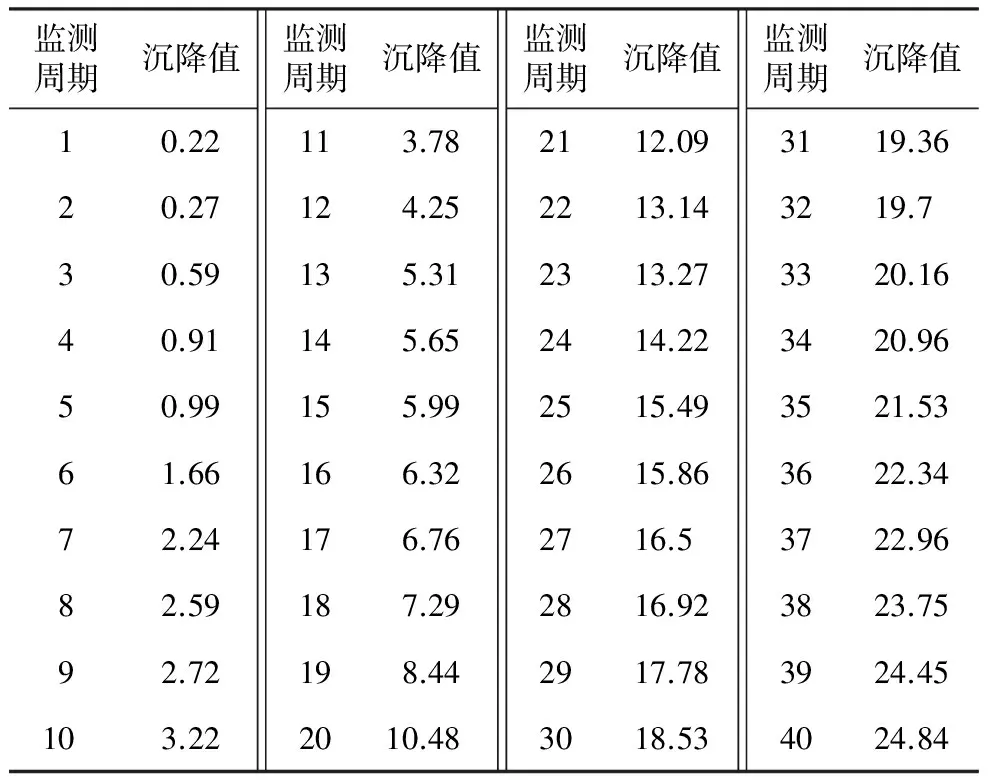
表1 基坑沉降變形數據統計

再進一步對基坑的變形速率特征進行統計分析，經統計得到基坑的最大沉降速率為2.04 mm/周期，最小沉降速率為0.05 mm/周期，平均沉降速率為0.62 mm/周期。以上述特征量為基礎，將其中間值作為分界指標，把基坑的變形速率劃分為4個區間： 低速變形區間(0.05～0.29 mm/周期)、一般變形區間(0.29～0.62 mm/周期)、緩加速變形區間(0.62～1.33 mm/周期)及加速變形區間(1.33～2.04 mm/周期)，各區間的分布比例如圖2所示。

圖2 基坑沉降速率變形區間分布

Fig. 2 Proportions of every deformation section in terms of defor- mation velocities

由圖2可知： 基坑變形速率呈現中間分布多、兩側分布少的特點，且以一般變形區間所占的比例最大，比例值為47.5%，而加速變形區間所占的比例最小，比例值為5%，說明基坑變形以持續的一般變形為主，現場施工的變形控制措施效果較好，基坑未出現較多的快速變形，達到了施工所期望的目標。

2.2 變形預測

2.2.1 小波去噪

依據預測思路，首先對基坑變形數據進行檢驗及去噪處理，在去噪過程中，討論了小波函數及分解層數對去噪效果的影響，結果如表2—4所示。

表2 小波函數去噪效果統計

由表2可知： 2個小波系的去噪效果差異較明顯，通過對比不同階次的去噪效果，得出高階次小波函數的去噪效果相對優于低階次小波函數的去噪效果，且2個小波系中均以6階次的去噪效果最優，db6小波系的評價值為1.643，sym6小波系的評價值為1.726，sym小波系更優。為進一步對比2個小波系的去噪效果，再對兩者的相關特征參數進行統計，結果如表3所示。

表3 小波系的特征參數統計

由表3可知： sym小波系在去噪效果及穩定性方面都優于db小波系，且sym小波系的變異系數值為0.309，小于db小波系的變異系數，說明db小波系的去噪結果具有更強的隨機性和波動性，而sym小波系的穩定性則相對更好。因此，選取sym6作為小波去噪的小波函數，并進一步探討分解層數對去噪結果的影響，詳見表4。

表4 小波去噪分解層數效果統計

由表4可知： 不同分解層數對去噪效果的影響也較大，其去噪效果主要表現為隨分解層數的增加，評價指標值先增加后減小，當分解層數為12時，評價指標值為1.756，去噪效果最優。因此，選取小波函數sym6在12層分解時的去噪結果作為基坑變形趨勢項和誤差項分離的依據。

2.2.2 趨勢項預測

采用多種優化的支持向量機模型對基坑變形的趨勢項序列進行預測，結果如表5所示。通過對比不同預測模型在不同節點的預測結果，得出不同模型預測結果的差異較顯著，說明不同預測模型具有不同的適用性。

表5 基坑變形趨勢項預測統計

鑒于表5中各預測方法的相對誤差具有正負的情況，對各預測結果的相對誤差進行絕對值處理后，再求解相應預測結果的相對誤差期望及方差。得到PSO-SVM模型預測結果的相對誤差期望及方差值分別為2.15%和0.462 7； LS-SVM模型預測結果的相對誤差期望及方差值分別為1.76%和0.229 7，后者的預測精度及穩定性相對更優。

為進一步對比不同預測結果之間的差異，對不同預測模型在不同節點的預測誤差進行統計，如圖3所示。

圖3 預測誤差對比

由圖3可知： 2種優化支持向量機模型的預測誤差都小于傳統支持向量機模型的預測誤差，其中，最大的預測誤差為0.84 mm，最小的預測誤差為-0.58 mm。各模型的預測誤差波動性均較大，規律性不強，說明預測誤差具有較強的波動性和隨機性。

另外，考慮到2個優化模型都不同程度地提高了預測精度，對2個模型的預測結果進行組合，實現趨勢項的綜合預測。對兩者變異系數進行統計，PSO-SVM模型的變異系數為0.215 6，LS-SVM模型的變異系數為0.130 5，前者大于后者，說明前者的預測結果具有相對更強的波動性，后者的預測結果更好。以變異系數為評價指標，確定2個模型的組合權值分別為0.377和0.623，組合預測結果如表6所示。對比單項預測結果，趨勢項的組合預測有效地提高了預測精度，達到了預期目標。

表6 趨勢項綜合預測結果

2.2.3 誤差項預測

由于誤差項序列具有非線性的混沌特征，采用混沌BP神經網絡對其進行預測，結果如表7所示。通過對預測結果的統計，得出誤差項預測結果的相對誤差均值為5.6%，明顯大于趨勢項的預測結果，這與誤差項含有更多的誤差信息有關，也說明了前文小波去噪分離趨勢項和誤差項的有效性。

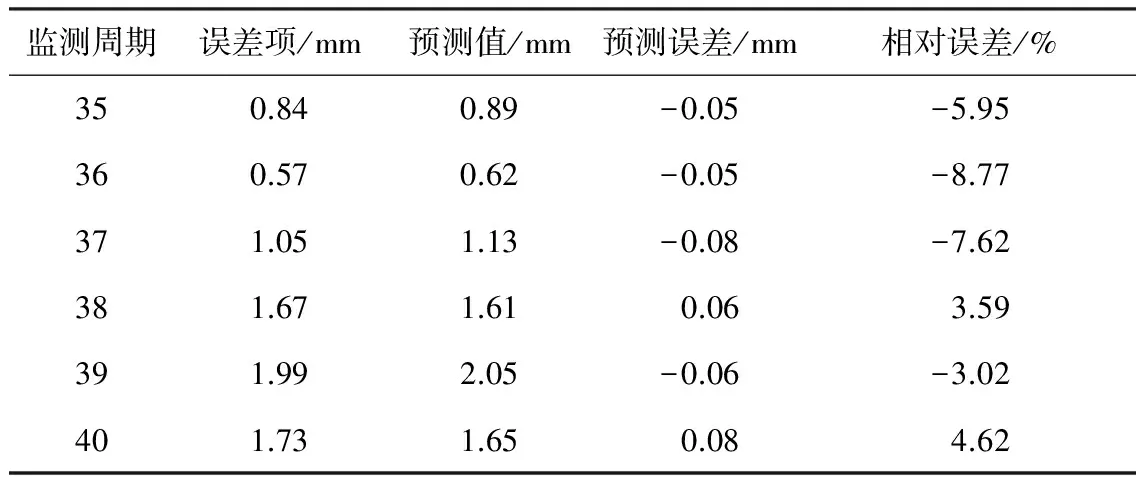
表7 基坑變形誤差項預測統計

由表6和表7得到基坑的變形預測結果如表8所示。由表8可知： 基坑變形預測結果的相對誤差最大值僅為1.44%，說明本文預測模型的預測精度較高，驗證了預測模型的有效性。同時，再對后4個周期的變形進行預測，得到基坑后4個周期的變形仍處于增長趨勢，為后期施工提供了一定的指導依據。

表8基坑變形綜合預測結果

Table 8 Comprehensive prediction results of foundation pit defor- mation

監測周期沉降值/mm趨勢項/mm誤差項/mm預測值/mm相對誤差/%3521．5320．610．8921．500．143622．3421．400．6222．021．443722．9621．871．1323．00-0．163823．7521．971．6123．580．733924．4522．502．0524．55-0．424024．8423．281．6524．93-0．354124．930．9725．904225．121．2126．334325．181．1426．324425．461．7427．20

2.3 可靠性驗證

為驗證預測模型的有效性，再利用其他實例對其進行驗證，考慮到上文的研究成果，在去噪部分，小波函數采用sym6，分解層數設定為12層。驗證實例共有2個，將其基本概況及預測結果分述如下。

2.3.1 實例2

某基坑[16]縱向長237.6 m，寬度為33.8 m，底板距地表20.8 m，圍護結構為地下連續墻，嵌入深度為19.5 m。同時，該基坑西側鄰近建筑物，為保證基坑安全及監控對周邊建筑物的影響，增設了沉降監測點，監測時間為2012年10月20日至2012年11月8日，共計20個周期，其變形數據如表9所示。

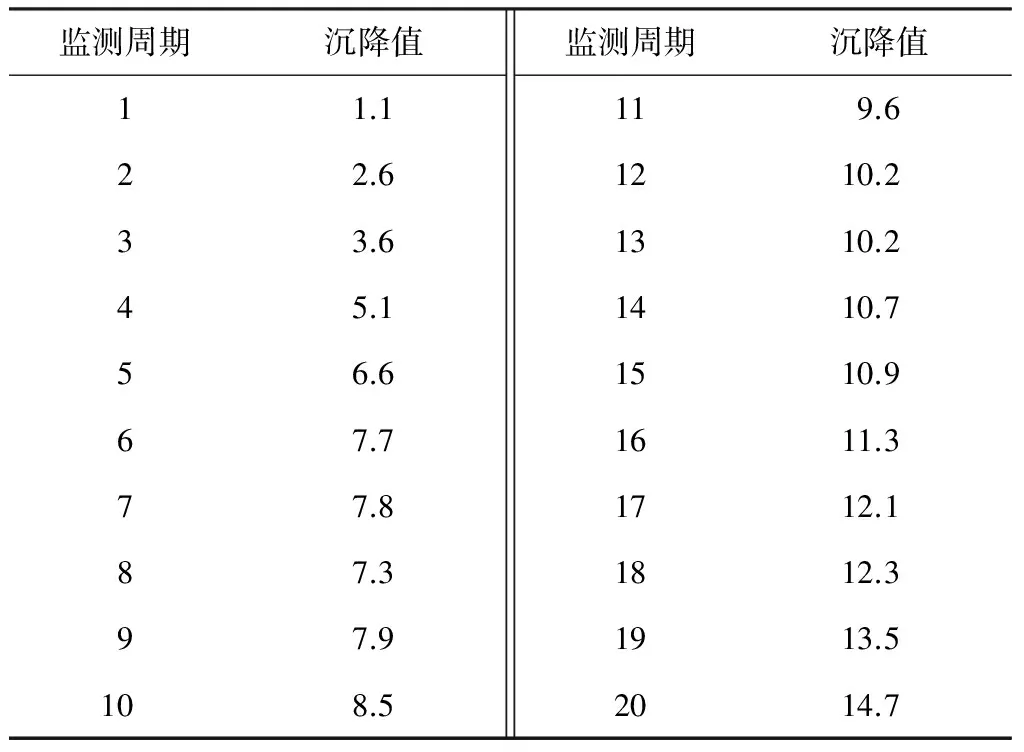
表9 實例2的變形數據

根據預測模型步驟進行預測，得到預測結果如表10所示。根據預測結果，在趨勢項的預測過程中，PSO-SVM模型的變異系數值為0.437 5，LS-SVM模型的變異系數值為0.149 1，前者具有更大的波動性，后者的預測結果相對更優； 通過計算得到兩者組合權值分別為0.254 2和0.745 8，經過組合計算，得到趨勢項的組合預測結果的相對誤差絕對值多是處于1%～3%，最大相對誤差僅為2.63%。在誤差項的預測過程中，預測誤差為-0.2～0.37 mm，預測誤差值較小，但相對誤差值較大。將趨勢項和誤差項的預測結果進行疊加得到基坑的變形預測值，預測結果的相對誤差多在0～2%，最大相對誤差為1.55%，預測精度較趨勢項預測的精度有所提高，說明通過分離預測的思路是可行的，能有效地提高預測精度。

2.3.2 實例3

某基坑[17]為高程建筑基坑，開挖深度達21.2 m，周邊地層條件較差，含有流砂層，且地下水豐富，加之工程規模大，施工過程將跨越雨季，進而導致施工難度大，合理監測對評價基坑的穩定性具有重要的意義。監測頻率為1～2次/d，為后期預測方便，以7 d為一周期進行統計，共得到15個周期，監測結果如表11所示。

表11 實例3的變形數據

實例3的預測結果如表12所示。該實例在趨勢項預測過程中，PSO-SVM模型的變異系數為0.332 5，而LS-SVM模型的變異系數為0.152 8，也是PSO-SVM模型的波動性更強，而LS-SVM模型具有更高的預測精度，與前兩者的預測結果具有較好的一致性； 通過計算得到組合權重為0.321 6和0.678 4，預測結果的相對誤差最大、最小值分別為2.96%和0.51%。在誤差項的預測過程中，預測誤差為-0.27～0.23 mm，預測誤差值不大，但也具有相對誤差大的特點。

通過對2個分離序列的預測，將其結果進行疊加，得到該實例的變形預測結果如表13所示。預測結果的最大相對誤差為2.74%，平均相對誤差為1.86%，方差為0.868 2，而文獻[17]中預測結果的相對誤差均值為6.14%，方差為1.049 2，得出預測結果較文獻[17]提高了3.31倍的預測精度及1.21倍的穩定性，驗證了預測模型的有效性。

2.4 實例預測結果對比

為進一步分析預測模型的有效性，再對3個實例預測結果的相對誤差均值及方差進行統計，結果如表14所示。

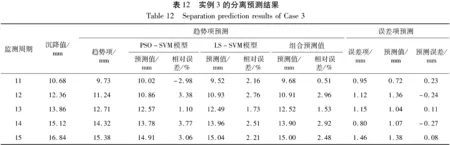
表13 實例3的預測結果

監測周期沉降值/mm分離預測結果趨勢項/mm誤差項/mm變形預測結果預測值/mm相對誤差/%文獻[17]預測結果預測值/mm相對誤差/%1110．689．680．7210．402．6111．275．521212．3610．911．3612．270．7512．954．761313．8612．521．0413．562．2014．867．211415．1213．901．0714．970．9816．066．221516．8415．001．3816．382．7418．027．01

表14 各實例相對誤差的參數統計

由表14可知： 3個實例的相對誤差期望值及方差值均較小，綜合驗證了預測模型的適用性及推廣性較強，對基坑的變形預測具有較好的效果。其中，在預測精度方面，實例1的預測精度最高，其次是實例2和3； 而在預測結果的穩定性方面，以實例2的穩定性最佳，其次是實例1和3。綜上所述，本文預測模型具有預測精度高、適用性強的特點。

3 結論與討論

1)通過對預測模型的結構優化，有效地增加了預測結果的穩定性，并能根據后期數據的不斷更新，實時調整預測參數，達到滾動預測的目的。預測模型能根據現場的實際情況預測基坑未來變形的發展趨勢，對指導和優化現場施工具有重要的意義。

2)在小波去噪的過程中，小波函數及分解層數對去噪效果的影響較大，經檢驗得到以sym6小波函數在12層小波分解時的去噪效果最優，并將其作為趨勢項及誤差項的分離依據。

3)通過對趨勢項和誤差項的預測可知，最小二乘法優化支持向量機模型的預測效果要優于粒子群優化支持向量機模型的預測效果，前者的預測精度及穩定性相對更高，并通過組合預測進一步提高了趨勢項的預測精度，且趨勢項的預測結果也要優于誤差項的預測結果，這與誤差項含有較多的誤差信息有關。

4)預測模型具有理論簡單、預測精度高和方法簡單可行等優點，可對其在其他巖土領域的變形預測效果進行可行性研究。本文僅研究了支持向量機及BP神經網絡進行組合的效果，未對其他預測方法的適用性進行研究，下一步考慮對其進一步探討。

[1] 楊哲峰, 羅林, 賈東彥, 等. 基于小波去噪的深基坑變形預測研究[J]. 人民長江, 2014, 45(19): 41. YANG Zhefeng, LUO Lin, JIA Dongyan, et al. Prediction of deep foundation pit deformation based on wavelet de-noising[J]. Yangtze River, 2014, 45(19): 41.

[2] 姜彥作, 周杰, 沈壽亮, 等. 基于LS-SVM—馬爾科夫模型的大壩變形預測[J]. 水電能源科學, 2014, 32(3): 103. JIANG Yanzuo, ZHOU Jie, SHEN Shouliang, et al. Dam deformation prediction based on LS-SVM-Markov model[J]. Water Resources and Power, 2014, 32(3): 103.

[3] 曹凈, 丁文云, 趙黨書, 等. 基于LSSVM-ARMA模型的基坑變形時間序列預測[J]. 巖土力學, 2014, 35(增刊2): 579. CAO Jing, DING Wenyun, ZHAO Dangshu, et al. Time series forecast of foundation pit deformation based on LSSVM-ARMA model [J]. Rock and Soil Mechanics, 2014, 35(S2): 579.

[4] 林楠, 李偉東, 張文春, 等. 最小二乘支持向量機在深基坑變形預測中的應用[J]. 遼寧工程技術大學學報(自然科學版), 2014, 33(11): 1471. LIN Nan, LI Weidong, ZHANG Wenchun, et al. Deformation prediction of deep foundation pit with least square support vector machine[J]. Journal of Liaoning Technical University (Natural Science), 2014, 33(11): 1471.

[5] 曹凈, 丁文云, 趙黨書, 等. 基于PSO-LSSVM模型的基坑變形時間序列預測[J]. 控制工程, 2015, 22(3): 475. CAO Jing, DING Wenyun, ZHAO Dangshu, et al. Time series forecast of foundation pit deformation based on PSO-LSSVM [J]. Control Engineering of China, 2015, 22(3): 475.

[6] 彭磊, 黃張裕, 凌晨陽, 等. 基于PSO-SVM模型的深基坑變形預測研究[J]. 工程勘察, 2011, 39(3): 82. PENG Lei, HUANG Zhangyu, LING Chenyang, et al. Research on deformation prediction of deep foundation pit based on PSO-SVM model[J].Geotechnical Investigation and Surveying, 2011, 39(3): 82.

[7] 王江, 袁寶遠, 任麗芳, 等. 新型智能算法在基坑變形監測中的應用[J]. 中外公路, 2007, 27(1): 23. WANG Jiang, YUAN Baoyuan, REN Lifang, et al. Application of new intelligent algorithm in foundation pit deformation monitoring[J]. Journal of Chinese and Foreign Highway, 2007, 27(1): 23.

[8] 冉岸綠, 李明廣, 陳錦劍, 等. 共用地下連續墻深基坑影響下地鐵車站與隧道節點變形分析[J]. 隧道建設, 2016, 36(7): 844. RAN Anlü, LI Mingguang,CHEN Jinjian, et al. Deformation behaviors of joint between shield tunnel and underground station impacted by connected deep foundation pit[J]. Tunnel Construction, 2016, 36(7): 844.

[9] 陳澤昌, 毛堅強, 劉建國. 成都某地鐵車站排樁支護結構受力變形規律研究[J]. 隧道建設, 2012, 32(3): 309. CHEN Zechang, MAO Jianqiang, LIU Jianguo. Research on displacement and stress of soldier pile structure in foundation pit of metro station in Chengdu[J]. Tunnel Construction, 2012, 32(3): 309.

[10] 霍曉波, 廖少明. 武漢I級階地某地鐵深基坑支護優化及實測分析[J]. 隧道建設, 2016, 36(1): 71. HUO Xiaobo, LIAO Shaoming. Analysis of optimization and monitoring of supporting structure of a deep metro station pit in first terrace of Yangtze River in Wuhan,China[J]. Tunnel Construction, 2016, 36(1): 71.

[11] 李宏輝. 基于LS-SVM的基坑周邊地表沉降預測模型[J]. 南寧職業技術學院學報, 2013, 18(4): 89. LI Honghui. LS-SVM-based forecasting models for ground settlement of foundationpit[J]. Journal of Nanning Polytechnic Institute, 2013, 18(4): 89.

[12] 吳歡, 周春波, 秦昆. 基于改進支持向量機的深基坑變形預測[J]. 地礦測繪, 2015, 31(4): 25. WU Huan, ZHOU Chunbo, QIN Kun. Deformation prediction of deep foundation pit based on improved support vector machine [J]. Surveying and Mapping of Geology and Mineral Resources, 2015, 31(4): 25.

[13] 劉賀, 張弘強, 劉斌. 基于粒子群優化神經網絡算法的深基坑變形預測方法[J]. 吉林大學學報(地球科學版), 2014, 44(5): 1609. LIU He, ZHANG Hongqiang, LIU Bin. A prediction method for the deformation of deep foundation pit based on the particle swarm optimization neural network[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(5): 1609.

[14] 賈備, 鄔亮. 基于灰色BP神經網絡組合模型的基坑變形預測研究[J]. 隧道建設, 2009, 29(3): 280. JIA Bei, WU Liang. Research of the prediction of foundation deformation based on gray BP neural network combined model[J]. Tunnel Construction, 2009, 29(3): 280.

[15] 楊愛婷, 高正夏, 卞志兵, 等. 基于時間序列ACO-BP神經網絡在基坑變形預測中的應用研究[J]. 路基工程, 2015(2): 58. YANG Aiting, GAO Zhengxia， BIAN Zhibing, et al. Study of application of time sequence based ACO-BP neural network in prediction of foundation pit deformation[J].Subgrade Engineering， 2015(2): 58.

[16] 王興. 幾種常用基坑變形預測模型的比較與分析[J]. 山西大同大學學報(自然科學版), 2016, 32(1): 62. WANG Xing. The comparison and analysis of several deformation forecast models of pit[J]. Journal of Shanxi Datong University (Natural Science), 2016, 32(1): 62.

[17] 代春泉, 王磊. 深基坑施工變形預測VAR建模與應用分析[J]. 巖土力學, 2012, 33(增刊2): 395. DAI Chunquan, WANG Lei. VAR modeling of construction deformation prediction of deep foundation pit and application[J]. Rock and Soil Mechanics, 2012, 33(S2): 395.

StudyofDeformationPredictionofFoundationPitBasedonOptimizedSupportVectorMachineandChaoticBPNeuralNetwork

WANG Xingke, WANG Juan

(ShaanxiRailwayInstitute,Weinan714000,Shaanxi,China)

U 452

A

1672-741X(2017)09-1105-09

2016-12-02;

2017-03-27

王興科(1982—)，男，河北石家莊人，2013年畢業于蘭州交通大學，巖土工程專業，碩士，講師，主要從事土木工程教學與研究工作。E-mail: 524980530@qq.com。

10.3973/j.issn.1672-741X.2017.09.007