離心泵葉片表面布置障礙物抑制空化的數值模擬與實驗

趙偉國 趙國壽 咸麗霞 韓向東

(1.蘭州理工大學能源與動力工程學院， 蘭州 730050; 2.蘭州理工大學甘肅省流體機械及系統重點實驗室， 蘭州 730050)

離心泵葉片表面布置障礙物抑制空化的數值模擬與實驗

趙偉國1,2趙國壽1咸麗霞1韓向東1

(1.蘭州理工大學能源與動力工程學院， 蘭州 730050; 2.蘭州理工大學甘肅省流體機械及系統重點實驗室， 蘭州 730050)

以一臺比轉數為32的低比轉數離心泵作為研究模型，提出了一種在葉片工作面加障礙物的方法來抑制空化初生及發展的方法。在不同空化數下，采用修正的SSTk-ω湍流模型和Kubota空化模型對模型泵葉片表面在有、無障礙物條件下進行三維非定常數值模擬，結果表明：低比轉數離心泵在有障礙物運行時揚程下降在5%以內，效率下降在3%以內，設計點揚程下降3%，效率下降1.2%。障礙物可以有效增大葉片近壁湍動能，改變壓力分布，對離心泵內各個階段空化均有抑制作用。障礙物可以優化流場結構，削弱靠近葉片背面的旋渦強度，對靠近隔舌區域的葉片工作面和背面作用效果明顯。有障礙物時離心泵葉輪內空泡體積在空化各個階段均小于無障礙物時葉輪內空泡體積，在空化發展階段，障礙物使空泡體積持續衰減。空泡尺度發展到障礙物位置時，障礙物可以較大程度減低壓力脈動主頻幅值，對流場優化產生最佳效果，在空化發展其他階段，障礙物會對葉輪內壓力脈動造成小幅擾動。

離心泵； 障礙物； 空化抑制； 數值模擬

引言

離心泵是應用最廣泛的流體機械之一， 其中低比轉數離心泵一直存在效率不高、汽蝕性能較差、內部流動不穩定等問題。空化是離心泵運行時常見的一種物理現象，離心泵在運行時產生的回流與空化流動相互作用，形成對葉輪內能量交換更為復雜的干擾和破壞[1]。空化不僅對定常態的流體流動產生影響，還會影響流動的非定常特性或動態響應特性。動態響應的改變會使流動內部出現不穩定性，對外表現為離心泵的振動和噪聲特性。離心泵內部空化表現為旋轉空化[2-3]、空化喘振[1,4]、堵塞喘振及其他一些高頻流動不穩定性[5]。在離心泵空化狀態由空化初生工況到揚程斷裂工況的發展過程中，空泡在葉輪流道內積累并逐漸影響葉輪內正常的能量交換。空化是包含相變、非定常、多維湍流等多種復雜影響因素的流動現象，流體機械內部的空化流動嚴重影響機器性能，其非定常脫落更是引起機器振動、噪聲和磨蝕等嚴重問題[5]。離心泵內空化現象通常發生在葉片前緣，在低流量工況時，在葉片吸力面發生空化，高流量時在壓力面發生空化。在工程應用中，常以凈正吸頭、空化數和吸入比轉數等來表征離心泵的工作條件和吸入性能[1]。對于空化的數值模擬已成為目前研究的重要手段。

圖1 計算域網格與監測點Fig.1 Grid of computational domain and monitoring points

目前抑制空化的方法主要有3種：在葉片空化面布置障礙物阻擋回射流、設置反向空氣射流[6]、使用開縫葉片優化流場結構[7]。KAWANAMI等[8]通過一系列水翼實驗觀察到片空化的破裂是由翼型尾部向頭部流動的回射流引起的，并指出在片空化末端即翼型中部設置小的障礙物阻擋回射流，可以預防空化的產生。戴月進等[9]在翼型表面施加粗糙帶，增加了近壁面流場湍動能，使轉捩提前，提高了近壁面流場壓力，抑制空化初生的發生。牟介剛等[10]分析了非光滑表面離心泵葉輪的流動減阻特性。司喬瑞等[11]采用 SSTk-ω湍流模型分析了空化條件下離心泵泵腔內不穩定流動。盧加興等[12]基于模擬和實驗研究了空化條件下泵進出口的壓力頻率特性。付燕霞等[13]數值模擬了離心泵葉片入口處的回流旋渦空化。MEDVITZ等[14]基于Kunz空化模型[15]研究了小空化數下離心泵內空化流動。TAN等[16]基于修正的RNGk-ε湍流模型[17]模擬了離心泵小流量工況下運行時的壓力脈動特性。

本文在前人研究工作的基礎上，基于修正的SSTk-ω湍流模型[18]和Kubota空化模型[19]，通過對比離心泵葉片工作面布置障礙物發生空化的形式、形成過程、空化團的非對稱分布及其與壓力脈動之間的關系，采用瞬態模擬方法，分析障礙物對空泡流動的抑制作用，以期為抑制空化和離心泵的優化設計提供參考。

1 計算模型與網格劃分

計算模型為一比轉數為32的低比轉數離心泵，設計參數為：流量Q=8.6 m3/h，揚程H=4.2 m，轉速n=500 r/min。葉片形狀為圓柱葉片，主要幾何參數如下：泵入口直徑Ds=90 mm，泵出口直徑Dd=65 mm，葉輪入口直徑D1=80 mm，葉輪出口直徑D2=310 mm，葉輪出口寬度b2=12 mm，葉片進口角β1=37°，葉片出口角β2=37°，葉片數Z=6。

對葉輪流道內進行六面體網格劃分，以便準確捕捉障礙物凸起對周圍流場的影響，蝸殼采用適應性較強的四面體網格，整體計算域如圖1a所示。網格無關性檢查如表1所示，隨著網格數增大，揚程逐漸趨于穩定，最終確定網格單元數1 017 321，節點數838 520。為保證數值模擬精度，常用Y+值來保證近壁面區域有足夠的節點數來捕捉邊界層內的流動[20]，文中Y+表示離壁面最近的網格點到壁面的距離，為無量綱變量，定義為

式中τω——壁面切應力，Paρ——流體密度，kg/m3Δn——離壁面最近2個網格點間距離，mυ——運動粘度，m2/s

表1 網格無關性檢查Tab.1 Check of grid independence

本文所采用的SSTk-ω模型近壁區應用k-ω模型，考慮到邊界層網格的Y+值范圍，Y+在100左右基本滿足k-ω湍流模型對近壁網格質量要求[21]。本次模擬近壁網格Y+值能夠保證在離心泵流場模擬中具有較好的適用性。

葉輪流道內及隔舌監測點位置如圖1b所示，P1、P2、P3位于葉輪流道內，P5位于流道內障礙物前側，流道內點P1、P2、P3及P5均隨葉輪旋轉，P4點位于蝸殼隔舌處，不隨葉輪旋轉。結合前人對水翼表面障礙物的形狀位置研究[9-10,22]以及離心泵空化流場的觀測，障礙物布置在葉輪半徑45%處，障礙物截面形狀為2 mm×2 mm矩形，高度取6 mm，如圖2所示。

圖2 障礙物網格劃分Fig.2 Grid generation of obstacle

2 湍流模型和空化模型

汽液兩相采用ANSYS-CFX中的均相模型，即汽液兩相有相同的壓力場與速度場，兩相間無速度滑移，假定汽相在液相中均勻分布，混合相密度可變，混合相控制方程如下：

連續性方程

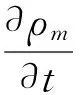
(1)

動量方程

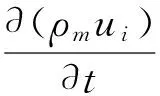
(2)

式中ui、uj、uk——速度分量ρm——混合相密度δij——克羅內克常數μ——層流粘度μt——湍流粘度t——時間xi、xj、xk——坐標分量p——壓力

N-S方程通過SSTk-ω湍流模型封閉。混合相密度可以表示為

ρm=αvρv+ρl(1-αv)

(3)

式中ρv、ρl——汽相和液相密度αv——汽相體積分數

2.1修正的SSTk-ω湍流模型

由MENTER[23]發展的SSTk-ω模型考慮到了湍流剪應力的傳輸，不但能對各種來流進行準確預測，還能在各種壓力梯度下精確地模擬分離現象，綜合了k-ω模型在近壁模擬和k-ε模型在外部區域計算的優點，這是由于SSTk-ω模型比標準k-ω模型中多了一個混合方程，這個混合方程的作用是在近壁區域激活了標準k-ω模型，在遠場區域激活使用k-ε模型，而且SSTk-ω使用了修正的湍流黏度來考慮湍流剪應力的傳輸，且較標準k-ω模型，SSTk-ω模型的ω方程中多了一個交叉擴散項D，這些改進使SSTk-ω模型比標準k-ω模型在廣泛的流動領域中有更高的精度和可信度。尤其適合低比轉數離心泵內高旋轉、大曲率變形的流動。其控制方程為

(4)

(5)

(6)

式中Gk——湍動能k的生成項Gω——耗散率ω的生成項Γk、Γω——k和ω的有效擴散系數Yk、Yω——由于紊流引起的k和ω的耗散Dω——交叉擴散項Sk、Sω——用戶自定義的源項

由于空化流具有密度可變、兩相之間密度比較大的特點，因此空化流的數值模擬主要困難在于處理汽液相變而造成的密度變化。特別是空化區域，密度急劇變化，采用常規的SSTk-ω湍流模型會過大地預測流道內近葉片表面的流體黏性，從而導致云空化泡難以脫落，因此需要對SSTk-ω模型湍流粘度進行修正，以便更好地捕捉模擬離心泵內空泡流的動態特性。本文僅對式(2)中的黏性項進行修正，應用密度函數f(ρ)替代式(6)中的混合密度，故計算湍流黏度的公式為

(7)

其中

(8)

對于式(8)中n的取值一般建議取10。引入密度函數后，特別是對水蒸氣含量較小的氣液混合區域，可以限制空穴尾部水氣混合區過大的湍流度，以更好地模擬離心泵內非穩態空泡脫落行為[24]。

2.2 Kubota空化模型

Kubota空化模型由簡化Rayleigh-Plesset方程發展而來，忽略了空泡半徑隨時間的二階導數[25]，重點考慮了空化初生和發展時空泡體積變化的影響，適于模擬離心泵云空化的非定常特性。Kubota空化模型是基于輸運方程，即

式中fv——汽相質量分數Re——液相蒸發速率Rc——汽相凝結速率Rb——簡化汽泡半徑pv——飽和蒸汽壓力αnuc——氣核體積分數Ce、Cc——蒸發和凝結經驗系數

前人研究經工作驗證[26]，上述經驗系數的合理取值為：Rb=1×10-6m；αnuc=5×10-4；Ce=50；Cc=0.01。

3 邊界條件給定

采用商用代碼ANSYS CFX 15.0全隱式耦合技術對方程組進行求解，修改的SSTk-ω湍流模型通過CFX二次開發嵌入程序，計算模型邊界條件為入口設置成總壓進口，出口設置成質量流量出口，系統參考壓力設置為0 Pa，空化臨界壓力取常溫下(25℃)純水飽和蒸汽壓力(3 169 Pa)，固壁面邊界設置成無滑移壁面。

定常計算中動靜交界面設置為凍結轉子，將收斂的定常計算結果作為非定常計算的初始場，非定常計算中動靜交界面設置為瞬態凍結轉子，時間步長Δt取0.001 s，即葉輪每旋轉3°為1個時間步長，總計算步數為240步，即葉輪旋轉2圈，并取第2個旋轉周期的計算結果進行非定常特性分析。求解過程中控制方程的對流離散型采用二階高精度格式，時間項離散格式為二階后向歐拉差分格式，庫朗數下限設為0.5，上限設為1以加快每一時間步數的收斂，將最大殘差作為求解收斂的判別標準，收斂精度設置為10-4。

本次計算通過降低進口壓力使離心泵流道內發生空化，比較有、無障礙物時的內部空化形態，以及對流場壓力脈動的影響，分析其抑制效果與機理。

4 計算結果與分析

4.1 外特性實驗對比

為了驗證數值模擬的準確性，在蘭州理工大學離心泵閉式實驗臺上進行離心泵外特性實驗，圖3(圖中Q0表示設計流量)為不同流量工況下葉片有、無障礙物性能模擬值與實驗值對比曲線。

圖3 外特性曲線Fig.3 Curves of external performance

在流體機械領域，常用無量綱空化數σ表述空化發生的可能性，其定義為

其中

式中p1——基準靜壓力，采用泵進口壓力，PaU——基準速度，采用葉輪葉片進口邊與前蓋板交點處的圓周速度，m/s

n——軸轉速，r/min

D1——葉輪葉片進口邊與前蓋板交點處的直徑，m

圖4為葉片在有、無障礙物條件下空化數σ與揚程的計算結果對比曲線。

圖4 汽蝕特性曲線Fig.4 Curves of cavitation performance

圖3可以看出無障礙物時模擬值與實驗值吻合較好，與模擬值比較，增加障礙物后揚程下降在5%以內，對效率影響較小，下降在3%以內。設計點揚程相差3%，效率相差1.2%。

由圖4可以看出增加障礙物后對揚程的影響，對空化初生無明顯影響，揚程斷裂時，無障礙物時H=2.60 m，有障礙物時H=3.71 m，提高29.7%，抑制效果明顯。

4.2 障礙物對湍動能分布影響

圖5為不同空化數下，葉輪中間截面湍動能等值線圖，上圖為不加障礙物時湍動能分布，下圖為加障礙物時湍動能分布。

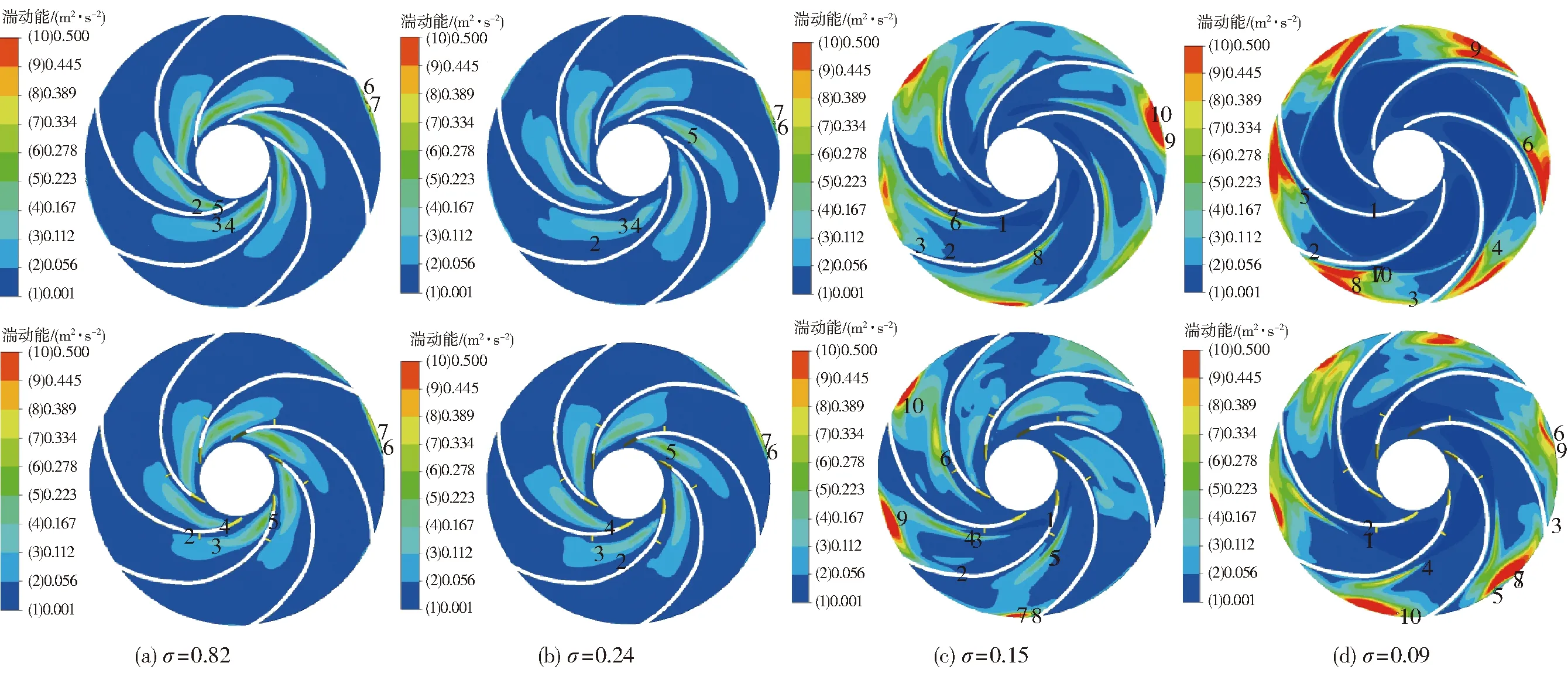
圖5 湍動能分布Fig.5 Turbulence kinetic energy distributions

圖6 絕對壓力分布Fig.6 Absolute pressure distributions

湍流流動具有動量大且傳遞快的特點。葉片表面障礙物能夠增加近壁面流場湍動能，從而使轉捩提前發生，減少分離引起的壓差阻力，使壓力梯度變大，從而對空化產生抑制作用。如圖5a所示，障礙物對空化初生湍動能分布無明顯影響。當空化發展到一定長度，障礙物前后壁面湍動能影響顯著增大，如圖5b、5c所示。空化完全發展時，障礙物對湍動能的影響趨向最大化，抑制效果最明顯，如圖5d所示。

4.3 障礙物對壓力分布影響

圖6為不同空化數下，葉輪中間截面絕對壓力等值線圖，上圖為不加障礙物時壓力分布，下圖為加障礙物時壓力分布。

空化發生時，低壓區向葉輪出口擴張是使離心泵內空化發展的主因。葉片表面障礙物誘發了葉片表面附近相對高壓區和較大的逆壓梯度，壓力分布的變化會導致空泡形態的改變，因此加障礙物以后引起的壓力和壓力梯度的變化是產生抑制作用的重要因素。障礙物對空化初生的壓力分布無明顯影響，如圖6a所示。空化發展時，障礙物使流道內逆壓梯度增大，在葉片工作面障礙物附近形成了相對高壓區域，有效阻止了低壓區域向外擴張，如圖6b～6d所示。

4.4 障礙物對流場結構影響

圖7為不同空化數下，空泡在最終時刻的體積分數(αv=10%)等值面及中間截面流線在有、無障礙物時的比較，左側為無障礙物時流場圖，右側為有障礙物時流場圖。

如圖7a所示，空化初生時，障礙物可以優化流場結構，削弱靠近葉片背面的漩渦強度，對靠近隔舌區域的葉片工作面和背面作用效果明顯，對空泡形態并無較大影響。圖7b為空化發展時，空泡形態呈現出云空化的脫落特征，障礙物梳理了空化發展時的紊亂流場，削弱漩渦強度使流場更具流線型，無障礙物時空泡具有脫落特征，障礙物有效抑制了空泡的脫落。圖7c、7d顯示當空泡徑向尺度發展到障礙物位置時，由障礙物誘發的高壓區和增大的湍動能共同作用導致了空泡形態的變化。

圖7 空泡形態及流線Fig.7 Cavity patterns and streamlines

4.5 障礙物對空泡體積影響

葉輪內空泡體積Vcav定義為

空泡體積增長速度Ve定義為

式中N——葉輪內總控制單元數αv，i——每個控制單元內汽相體積分數Vi——每個控制單元體積，mm3

在一個葉輪旋轉周期內，空泡體積及體積增長隨時間變化如圖8所示。

圖8 空泡體積與空泡體積增長速度圖Fig.8 Diagrams of cavity volume and its growth rate

由圖8a可知空化數σ=0.82時，加障礙物后在整個旋轉周期內汽泡體積明顯減小，增長和衰減交替變化，體積增減趨勢有無障礙物基本一致。由圖8b可知空化數σ=0.24時，兩種情況體積均表現出先衰減后增長趨勢，衰減階段有障礙物流道空泡體積均小于無障礙物時空泡體積，有障礙物空泡體積變化速度相較無障礙物更為穩定。 由圖8c可知空化數σ=0.15時，加障礙物后空泡體積在整個周期內都小于無障礙物時的空泡體積，體積均呈現衰減趨勢且有障礙物時衰減速度更快。由圖8d可知空化數σ=0.09時，加障礙物后空泡體積在整個周期內都小于無障礙物時的空泡體積，無障礙物時，空泡體積穩定增長，有障礙物時空泡體積持續衰減。由障礙物誘發的葉片壁面附近相對高壓區和增大的湍動能共同作用抑制了葉輪內空泡體積的增長。

4.6 障礙物對內部流動瞬態特性影響

障礙物的存在對流場內部造成了擾動，影響了流動的瞬態特性，圖9為對流道內部及隔舌處監測點壓力脈動做快速傅里葉變換，從壓力頻譜角度分析障礙物對內部流動瞬態特性影響。圖10為各個監測點在有、無障礙物時的主頻幅值比較。

圖9 壓力頻譜Fig.9 Pressure frequency spectra

圖10 壓力主頻幅值Fig.10 Amplitudes of dominate frequency of pressure

圖9為壓力脈動時域數據通過快速傅里葉變換得到的壓力脈動頻域分布圖。本文中葉輪轉速n=500 r/min，軸頻為8.3 Hz，葉輪葉片數z=6，則葉片通過頻率(即葉頻)為50 Hz。從圖9中可以看出，脈動主頻為50 Hz，障礙物并不改變在不同空化數下不同位置處的壓力脈動頻率分布。圖10顯示障礙物對不同空化數的主頻幅值影響，如圖10a、10b所示，在空化初生及發展階段，障礙物對流場造成了擾動，壓力脈動頻率有較小幅度增大；如圖10c所示，障礙物使流道內和隔舌處的壓力脈動幅值均有明顯減低作用，當空泡尺度發展到障礙物位置時(圖7c)，障礙物既可以起到抑制空化效果，同時降低壓力脈動主頻幅值，可以對空化流誘發的振動、噪聲、磨損等產生抑制作用，對流場優化產生最佳效果；圖10d中有障礙物時的主頻幅值略大于無障礙物時主頻幅值，此時空泡完全發展，如圖7d所示附著整個流道，空泡區形成了較為穩定的區域，空泡徑向尺度遠大于障礙物徑向位置，障礙物的存在會使高壓區向流道內部區域擴張，使空泡潰滅，起到抑制空化的效果，但是壓力脈動變得較為劇烈。

5 結論

(1)葉片表面加障礙物后，會使離心泵在各個工況下揚程有所降低，降低在5%以內，效率降低在3%以內，在設計點揚程下降3%，效率下降1.2%。發生空化時，對空化初生揚程無較大影響，相同空化數下，對斷裂點揚程影響較大，提高近30%，對于在空化狀態下運行的離心泵具有重要意義。

(2)對于空化初生及發展階段，障礙物對靠近葉片背面的漩渦強度削弱作用明顯，可以對云空泡脫落起到明顯的抑制作用，空泡徑向發展到障礙物位置后，障礙物引起的周圍流場高壓區和增大的湍動能抑制了空泡增長。

(3)在一個旋轉周期內，對于空化初生階段，障礙物使空泡體積明顯減小，空泡發展階段，障礙物減小空泡體積的同時使空泡體積以更快的速度衰減，空泡完全發展階段，無障礙物時，空泡體積穩定增長，有障礙物時，空泡體積持續衰減。

(4)空化初生階段，障礙物抑制空化的同時，會對流場造成擾動，增強流道內及隔舌處壓力脈動主頻幅值，增幅較小；當空泡徑向發展到障礙物位置時，抑制空化的同時減低壓力脈動主頻幅值，可以有效抑制空化流動誘發的流場非定常特性，效果最優；空泡完全發展時，障礙物抑制效果明顯，對流場的擾動使壓力脈動主頻幅值變大。

1 BRENNEN C E. Hydrodynamics of pumps[M]. Norwich，VT，USA: Concepts ETI Inc., 1994.

2 FRIEDRICHS J，KOSYNA G. Rotating cavitation in a centrifugal pimp impeller of low specific speed[J]. ASME Journal of Fluids Engineering，2002，124(12):356-362.

3 FRIEDRICHS J，KOSYNA G. Unsteady PIV flow field analysis of a centrifugal pump impeller under rotating cavitation[C]∥Proceedings of the 5th International Symposium on Cavitation，2003.

4 TSUJIMOTO Y，HORIGUCHI H，YONEZAWA K. Cavitation instabilities in cavitating and non-cavitating pumps[J]. Design and Analysis of High Speed Pumps，2006, 7(1): 7-24.

5 BRENNENC E. Multifrequency instability of cavitating inducers[J]. ASME Journal of Fluids Engineering，2007，129(6):731-736.

6 KUIPER G. New developments and propeller design [J]. Journal of Hydrodynamics，2010，22(9):7-16.

7 王洋，謝山峰，王維軍，等. 開縫葉片低比轉數離心泵空化性能的數值模擬[J]. 排灌機械工程學報，2016，34(3): 210-215. WANG Yang，XIE Shanfeng，WANG Weijun, et al. Numerical simulation of cavitation performance of low specific speed centrifugal pump with slotted blades[J]．Journal of Drainage and Irrigation Machinery Engineering，2016，34(3): 210-215．(in Chinese)

8 KAWANAMI Y，KATO H，YAMAGUHIH H，et al. Mechanism and control of cloud cavitation[J]. ASME Journal of Fluids Engineering，1997，119(4): 788-794.

9 戴月進，張媛媛，黃典貴．水翼表面粗糙帶對空化抑制效果的數值研究[J]．工程熱物理學報，2012，33(5):770-773. DAI Yuejin，ZHANG Yuanyuan，HUANG Diangui. Numerical study of the impact of hydrofoil surface roughness on cavitation suppression[J]. Journal of Engineering Thermophysics，2012，33(5):770-773.(in Chinese)

10 牟介剛，代東順，谷云慶，等. 非光滑表面離心泵葉輪的流動減阻特性[J].上海交通大學學報, 2016，50(2):6-12. MOU Jiegang，DAI Dongshun，GU Yunqing，et al. Characteristics of non-smooth surface drag reduction influence on centrifugal pump impeller[J]. Journal of Shanghai Jiao Tong University, 2016,50(2):6-12.(in Chinese)

11 司喬瑞，袁壽其，李曉俊，等. 空化條件下離心泵泵腔內不穩定流動數值分析[J/OL]. 農業機械學報，2014，45(5):84-90. http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20140513&flag=1. DOI:10.6041/j.issn.1000-1298.2014.05.013. SI Qiaorui，YUAN Shouqi，LI Xiaojun，et al. Numerical simulation of unsteady cavitation flow in the casing of a centrifugal pump[J/OL]. Transactions of the Chinese Society for Agricultural Machinery，2014，45(5):84-90.(in Chinese)

12 盧加興，袁壽其，任旭東，等. 離心泵小流量工況不穩定空化特性研究[J/OL]. 農業機械學報，2015，46(8):54-58. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150809&flag=1. DOI:10.6041/j.issn.1000-1298.2015.08.009. LU Jiaxing，YUAN Shouqi，REN Xudong，et al. Investigation of instabilities of cavitation at low flow rate of centrifugal pump[J/OL]. Transactions of the Chinese Society of Agricultural Machinery，2015，46(8):54-58.(in Chinese)

13 付燕霞，沈陳棟，袁建平，等. 離心泵進口回流誘導的空化特性[J]． 排灌機械工程學報，2016, 34(10): 841-846． FU Yanxia，SHEN Chendong，YUAN Jianping，et al．Cavitation characteristic induced by inlet backflow in a centrifugal pump[J]．Journal of Drainage and Irrigation Machinery Engineering，2016，34(10): 841-846．(in Chinese)

14 MEDVITZ R B，KUNZ R F，BOGER D A，et al. Performance analysis of cavitating flow in centrifugal pumps using multiphase CFD[J]. ASME Journal of Fluid Engineering, 2002，124(2):377-383.

15 KUNZ R，BOGER D，STINEBRING D，et al. A preconditioned implicit method for two-phase flow s with application to cavitation prediction[J]. Computers & Fluids, 2000，29(8):849-875.

16 TAN Lei，ZHU Baoshan，CAO Shuliang，et al. Numerical simulation of unsteady cavitation flow in a centrifugal pump at off-design conditions[J]. Proc. IMech E，Part C: Journal of Mechanical Engineering Science，2014, 228(11): 1994-2006.

17 COUTIER-DELGOSHA O，FORTES-PATELLA R，REBOUD J. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation[J]. ASME Journal of Fluids Engineering, 2003，125(1): 38-45.

18 張淼，薛瑞，皮漫，等. 修正的SSTk-ω模型在云狀空化流動計算中的應用研究[J]. 西北水電，2014(4):76-81. ZHANG Miao，XUE Rui，PI Man，et al. Study on application of the modified SSTk-ωmodel in computation of cloud cavitating flows[J]. Northwest Hydropower，2014(4)：76-81.(in Chinese)

19 KUBOTA A，KATO H. Unsteady structure measurement of cloud cavitation on a foil section[J]. ASME Journal of Fluids Engineering，1989，111(3): 204-210.

20 張德勝，吳蘇青，施衛東，等. 不同湍流模型在軸流泵葉頂泄漏渦模擬中的應用與驗證[J]. 農業工程學報，2013，29(13)：46-53. ZHANG Desheng， WU Suqing， SHI Weidong， et al. Application and experiment of different turbulence models for simulating of the tip leakage vortex in axial flow pump[J]. Transactions of the CSAE，2013，29(13)：46-53.(in Chinese)

21 李曉俊，袁壽其，潘中永，等. 離心泵邊界層網格的實現及應用評價[J]. 農業工程學報，2012，28(20)：67-72. LI Xiaojun，YUAN Shouqi，PAN Zhongyong，et al. Realization and application of near-wall mesh in centrifugal pumps[J]. Transactions of the CSAE，2012， 28(20)：67-72.(in Chinese)

22 趙偉國. 水翼云空化及其抑制機理研究[D]. 杭州：浙江大學，2012.

23 MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]．AIAA Journal，1994, 32(8): 1598-1605.

24 REBOUD J L，STUTZ B，COUTIER O．Two phase flow structure of cavitation experiment and modeling of unsteady effects[C]∥Proceedings of the 3rd International Symposium on Caviation，1998．

25 ZWART P J，GERBER A G，BELAMRI T. A two-phase flow model for predicting cavitation dynamics[C]∥Proceedings of International Conference on Multiphase Flow，2004.

26 JI Bin，LUO Xianwu，WU Yulin，et al. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil[J]. International Journal of Multiphase Flow，2013，51:33-43.

EffectofSurface-fittedObstacleinCentrifugalPumponCavitationSuppression

ZHAO Weiguo1,2ZHAO Guoshou1XIAN Lixia1HAN Xiangdong1

(1.CollegeofEnergyandPowerEngineering，LanzhouUniversityofTechnology，Lanzhou730050，China2.KeyLaboratoryofFluidMachineryandSystem，GansuProvince,LanzhouUniversityofTechnology,Lanzhou730050，China)

Centrifugal pumps are widely used to deliver liquid media in agriculture, pharmacy, industry, petrochemical industry, etc. Compared with the case delivering pure liquid such as water, centrifugal pumps not only have lower efficiency but also are subject to severe vibration, noise and erosion when delivering cavity two-phase flow, leading to the deterioration of flow field and even the shortage of service life. The cavitation flow in centrifugal pump performs strong instabilities, thus a method of a tiny obstacle fitted on the blade surface was proposed to suppress the cavitation development on ans=32 model pump. The unsteady cavitation flow varied with cavitation number in centrifugal pump was simulated by modified SSTk-ωturbulence model combined with Kubota cavitation model. The results showed that the head of centrifugal pump with obstacle was decreased within 5% at various flow rate and within 3% at design point, the efficiency was decreased within 3% at various flow rate and 1.2% at design point, the head with obstacle was great improved when cavitation flow developed. The obstacle can enhance the turbulent kinetic energy near the blade wall and reset the absolute pressure distribution, which can suppress the cavitation at different stages in centrifugal pump. The obstacle can optimize the flow structure and degrade the vortex intensity near the suction side of blade especially the area close to the tongue. The obstacle can decrease the cavity volume at varied cavitation number and the cavity volume keep attenuating when cavitation developed. The obstacle can cause small magnitude of the disturbance on the pressure frequency spectrum. The effects of cavitation suppression were optimal when the bubbles reached close to the obstacle.

centrifugal pump； obstacle； cavitation suppression； numerical simulation

TH311

A

1000-1298(2017)09-0111-10

10.6041/j.issn.1000-1298.2017.09.014

2017-01-05

2017-02-15

國家自然科學基金項目(51269011)

趙偉國(1979—)，男，副教授，主要從事水力機械流動理論及空化多相流研究，E-mail: zhaowg@zju.edu.cn