三自由度氣動柔性驅動器結構功能與形變特性研究

趙云偉 耿德旭 劉曉敏 劉洪波 鄭永永

(1.北華大學工程訓練中心， 吉林 132021； 2.北華大學機械工程學院， 吉林 132021)

三自由度氣動柔性驅動器結構功能與形變特性研究

趙云偉1耿德旭1劉曉敏1劉洪波1鄭永永2

(1.北華大學工程訓練中心， 吉林 132021； 2.北華大學機械工程學院， 吉林 132021)

設計了一種采用伸長型氣動人工肌肉的三自由度柔性驅動器，該驅動器的驅動裝置與本體復合一體，主要由3根對稱分布的人工肌肉并聯組成。根據力和力矩分析，考慮了驅動器伸長量、彎曲方向和彎曲角度的綜合影響，建立了驅動器伸長量、彎曲方向和彎曲角度的非線性理論模型。通過試驗對理論模型進行了驗證，獲得了柔性驅動器在不同通氣方式下的形變性能。結果表明：該柔性驅動器彎曲時近似圓弧狀，具有較高靈活性，能夠實現軸向伸長和空間內任意方向彎曲，可作為執行部件應用于農業機器人和果蔬采摘機械手等仿生機械上。

人工肌肉； 氣動柔性驅動器； 空間彎曲； 形變特性

引言

隨著現代農業的迅速發展和勞動力生產成本的日益增加，智能農業機器人被廣泛應用以提高生產率，降低人工蔬果采摘成本[1-3]。農作物果蔬形狀和尺寸各異，需求適應性好的采摘機械手。柔性關節構成的機械手具有較好的靈活性，適于作為農業機器人的果蔬采摘執行器。近年來國內外學者在柔性驅動器的驅動材料、結構優化和柔性控制實現等方面進行了大量研究。柔性驅動器根據驅動方式可以分為電動機驅動、功能材料驅動和流體驅動等[4-7]。氣體驅動是流體驅動器的一種常見方式，具有部件少、質量低、成本低、工作溫度低和柔順性高等特點[8]。典型的氣動柔性驅動器為McKibben型人工肌肉[9-10]，主要利用橡膠氣囊徑向膨脹產生拉力進行工作。許多學者都對其控制方式進行了研究，并將人工肌肉組成關節在機械手上進行應用[11-12]。文獻[13-14]應用氣動人工肌肉研制了并聯結構三自由度驅動器，并對該驅動器的動力學模型和非線性控制進行了研究。浙江工業大學機電研究所采用3個氣動柔性驅動器研制了一種新型氣動柔性球關節[15]，通過向3個柔性驅動器內輸入不同的氣壓實現其旋轉運動。20世紀80年代日本Toshiba公司采用內部附有尼龍螺旋纖維線的橡膠管研制了一種氣動柔性微型驅動器[16]，該驅動器具有多個自由度，內部為3個對等分布的氣室。SUZUMORI等[17-18]分析了該驅動器靜力學特性和動力學特性，并研制了未嵌入尼龍纖維的柔性驅動器，將其應用于多指機械手。于蓮芝等[19]采用三自由度空氣壓橡膠驅動器研制成具有柔性移動機構的微小機器人內窺鏡診療系統。

傳統柔性驅動器通常是關節本體和驅動裝置相對獨立，運動和驅動柔性多數依賴于控制技術，體積、剛度和慣性較大，靈活性和適應性差，目前已有的氣動驅動器尚不能完全滿足仿生及特種機器人等領域的特殊需要。為了解決現階段柔性驅動器存在的問題，本文采用自主研發的軸向膨脹型人工肌肉設計一種三肌肉氣動復合彈性體結構的柔性驅動器。

1 柔性驅動器結構與功能

設計的氣動柔性驅動器由3個對稱均布互成120°的氣動人工肌肉和彈性骨架并聯組成。人工肌肉為氣囊與端蓋之間形成的封閉腔體，外部為套裝的薄片狀約束環，肌肉之間添加彈性骨架，如圖1所示。彈性骨架起到支撐和連接作用，可提高柔性驅動器剛度和彈性恢復，保證驅動器運動功能的實現。

圖1 氣動柔性驅動器Fig.1 Flexible pneumatic actuator1.氣囊 2.約束環 3.上端蓋 4.彈性骨架 5.下端蓋 6.氣動接頭

驅動器制作工藝較為復雜，氣囊通常采用乳膠管和硅膠管，彈性骨架采用彈簧等彈性元件，約束環和端蓋采用ABS塑料3D打印而成。在制作時，首先將通氣軟管與下接頭進行壓裝，然后聯同上接頭采用鋼絲扎緊方式封裝氣囊，為保證氣密性，預先套裝約束環進行通氣試驗；然后依次將氣囊與彈性骨架(圓柱螺旋彈簧)與下端蓋連接，端蓋設有匹配的安裝凹槽；彈簧兩端設有堵頭，堵頭端部設有螺紋孔可與端蓋用螺釘配合連接；氣囊下接頭側面設有螺紋孔與下端蓋通過螺釘配合連接；然后依序套裝約束環，最后將氣囊和彈簧與上端蓋采用螺釘連接方式裝配，完成驅動器制作。

通入壓縮氣體后，驅動器內人工肌肉的氣囊內壁受壓發生膨脹，外部由于約束元件的徑向束縛產生軸向力驅動關節運動。驅動器的功能特性如圖2所示。未通氣時，驅動器狀態如圖2a所示；當3根肌肉同時通入相同氣壓時，柔性驅動器沿軸線方向伸長，如圖2b所示；當單根或2根肌肉組合通氣時，驅動器伸長的同時發生彎曲，如圖2c和圖2d所示；當3根肌肉通入不同氣壓時，驅動器向空間不同方向彎曲，如圖3所示。

圖2 驅動器功能特性Fig.2 Functional characteristics of FPA

驅動器彎曲時沿約束環邊緣處做類似圓弧狀彎曲，具有無軸多鉸鏈的彈性彎曲特征，如圖4a所示。單根肌肉和2根肌肉分別通氣下驅動器內側彎曲輪廓的數據點進行圓弧擬合，如圖4b所示。

圖3 驅動器彎曲方向Fig.3 Bending direction of FPA

圖4 驅動器彎曲弧線Fig.4 Bendingarc of FPA

由驅動器內側彎曲曲線上數據點到圓心的距離與擬合圓半徑進行對比，可得到驅動器彎曲圓弧誤差。單根肌肉驅動時驅動器彎曲圓弧誤差為0.29%，2根肌肉驅動時驅動器彎曲圓弧誤差為0.49%。對比結果表明，驅動器彎曲時沿約束環一側做圓弧狀彎曲。

2 柔性驅動器軸向受力和形變分析

通入壓縮氣體后，驅動器端部同時受軸向力和彎曲力矩的共同作用，產生復合變形。軸向力決定驅動器的伸長量，端蓋處的合力矩決定驅動器彎曲的角度和方向。

圖5為驅動器的軸向伸長變形。R1、R2、R3和T1、T2、T3分別為組成關節的3個人工肌肉和3個彈性骨架。人工肌肉通入氣壓pi=p，其中i=1,2,3，為肌肉編號。

圖5 驅動器軸向變形與受力分析Fig.5 Axial deformation and stress analysis of FPA

通入壓縮氣體后，人工肌肉內壁受壓膨脹，壓縮氣體在驅動器端蓋部產生驅動力Fpi。驅動器在軸向力作用下，沿軸向方向自由伸長變形。驅動器軸向變形過程中，彈性骨架和人工肌肉產生相應的軸向應變，阻礙驅動器伸長產生阻抗力。

根據驅動器軸向靜力平衡方程可知

(1)

式中FTi——彈性骨架阻抗力FRi——人工肌肉阻抗力

2.1 軸向驅動力

壓力氣體在驅動器端蓋產生驅動力為

Fpi=piSi

(2)

式中Si——肌肉變形后內腔橫截面面積

圖6 肌肉變形前后幾何關系Fig.6 Geometric relationship between undeformed and deformed muscles

人工肌肉軸向變形過程中，因肌肉內壁受壓拉伸變薄，肌肉內腔工作截面發生變化,如圖6所示。

構成肌肉的橡膠材料是各向同性不可壓縮的超彈性體，由變形前后膠囊體積不變可得肌肉變形后內腔橫截面積。肌肉變形后體積V為

V=ΔS0l0=ΔS′(l0+Δl)

(3)

式中 ΔS0——變形前肌肉環形截面積 ΔS′——變形后肌肉環形截面積l0——人工肌肉有效原始長度 Δl——人工肌肉伸長量

由于人工肌肉伸長后約束環間存在間隙，不能完全限制膠管外側形變(圖7，d表示約束環厚度，δ表示約束環間初始間隙)，膠管外側將沿約束環的間隙膨脹，肌肉初始橫截面積S0將增加，因此需要加入肌肉內腔橫截面積修正量ΔS。肌肉變形前后的環形截面積為

(4)

式中S——肌肉變形前內腔橫截面積D1——乳膠管原始外徑D2——乳膠管原始內徑將式(4)代入式(3)可得，肌肉變形后的內腔橫截面面積為

圖7 0.3 MPa下不同約束邊界下乳膠管變形Fig.7 Deformation of rubber tube under different constraint boundary conditions when air pressure was 0.3 MPa

(5)

式中，ΔS與約束環形狀、尺寸和排列間隙有關，可由理論值與實驗數據對比求得。

2.2 彈性骨架阻抗力

彈性骨架阻礙驅動器軸向伸長時產生阻抗力，根據Hooke定律，彈性骨架阻抗力為

FTi=kTΔl

(6)

其中

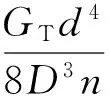
(7)

式中kT——彈簧剛度GT——彈簧剪切彈性模量D——彈簧中徑n——彈簧圈數d——鋼絲直徑

2.3 人工肌肉阻抗力

驅動器軸向伸長時，人工肌肉同樣產生相同的軸向應變，阻礙其伸長。假設約束環完全限制人工肌肉外側變形，且肌肉伸長時不發生扭轉，由Neo-Hookean模型推導出人工肌肉軸向伸長時阻抗力[20]為

(8)

式中GR——肌肉剪切彈性模量

當3根人工肌肉通入相同氣壓時，驅動器端蓋處的合力矩為零，驅動器僅受到軸向力作用，只產生軸向變形。假設彈性骨架和人工肌肉軸向變形量協調同步，忽略二者耦合力影響，且變形力符合線性疊加。將式(2)、式(6)和式(8)代入式(1)，忽略高次微小量，驅動器軸向伸長量為

(9)

3 驅動器彎曲變形分析

當3根人工肌肉通入不同氣壓時，除軸向變形外，驅動器受到端部力矩作用向空間不同方向彎曲變形(圖8a)。此時，驅動器端部合力矩Mg方向即為彎曲方向；彈性骨架和人工肌肉隨驅動器彎曲變形產生相同的彎曲形變，阻礙驅動器彎曲產生阻抗力力矩，如圖8b、8c所示。

圖8 柔性驅動器彎曲變形Fig.8 Bending properties of FPA

通入壓縮氣體后，驅動器端部受到的力矩為

(10)

單個人工肌肉產生的力矩為

Mi=piSil(i=1,2,3)

(11)

式中l——人工肌肉中心到關節中心的距離

3.1 驅動器彎曲方向

根據驅動器端蓋處受到力矩分析(圖9)可知，驅動器彎曲方向角為

(12)

其中Mgx=(M2+M3)sinα-M1

(13)

Mgy=(M3-M2)cosα

(14)

式中Mgx——合力矩在X方向分量Mgy——合力矩在Y方向分量α——人工肌肉驅動力矩方向與Y軸的夾角由圖9幾何關系求得α=π/6。

圖9 柔性驅動器彎曲方向Fig.9 Analysis on bending direction of FPA

將式(13)和式(14)代入式(12)得合力矩彎曲方向與通入氣壓的關系為

(15)

3.2 驅動器彎曲角度

當3根人工肌肉通入不同氣壓時，驅動器開始向不同方向彎曲。此時，驅動器除受到軸向力，還將受到壓力氣體在端部產生彎曲力矩M。驅動器外部的約束環只作為約束鉸鏈，限制內部乳膠管的徑向膨脹，不產生阻抗力矩。因此阻礙柔性驅動器彎曲變形的因素有2項，分別為彈性骨架產生的阻抗力矩MT和人工肌肉產生的阻抗力矩MR。

根據驅動器彎曲力矩平衡方程可知

(16)

驅動器在壓縮氣體的作用下沿中性層彎曲，肌肉和彈性骨架與中性層距離如圖10所示。柔性驅動器內人工肌肉與彈性骨架分布在同一圓周上。

圖10 肌肉和彈性骨架與中性層距離Fig.10 Distance from muscle and elastic skeleton to neutral layer

由于人工肌肉中心對稱分布，驅動器在等分的3個區域Ⅰ、Ⅱ和Ⅲ內彎曲情況相同。

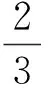
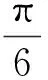
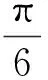
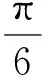
(1)驅動力矩

此時，肌肉R2、R3伸長，R1壓縮。驅動器端部驅動力矩為人工肌肉驅動力矩在中性層平面法向分量

(17)

其中由圖10幾何關系可知

(18)

式中l1、l2、l3——人工肌肉中心到驅動器彎曲變形中性層距離

(2)彈性骨架阻抗力矩

彈性骨架T2伸長，T1、T3壓縮。由于驅動器彎曲時為圓弧狀，則驅動器彎曲狀態下的變形協調方程為

(19)

彈性骨架阻礙驅動器彎曲變形時，除繞本體彎曲時產生的彎曲力矩Mk外，還有繞驅動器彎曲中心彎曲的耦合力矩M′Ti(圖8b)。

根據變形協調條件，假設彈性骨架彎曲力矩符合線性疊加，并考慮彈性骨架軸向產生的耦合力矩，可知彈性骨架負載力矩為

(20)

式中l′1、l′2、l′3——彈性骨架中心到驅動器彎曲變 形中性層的距離，由圖10幾何關系可知l′1=l3，l′2=l1，l′3=l2

Mk——彈簧彎曲力矩

根據圓柱螺旋彈簧受純彎矩變形公式，考慮預應力對圓柱螺旋彈簧彎曲變形的影響[21]，可得圓柱螺旋彈簧的彎曲力矩為

(21)

式中E1——彈簧彈性模量μ——泊松比

(3)人工肌肉阻抗力矩

人工肌肉彎曲時產生的阻抗力矩與彈性骨架相同，包含本體阻抗力矩Mn和耦合力矩M′Ri(圖8c)。

驅動器彎曲狀態下肌肉的變形協調方程為

(22)

同理，可知肌肉負載力矩為

(23)

其中

(24)

式中Mn——肌肉彎曲力矩kR——乳膠管軸向剛度

乳膠管本體的彎曲力矩與轉角的關系[22]為

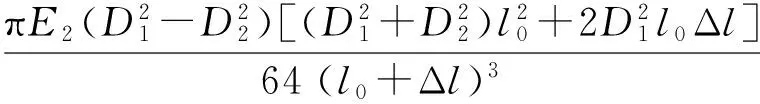
(25)

式中E2——乳膠管彈性模量

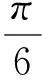
肌肉R3伸長，R1、R2壓縮；彈性骨架T2、T3伸長，T1壓縮。

驅動器驅動力矩為

(26)

其中

(27)

驅動器彎曲狀態下彈性骨架和肌肉的變形協調方程分別為

(28)

(29)

彈性骨架和肌肉的阻抗力矩分別為

(30)

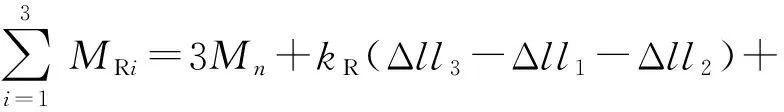
(31)

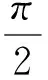
肌肉R1、R2伸長，R3壓縮；彈性骨架T3伸長，T1、T2壓縮。

驅動器驅動力矩為

(32)

其中

(33)

驅動器彎曲狀態下彈性骨架和肌肉的變形協調方程分別為

(34)

(35)

彈性骨架和肌肉的阻抗力矩分別為

(36)

(37)

將式(11)～(37)代入式(10)可得，驅動器在第Ⅰ區域內的彎曲角度。

4 試驗與分析

柔性驅動器的彎曲試驗裝置如圖11所示。該試驗裝置主要由氣源、精密減壓閥、單片機、陀螺儀和磁羅盤傳感器組成。通過減壓閥調節3個人工肌肉通入的氣體壓力，控制驅動器的彎曲方向和彎曲角度，采用陀螺儀和磁羅盤傳感器測量驅動器的彎曲方向角和彎曲角度，再經由Freescale單片機進行數據采集和計算。驅動器有效長度為50 mm，直徑30 mm，質量200 g。約束環材料為ABS塑料，驅動器具體材料參數如表1所示。

圖11 驅動器靜力學試驗裝置Fig.11 Static experimental devices of FPA1.單片機 2.精密減壓閥 3.柔性驅動器 4.陀螺儀和磁羅盤傳感器

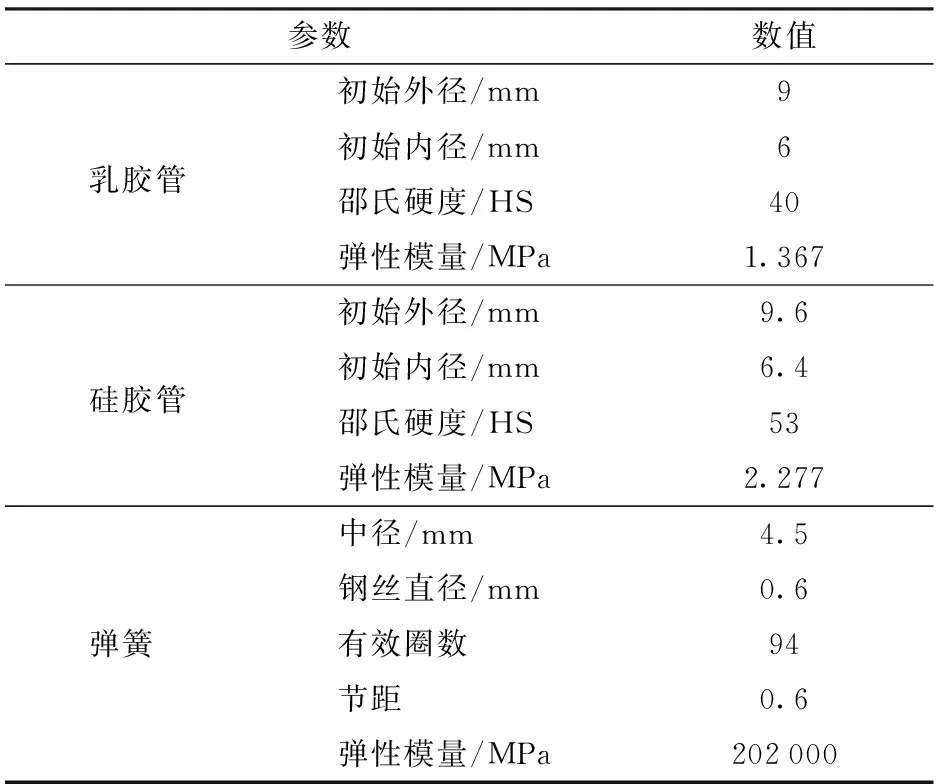
參數數值初始外徑/mm9乳膠管初始內徑/mm6邵氏硬度/HS40彈性模量/MPa1.367初始外徑/mm9.6硅膠管初始內徑/mm6.4邵氏硬度/HS53彈性模量/MPa2.277中徑/mm4.5鋼絲直徑/mm0.6彈簧有效圈數94節距0.6彈性模量/MPa202000

4.1 肌肉變形前內腔橫截面積

人工肌肉內腔橫截面積與氣壓的關系如圖12所示。將采用厚度為2 mm，間隙分別為0 mm和1 mm圓柱狀約束環的人工肌肉內腔橫截面積的理論計算結果與試驗測得的數據進行擬合，可得內腔面積修正量ΔS分別為15.5 mm2和17.5 mm2。由圖12可以看出，理論計算值和試驗數據趨勢一致，吻合較好。隨著氣壓的增加，人工肌肉內腔橫截面積隨之增大。通過調整通入氣體壓力，可以控制人工肌肉的形變量。

圖12 肌肉內腔橫截面積隨氣壓的變化曲線Fig.12 Variation curves of cross-sectional area of muscle with air pressure

4.2 驅動器軸向伸長

圖13為采用不同氣囊材料的柔性驅動器在不同氣壓下的伸長量。

圖13 驅動器伸長量隨氣壓的變化曲線Fig.13 Variation curves of elongation of FPA with air pressure

從圖13可以看到，驅動器的伸長量理論計算與試驗數據趨勢一致，吻合較好，其伸長量隨著通入氣壓的增加而增加。由于在不同壓強下肌肉變形后內孔橫截面不同，肌肉驅動力不一致。導致驅動器的伸長量呈非線性變化。由于硅膠管的硬度和彈性模量較強，其伸長量小于乳膠管。

4.3 驅動器彎曲方向

驅動器彎曲的起始方向為X軸正向(圖9)。將表1所示驅動器參數和通入的氣壓代入式(15)可得如圖14所示的驅動器彎曲方向隨氣壓變化情況。驅動器彎曲方向理論計算與試驗數據對比可知，驅動器彎曲方向的理論計算與試驗數據趨勢一致，吻合較好，能夠真實地反映通氣后驅動器的彎曲方向。在p1和p2通入氣壓保持恒定不變時，隨著人工肌肉通入氣壓p3的增加，驅動器的彎曲方向角隨之增加或減小。

圖14 驅動器彎曲方向角隨氣壓的變化曲線Fig.14 Variation curves of bending direction of FPA

保持其中1根通入氣壓恒定不變，通過調整其它2根人工肌肉通入的氣壓，可以控制驅動器在0～360°范圍內任意方向彎曲，如圖15所示。當p1、p2、p3分別通入0.35 MPa氣壓時，驅動器彎曲方向可由其他2根肌肉通入的氣壓進行控制。驅動器彎曲方向角120°和240°為人工肌肉通氣變更的分界線，隨著氣壓的增加驅動器彎方向角變化趨勢平緩。

圖15 驅動器彎曲方向角隨氣壓的變化曲面Fig.15 Variaton surfaces of bending direction of FPA with air pressure

4.4 驅動器彎曲角度

圖16為驅動器彎曲角度隨氣壓的變化。由圖16可知，理論計算值和試驗數據趨勢一致，曲線吻合較好。當p1和p2通入相同氣壓，p3不通氣時或p1和p2不通氣，p3通氣時，驅動器彎曲角度隨通入氣壓的增加而增大。

通過調整3根人工肌肉通氣壓力，可實現驅動器向不同方向彎曲，其彎曲角度如圖17所示。由圖中可知，p1通入氣壓保持不變時，隨著p2和p3通入氣壓的增加，驅動器彎曲角度逐漸增加并呈非線性變化，彎曲角度范圍為0°～57.8°。驅動器彎曲角度最大值為雙肌肉驅動時，即p1=0，p2=p3=0.35 MPa(圖17a)。驅動器彎曲角度最小值為3根肌肉通入相同氣壓時，即p1=p2=p3，驅動器僅伸長不彎曲，此時彎曲角度為0°。

圖16 驅動器彎曲角度隨氣壓的變化曲線Fig.16 Variation curves of bending angle of FPA

圖17 驅動器彎曲角度隨氣壓的變化曲面Fig.17 Variation surfaces of bending angle with air pressure

5 驅動器在農業采摘領域應用

三自由度柔性驅動器具有較好的柔性，可以實現軸向伸長和向空間任意方向彎曲，可作為機械手的末端執行器。采用該驅動器研制的三指氣動柔性果蔬采摘機械手，其結構如圖18所示。該機械手包含3個柔性手指和1個柔性腕部，具有10個自由度，可實現抓、握、夾和擰等功能，適于抓取蘋果、桔子和西紅柿等球形果蔬。

圖18 柔性機械手結構圖Fig.18 Structure diagram of flexible robot hand1.手腕 2.手掌 3.手指 4.三自由度柔性驅動器

6 結束語

氣動柔性驅動器由3根伸長型人工肌肉并聯組成。通入壓縮氣體后，驅動器為彈性體變形，能實現彎曲和伸長。外部約束環作為約束鉸鏈，沿約束環一側做圓弧狀彎曲，其彎曲方向和角度主要取決于驅動器端蓋受到的合力矩的大小和方向。建立了驅動器在氣壓下的形變理論模型，獲得了其軸向伸長量、彎曲方向和彎曲角度與通入氣壓的變化規律。試驗結果表明，通過控制人工肌肉內氣體壓力，該柔性驅動器可以實現軸向伸長，向空間任意方向和不同角度彎曲。驅動器伸長量和彎曲角度隨著通入氣體壓強增加而增大，且驅動器彎曲方向角過渡平滑，適于作為末端執行器應用在果蔬采摘機械手上。在0.35 MPa下，形變后其軸向伸長量可達50%，彎曲角度可達60°，彎曲方向角范圍為0°～360°。

1 王燕,楊慶華,鮑官軍,等. 關節型果蔬采摘機械臂優化設計與試驗[J]. 農業機械學報, 2011, 42(7): 191-195. WANG Yan, YANG Qinghua, BAO Guanjun, et al. Optimization design and experiment of fruit and vegetable picking manipulator[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(7):191-195.(in Chinese)

2 李國利, 姬長英, 顧寶興,等. 多末端蘋果采摘機器人機械手運動學分析與試驗[J/OL]. 農業機械學報, 2016, 47(12):14-21.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20161203&journal_id=jcsam. DOI：10.6041 /j issn.1000-1298.2016.12.003. LI Guoli, JI Changying, GU Baoxing, et al. Kinematics analysis and experiment of apple harvesting robot manipulator with multiple end-effectors[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(12):14-21.(in Chinese)

3 傅隆生, 張發年, 槐島芳德,等. 獼猴桃采摘機器人末端執行器設計與試驗[J/OL].農業機械學報, 2015, 46(3):1-7. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150301&journal_id=jcsam. DOI：10.6041 /j.issn.1000-1298.2015.03.001. FU Longsheng, ZHANG Fanian, GEJIMA Y, et al. Development and experiment of end-effector for kiwifruit harvesting robot[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3):1-7.(in Chinese)

4 KORAYEM M H, RAHIMI H N, NIKOOBIN A. Mathematical modeling and trajectory planning of mobile manipulators with flexible links and joints [J]. Applied Mathematical Modelling, 2012,36(7): 3229-3244.

5 HARAGUCHI D，TADANO K, KAWASHIMA K. Development of a pneumatically-driven robotic forceps with a flexible wris joint [J]. Procedia CIRP, 2013, 5: 61-65.

6 KORAYEM M H, RAHIMI H N, NIKOOBIN A. Flexible artificial muscle actuator using coiled shape memory alloy wires [J]. APCBEE Procedia, 2013, 7:54-59.

7 ZHANG J J, YIN Y H. SMA-based bionic integration design of self-sensor-actuator-structure for artificial skeletal muscle [J]. Sensors and Actuators A:Physical, 2012, 181:94-102.

8 CHEN D H, USHIJIM K. Prediction of the mechanical performance of McKibben artificial muscle actuator[J]. International Journal of Mechanical Sciences, 2014, 78:183-192.

9 GREEF A D, LAMBERT P, DELCHAMBRE A. Towards flexible medical instruments: review of flexible fluidic actuators [J]. Precision Engineering, 2009, 33:311-321.

10 TAKASHIMA K, ROSSITER J, MUKAI T. McKibben artificial muscle using shape-memory polymer [J]. Sensors and Actuators A:Physical, 2010, 164:116-124.

11 WICKRAMATUNGE K C, LEEPHAKPREEDA T. Empirical modeling of dynamic behaviors of pneumatic artificial muscle actuators [J]. ISA Transactions, 2013, 52:825-834.

12 NUCHKRUA T, LEEPHAKPREEDA T. Fuzzy self-tuning PID control of hydrogen-driven pneumatic artificial muscle actuator[J]. Journal of Bionic Engineering, 2013, 10(3):329-340.

13 SHI G L, SHEN W. Hybrid control of a parallel platform based on pneumatic artificial muscles combining sliding mode controller and adaptive fuzzy CMAC[J]. Control Engineering Practice, 2013, 21(1): 76-86.

14 ZHU X C, TAO G L, YAO B, et al. Adaptive robust posture control of a parallel manipulator driven by pneumatic muscles [J]. Automatica, 2008, 44(9):2248-2257.

15 李尚會, 楊慶華, 鮑官軍, 等. 基于FPA 的新型氣動柔性球關節的研究[J]. 浙江工業大學學報, 2009, 37(6): 662-666. LI Shanghui, YANG Qinghua , BAO Guanjun , et al. Research on flexible pneumatic spherical joint based on FPA[J]. Journal of Zhejiang University of Technology, 2009, 37(6): 662-666. (in Chinese)

16 SUZUMORI K, IIKURA S, TANAKA H. Flexible microactuator for miniature robots[C]∥Proceedings of the 1991 IEEE Workshop on Micro Electro Mechanical Systems, 1991: 204-209.

17 SUZUMORI K, IIKURA S, TANAKA H. Applying a flexible microactuator to robotic mechanisms [J]. IEEE Control Systems, 1992, 12(1): 21-27.

18 SUZUMORI K, MAEDA T, WATANABE H, et al. Fiberless flexible microactuator designed by finite-element method [J]. IEEE/ASME Transactions on Mechatronics, 1997, 2(4): 281-286.

19 于蓮芝,顏國正,馬官營,等. 一種柔性移動微小機器人系統的驅動力學特性分析[J]. 儀器儀表學報, 2007, 28(1): 7-11. YU Lianzhi, YAN Guozheng, MA Guanying, et al. Analysis of actuating mechanics characteristics for a flexible miniature robot system[J]. Chinese Journal of Scientific Instrument, 2007, 28(1): 7-11. (in Chinese)

20 GENG D X, ZHAO J, ZHANG L, et al. Mechanical Properties analysis on elongation type of pneumatic artificial muscles[C]∥2nd International Conference on Mechanical, Industrial, and Manufacturing Technologies, 2011: 437-441.

21 鐘文彬, 李柏林, 晏星凡. 預應力圓柱螺旋彈簧彎曲彈性特性研究[J]. 機械設計, 2008, 25(1):25-27. ZHONG Wenbin, LI Bailin, YAN Xingfan. Characteristic research on bending elasticity of prestressed cylindrical helical spring[J].Journal of Machine Design, 2008, 25(1):25-27. (in Chinese)

22 GENG D X, ZHAO J, ZHANG L. Study on bidirectional controllable flexible bending joints based on elongation artificial muscles [J]. Applied Mechanics and Materials, 2011, 44-47: 2883-2887.

StructureandDeformationCharacteristicsof3-DOFPneumaticFlexibleActuator

ZHAO Yunwei1GENG Dexu1LIU Xiaomin1LIU Hongbo1ZHENG Yongyong2

(1.EngineeringTrainingCenter,BeihuaUniversity,Jilin132021,China2.CollegeofMechanicalEngineering,BeihuaUniversity,Jilin132021,China)

A type of 3-DOF flexible pneumatic actuator (FPA) employing elongation pneumatic artificial muscles was developed. It was mainly composed by three pneumatic artificial muscles symmetrically distributed in parallel and three artificial muscles were fixed 120° each other in space. The pneumatic artificial muscle was a closed cavity formed by the rubber tube and the end covers, and the outer side of it was thin sheet restraint rings set compacted. The elastic skeletons were added among the artificial muscles to improve the rigidity and stability of FPA. Specially, the driving device of FPA was just the body of the actuator. The FPA has the advantages of small volume, light weight and multiple degrees of freedom, and it can axially elongate and bend in any direction by controlling the input gas pressure of different artificial muscles. According to the force and torque analysis, the nonlinear theoretical model was developed to simultaneously describe the elongation, bending direction and bending angle of the FPA. Further, the theoretical model was verified by experiments, and then the deforming properties of FPA were obtained under different ventilation modes. The results showed that the FPA was in arc shape approximately when it was bent; it had high flexibility to elongate in axial direction or bend in any direction which had the similarity to the biological muscles in the body flexibility, movement and driving ability. In summary, this type of FPA can be as flexible fingers or flexible joints applied to fruit and vegetable picking manipulator or agricultural robot.

artificial muscle; pneumatic flexible actuator; spacing bending; deformation characteristics

TH138.5

A

1000-1298(2017)09-0392-10

10.6041/j.issn.1000-1298.2017.09.050

2016-12-29

2017-03-07

國家自然科學基金項目(51275004)、吉林省自然科學基金項目(20150101026JC)、吉林省科技發展計劃項目(20150520109JH)、吉林省教育廳“十二五”科學技術研究項目(20150158)和北華大學青年教師提升計劃項目

趙云偉(1978—)，男，副教授，博士，主要從事智能精密制造和機器人技術研究，E-mail： jluzyw@163.com

耿德旭(1964—)，男，教授，博士，主要從事智能精密制造、機械系統動力學和機器人技術研究，E-mail： gengdx64@163.com