非線性四階薛定諤方程的高階保能量方法

王一帆， 孫建強， 陳宵瑋

(海南大學 信息科學技術學院， 海南 海口 570228)

非線性四階薛定諤方程的高階保能量方法

王一帆， 孫建強， 陳宵瑋

(海南大學 信息科學技術學院， 海南 海口 570228)

利用四階平均向量場方法和擬譜方法構造非線性四階薛定諤方程的高階保能量格式，并用構造的高階保能量格式數值模擬方程孤立波的演化行為.結果表明:新的格式具有很好的穩定性，可以很好地模擬孤立波的演化行為，同時,保持了方程的離散能量守恒特性.

平均向量場方法； 高階保能量方法； 非線性四階薛定諤方程; 譜方法

Abstract： The fourth order energy preserving scheme for the nonlinear fourth-order Schr?dinger equation is obtained by applying the fourth order average vector field method and the Fourier pseudo spectral method. The new fourth order energy preserving scheme is applied to simulate the solitary wave behaviors of the equation. Results show that the new scheme has nice stability and can well simulate the solitary wave evolution behaviors, moreover, it preserves the discrete energy conservation.

Keywords： average vector field method; energy-preserving method; nonlinear fourth-order Schr?dinger equation； spectral method

在已有文獻中，許多學者構造了非線性四階薛定諤方程的不同數值算法.Kong等[1]基于分步數值方法和多辛龍格-庫塔方法的思想，設計了一種新的多辛積分因子，即分步多辛(SSMS)方法.黃浪揚[2]構造了非線性四階薛定諤方程的半顯式多辛擬譜格式.這些格式在長時間精確數值模擬非線性四階薛定諤方程的演化中具有重要的意義，但只能近似地保持方程的能量.近年來，有學者提出在時間方向上具有二階精度的平均向量場方法，能保持微分方程固有能量守恒特性.二階平均向量場方法已經廣泛地應用于計算能量守恒的偏微分方程中[3-5]，并取得了很好的數值結果.如Quispel等[6]提出了具有高階精度的平均向量場方法.本文利用四階平均向量場方法和擬譜方法構造非線性四階薛定諤方程的高階保能量格式，并利用高階保能量格式數值模擬非線性四階薛定諤方程孤立波的演化行為.

1 非線性四階薛定諤方程

考慮強激光光束傳輸過程中四階色散項在具有克爾非線性的松散介質中的影響，文獻[7-9]建立了四階薛定諤方程，即

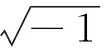
如果考慮外部受限的勢能，則方程(1)為受限制的非線性四階薛定諤方程.文中研究的非線性四階薛定諤方程為

式(2)～(4)中：u0(x)為一個指定的復值函數；g(x)為繞原點的波函數.方程在研究動態玻色-愛因斯坦凝集態、非線性光學之類的問題中具有重要的應用.方程(2)在有限區域內具有能量守恒特性[10]，即

2 非線性四階薛定諤方程的高階保能量格式

下面給出非線性四階薛定諤方程的離散格式.在實際計算中，只能給出方程在有限區域內的數值解.根據文獻[1,10],取方程空間求解區域為[0,2π].

設u(x,t)=p(x,t)+q(x,t)i，方程(2)可表示為

方程(6),(7)可以轉化為無窮維哈密爾頓系統,即

式(8)中:z=(p,q)T,哈密爾頓函數為

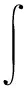
利用擬譜方法在空間方向離散非線性四階薛定諤方程(8),空間積分區間Ω=[0,2π],L=2π，將Ω分為N等分，h=L/N為空間步長，N為一個正偶數.

空間置配點xj=a+hj,j=0,…,N-1.令pj為p(x,t)在配置點xj處的近似值.定義

SN={gj(x);-N/2≤j≤N/2-1}

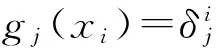
其中:cl=1(|l|≠N/2)；c-N/2=cN/2=2；μ=2π/L.對任意p(x,t)∈C0(Ω)，定義的插值算子IN[11]為

(x).

正交的三角插值算子IN在置配點xj滿足

INp(xj,t)=p(xj,t),j=0,…,N-1.

假設P=(p0,p1,…,pN-1)T，定義

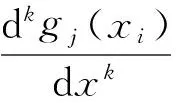
稱Dk為k階微分矩陣.通過計算可以得到

D1,D2分別是一階和二階譜矩陣,即

利用二階微分矩陣D2近似二階偏導算子?xx，可以得到方程(6),(7)的半離散擬譜格式，即

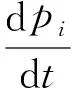
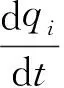
式(10)，(11)中:A=(D2)2；j=0,1,…,N-1.式(10)，(11)可以表示為有限維哈密爾頓系統，即

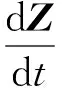
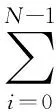
用四階平均向量場方法離散哈密爾頓系統(12)，可得方程(2)的高階保能量格式為

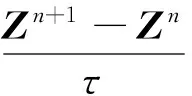
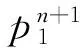
式(13)可以被表示為矩陣向量形式，即

式(15),(16)等價于

式(14)可以表示為

A(τ,h)Un+1=B(τ,h)Un+τF(Un+1,Un),n=1,2,….

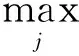
3 數值模擬

為了驗證高階保能量格式(14)的保能量守恒特性，定義相對能量誤差為

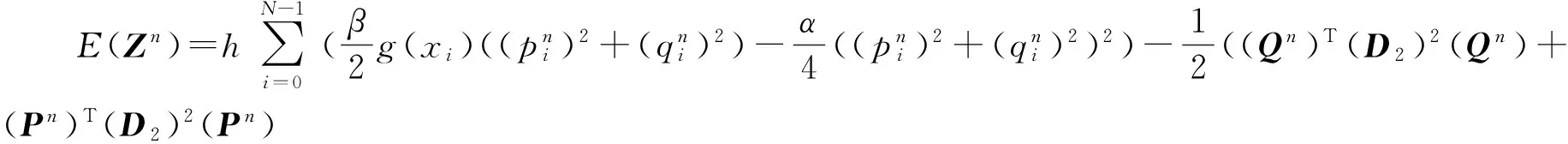
3.1數值模擬1

選擇α=6，β=150，g(x)=sin2x，取方程(2)的初值條件為

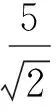
周期L=2π,取時間步長τ=0.000 1，空間置配點N=20.非線性四階薛定諤方程在t=2時刻的實部的數值解Re(μ)和虛部的數值解Im(μ),如圖1所示.方程在t∈[0,2]內的相對能量誤差RE，如圖2所示.圖2中：能量誤差達到機器精度，可忽略.由圖1，2可知：高階保能量格式(14)可以很好地模擬方程孤立波的演化行為，且精確地保持了方程的離散能量守恒特性.

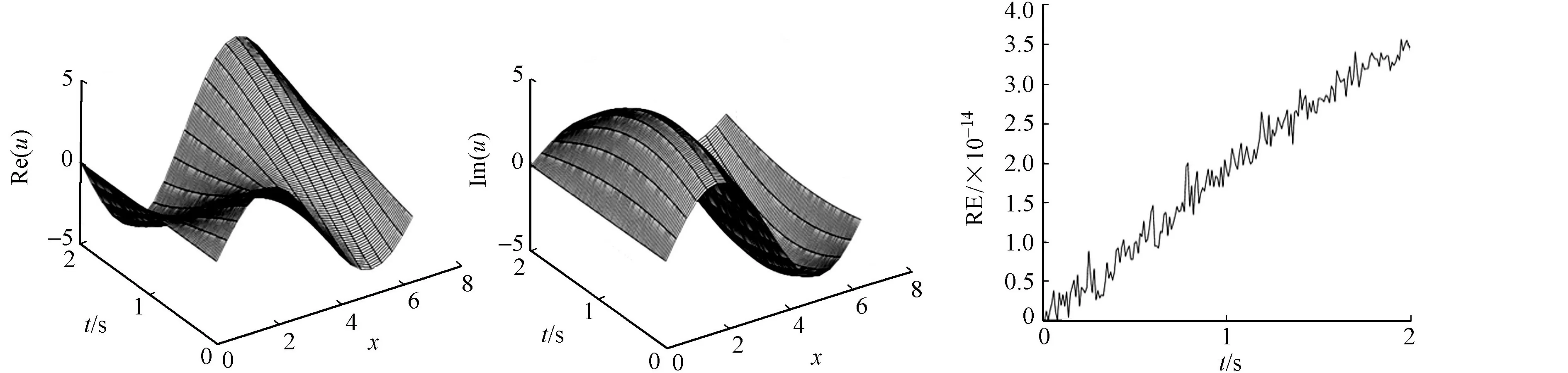
(a) 實部 (b) 虛部 圖1 孤立波在t=2時的實部和虛部的數值解 圖2 孤立波在t∈[0,2]內的相對能量誤差變化Fig.1 Numerical solution of solitary wave at t=2 Fig.2 Relative energy errors of solitary wave at t∈[0,2]

3.2數值模擬2

取α=1,β=1,g(x)=cos2x，取方程(2)初值條件為

u(x,0)=exp(iπ/6)cosx.

L=2π,取時間步長τ=0.000 01，空間置配點N=20.方程在t=1時刻的實部和虛部的數值解,如圖3所示.方程在t∈[0,1]內的相對能量誤差，如圖4所示.圖4中：能量誤差小，同樣可忽略.因此，高階保能量格式有好的計算精度，并且同樣可以精確保持方程的離散能量守恒特性.

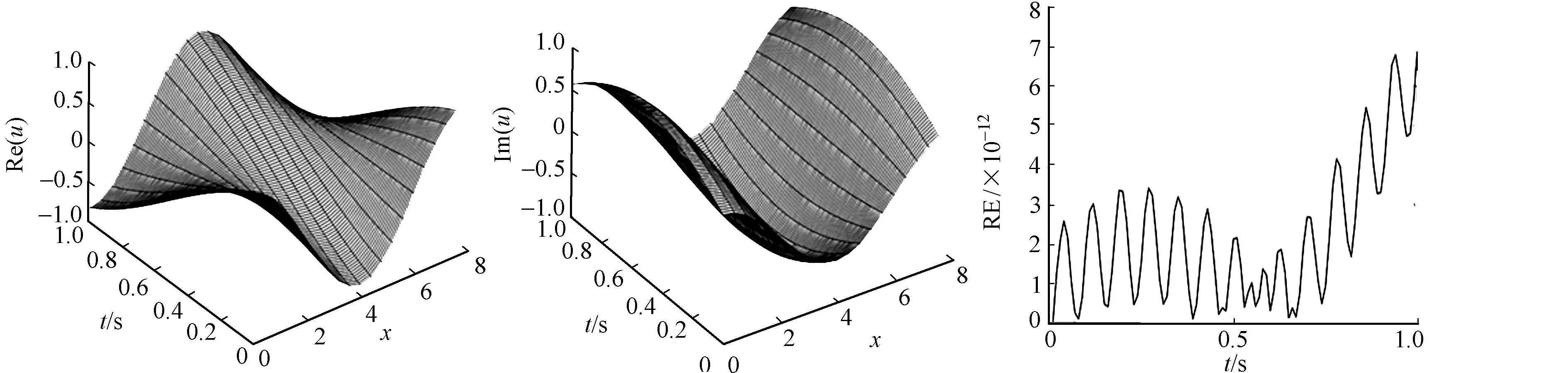
(a) 實部 (b) 虛部圖3 孤立波在t=1時實部和虛部的數值解 圖4 孤立波在t∈[0,1]內的相對能量誤差變化Fig.3 Numerical solution of solitary wave at t=1 Fig.4 Relative energy errors of solitary wave at t∈[0,1]

4 結束語

基于四階平均向量場方法,構造了非線性四階薛定諤方程的高階保能量格式.利用構造的高階保能量格式數值模擬方程孤立波的演化并分析格式的相對能量誤差變化.數值結果表明：高階保能量格式可以精確地模擬非線性四階薛定諤方程孤立波的實部和虛部的運動，同時，能精確地保持方程的的離散能量守恒特性.在保非線性四階薛定諤方程的能量守恒特性方面，文中的格式具有優越性.

[1] KONG Linghua,HONG Jialin,WANG Lan.Symplectic integrator for nonlinear high order Schr?dinger equation with a trapped term[J].Journal of Computation and Applied Mathematics,2009,231(2):664-679.

[2] 黃浪揚.非線性四階薛定諤方程的半顯式多辛擬譜格式[J].華僑大學學報(自然科學版),2013,34(6):706-709.

[3] GONG Yuezheng,CAI Jiaxiang,WANG Yushun.Some new strure-preserving algorithms for general muti-symplectic formulations of Hamiltonian PDEs[J].Journal of Computational Physics,2014,279:80-102.

[4] CELLEDONI E,GRIMM V,MCLAREN D I,etal.Preserving energy resp.dissipation in numerical PDEs using the "average vector filed" method[J].Communications of Computational Physics,2012,231(20):6770-6789.

[5] 蔣朝龍,黃榮芳,孫建強.耦合非線性薛定諤方程的平均離散梯度法[J].工程數學學報,2014,31(5):707-718.

[6] QUISPEL G R W,MCLAREN D I.A new class of energy-preserving numerical integration methods[J].Journal of Physics A Mathematical and Theoretical,2008,41(4):045206(1-7).

[7] KARPMAN V I.Stabilization of soliton instabilities by higher-order dispersion:Fourth order nonlinear Schr?dinger-type equations[J].Physical Review E,1996(53):1336-1339.

[8] KARPMAN V I,SHAGALOV A G.Stability of soliton described by nonlinear equation Schr?dinger-type with higher-order disperion[J].Physical D: Nonlinear Phenomena,2000(144):194-210.

[9] PAUSADER B.The cubic fourth-order Schr?dinger equation[J].Journal of Functional Analysis, 2009, 256(8):2473-2517.

[10] HONG Jialin,KONG Linghua.Novel multi-symplectic integrators for nonlinear fourth-order Schr?dinger equation with trapped term[J].Communications in Computational Physics,2010,7(3):613-630.

[11] CHEN Jingbo,QIN Mengzhao.Multi-symplectic Fourier pseudospectral method for the nonlinear Schr?dinger equation[J].Electronic Trasactions on Numerical Analysis Publisher,2001,12(11):193-204.

(責任編輯： 錢筠英文審校： 黃心中)

HighOrderEnergyPreservingMethodforNonlinearFourth-OrderSchr?dingerEquation

WANG Yifan, SUN Jianqiang, CHEN Xiaowei

(College of Information Science and Technology, Hainan University, Haikou 570228, China)

10.11830/ISSN.1000-5013.201611037

2016-11-12

孫建強(1971-)，男，教授，博士，主要從事微分方程數值解法的研究.E-mail:sunjq123@qq.com.

國家自然科學基金資助項目(11561018)； 海南省自然科學基金資助項目(114003).

O 241.5

A

1000-5013(2017)05-0742-05