物流配送問題中貪心算法與動態規劃法的分析與應用

徐西嘯

摘要計算機的應用觸及到了生活的各個方面，它的優點之一就在于強大的計算處理能力上，這也正是物流領域配送路線的問題所需要的。如何選擇最佳路線，如何節約物流運輸成本，即選擇配送的最短路線，我們可以通過貪心算法和動態規劃算法來做決定。本文對于中國現今發展蓬勃的電子商務的線下運輸問題提出了見解，以一個簡化的模型介紹了貪心算法以及動態規劃法的應用，為線下運輸問題提出了解決方案，有著十分重要的現實意義。

關鍵詞物流問題；最短路徑；最小時間；貪心算法；動態規劃

計算機自誕生以來，發展迅速，在社會中的各個領域都得到了廣泛的應用。使用計算機快速處理問題成為當今社會發展的需要。筆者運用計算機知識為現實問題提供一些意見和建議。筆者在今年“雙十一”期間親身經歷了爆倉問題，發現物體配送效率低下，“雙十一”期間物流速度極慢，形式十分嚴峻。據官方所提供的數據，買家每秒創建訂單數額達到17.5萬筆，有些貨物甚至預計需要1個月左右的時間才能配送完畢。

對于現今的物流配送，人們大多選擇第三方物流。當貨物運送到某地區時，物流公司的將貨物囤積在一處，再通過快遞員將快遞送往千家萬戶。筆者在此希望對快遞員的派送路線進行合理化選擇，以最短路程，最小時間完成貨物的配送。

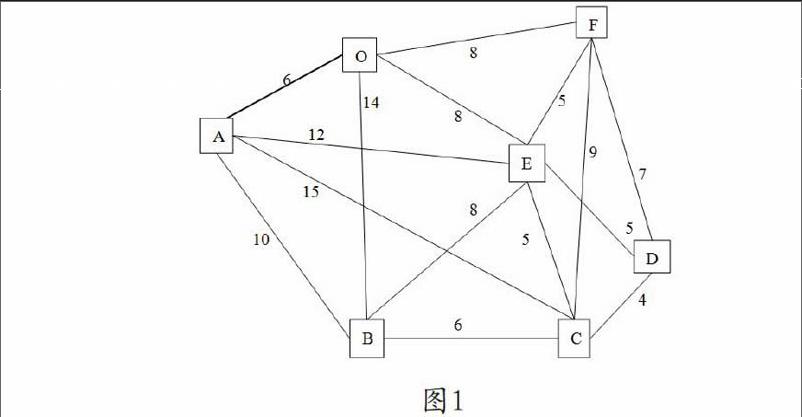
以城市中的快遞配送為例，現簡化模型如下：快遞員在某地區配送快遞，快遞公司（貨物囤積地）位于0點，快遞員需要派送6份快遞，分別送往A，B，C，D，E，F六個地點，每兩個地點之間的距離已標出，快遞員如何快速規劃路線，以最短路徑、最小時間完成快遞的配送，這不僅可以節約勞動力提高工作效率，也會使網購用戶收貨速度更快。

在具體代碼實現中配送需求地映射為編號：0-0，A-1，B-2，C-3，D-4，E-5，F-6：

城市之間的距離用二維數組來表示，記為D[i][j]，如：D[0][1]表示0與A之間的距離，于是D[0][1]=6；設置flag[][]，初始為0，表示此變量未被訪問（配送需求地未到達過），若被訪問（已到達過配送完畢）則修改為1。

本文中筆者選擇貪心算法、動態規劃法來解決這一實際問題。

1貪心算法

貪心算法（Greedy algorithm）是一種對某些動態規劃中求優秀解的簡單、迅速的算法，以當前情況為基礎根據某個標準作最優選擇，而不考慮整體情況，省去大量時間。

貪心算法在解決問題的策略上缺點是目光短淺，只根據當前已有的信息就做出選擇，而且一旦做出了選擇，不管將來有什么結果，這個選擇都不會改變。換言之，貪心算法并不是從整體最優考慮，它所做出的選擇只是在某種意義上的局部最優。這種局部最優選擇并不總能獲得整體最優解，但通常能獲得近似最優解。但由于其處理問題簡單高效、節省空間，非常適合實際問題的解決。

現在我們通過來解決這一問題，采用最近鄰點策略：從某地點（初始為快遞公司，即0點）出發，每次在沒有到過的中選擇距離當前所在地中最近的一個，直到經過了所有的配送需求地，完成了所有配送任務，最后回到快遞公司，即0點。

貪心算法具體求解流程如下：1）了解要求送達地點的的數量與各地點之間的距離。2）重復以下兩步直至已全部送達：（1）循環遍歷找到與當前出發地點最近的未到達過的配送需求地；（2）以當前找到的（最近一次找到的）送達地點為出發地點，重復步驟（1）。3）回到出發地點。

在本題中貪心算法選擇路線經過如下：快遞員從0點選擇較近的A點作為目的地。到達后選擇距離當前出發點A較近的點，0點當前已訪問，選擇B點。而后依次按照此規則選擇配送需求點，當所有快遞配送完畢返回0點，即快遞公司所在地。路線為0->AV>B->C->D>E->F->0。路程為44。

從本例中也可以看出，貪心算法簡單便捷，對于問題的解決有很大的幫助。同時我們清楚地看出，使用貪心算法只能考慮當前的選擇，當面對復雜的整體問題時，貪心算法未必能給出最優解只求出了近似最優解。

2動態規劃算法

動態規劃算法通常用于求解具有某種最優性質的問題。在這類問題中，可能會有許多可行解。每一個解都對應于一個值，我們希望找到具有最優值的解。如本問題的簡化模型有許多可以把貨物送達的可行解，但我們希望找到能實現最短路程最小時間的最優解。

動態規劃算法與分治法類似，其基本思想也是將待求解問題分解成若干個子問題，先求解子問題，然后從這些子問題的解得到原問題的解。與分治法不同的是，適合于用動態規劃求解的問題，經分解得到子問題往往不是互相獨立的。若用分治法來解這類問題，則分解得到的子問題數目太多，有些子問題被重復計算了很多次。

如果我們能夠保存已解決的子問題的答案，而在需要時再找出已求得的答案，這樣就可以避免大量的重復計算，節省時間。我們可以用一個表來記錄所有已解的子問題的答案。不管該子問題以后是否被用到，只要它被計算過，就將其結果填入表中。

在利用動態規劃求解的過程中值得注意的就是是否包含最優子結構，簡單來講就是一個問題的最優解是不是包含著子問題的最優解。利用求解子問題的最優解最后得到整個問題的最優解，這是利用動態規劃求解問題的基本前提。

動態規劃的求解過程主要分為如下的四步：1）描述最優解的結構；2）遞歸定義最優解的值；3）按白底向上的方式計算最優解的值；4）由計算出的結果構造一個最優解。

在本快遞配送問題的簡單模型中求解過程具體如下：假設從頂點0出發，令stM表示從頂點0出發經過圖中各個頂點，即配送需求地一次且僅一次最后回到出發點的最短路徑長度。

2.1描述最優解的結構

要使得從0（以0表示出發處0節點）點出發配送完畢回到0（以7表示返回處0節點，D[7][k]=D[0][k]）點的路程最短，令f（i）為到第i個節點的最短距離，則f（7）=min{D[7][1]，D17][5]，D[7][6]），用同樣的方法可以求得f（1），f（5），f（6）等。

2.2遞歸定義最優解的值

f（i）=min（f（j）+D[i][j]），其中j表示與i邊有連接的節點。

2.3按自底向上的方式計算每個節點的最優值

此時我們就得利用遞歸公式分別求解f（0），f（1），f（2）…f（7），這樣最終便能得到最終的解。

2.4由計算出的結果構造一個最優解

本模型最終解為路線為0-（0）>A（1）->B（2）->c（3）->D（4）->E（5）->F（6）->0（7）。路程為44。

動態規劃算法關鍵在于解決了重復計算的問題，大大提高了代碼運行效率。總體來說，動態規劃算法就是一系列以空間換取時間的算法。

3結論

中國電商業發展十分迅速，但長期以來，線下運輸物流配送速度為人所詬病，筆者認為應該有著更高效的配送方式。本文主要利用貪心算法和動態規劃算法來進行求解，快速而準確地得出流配送的近似最佳或最佳路線選擇，節約物流運輸成本，提高消費者滿意度，對快遞公司派發快遞的路線考慮有很強的現實參考意義。endprint