基于混沌遺傳算子的人工魚群算法①

樊友洪, 鄧 韌, 李生林, 羅凱文, 郭宇棟

?

基于混沌遺傳算子的人工魚群算法①

樊友洪, 鄧 韌, 李生林, 羅凱文, 郭宇棟

(中國人民解放軍后勤工程學(xué)院, 重慶 401331)

為提高人工魚群算法的計算精度和收斂速度, 在全局版人工魚群算法的基礎(chǔ)上, 利用混沌遺傳算子, 增加魚群迭代的混沌擾動以避免局部極值陷阱的同時較大提高了魚群整體的優(yōu)化效果和計算精度, 加快了算法收斂速度. 仿真結(jié)果表明, 該算法有效可行.

人工魚群; 混沌; 遺傳算法

人工魚群算法是由李曉磊[1]等人提出的一種群智能隨機(jī)全局優(yōu)化技術(shù), 它模擬自然界中魚的集群游弋覓食行為, 通過群魚相互間的自治協(xié)作完成全局尋優(yōu)的過程, 具有算法簡單易實現(xiàn), 可全局尋優(yōu), 并具有初值不敏感, 魯棒性強(qiáng)的特點. 但AFSA 算法搜索效率較低, 原因有: 一是人工魚群可視域的限制使算法易于進(jìn)入局部陷阱; 二是當(dāng)尋優(yōu)的區(qū)域較大或處于變化平坦的區(qū)域時收斂于全局最優(yōu)解的速度減慢、搜索性能劣化, 甚至?xí)萑刖植孔顑?yōu); 三是算法一般在優(yōu)化初期收斂快, 后期因步長等原因收斂往往較慢, 有時求解精度不高[2,3]. 本文提出一種基于混沌遺傳算子的人工魚群算法來提高收斂速度和計算精度.

1　基本人工魚群算法精度與效率

AFSA中, 算法精度和算法效率是一對矛盾體, 其關(guān)鍵在于人工魚的視野和步長的設(shè)定. 基本人工魚群算法中, 人工魚的視野和步長是固定值, 如果視野和步長設(shè)定較大, 算法全局搜索能力強(qiáng)并能快速收斂, 但在收斂后期則會出現(xiàn)人工魚在最優(yōu)值附近來回振蕩的現(xiàn)象; 如果視野和步長設(shè)定較小, 算法收斂速度慢, 雖然可以提高收斂精度, 但在多峰極值的情況下, 很容易陷入局部極值而難以獲得真正的最優(yōu)解[4]. 為此, 一些研究學(xué)者針對這些缺陷做出了改進(jìn), 如張梅鳳[5]等提出了基于生境的人工魚群算法, 較好解決了多峰問題, 但步驟比較繁瑣; 劉彥君[6]、許恒迎[7]等通過自適應(yīng)地改變?nèi)斯~的視野和步長提高了尋優(yōu)精度, 但是易陷入局部極值; 王聯(lián)國[8]提出了全局版人工魚群算法, 提高了運算速度, 但目標(biāo)的尋優(yōu)精度有待提高; 祁俊[9]等提出基于雙混沌映射改進(jìn)的人工魚群算法, 利用混沌搜索的遍歷性和初值敏感性, 使得陷入局部極值的人工魚群跳出陷阱, 但運算速度較慢; M Tuba[10]等嘗試?yán)枚嗑€程技術(shù)提高人工魚群算法精度, 但多線程協(xié)調(diào)和任務(wù)分配增加了算法的復(fù)雜度; Y. Y. Wang[11]等將人工魚群算法與群搜索優(yōu)化算法結(jié)合, 提高了尋優(yōu)精度, 但收斂速度有待提高.

本文在這些學(xué)者的研究成果之上, 結(jié)合混沌遺傳算子和自適應(yīng)視野步長改變算法, 提出一種基于混沌遺傳算子的人工魚群算法(Chaotic Genetic Artificial Fish Swarm Algorithm——CGAFSA)來提高收斂速度和計算精度. 該算法一方面結(jié)合遺傳算法, 保留和繁殖人工魚群中優(yōu)秀的人工魚, 使得最終整個魚群的優(yōu)良率得到大幅提高; 另一方面采用混沌算法提高人工魚群初始化的均布性和遺傳變異的隨機(jī)性, 可以增強(qiáng)算法全局尋優(yōu)的能力.

2　基于混沌遺傳算子的人工魚群算法

2.1混沌遺傳算子

混沌遺傳算子是遺傳算法中加入混沌變量進(jìn)行變異以獲取子代的算子, 本文在基本人工魚群算法的基礎(chǔ)上引入遺傳算法和混沌遺傳算子, 目的是在不影響收斂性的基礎(chǔ)上, 增加魚群迭代的混沌擾動, 盡量避免局部極值陷阱, 加快尋優(yōu)速度.

2.2基于混沌遺傳算子的人工魚行為描述

2.2.1混沌初始化行為

基本人工魚群算法雖然具有初值不敏感, 魯棒性強(qiáng)的特點, 但是如果人工魚群初始化盡量的均勻化的分布在可能的解空間, 可以有效地提高尋找最優(yōu)解的效率. 利用混沌算法的遍歷性產(chǎn)生分布均勻的人工魚群, 可以得到質(zhì)量較好的初始解群, 較大提高人工魚群尋優(yōu)的計算效率. 本文采用Tent映射產(chǎn)生初始的人工魚群, 其映射方程為:

2.2.2聚群行為

2.2.3追尾行為

2.2.4覓食行為

2.2.5遺傳行為

基本人工魚群算法并不模擬魚群的生態(tài)遺傳行為, 但生物遺傳是物競天擇、適者生存的重要因素, 遺傳算法在最優(yōu)化問題上的廣泛應(yīng)用說明遺傳行為的獨特性和可行性; 因此本文納入遺傳算子等來模擬魚群的遺傳行為. 設(shè),為人工魚群遺傳迭代次數(shù),為第代人工魚群總體食物濃度,為第代人工魚群平均食物濃度, 第代人工魚單體獲取食物濃度水平為. 第代人工魚群以單體獲取食物濃度水平高的前條人工魚復(fù)制產(chǎn)生其子代, 用以進(jìn)行聚群和追尾等行為.的計算方式, 最大化問題時如式(6):

最小化問題時如式(7):

2.2.6變異行為

生物基因的變異行為是造就生物多樣性的重要因素, 人工魚群利用變異行為可以對尋優(yōu)過程實施擾動, 可以更好地逃離局部最優(yōu)解, 達(dá)到全局尋優(yōu)的目的. 第代人工魚群, 對于單體獲取食物濃度水平較低的后條人工魚, 利用混沌變異算子獲取子代.的計算方式, 最大化問題時如式(8):

最小化問題時如式(9):

混沌變異算子如式(10):

2.2.7對人工魚群視野和步長的改變

根據(jù)文獻(xiàn)[12]方法對人工魚的視野和步長進(jìn)行調(diào)整:

2.2.8公告板

算法中定義了公告板, 用來記錄最優(yōu)人工魚個體的狀態(tài). 每條人工魚在尋優(yōu)過程中, 行動完畢將自身的當(dāng)前狀態(tài)與公告板的狀態(tài)進(jìn)行比較, 如果優(yōu)于公告板狀態(tài), 就用自身狀態(tài)更新公告板的狀態(tài), 否則公告板的狀態(tài)保持不變, 這樣當(dāng)整個算法迭代結(jié)束后, 公告板中記錄的狀態(tài)就是最優(yōu)個體的狀態(tài).

2.2.9算法流程

Step2: 利用Tent映射混沌初始化人工魚群;

Step3: 計算人工魚個體食物濃度, 以最優(yōu)個體狀態(tài)更新公告板;

Step5: 計算人工魚群總體食物濃度, 平均食物濃度水平及人工魚個體食物濃度水平并排序;

3　仿真試驗及分析

本文實驗環(huán)境為Windows 7, Matlab R, 6.55a, 實驗硬件平臺采用Intel Core2 CPU, 主頻為2.10GHz, 內(nèi)存2GB. 選用三個經(jīng)典測試函數(shù)進(jìn)行實驗:

Square Sum Function:

Rastrigin Function:

Griewank Function:

本文主要采用文獻(xiàn)[4]中的GAFSA和CGAFSA兩種算法進(jìn)行對比實驗.

3.1參數(shù)給定

3.2 實驗結(jié)果

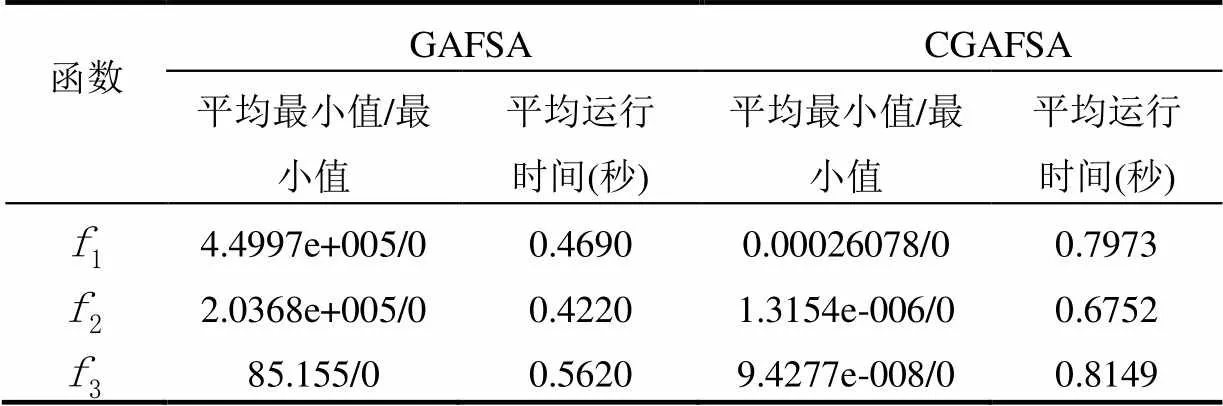
表1 兩種優(yōu)化算法計算結(jié)果

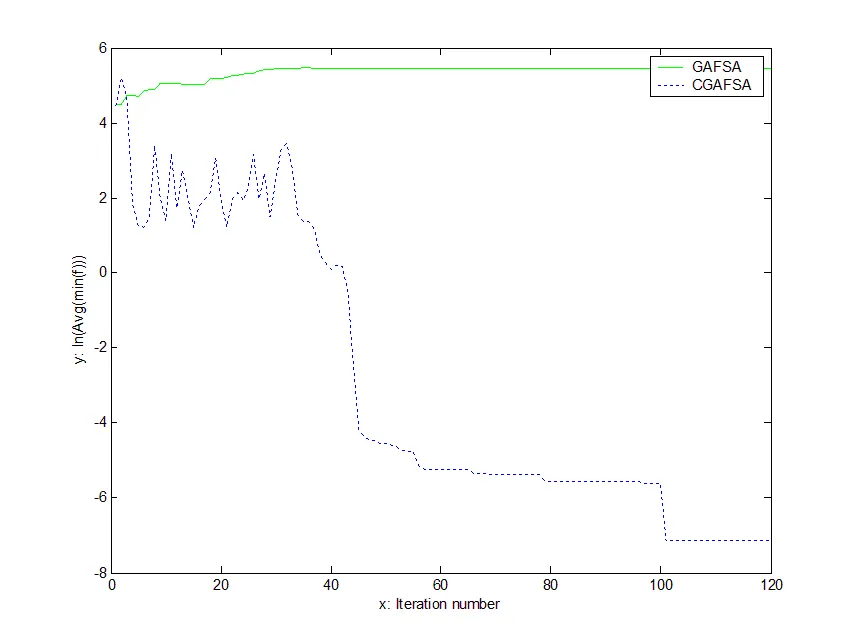
圖1 函數(shù)平均最小值的進(jìn)化曲線

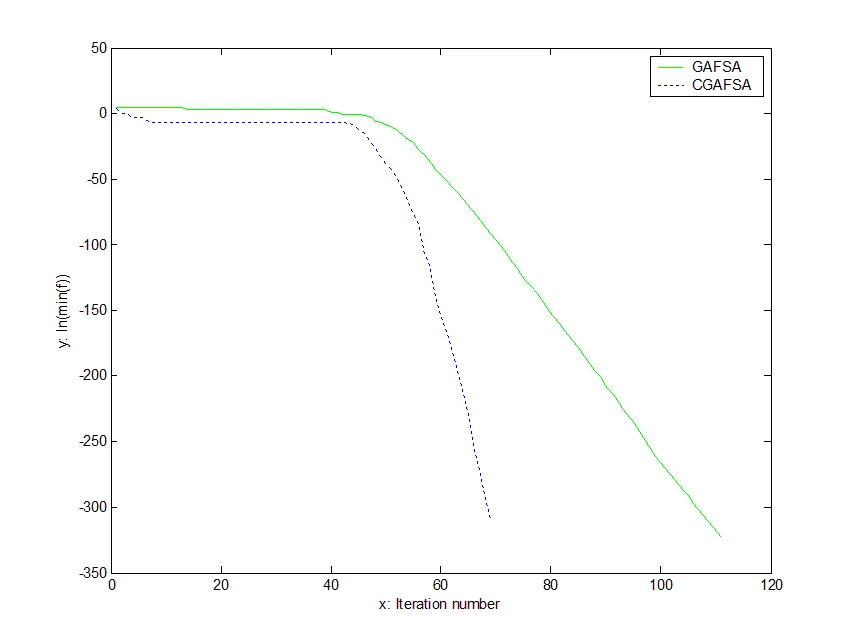
圖2 函數(shù)最小值的進(jìn)化曲線

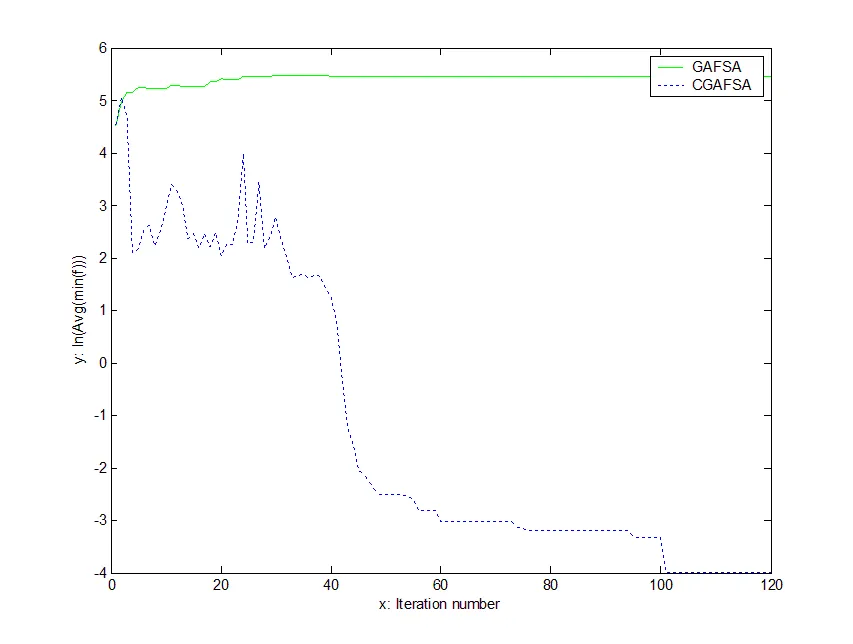
圖3 函數(shù)平均最小值的進(jìn)化曲線

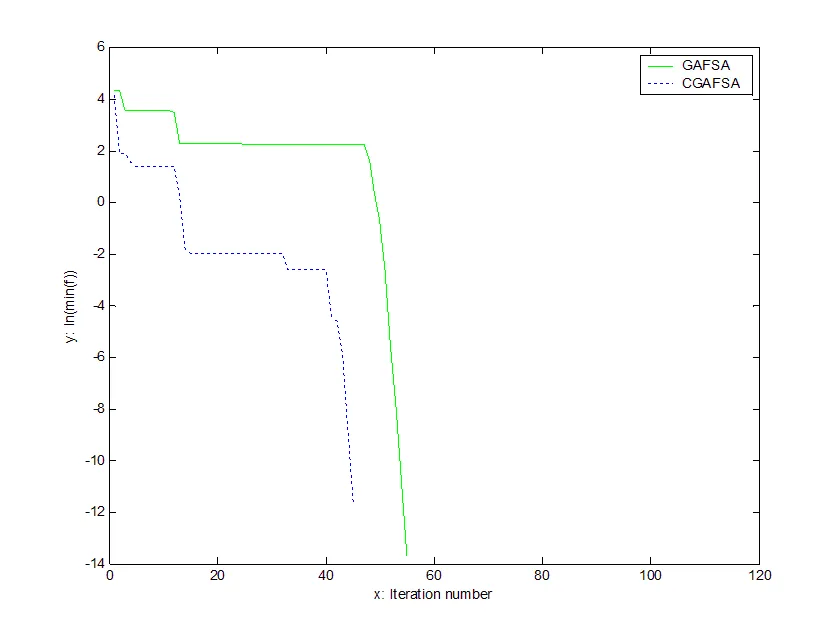
圖4 函數(shù)最小值的進(jìn)化曲線

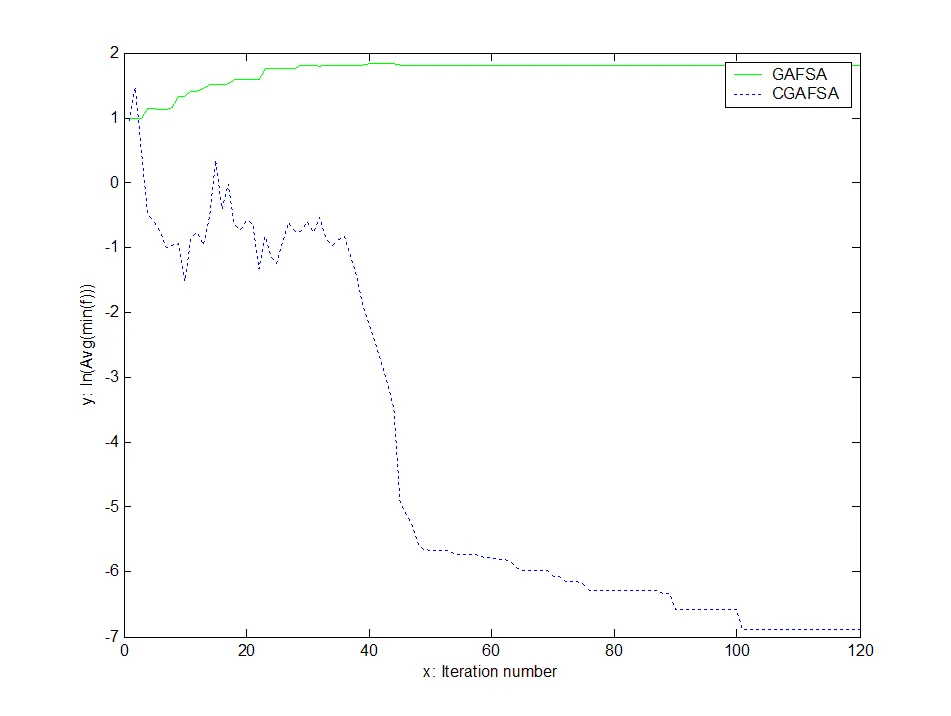
圖5 函數(shù)平均最小值的進(jìn)化曲線

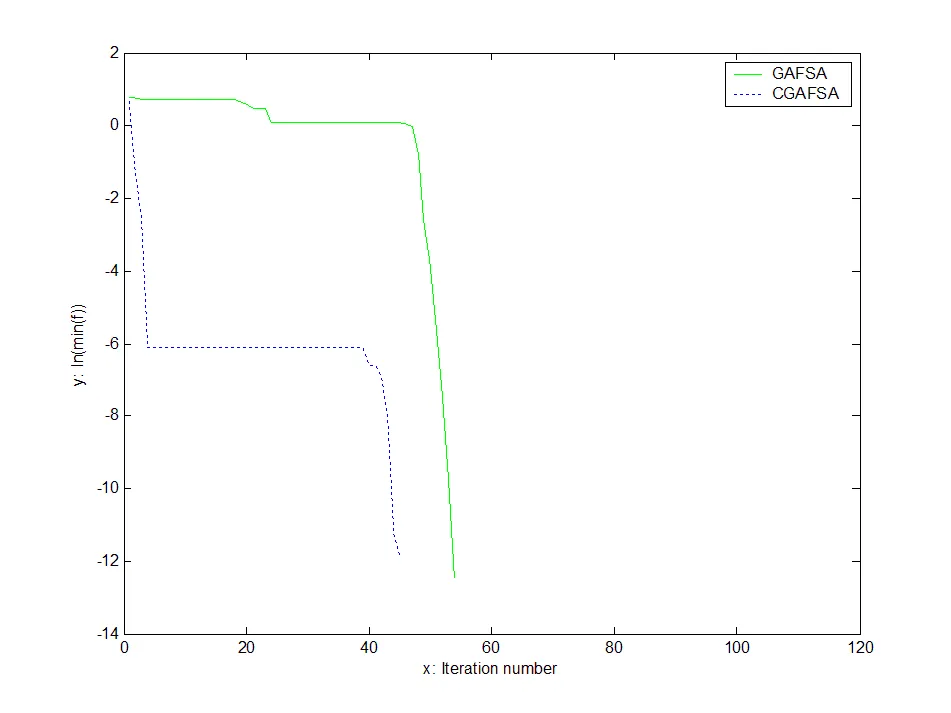
圖6 函數(shù)最小值的進(jìn)化曲線

4　結(jié)語

為提高人工魚群算法的計算精度和收斂速度, 本文在全局版人工魚群算法的基礎(chǔ)上, 利用混沌遺傳算子, 增加魚群迭代的混沌擾動, 盡量避免局部極值陷阱; 并利用遺傳算法的尋優(yōu)特性, 極大提高了魚群整體的優(yōu)化效果和計算精度, 加快了算法收斂速度. 仿真結(jié)果表明, 該算法有效可行.

1 李曉磊,邵之江,錢積薪.一種基于動物自治體的尋優(yōu)模式:魚群算法.系統(tǒng)工程理論與實踐,2002,22(11):32–38.

2 Cai Y. Artificial fish school algorithm applied in a combinatorial optimization problem. Intelligent Systems and Applications, 2010, 2(1): 37–43.

3 Zhou YQ, Xie ZC. Improved artificial fish-school swarm algorithm for solving TSP. Systems Engineering and Electronics, 2009, 31: 1458–1461.

4 王聯(lián)國,施秋紅.人工魚群算法的參數(shù)分析.計算機(jī)工程, 2010,36(24):169–171.

5 王聯(lián)國,洪毅,施秋紅.全局版人工魚群算法.系統(tǒng)仿真學(xué)報, 2009,21(23):7483–7486.

6 張梅鳳,邵誠.多峰函數(shù)優(yōu)化的生境人工魚群算法.控制理論與應(yīng)用,2008,4(25):773–776.

7 劉彥君,江銘炎.自適應(yīng)視野和步長的改進(jìn)人工魚群算法.計算機(jī)工程與應(yīng)用,2009,45(25):35–37.

8 許恒迎,孫偉斌,張霞,等.自適應(yīng)視野和步長的局部領(lǐng)域人工魚群算法.計算機(jī)工程與設(shè)計,2012,33(7):2815–2820.

9 祁俊,趙慧雅,李明.基于雙混沌映射改進(jìn)的人工魚群算法.計算機(jī)應(yīng)用與軟件,2012,29(9):230–233.

10 Tuba M, Bacanin N, Stanarevic N. Multithreaded implementation and performance of a modified artificial fish swarm algorithm for unconstrained optimization. International Journal of Mathematics & Computers in Simulation, 2013, 7(3): 215–222.

11 Wang YY, Li LJ. An improved intelligent algorithm based on the group search algorithm and the artificial fish swarm algorithm. Int. J. Optim. Civil Eng., 2015, 5(1): 37–52.

12 王聯(lián)國,洪毅,趙付青,等.基于鄰域正交交叉算子的人工魚群算法.農(nóng)業(yè)機(jī)械學(xué)報,2008,39(8):140–144.

Artificial Fish Swarm Algorithm Based on Chaotic Genetic Operation

FAN You-Hong, DENG Ren, LI Sheng-Lin, LUO Kai-Wen, GUO Yu-Dong

(Logistic Engineering University of PLA, Chongqing 401331, China)

A novel algorithm based on chaotic genetic operation is presented in this article to improve computation precision and convergence rate of original artificial fish swarm algorithm. With the chaotic disturbance increasing in fish swarm genetic iteration, the trap of local extremum is avoided, while the optimization effect, computation precision and convergence rate are also improved. Simulation result shows it works well and plays the specialties of genetic algorithm and fish swam algorithm.

artificial fish swarm algorithm; chaos; genetic algorithm

2016-06-22;

2016-08-08

[10.15888/j.cnki.csa.005664]