單線圖動態規劃最優布局成圖技術①

趙 越, 李 培, 王 震, 王 平

?

單線圖動態規劃最優布局成圖技術①

趙 越1, 李 培1, 王 震2, 王 平2

1(國網江蘇省電力公司揚州供電公司, 揚州225000)2(廈門億力吉奧信息科技有限公司, 廈門361008)

提出了一種基于動態規劃算法得到布局最優解實現區域電網單線圖生成的方法. 根據電網空間數據構建拓撲模型, 執行廣度優先算法得到多個能構成連通圖的鄰接矩陣以及矩陣遍歷序列, 根據鄰接矩陣寬度計算出能容納全部設備的正方形范圍, 并建立了設備最小間距為優化目標的數學模型. 提出了動態規劃最優布局求解的算法, 應用該算法求解布局最優解數組, 最后按照最少交叉原則進行正交化處理. 應用實例表明通過最優解布局的成圖美觀且高效.

區域電網; 拓撲模型; 動態規劃算法; 單線圖; 布局最優解

單線圖對于電網的意義和價值非常大, 不管是配網生產的規劃設計、電網調度的調度管理還是配網運行的運行檢修, 單線圖都是一種必不可少的常用工具. 不過隨著電網建設更新日新月異, 單線圖更新也日益頻繁, 同時電網用戶對于單線圖的展現效果要求亦不斷提高, 因此單線圖的維護工作量越來越多, 如果能有一種可行、高效、美觀的單線圖自動生成方法來解決這個難題, 就可以進一步提高配網生產的工作效率.

當前國內許多學者針對電網地理信息到單線圖的自動生成課題進行了大量研究[1-3]. 同時國內外還有很多學者對于退火算法、樹圖算法、遺傳算法等各種先進算法在單線圖布線上的結合應用也進行了研究和實踐[4-13]. 以上文獻提出的單線圖自動生成方法都有一定的參考價值, 但是無法滿足目前日益復雜的電網結構以及用戶不斷提高的布局展示要求.

如何設計合適算法, 結合電力GIS系統準確高效的實現單線圖的自動生成, 值得進行深入研究, 本文在深入了解電網單線圖自動生成具體要求以及綜合各種先進布局理論算法后, 提出了運用動態規劃算法分階段計算并最終得到符合電網生產實際使用所需單線圖自動生成的方法.

1 基于動態規劃算法的圖形布局機制

目前行業內存在各種專題圖系統, 其中圖形布局所采用的算法基本上為以下三種算法.

a) 樹圖布局算法: 層次數據的空間填充性布局算法;

缺點: 應對復雜層次數據時, 有序樹圖正方化性能差, 難以滿足各層數據展現需求, 需要人工參與.

b) 正交遺傳算法: 通過旋轉正交法快速提取解空間中的優異個體的布局算法;

缺點: 算法對新空間的探索能力是有限的, 也容易收斂到局部最優解. 涉及到大量個體的計算, 當問題復雜時, 嚴重影響性能, 同時對非線性約束的處理方式是添加懲罰因子, 這是一筆不小的性能開支.

c) 有向無環算法: 采用消環、分層、排序、路徑管理的布局算法.

缺點: 很多電網數據局部成環, 無法處理.

為了避免布局時的人工參與, 減少計算性能消耗, 在通過綜合蟻群算法、褪火算法、正交遺傳算法、貪心算法、動態規劃算法等先進理論算法后, 最終在動態規劃算法的基礎上延伸拓展出最適合電力網絡的布局算法.

動態規劃算法基本思想與分治法類似, 將問題分解為N個子問題, 依次解決各子問題, 最后一個子問題就是初始問題的解. 在實際應用中動態規劃算法可按以下幾個簡化的步驟進行設計:

(1) 分析最優解的性質, 并刻畫其結構特征;

(2) 遞歸的定義最優解;

(3) 以自底向上或自頂向下的記憶化方式(備忘錄法)計算出最優值;

(4) 根據計算最優值時得到的信息, 構造問題的最優解.

2 單線圖自動生成技術設計思路

基于動態規劃最優布局算法的單線圖自動生成設計思路如下.

a) 根據源地理沿布數據建立電網拓撲存儲模型, 實現設備、單線圖、拓撲關系的存儲, 然后完成各段拓撲模型的去重、合并處理, 建立網絡圖拓撲模型;

b) 根據網絡圖拓撲模型, 建立連通圖得到連通圖的鄰接矩陣, 然后采用廣度優先遍歷算法遍歷鄰接矩陣頂點得到矩陣遍歷序列;

c) 開啟動態規劃算法對序列中的頂點信息求解最優值, 得到最優值數組[];

d) 遍歷最優值數組, 按照最優值坐標放置設備, 通過圖形引擎完成每一個設備的渲染繪制;

e) 以最少交叉原則完成圖紙正交化處理.

上述步驟中, 重點在a步、c步、e 步中, 即如何建立網絡圖的拓撲模型和計算網絡圖設備最優坐標. 本文的處理方法是采用動態規劃的方法結合電力接線圖特點計算得到設備布局最優值數組.

3 網絡圖拓撲模型構建

(1) 單線圖對象存儲

根據電力系統的空間數據, 按照線路進行分類存儲設備信息和拓撲關系, 即構建多線路模型, 以單條線路為標記, 分別存儲各自對應的設備信息和拓撲關系.

//單線圖對象

{

;// 設備集合

; //版本信息

;// 圖檔類型

;// 變電站名稱

; //饋線

;// 饋線名稱

;// 坐標原點

; //連接關系列表

;// 關聯關系(包含關系)

}

(2) 網絡圖對象存儲

構建基于單線圖的環網拓撲關系模型, 用于確定子圖檔與子圖檔之間的關系, 構建連通圖模型, 通過聯絡關系來確定線路之間的關系是否正常, 聯絡關系為環網點(環網開關), 拓撲關系模型包括饋線F1、饋線F2和聯絡開關K三個基本屬性.

//網絡圖對象

{

;// 版本信息

>;// 包含的子圖檔

;// 聯絡關系

}

//聯絡關系模型

{

;// 聯絡開關

1;// 饋線1的;

2;// 饋線2的

;// 與聯絡開關相連的設備

}

(3) 合并與去重復處理

對構建的各段拓撲關系模型進行合并和去重處理; 其中, 如有需要還可以簡化設備, 形成新的拓撲關系模型. 如圖 1、圖2 所示, 2 段拓撲中 A1 與A2(B1 與 B2)均代表同一個設備, 為消去相同的, 需要對兩段拓撲中的A、 B 兩個設備進行去重與合并處理, 融合成 A12、B12, 結果如圖 3 所示.

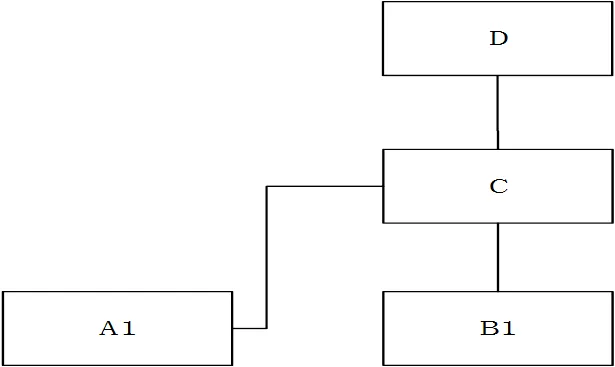
圖1 拓撲段1

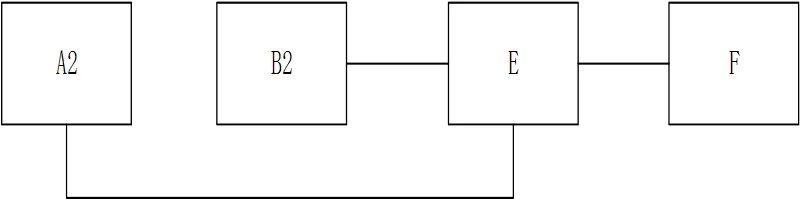
圖2 拓撲段2

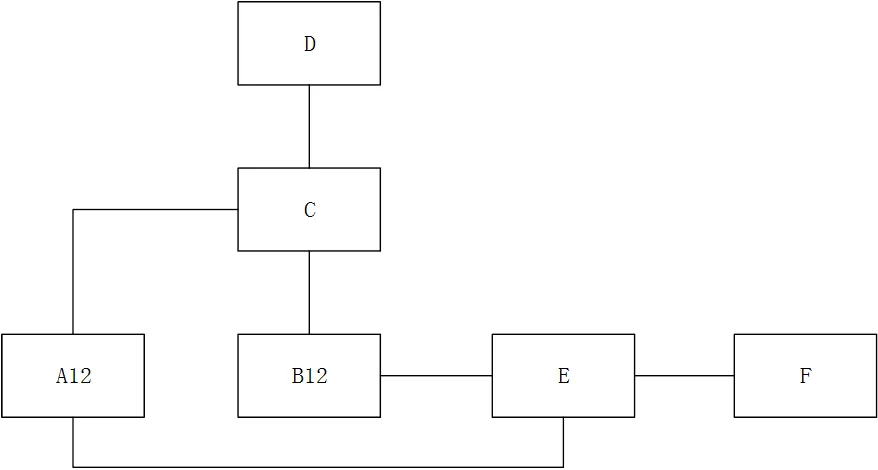
圖3 拓撲段合并處理結果

最初的線路模型經過去重與合并處理后生成了單條或者多條大的網絡拓撲模型.

4 基于動態規劃的成圖布局處理

4.1 基于動態規劃的最優值求解

(1) 獲取容納全部設備的正方形范圍

根據鄰接矩陣的寬度, 計算出一個能容納全部子圖檔并留有最少空位的正方形范圍, 考慮到范圍越大, 計算函數需要花費的時間越大, 所以使用一個能容納全部子圖檔并留有最少空位的正方形范圍;

滿足:>=(-1)*(-1);

(2) 建立設備最小間距的目標函數模型

遍歷第一個設備到最后一個設備, 如果兩個設備間有連接關系(,), 就計算兩個點之間的距離, 不重復計算距離, 為了減少設備間連接的交叉, 構建的函數模型應滿足有關系設備盡量緊湊, 同時不能重疊.

對應的函數模型為:

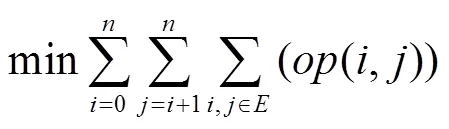
為計算設備間距離的公式:

其中,和屬于1到L之間的正整數, 代表每個備中心點的坐標值;

(3) 動態規劃算法求解最優值

開啟動態規劃算法, 迭代尋找函數新的最優解, 直到確定每個設備中心點的x和y的值.

a) 根據Link的長度(序列長度=設備數量)計算出頂點范圍, 構建*個格子, 每個格子用于存儲當前格子存儲的設備下標編號和對應的,值;

b) 根據動態規劃算法, 按下標計算出第一個設備順序放入空閑格子的函數值;

c) 根據連接關系尋找最優解并迭代執行該過程, 直至設備全部遍歷完成, 在迭代過程中需要判斷設備是否有連接, 如果無連接, 則將下標記錄到無連接數組中, 繼續迭代該過程; 否則進行動態規劃算法, 按下標繼續放置設備;

d) 遍歷完序列Link后, 整理數據, 遍歷每個子圖檔存儲的唯一格子對象, 根據格子對象中的設備對象的下標進行排序, 并返回每個設備的和值.

本算法中, 以計算解出的值是否為最小值為最優解, 即如果為最小值則記錄為最佳位置, 直至計算完畢后無法找到更小值為止. 計算完畢后, 如圖4所示, 按下標存儲每個設備的最優解, 最優解數組的格式為[](二維整形數組), 比如[1,1], [2,2], [3,3]..., [1,1]對應設備1的最佳位置.

得到最優解數組的動態規劃最優布局算法如圖4所示.

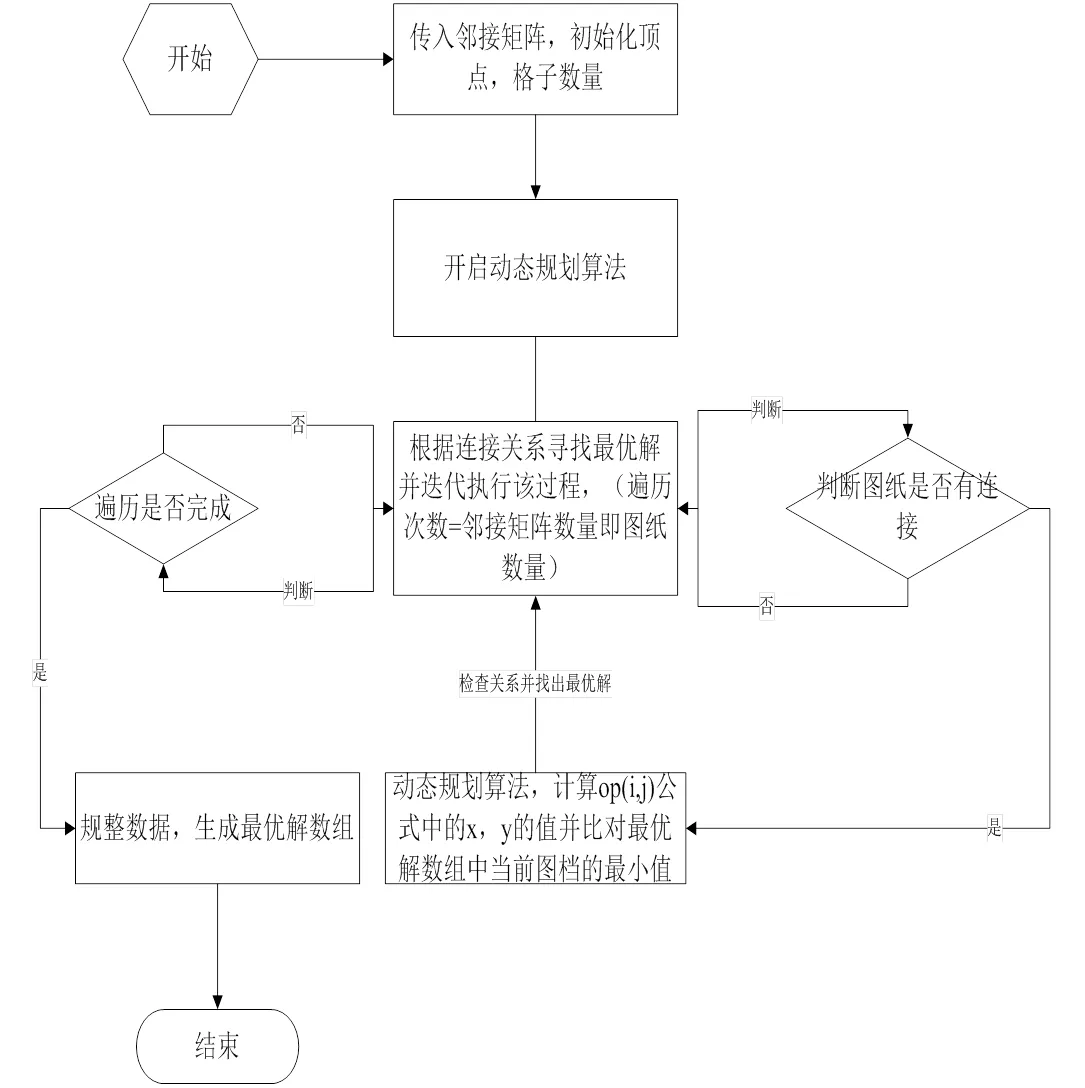
圖4 最優解數組生成流程圖

4.2 基于動態規劃的圖紙正交化處理

經過之前的處理, 每個設備都已經按層等間距互不重疊地排列, 后續的調整都不應該再調整設備的坐標, 所以我們參考設備的位置來完成圖紙正交化處理

根據單線圖基本布局規則, 所有設備之間的連線都應該是橫平豎直的, 所以需要對設備連接線按照某些規則添加一些拐點形成正交化的形態. 我們目前采用的是動態規劃的方法為邊線添加拐點達到正交化, 圖5是一幅最優布局后的圖, 我們從上到下逐層調整上下子設備之間的邊線.

以上圖為例調整上游設備與各下游設備之間連線的正交化. 首先求得上游設備連線的數目,然后求出一個中位數/2

對于每一條連線做如下處理:

(=-1;>=0;--)

{

處理左邊正交化;

+=3.0;;

}

(=;j<;++)

{

(==)

{處理中間正交化;MiddleSpace+=2.0;}

Else

{處理右邊正交化;RightSpace-=3.0;}

}

a) 處理左連線正交化

圖5 設備連線正交化處理前

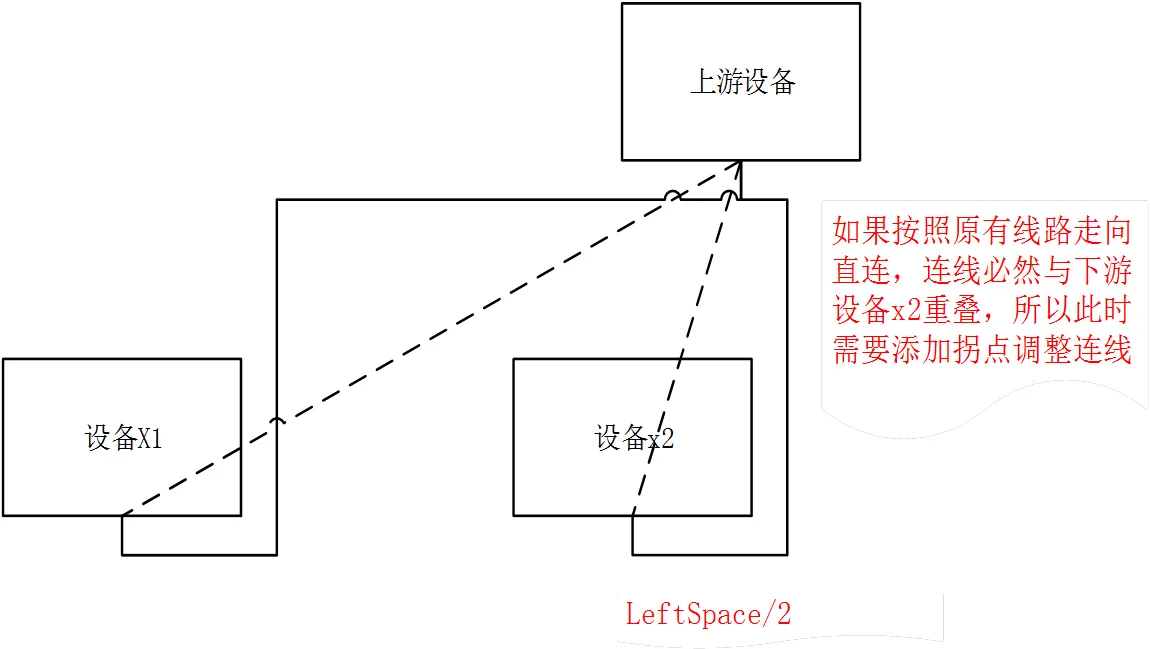
圖6 處理左連線正交化

b) 處理中間連線正交化

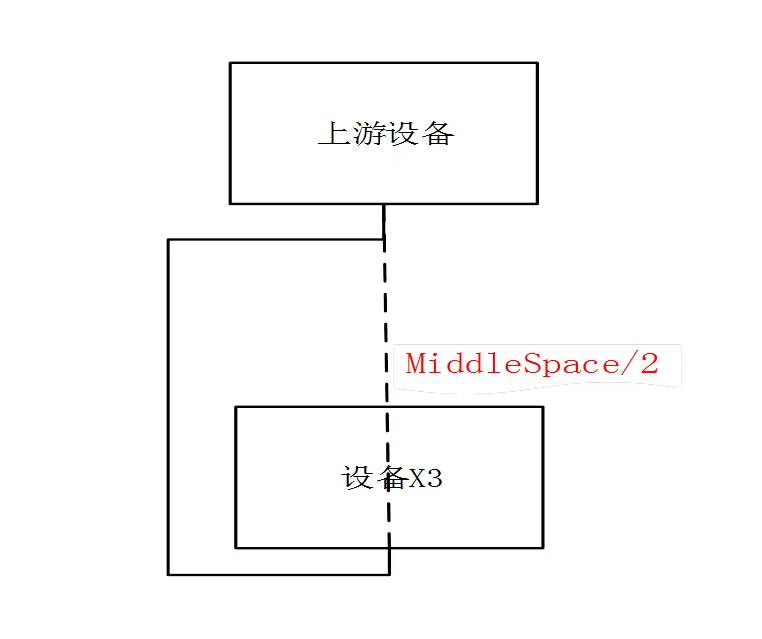
圖7 中間連線正交化

c) 處理右連線正交化

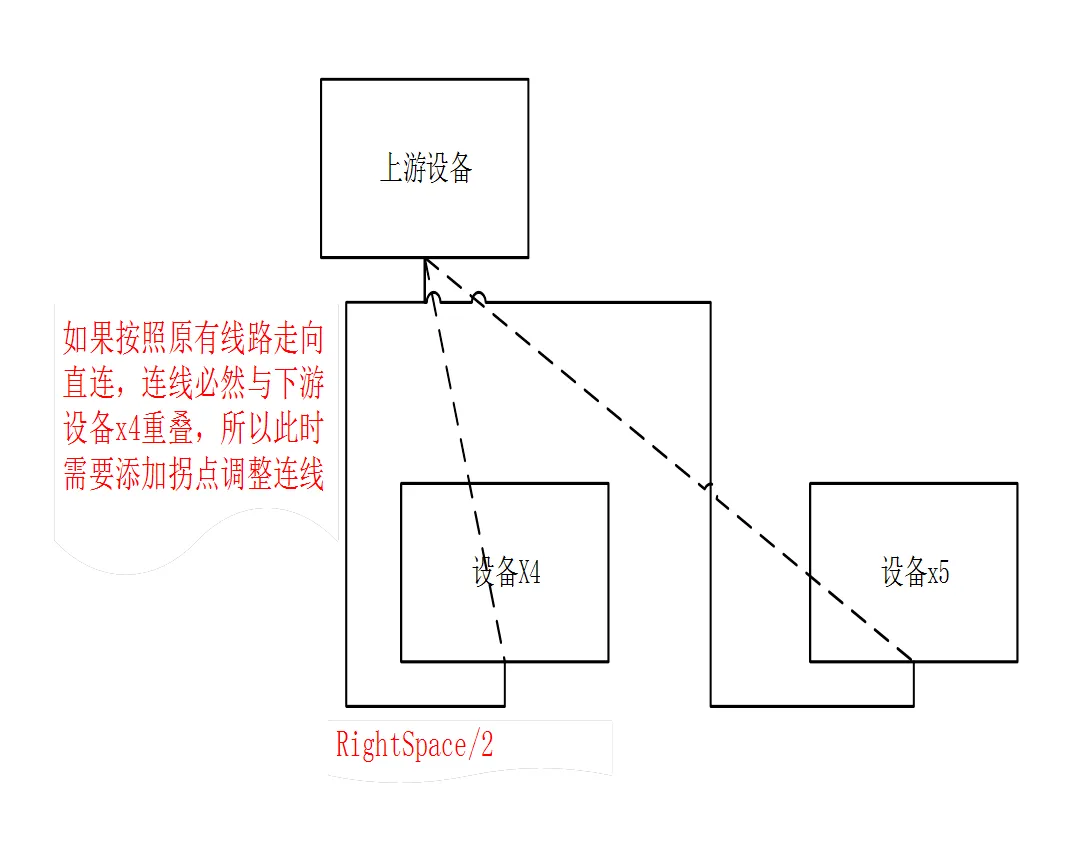
圖8 右連線正交化

以上三種處理方法都要考慮到一種情況, 如圖9, 設備X2 本身有多條線穿出, 當前調整的這條線從哪邊穿出能減少與其他邊的交叉是很值得考慮的.

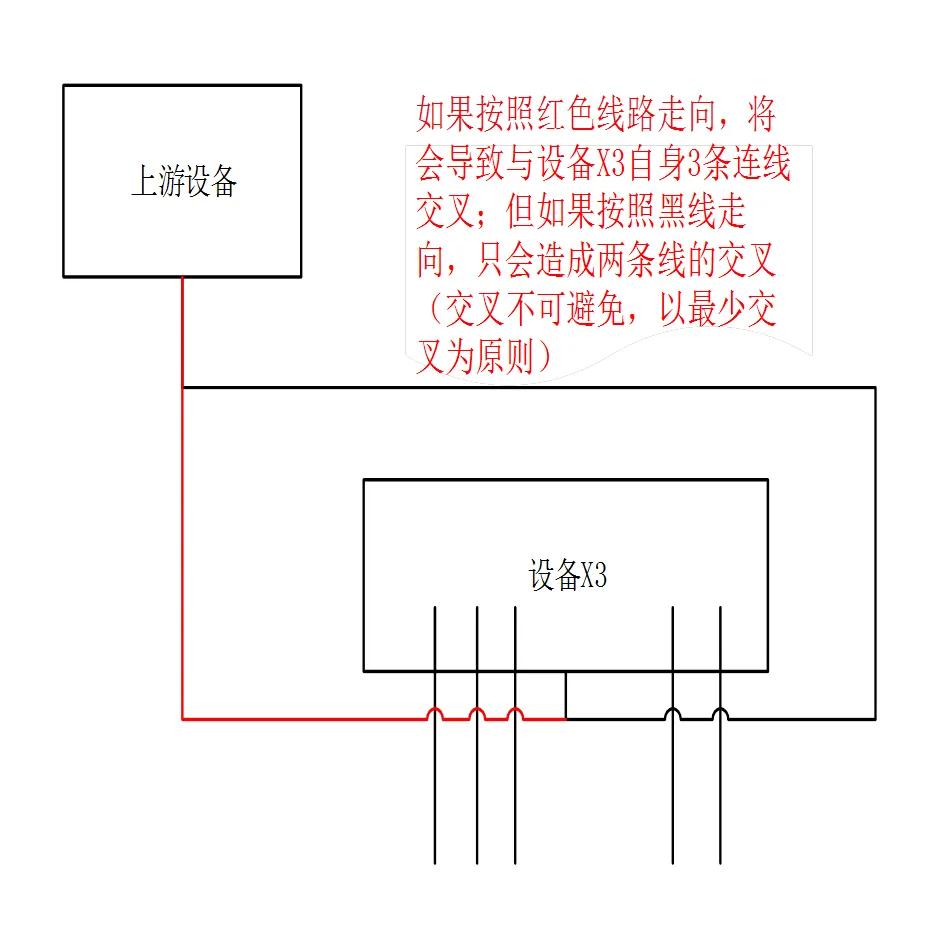
圖9 連線正交化參考下游設備調整

5 算法示例

本文引用某地區電網架構模型, 該模型具備線路之間環網多的特點, 可用于驗證上述原理. 某地區局部電網聯絡線路數據如表1所示.

表1 某地區局部電網聯絡線路數據

表中, 第1列表示聯絡開關, 第2、3、4、5列都是有聯絡關系的線路. 某地區電網采用最優布局算法前、后布局如圖9, 圖10所示. 可以看出采用動態規劃最優布局算法布局后圖形繪制區域整體布局更加均勻、美觀、清晰, 滿足單線圖自動布局的要求. 驗證了基于動態規劃方法的最優布局算法的正確性及有效性.

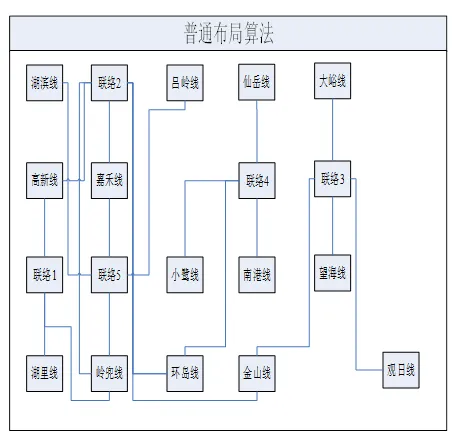
圖9 普通算法布局

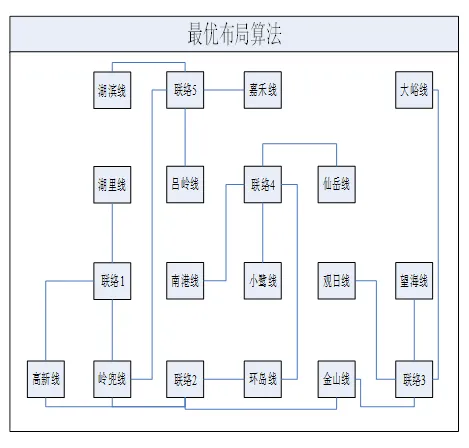
圖10 動態規劃算法布局

6 結語

本文提出了一種基于動態規劃最優布局算法的單線圖自動生成方法. 通過分析現有布局算法的不足, 并深入研究布局過程, 采用動態規劃思想重新設計布局算法, 為單線圖生成的自動布局處理提供了更多的選擇. 通過對布局算法的優化, 拓廣了動態規劃方法的應用范圍, 同時提高了單線圖自動布局的效率和美觀程度.

與現有技術相比, 存在下面兩點優點:

第一、提出了由多條線路構成的網絡連通圖構想方案, 通過函數模型計算出連通圖頂點的位置來確定設備的位置, 并且該位置是最合適的, 能夠快速、完美成圖.

第二、放棄樹圖布局算法、遺傳算法等算法, 通過算法優化, 使用動態規劃算法計算出最優解, 而不是近似的最優解.

1 徐彭亮,何光宇,梅生偉,張王俊,王偉.基于地理信息的輸電網單線圖自動生成新算法.電網技術,2008,32(21):9–12.

2 劉健,吳媛,劉鞏權.配電饋線地理圖到電氣接線圖的轉換.電力系統自動化,2005,29(14):73–77.

3 章堅民,葉琳,孫維真.基于地理相對位置的省級輸電網均勻接線圖自動生成.電力系統自動化,2010,(24):55–59.

4 陳學松,蔡述庭.基于模擬退火算法的矩形優化排樣問題的研究.數學的實踐與認識,2008,38(9):68–71.

5 沈偉,吳文傳,張伯明,鎬俊杰.能量管理系統中電網潮流單線圖自動生成算法.電力系統目動化,2010,34(6):48–53.

6 邢佳磊,楊洪耕,何亞平.地區電網運行單線圖的智能自動布局.電力系統自動化,2010,34(4):59–64.

7 王治華,董樹鋒,張王俊.輸電網單線圖自生成的新方法.電力系統保護與控制,2010,38(18):155–159.

8 張旭,馮恩民.具有性能約束布局問題的優化算法及收斂性.大連理工大學學報,2005,45(5):766–771.

9 陳勇,鄧其軍,周洪.無重疊交叉的配電網單線圖自動生成算法.電力自動化設備,2010,30(11):90–93.

10 Rossouw FJ, Beukes HJ, Enslin JHR. Modelling network problems with power flow equations and diagrams. AJ. Africon, 1999 IEEE, 1999, (2): 643–648.

11 Deng QJ, Zhou H, Chen Y. Design and implement of drawing of GOO one-line diagram of smart distribution network. 2010 International Conference Electrical and Control Engineering (ICECE). 2010. 3533–3536.

12 Li X, Feng XL, Zeng ZY, et al. Distribution feeder one-line diagrams automatic generation from geographic diagrams based on GIS. Third International Conference Electric Utility Deregulation and Restructuring and Power Technologies (DRPT 2008). 2008. 2228–2232.

13 Zhang LH, Pei XD, Kleine U. Analog macro-cell placement with very fast simulated re-annealing algorithm. Journal of Software, 2002, 13(6): 1059– 1062.

Optimal Layout Mapping Technology for Single Line Dynamic Programming

ZHAO Yue1, LI Pei1, WANG Zhen2, WANG Ping2

1(State Grid Yangzhou Power Supply Company, Yangzhou 225000, China)2(Xiamen Great Power GEO Information Technology Co. Ltd., Xiamen 361008, China)

A new method for generating the single line diagram of the regional power network is proposed based on the dynamic programming algorithm. According to the topological model of spatial data in power grid, the implementation of the breadth first algorithm can obtain the adjacency matrix and matrix traversal sequence of the connected graph, and the square range of the total equipment can be accommodated by the adjacency matrix. A dynamic programming optimal layout algorithm is proposed, which is used to solve the layout optimization problem. The application example shows that the optimal solution layout is beautiful and efficient.

regional power network; topological model; dynamic programming algorithm; single line graph; layout optimal solution

2015-11-13;

2015-12-21

[10.15888/j.cnki.csa.005256]